Устойчивое развитие: многокритериальная оценка и выбор проектов при выведении озоноразрушающих веществ из потребления

Решающая роль инновационных технологий

В контексте устойчивого развития доминирующее положение заняло мнение, что необходимо различать три составляющих основного капитала. Эти составляющие соотносятся с тремя аспектами устойчивого развития:

• •    Капитал созданный человеком (или воспроизводимый капитал). Этот капитал представляет собой общепринятую форму капитала, используемую в экономическом

анализе, и включает в себя здания, промышленное оборудование и машины, компоненты инфраструктуры и т.п.

• •    Человеческий капитал. Под человеческим капиталом понимается располагаемый человеком запас знаний, навыков, способностей и других атрибутов [6]. Его формирование, подобно накоплению физического или финансового капитала, требует отвлечения средств от текущего потребления ради получения дополнительных доходов в будущем.

• •    Природный капитал. Традиционно природный капитал рассматривался только как природные ресурсы. В настоящее время он рассматривается с более широкой позиции и включает в себя не только энергетические и минеральные ресурсы, но и все возобновляемые и некоторые квази возобновляемые ресурсы такие как, например, озоновый слой атмосферы. В широком смысле природный капитал иногда определяют как совокупность элементов экологических систем, которым можно придать экономическую ценность.

Устойчивое развитие имеет своей целью обеспечение индивидуального и общественного благосостояния. Благосостояние населения фундаментально зависит от основного капитала, приходящегося на душу населения. Для того чтобы достичь постоянного уровня потребления на душу населения в течение длительного времени, основной капитал на душу населения должен, по крайней мере, не уменьшаться в связи с ростом населения.

Однако соотношение между компонентами основного капитала может измениться. Доля природного капитала с течением времени, вероятно, будет уменьшаться. Возможность замещений между каждой парой различных компонент основного капитала принципиально ограничена и, поэтому требование обеспечения устойчивости приводит к необходимости эксплуатационной экономии. Отсюда и вытекает решающая роль инновационных технологий в достижении устойчивого развития, поскольку инновации являются основным фактором повышения уровня продуктивности. Сбережение природного капитала невозможно без инновационного развития.

Оценка и выбор проектов

Проблема вывода из потребления ОРВ в холодильной промышленности приводит к необходимости решения следующих типовых задач:

• 1.    Модификация существующего или приобретение нового оборудования, т.е. задача типа «сделать или приобрести» в секторах конечного пользования, таких как унитарные установки охлаждения и/или нагрева воздуха, чиллеры.

• 2.    Модернизация имеющегося оборудования в коммерческих секторах конечного пользования, таких как холодильные установки для коммерческого использования, теплонасосные установки, транспортные холодильные установки.

• 3.    Модернизация выпускаемой или разработка новой продукции.

• 4.    Технологическое переоборудование заводов-производителей на использование безопасных для озона технологий.

Данные задачи различаются по своей размерности, которая определяется следующими параметрами:

• •    числом альтернативных вариантов проектов;

• •    числом критериев оценки и выбора проектов.

Формирование области допустимых технических решений и набора критериев

На стадии предпроектного анализа необходимо определить набор прогрессивных технологий, т.е. область допустимых технических решений. Для этих целей наряду с другими материалами справочного характера можно воспользоваться Директивой ЕС по комплексному предотвращению и контролю загрязнения 96/61. Этот документ представляет собой систему регулирования, основанную на применении комплексного подхода к контролю и регулированию воздействий промышленных объектов на окружающую среду.

Директива определяет надлежащие схемы размещения и эксплуатации оборудования, обеспечивающие защиту и охрану окружающей среды за счет применения «наилучшей доступной техники» (Best Available Technique, сокращенно BAT). С целью оказания методической помощи проектировщикам и операторам объектов, в ЕС была осуществлена разработка ряда отраслевых справочных пособий по BAT (сокращенно BREF), которые описывают наилучшую доступную технику для каждой из отраслей промышленного производства.

Директива ЕС 96/61 не обязательна для выполнения в России, тем не менее, показатели, определенные в отраслевых справочниках по BAT, целесообразно использовать и уже иногда используются в России в качестве базовых нормативов в процессе разработки оценки воздействия на социальную ситуацию и окружающую среду для проектируемых и модернизируемых предприятий и комплексов.

При определении BAT принимается в расчет баланс между стоимостью и вредным воздействием на окружающую среду. Поэтому учет социальной составляющей устойчивого развития при выборе проекта можно обеспечить, включив в набор критериев оценки и выбора проекта соответствующие этой тематической области критерии.

Выбор методов решения задач

Задачи 1-й группы, как правило, характеризуются малой размерностью, в то время как 2-ю, 3-ю и 4-ю группы задачи отличает большая размерность.

Режимы решения задач будем различать по форме взаимодействия лица, принимающего решение (ЛПР) с рабочей группой по выбору проектов:

• •    Интерактивный: постоянное взаимодействие с ЛПР (легкий доступ к ЛПР).

• •    Итеративный: ЛПР запрашивает варианты решения проблемы и выбирает предпочтительный вариант (затруднительный доступ к ЛПР).

Начиная с шестидесятых годов прошлого столетия до настоящего времени, разработан широкий круг разнообразных подходов и методов для анализа и оптимизации многокритериальных решений.

Для выбора методов решения типовых задач вывода из потребления ОРВ были определены следующие критерии:

• •    Обоснованность. Метод должен соответствовать типу и размерности решаемой задачи. Предположения, обусловленные  методом, должны  соответствовать

реальным условиям решаемой проблемы.

• •    Когнитивность. Необходимо учитывать  общие временные  затраты ЛПР,

необходимые для применения метода. Для понимания метода должны требоваться минимальные когнитивные усилия ЛПР. Основные усилия ЛПР необходимо концентрировать на обеспечение достоверности информации, которую он предоставляет в качестве исходных данных.

• •    Эффективность. Метод должен состоять из минимального количества сложных операций, выполняемых ЛПР, для чего максимальное число сложных операций должно осуществляться ЭВМ.

• •    Проверяемость. Метод должен допускать возможность проверки достоверности информации, которую ЛПР предоставляет в качестве исходных данных.

Сравнение методов многокритериального анализа и оптимизации решений по разработанным критериям позволяет сделать вывод о целесообразности применения методов математического программирования и аналитической иерархии (АНР), разработанного

Т.Саати [7].

Поиск наилучшей альтернативы

Проиллюстрируем построение модели метода АНР для одной из задач 1-й группы[8]. В качестве примера рассмотрим решение задачи о конверсии чиллера с целью вывода из потребления ОРВ. Модификация старого чиллера, как правило, экономически не оправдана. Для сравнительно новых чиллеров целесообразно рассматривать их модификацию в качестве альтернативного варианта замене на новое оборудование. Таким образом, имеем два альтернативных проекта: проект модификации R1 и проект замены R2.

Определим критерии выбора проекта конверсии чиллера:

• •    Прямая эмиссия хладагента из-за утечки. При регулярном техническом обслуживании утечка хладагента в современных чиллерах составляет в год от 1 до 4% от общего объема. Прямую эмиссию рекомендовано измерять в эквиваленте СО 2 , используя оценки потенциала глобального потепления, изданные Межправительственной группой экспертов по изменению климата.

• •    Косвенная эмиссия. Эмиссия СО 2 , вызванная производством электроэнергии,

потребляемой чиллером.

• •    Расход воды. Общий объем всех видов воды, необходимый для функционирования чиллера.

• •    Размер инвестиции. Затраты на проект, связанные с вводом нового чиллера в эксплуатацию или с проведением модификации имеющегося оборудования.

• •    Эксплуатационные расходы.

• •    Срок службы оборудования. Оценка производителя срока службы нового чиллера или экспертная оценка срока службы оборудования, находящегося в эксплуатации.

• •    Срок окупаемости. Период времени, по истечении которого ожидается погашение инвестиции.

Модель метода АНР в виде иерархии «цель-критерии-альтернативы» будет иметь вид (рис. 4.) [8].

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление» www.rypravlenie.ru                                                             том 3 (2009), ст. 3.

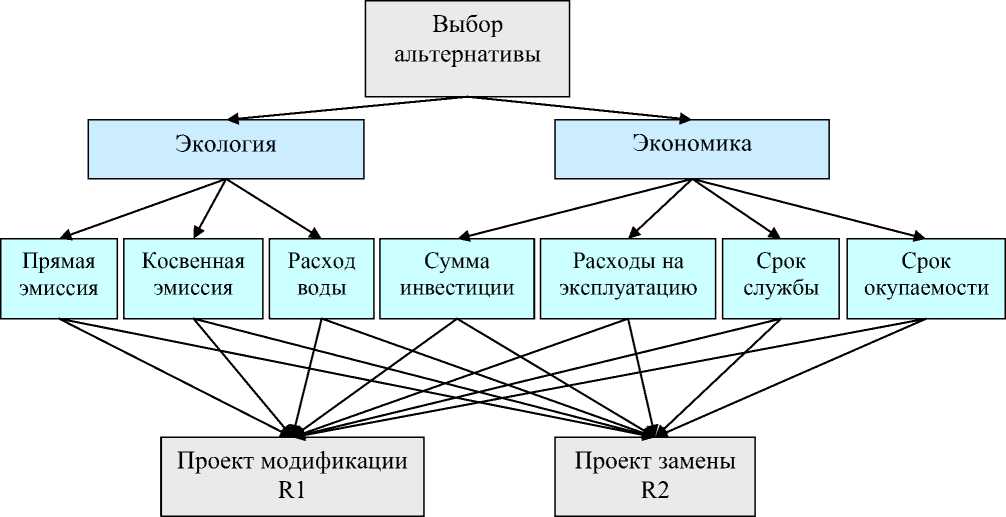
Рис.4. Модель метода АНР

Построение модели целевого программирования

Пусть даны N альтернативных проектов, которые будем рассматривать как переменные решения, обозначив их x i , где i=1,2,…, N. Определим x i = 1, если i-й проект выбирают, и x i = 0, если i-й проект отвергают. Переменные решения образуют вектор x=( x 1, x 2,…, x N ). Определим основные составляющие практической выгоды от реализации проекта, используя систему ИУР Комиссии ООН или иную систему. Выберем M индикаторов в качестве целевых параметров.

Обозначим k ij - значения j-го параметра, ассоциированные с i-м проектом. Поскольку целевые параметры измеряются в разных физических величинах нормализуем их значения. Возьмем в качестве нормирующего делителя значения j-го параметра исходного уровня:

k ij = z ij /w j ,                                                                                                 (1)

где w j – значение j-го параметра исходного уровня, z ij – значение j-го параметра после внедрения i-го проекта.

На основании значений параметров для исходного уровня ЛПР устанавливает желаемые значения z j^* целевых параметров после реализации проекта, а также допустимые отклонения от z j^* в лучшую сторону δ j⁺ ≥ 0 и в худшую сторону δ j^- ≥ 0.

Сформируем целевые функции:

k i1 x i + δ 1^- - δ 1⁺ = z 1^*

k i2 x i + δ 2^- - δ 2⁺ = z 2^*                                                                                   (2)

k iM x i + δ M^- - δ M⁺ = z M

Переведем целевые функции в систему ограничений, связанных с иными требованиями к проекту такими как лимит по бюджету, технические и эксплуатационные характеристики, срок окупаемости затрат на выполнение проекта и т.д. Эти ограничения задачи можно представить в виде равенств или неравенств.

Таким образом, задача приобретает следующий вид:

M

Min У 5:- -5/ jj j=1'

при условии:

kijxi + δj- - δj+= zj*, для всех i g N и j g M,                                                        (3)

kijxi = aj, для всех i g N и j g P kijxi < aj, для всех i g N и j g Q , где zj* - желаемое значение целевого параметра, δ+j, δ-j – допустимые отклонения от желаемого значения, множество N = {i | i cd ,i < N} ; множество M = {j | j c□, j < M}; множествоP = {j | j cd ,M < j < P}; множество Q = {j | j cd ,P < j < Q} ; при 8+j, 8-j > 0.

Для решения данной задачи используются известные алгоритмы решения задач одноцелевого целочисленного линейного программирования.

Построение модели метода ε – ограничений

Выберем одну из целевых функций, обозначив ее f p ( x ). Остальные целевые функции переведем в разряд ограничений, установив для каждой из них верхнюю границу 8j. Тогда задача одноцелевого программирования приобретает вид:

N

Min fp (x) =Z kipxi i=1

при условии:

k ij x i < e j , для всех i g N и j g M ,                                                     (4)

kijxi - aj = 0, для всех i g N и j g P kijxi - aj < 0, для всех i g N и j g Q , ej >0 ,для всех j g M, где множествоN = {i | i cd ,i < N} ; множествоM = {j | j cd ,j ^p,j < M}; множествоP = {j | j cd ,M < j < P}; множество Q = {j | j cd ,P < j < Q} .

Для минимизации k целей алгоритм генерации множества Парето состоит в выполнении пяти шагов:

• 1.    Решить k одноцелевых оптимизационных задач с первоначальными ограничениями для нахождения индивидуального оптимального решения для каждой из k целей.

• 2.    Вычислить значение каждой из k целей при каждом из найденных на первом шаге оптимальных значений других целей. Таким образом, получаем аппроксимацию диапазона значений для каждой цели. Возможное наименьшее значение k-ой цели является индивидуальным оптимальным решением. Наибольшее значение k-ой цели, найденное при минимизации других k-1цели, представляет собой приближенное максимально возможное значение цели во множестве Парето.

• 3.    Преобразовать многоцелевую оптимизационную задачу в одноцелевую задачу указанным выше способом.

• 4.    Выбрать r- желаемое число одноцелевых оптимизационных задач для генерации множества Парето (r≥M). Используя метод HSS, генерировать r комбинаций значений ε i.,…, ε l -1, ε l+1,…., ε k в пределах диапазонов значений к-1 целей, определенных на втором шаге.

• 5.    Решить установленную на шаге три одноцелевую оптимизационную задачу для каждой комбинации значений ε, определенных на шаге 4[10].

Совокупность решений, полученных на первом и пятом шагах, представляют собой аппроксимацию множества Парето, которая предоставляется на рассмотрение ЛПР. Поскольку число альтернативных проектов может оказаться достаточно большим, для выбора наиболее предпочтительного решения можно воспользоваться методом взвешенных сумм.

Пусть даны N альтернативных проектов, полученных в результате решения задачи методом ε – ограничений, которые будем рассматривать как переменные решения, обозначив их x i , где i=1,2,_, N. Переменные решения образуют множество = S = { x | x с , x <  N } . Предположим, мы имеем критерии выбора k с нормализованными весовыми коэффициентами Wj, причем Wj >  0 для всех j = 1,2,..., M и ^>_з = 1 . Тогда задача ^j = 1

одноцелевого программирования может быть представлена в виде:

NM

Min Z(x) = ££ W j k y X ij                                                   (5)

i = 1 j = 1

M при условии x G S, где w > 0 для всех j = 1,2,..., M, ^w = 1 и S- множество j=i допустимых решений.

Для нахождения наиболее предпочтительного решения алгоритм состоит из выполнения трех шагов:

• 1.    ЛПР проводит оценку весовых коэффициентов критериев.

• 2.    Рабочая группа решает одноцелевую оптимизационную задачу (6) и предоставляет результат ЛПР.

• 3.    Если результат отклоняется, ЛПР изменяет значения весовых коэффициентов w и повторяется шаг 2.

Оценка весовых коэффициентов критериев

При небольшом числе критериев оценку их весовых коэффициентов можно осуществить методом АНР. В противном случае целесообразно воспользоваться методом отношений, состоящим из выполнения двух операций:

коэффициента конкордации производится по критерию X Пирсона.

В интерактивном режиме работы с ЛПР при малой размерности задачи выбора проекта целесообразно воспользоваться методом АНР или целевого программирования.

В остальных случаях выбор проекта осуществляется с использованием методов целевого программирования или ε – ограничений. При определенных условиях можно применить оба метода, что позволит повысить достоверность решения задачи.

Заключение

Методы многокритериального анализа и оптимизации позволяют решать широкий спектр задач и могут быть использованы при модернизации, как отдельных предприятий, так и при выполнении региональных программ. Применение методов повышает обоснованность управленческих решений, показатель «стоимость-эффективность» и предоставляет возможность для интегрированного подхода к решению экономических, экологических, и социальных проблем в целях достижения устойчивого развития.

Предложенный инструментарий допускает решение задач различной размерности, при разных режимах работы лица или группы лиц, принимающих решение, и обеспечивает проверку достоверности предоставляемой ими информации.