Устойчивость и организационная структура технологических систем в трикотажном производстве

В работе [1] установлено, что технологическая система в трикотажном производстве среди возможных состояний может иметь такое состояние, пребывая в котором она в наибольшей мере способна противостоять действию внешних и внутренних факторов, стремящихся вывести ее из него. Иными словами, система в этом состоянии устойчива. Определение значений параметров устойчивого состояния технологических систем в трикотажном производстве представляется вполне актуальной задачей, формальное решение которой получено в [1] методом математического моделирования. Рассмотрим более подробно соображения, приводящие к системе дифференциальных уравнений, представленных в [1] в качестве модели технологической системы.

В основу алгоритма модели положена идея о переходном процессе, в ходе которого технологическая система из некоторого неустойчивого начального состояния переходит в конечное - устойчивое. При этом параметры системы изменяются свободно, отображая, своего рода, ее эволюцию в искусственно создаваемых нестационарных условиях, выражающуюся в движении ресурсов, схема которого представлена на рис. 1. Схема отображает распределение и движение ресурсов четырех видов по мере формирования устойчивой технологической системы на двух интервалах времени: на интервале времени ∆t, непосредственно следующим за моментом t 0 пуска системы, и на интервале, начиная с момента t >t 0 + ∆t. До момента t >t 0 + ∆t все N машин, единовременно введенных в работу, все сырье, необходимое для их заправки, а также обслуживающий персонал находятся в состоянии активного взаимодействия.

Результатом его является формирование устойчивой технологической системы с определенными значениями параметров состояния X(t) – численности работающего оборудования и Y(t) – численность вязальщиц, обслуживающих X(t) единиц оборудования. По достижении стационарного состояния на интервале t >t 0 + ∆t X(t) и Y(t) перестают изменяться. На схеме формирующейся технологической системе соответствует центральная область или ядро. Резервные ресурсы каждого из четырех видов отображены на схеме одноименными прямоугольными секторами периферической области вокруг ядра. В переходном процессе, связанном с заменой равенства X(t)=N на неравенство X(t)≠N, может происходить двухсторонний обмен ресурсами между резервами и ядром. Примем, что на интервале времени ∆t машины работают безостановочно. Тогда, начиная с момента t>t 0 , на интервале времени ∆t в технологической системе реализуется два процесса: изменение со скоростью dY(t)/dt численности вязальщиц, вовлеченных в работу, и изменение со скоростью dX(t)/dt численности работающего оборудования. При этом изменения параметров X(t) и Y(t) в переходном процессе могут происходить как в сторону увеличения, так и в сторону уменьшения. При определенном соотношении между численностью работающего оборудования X(t) и численностью Y(t) вязальщиц, вовлеченных в производственный процесс, скорости их изменения dX(t)/dt и dY(t)/dt станут равными нулю, и в системе установится равновесие. Практика свидетельствует о том, что это состояние устойчиво в отличие от исходного, в котором справедливо равенство X(t)=N=Const. Таким образом, с логических позиций существование состояния устойчивого равновесия технологической системы допустимо.

Рисунок 1 - Схема распределения и движения ресурсов в технологической системе в переходном процессе: стрелки на схеме указывают возможные направления движения ресурсов в процессе формирования устойчивой технологической системы

В работе [1] построена математическая модель, отображающая динамику технологической системы в описанных условиях, которая представлена парой нелинейных дифференциальных уравнений в виде:

dX/dt = - k1X + k2Y/X + k3Z/X dY/dt = - k4Y - k5Y/X + k6Z/X                            (1)

Система (1) имеет стационарную точку S, координаты которой определяются такими формулами:

Y s = k 6 Z/( k 4 X s + k 7 )

Значение X s может быть получено как решение кубического уравнения

AXs3 + BXs2 + CXs + D = 0 , где:                          A=k1k4; B=k1k5; C= - k3k4; D= - (k2k6+ k3k5)Z .              (2)

Соотношения, определяющие координаты стационарной точки, показывают, что X s , Y s определяются всеми шестью коэффициентами модели (1).

Рассмотрим на конкретном примере, к каким выводам можно прийти, анализируя технологическую систему с позиций устойчивости. Исследование проведем по фазовому портрету, изображенному на рис. 2. Вычисление параметров A, B, C, D, содержащихся в (2), и расчет координат точек фазовых траекторий выполнен при значениях коэффициентов k 1 … k 6 , приведенных в табл. 1. Оценки коэффициентов k i построены с использованием технико-экономических показателей работы технологической системы в производстве женских колготок из текстурированной капроновой нити “эластик” линейной плотности 2.2 текс и 3.3 текс на одноциндровых автоматах Programm фирмы Lonatti на Витебском ОАО “КИМ”.

Таблица 1 - Значения коэффициентов k 1 …k 6 математической модели (1)

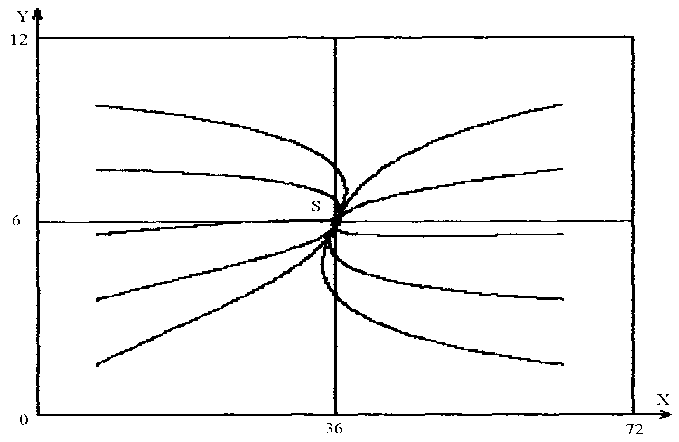
Рисунок 2 - Фазовый портрет технологической системы в производстве женских колготок из текстурированной капроновой нити “эластик” линейной плотности 2.2 текс и 3.3 текс на одноциндровых автоматах Programm фирмы Lonatti. Фазовые траектории направлены к точке S и сходятся в ней. Координаты точки S соответствуют устойчивому состоянию системы. Расчет координат точек фазовых траекторий выполнен по модели (1) при значениях коэффициентов k 1 …k 6 , содержащихся в табл. 1

Фазовый портрет показывает, что составляющие его траектории, начинающиеся в различных точках фазовой плоскости X,Y, определяемых начальными условиями, сходятся к точке S, имеющей координаты Xs, Ys. Вид и  направление кривых, а также характер их приближения к точке S позволяют заключить, что данная точка относится к типу, называемому асимптотически устойчивым узлом. Таким образом, при любых начальных сочетаниях значений параметров состояния X и Y технологическая система, моделируемая уравнениями (1), при значениях коэффициентов k1… k6, взятых из табл. 1, стремится перейти в состояние со значениями этих параметров, равными Xs, Ys, определяющими положение стационарной точки. Следовательно, существование среди множества возможных состояний технологической системы устойчивого стационарного состояния, а также его достижимость получают подтверждение на уровне математического моделирования.

Результаты моделирования и анализа устойчивости технологических систем в трикотажном производстве позволят сделать некоторые обобщения относительно структурной организации таких систем и особенностей их функционирования. Прежде всего, отметим, что такое качество, как устойчивость рассмотренных систем, отражается в характере изменения параметров, важных с позиций существования и оптимального функционирования таких систем. Моделирование показывает, что устойчивая технологическая система характеризуется определенными значениями параметров X, Y, Z: X=X s , Y=Y s и Z=1, 2,…. Она с полным основанием может рассматриваться как своего рода структурная ячейка производственного участка или цеха, включающего М таких систем, функционирующих независимо друг от друга.

Следует обратить внимание еще и на то, что устойчивая технологическая система, характеризующаяся значением Z=2 ,не эквивалентна совокупности двух технологических систем, соответствующих Z=1, т. к. при Z=2, т.е. при двух поммастерах, обслуживающих одну рабочую зону, вероятность немедленного обслуживания машины после момента ее остановки выше, чем при Z=1. Иными словами, в устойчивой технологической системе со значением Z=2 действуют иные взаимосвязи, чем в системе с Z=1. Это представляется достаточно очевидным и apriory. Однако то, что данная особенность отображается построенной математической моделью, свидетельствует в пользу информативности этой модели и адекватности описания ею производственной реальности.

При построении математической модели технологической системы в трикотажном производстве использован ряд логических, технологических, математических соотношений, в основе которых лежат простые и вместе с тем очень характерные для существующих систем свойства, особенности и принципы. Исследование моделей, построенных с учетом этих условий и требований, показывает, что технологические системы, включающие машины, работников, сырьевые ресурсы и организованные в соответствии с определенными требованиями и принципами, будут устойчивыми лишь при определенных значениях параметров, определяющих их состояние.