Устойчивость энергосберегающей адаптивной радиальной гидростатической опоры с ограничением выходного потока смазки

Бесконтактные газостатические и гидростатические опоры (АГСО), в которых уменьшение податливости до нулевого и отрицательных значений обеспечивается за счет ограничения выходного потока смазки (АГСО-ВП) [1], в сравнении с адаптивными опорами с входными регуляторами расхода (АГСО-РР) обладают лучшими статическими характеристиками – более широким адаптивным диапазоном нагрузок, стабильностью характеристики податливости, значительно меньшим расходом смазки [2, 3]. Известно, что в существующих конструкциях АГСО-РР с уменьшением податливости значительно ухудшается качество динамики. Это объясняется негативным влиянием повышенной чувствительности входных регуляторов расхода к изменению давления смазки [4]. В АГСО-РР для обеспечения режима отрицательной податливости применяют единственное известное на настоящее время эффективное средство подавления неустойчивости – систему двойного дросселирования смазки в магистрали нагнетания, в которой регулятор выполняет функцию основного сопротивления, а дополнительные пассивные дроссели на входе в несущий слой – функцию демпфера вибраций [5]. В АГСО-ВП из-за

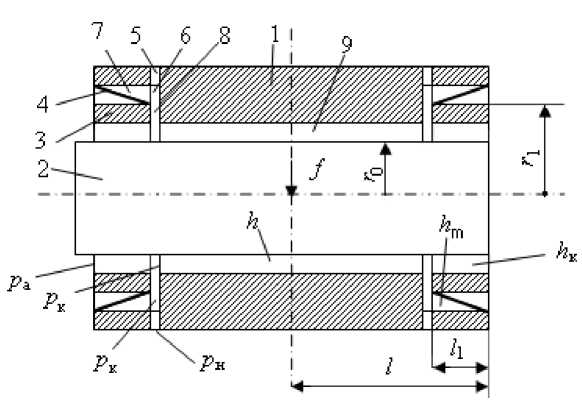
Рис. 1. Расчетная схема опоры отсутствия входных регуляторов и, как следствие, сниженного энергопотребления проблема обеспечения устойчивости опоры, по-видимому, не стоит так остро. Поэтому устойчивость конструкции на режимах неположительной податливости, вероятно, может быть обеспечена без привлечения дополнительных средств демпфирования вибраций. Кроме того, смазочный слой толщины hm активного ограничителя выходного пока смазки, который расположен под мембраной (рис. 1), сам по себе может играть роль демпфера, способствуя тем самым улучшению динамики опоры.

Тем не менее, повышенный градиент давления в несущем слое смазки может стать причиной снижения показателей устойчивости такой опоры. Целью настоящей работы является теоретическое изучение устойчивости радиальной гидростатической АГСО-ВП одинарного дросселирования, расчетная схема которой показана на рис. 1. Описание конструкции опоры и анализ ее статических характеристик приведены в работе [3].

Математическая модель динамики опоры

Как и при исследовании статических характеристик АГСО-ВП [3], моделирование нестационарного радиального движения опоры основано на том, что соблюдается параллельное расположение осей корпуса и подвижных элементов (рис. 1). Исследование проведено в безразмерной форме. За масштабы основных величин приняты: радиус r ₀ вала - для линейных размеров, давление p _н источника питания опоры - для давлений, п r ₀ ² p _н - для сил, h ₀ ³ p _н / 6 р - для объемных расходов жидкости, h ₀ - для зазоров и эксцентриситетов подвижных элементов, 1 ₀ - для текущего времени. Здесь h ₀ - толщина h несущего смазочного слоя при соосном расположении элементов (при отсутствии нагрузки f ), р - вязкость смазки. Далее безразмерные величины обозначены прописными буквами.

Динамическая функция P ( Z , ф, т) распределения давления в тонких смазочных зазорах для несжимаемой смазки удовлетворяет нестационарному дифференциальному уравнению Рейнольдса [6]

6 Lt36P) б(тт38P) dH, — I H 3 — l +—I H 3— 1 = о —i, 8ф ( 8ф J 8Z ( 8Z J dT

где H i (ф, т) = 1 - e i (t) Cos(ф) - функция радиального смазочного зазора между несущими поверхностями смазываемых элементов конструкции, Z , φ – продольная и окружная координаты, τ – безразмерное время, ε i = ε – эксцентриситет вала 2 и корпуса 1, ε i = ε m – эксцентриситет колец 3 и вала 2, ε _k = ε – ε _m эксцентриситет вала 2 и подвижных колец 3,

12К pн h0t0

– безразмерный параметр, называемый «числом сдавливания» смазочной пленки [7].

По аналогии с [3] при математическом моделировании предполагали, что продольный размер втулки 3 мал по сравнению с ее диаметром. В этом случае при наличии продольных микроканавок в междурядной области влиянием окружных перетоков смазки в зазорах можно пренебречь (∂P/∂φ = 0). При этом уравнение (1) упрощается и принимает вид г P  H

—т = ^ст —₃ ■

8 Z ²     H 3

i

Уравнение (3) по областям интегрирования имеет следующее аналитическое решение:

P (Z , ф , т ) ^

о н

2 Hk oH

2 H³

L - Z

Z ( Z - L^ + P_k ( ф , т ) —--для зазора в торцевой области,

L

( Z ² - L ^ ) + P_k ( ф , т ) - для зазора в междурядной области,

•

°Hm-Z(Z -2Lx)+pk(ф,т)- для зазора под мембраной, 2 H ™ где Pk(ф, т) - функция давления на выходе питающей щели 5, L 1 - ширина колец 3, L2 - половина ширины междурядной области несущего слоя.

Решение (4) получено при использовании очевидных граничных условий для функции P :

P (0, ф , т ) = P k ( ф , т ), P ( L₁, ф , г ) = 0 - для зазора в торцевой области,

dP

< — (0, ф , т ) = 0, P ( L,, ф , т ) = P, ( ф , т ) - для зазора в междурядной области, d Z'

дP

P (0, ф , т ) = P_k( ф , т ), — ( L , ф , т ) = 0 - для зазора под мембраной.

I                    дZ

Безразмерный объемный расход смазки через любое сечение Z = Z ₀ радиального зазора определяется формулой [6]

Q = - H i— ( z 0 , ф,т ).

С учетом этого и (4) нестационарное уравнение баланса расходов смазки на выходе одной щели и входе в несущий слой опоры примет вид

•               •               •

A_H ( ¹ - P ) = H I — + — ¹ Hк + ^ L₂ H + ^ L Hm, »_v k, k L 2 k 2          1 m"

где A – параметр, определяемый постоянными размерными величинами зазора входной щели [ ].

Несущая способность соответствующих радиальных смазочных зазоров определяется формулой

. 2 n                    L i

W i = - J Cos( ф )d ^ j p ( Z, ф , т ) dZ .

^п 0             0

Выполнив интегрирование функции давления (4) по координате Z , получили формулы для определения несущей способности зазоров для половины междурядной и торцевой области несущего слоя и в области зазора, расположенного под мембраной:

2 п

W =

L 2 f p п J P k

V

•

LH 3 h 3 v

Cos ( ф ) й ф ,

2 п

^Wk =

I 2п п IP

2 п

• \

LH I

•

Cos ( ф ) d ф ,

W = rr m

RA f p п J k

V

L 1 ² H m

³ H m ,

) Cos ( ф ) d ф ,

где ^R , ^- наружный радиус подвижных элементов 3.

С учетом (6) формула для нестационарной несущей способности опоры такова:

W=

? 2 п Гт Л

2( W _c+ W J = 2   [ L i + l ] p

п J0 V2 v

••

_ LH

12 H k ³   3 H ³

Cos ( ф ) d ф .

Ввиду малой массы подвижного элемента 3 связанная с ним сила инерции будет пренебрежимо мала по сравнению с воздействующими на него гидравлическими силами. В этом случае радиальное смещение е _m втулки под влиянием воздействующих на нее сил давления W_m и W k , уравновешиваемых силой упругого сопротивления мембраны, в соответствии с законом Гука может быть представлено уравнением

2 п

•

Sm =" Km ( Wm " Wk )="

K m ' Г к (D.^P+Ll HK п ^{J 1 ( 1}    , ) P^k 12 H k

V

k

е

•

4^ 1 1^ H m

VJ

Cos ( ф ) d ф ,     (8)

где K m – безразмерная радиальная податливость материала мембран.

Масштаб текущего времени определен из условия равенства единицы безразмерной массы вала: ^mh 0 / ⁿ r 0² p н t 0² = 1, где m ^- масса вала.

С учетом силы инерции массы вала и формулы (7) уравнение баланса сил, действующих на вал 2, примет вид

•             •

2 2г ' Г L ₊ L ) p - LH — L ^H n J I 2 ^{2 J k} 12 H k 3 H³

••

Cos ( ф ) d ф + £ = F,

где F – приложенная к валу 2 внешняя возмущающая сила (нагрузка на опору).

Воспользовавшись уравнением (5) и очевидным соотношением е k = е - е m , величины е k и P_k исключили из рассмотрения. С учетом этого нестационарные уравнения (8) и (9) будут представлять математическую модель динамики АГСО-ВП, которая в данном случае является нелинейной системой автоматического регулирования с возмущающей входной величиной F и выходными величинами е и е m .

Линеаризация математической модели и передаточная функция податливости опоры

Исследование устойчивости АГСО-ВП проведено с использованием линейных методов теории автоматического регулирования [8]. Для этого выполнена линеаризация нелинейностей в уравнениях математической модели в окрестности установившегося режима работы опоры. Всякую динамическую величину представляли в виде X (т) = X , + А X (т), где X , соответствует установившемуся режиму, A X - малое динамическое отклонение величины X от X 0 .

Процедура линеаризации позволила вывести величины отклонений динамических функций за знак интеграла в уравнениях (6)-(9) и тем самым привести интегралы к виду, когда подынтегральные функции становятся зависимыми лишь от окружной координаты. Это дает возможность провести их интегрирование численным методом (вычисления проводились с использованием метода Симпсона [9]). Затем к уравнениям модели, записанной в отклонениях, применено интегральное преобразование Лапласа [8]. В результате получена система линейных уравнений относительно изображений малых отклонений величин модели

(B0 + C2 s )А£ + (C0 + C1 s )А£„ = 0,

(B4 + C3 s + s2 )А£ + (- B4 + C4 s )A£m = AF, где – лапласовы трансформанты отклонений соответствующих динамических величин, s – переменная преобразования Лапласа. Входящие в уравнения константы вычисляются по формулам

2 п                   2 n                             2 n                   2 n B 0 = J « 0 d 2 d ф , B 1 = J ( « 0 d 3 + d 7 ) d ф , B 2 = J a 0d 4 d ф , B 3 = J ( « 0 d 5 + d 6 ) d ф , 2 п                     2 П                                2 п                                2 п B 4 = J а 3d 2 d ф , B5 = J ( a 3d 3 + d 8 ) d ф , B 6 = J ( a 0d 4 + d 9 ) d ф ,В 7 = J a 3d 5 d ф , 00    0    0

- 1

d 0 = A H L 1 , d 1 = ( d 0 + H k3 ) , d 2 = 3 d 0 d 12 H ^ Cos ² ( ф ), d ₃ = 0, 5 ^ 1. 1 d 1 Cos ² ( ф ),

, _ _{T T} 2z х , _ г 2      2z х , _ COS 2 (^) , _     COS 2 (^) , _   COS 2( ф )

d 4 a L L ² dCos ^{( ф )}, d 5 a L d 1 Cos ^{( ф )}, d 6 a 1         , d 7 ^a 2         , d 8 ^a 4

HmHkHk

Cos 2(ф)    _ LiKm (2 Ri - 1)      aL KmRi    _ дД Km      Li + 2 L 2

d9 = a5  H3  ’a0 =     2n     ’ai =   3n   ’a2 =   2П a = n   ’ a4 = 6n’ a5 = ^C Cо = 1 - Bo, Ci = Bз — Bi, C2 = Bi + B 2, Cз = B5 + B 6, C4 = B7 — B5.

Исключив из (10) величину A ^ _m , посредством несложных преобразований нашли передаточную функцию

ф(5)=#=. C/C'.’(11)

A F а о + a i 5 + а 2 5 + a 3 5

где a0 = B4(C0 + B0), ai = B4Ci + C0C3 — B0C4 + B4C2, a2 = C0 + CiC3 — C2C4’ a3 = Ci"

Передаточная функция (11) является лапласовой трансформантой динамической податливости опоры, а ее знаменатель - характеристическим полиномом динамической системы. Статическая податливость опоры определяется величиной K = C 0 а ₀.

Результаты исследования устойчивости опоры

Свободное радиальное движение опоры оценивали с помощью корневых критериев качества её динамики: нормированной степени устойчивости n₀ = -Max Re { s k }e [0;1], которая обратно пропорциональна продолжительности переходного процесса, где s k _- корни нормированного характеристического уравнения математической модели [8]; затухания колебаний за период ^ = [1 - Exp(-2n n₀ / IP!)] 100% е [0;100%], где в — мнимая часть корня s_k , для которого Re ^{ s k } = ^-П о . ^{Достаточно} высокими значениями этих критериев ^{можно считать} П о > 0,1 ^- 0,2; ^ > 60%. Критерий п₀ определяет быстроту затухания переходного процесса, ^ - его колебательность. Запас устойчивости опоры оценивали по показателю колебательности M , который характеризует относительную величину резонансного пика амплитудно-частотной характеристики (АЧХ) частотной передаточной функции, которая получается из (11), либо аналогичной передаточной функции формальной заменой s = i Q, что соответствует переходу от преобразования Лапласа к преобразованию Фурье, где Q - безразмерная частота колебаний, i - комплексная константа [8].

В качестве входных параметров использованы: податливость K m материала мембраны; наружный радиус R 1 кольца 3; L - половина длины опоры; х е [0;1] - нормированный коэффициент настройки входной дросселирующей щели 5 при соосном расположении подвижных элементов и отсутствии нагрузки на опору, и «число сдавливания» σ, оказывающее влияние лишь на динамику опоры.

На рис. 2 изображены графики функции п₀ (о) для различных значений нагрузки F на вал 2 для K_m = 8,98 и χ = 0,38, при которых опора имеет наиболее близкую к постоянной величине отрицательную податливость при малых и умеренных значениях F (на рис. 3 представлены – 679 –

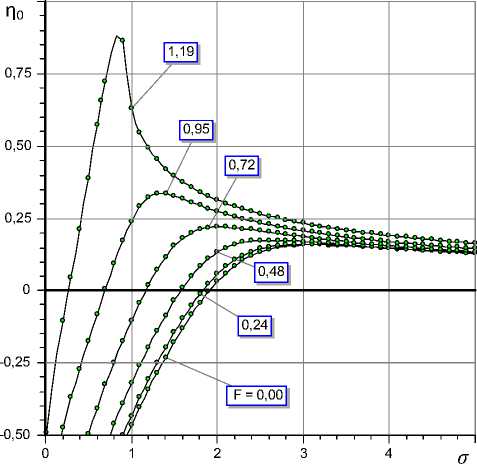
Рис. 2. Зависимости нормированной степени устойчивости η₀ от числа сдавливания σ и внешней нагрузки F при L = 1,5; L 1 = 0,3; R 1 = 1,2; χ = 0,38; K_m = 11,23

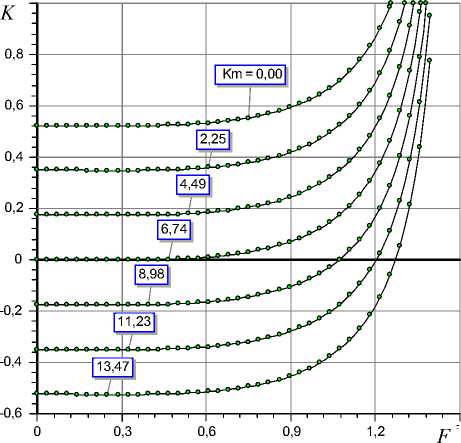
Рис. 3. Зависимости статической податливости K от внешней нагрузки F и податливости мембраны K_m при L = 1,5; L 1 = 0,3; R 1 = 1,2; χ = 0,38

графики зависимости податливости опоры от внешней нагрузки). Видно, что длительность переходного процесса в опоре экстремально зависит от «числа сдавливания» смазочной пленки. При малых σ опора неустойчива (η < 0), левой от максимума ветви функции η (σ) устойчиво работающей опоры (η0 > 0) соответствует колебательный переходный процесс (ξ < 100%), пра-– 680 – вой – апериодический (ξ = 100 %). С увеличением нагрузки F на опору область устойчивости по параметру о расширяется. При этом наблюдается заметный рост п0. Это означает, что нагружение вала является фактором стабилизации и повышения быстродействия АГСО-ВП. Вместе с тем, как показывают графики рис. 4, для критерия £ затухания колебаний за период обеспечиваются и показатели этого критерия достаточно высокие (ξ > 80%), что свидетельствует о приемлемом качестве динамики свободных колебаний опоры.

Из рис. 5, на котором показаны графики зависимости n₀ ( F ) при различных значениях K m , видно, что по аналогии с о этот параметр также доставляет максимум функции быстродействия. Действительно, с увеличением K m в целом наблюдается рост кривых n₀ ( F ), затем их снижение. Сравнение данных графиков с графиками рис. 3 позволяет сделать интересный вывод о том, что максимум быстродействия наблюдается в области K_m , соответствующих нулевой податливости опоры ( K = 0). Видно, что быстродействие такой опоры примерно втрое больше, чем у обычной гидростатической опоры ( K m = 0). Скорее всего, этот факт объясняется специфическими демпфирующими свойствами смазочного зазора, расположенного под мембраной. Вместе с тем с увеличением K_m (при K_m > 9 для приведенных на рис. 5 графиков) в области отрицательной податливости ( K < 0) быстродействие опоры заметно снижается и начиная с определенного значения K m опора теряет устойчивость во всей области воспринимаемых нагрузок.

Для оценки запаса устойчивости линейных динамических систем часто используют показатель колебательности M = Max A (Ω) (резонансный пик кривых), где A (Ω) – АЧХ какой-либо частотной передаточной функции изучаемой динамической системы [8]. Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик АЧХ. Допустимое значение показателя колебательности для хорошо демпфированных систем не должно превосходить M = 1,5, однако допустимо и M < 2,5 [8].

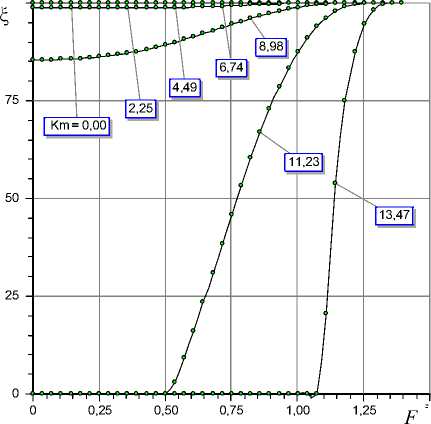
Рис. 4. Зависимости показателя затухания колебаний за период ξ от внешней нагрузки F и податливости мембраны K m при L = 1,5; L 1 = 0,3; R , = 1,2; х = 0,38; о = 4

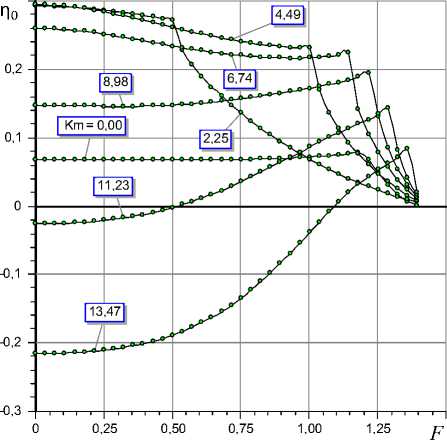
Рис. 5. Зависимости нормированной степени устойчивости п 0 от внешней нагрузки F и податливости мембраны K m при L = 1,5; L 1 = 0,3; R 1 = 1,2; х = 0,38; о = 4

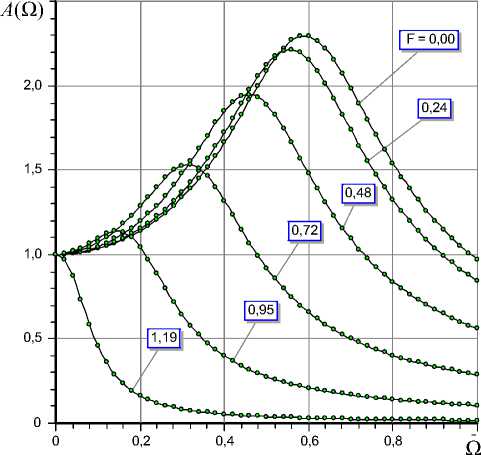
Рис. 6. Амплитудно-частотные характеристики A ( Q ) опоры для различных значений внешней нагрузки F при L = 1,5; L , = 0,3; R , = 1,2; х = 0,38; K m = 8,98, о = 4,5

Для АЧХ, соответствующей частотной передаточной функции (11) динамической податливости адаптивных опор, подобный подход к определению запаса устойчивости неприменим поскольку, например, для опор нулевой статической податливости расчет показателя колебательности заведомо давал бы бесконечно большую величину. Для корректного применения – 682 – критерия M необходимо использовать другую передаточную функцию. Для рассматриваемой конструкции, которая работает на режимах нулевой или отрицательной податливости, такой функцией может быть, например, реакция опоры на внешнее силовое воздействие F в виде перемещения εm кольца 3 относительно корпуса 1. Соответствующая передаточная функция имеет вид

A ^ m

^Ф m ⁽ S ) = — A F

B0 + C2 s a 0 + a1 s + a 2 s + a 3 s

На рис. 6 показаны АЧХ A(Q) = |Ф _m ( i Q) / Ф _m (0) | частотной передаточной функции Ф _m для режима статической отрицательной податливости. Из них следует, что АЧХ имеют экстремальный характер, что свидетельствует о склонности такой опоры к колебаниям.

Из графиков видно, что при малых и умеренных нагрузках ( F < 0,7) пики кривых не превосходят M = 2,5, что свидетельствует об удовлетворительном запасе устойчивости опоры. Для больших нагрузок ( F > 0,72) характерно M < 1,5, т. е. при нагружении опора становится хорошо демпфированной системой, что подтверждает ранее сделанный аналогичный вывод относительно качества свободных колебаний опоры.

Заключение

На основании проведенного исследования можно сделать заключение о том, что радиальная опора с ограничением выходного потока смазки может работать устойчиво на режимах отрицательной податливости. При этом обеспечиваются приемлемые показатели качества динамики свободных и вынужденных колебаний. Область отрицательной податливости устойчивой опоры ограничена определенным значением параметра K_m . АГСО-ВП отрицательной податливости при одинарном дросселировании входного потока смазки склонна к колебаниям и обладает достаточным запасом устойчивости лишь в этой области. С дальнейшим ростом параметра K m динамика опоры существенно ухудшается и она становится неустойчивой.

Определенные перспективы расширения области отрицательной податливости и повышения запаса устойчивости опоры могут быть связаны с установкой дополнительного демпфирующего сопротивления на входе в несущий слой, т. е. с введением в конструкцию системы двойного дросселирования, использование которой для этих целей в известных конструкциях адаптивных опор неизменно давало положительный эффект.