Устойчивость к сдвигу метода идентификации дактилограмм по полю направлений

Для решения задачи персональной идентификации разрабатываются гибридные оптикоцифровые устройства, в которых распознавание контурных изображений основано на оптическом выполнении преобразования Радона [1,2]; на анализе пространственного спектра Фурье изображения с помощью фотоприемника с кольцевыми и чувствительными секторными элементами [3]; на использовании совместной корреляции двух изображений с помощью фоторефрактивных кристаллов [4]. В некоторых существующих системах отпечатки пальцев вводятся в компьютер в реальном времени с помощью призмы, используемой в режиме полного внутреннего отражения [3-5]. Быстрый оптический ввод отпечатка пальца в память компьютера и оптическая предобработка изображения существенно ускоряют процесс распознавания и в этом преимущество гибридных систем перед цифровыми.

Однако существующие системы идентификации дактилограмм имеют ряд недостатков. Анализ и классификация структуры полос дактилограммы (папиллярного узора) с помощью оптической нейронной сети, предназначенной для выделения участков прямых линий на изображении методом пре- образования Радона [1], или с помощью подсчета числа Галтона (число бифуркаций и центров полос дактилограммы) [2] являются операциями с определенными затратами машинного времени. Это связано с наличием высокой пространственной несущей частоты на дактилограмме, которая затрудняет поэлементную обработку изображения. Анализ дактилограмм с помощью обработки пространственного спектра [3] хотя и является более быстрым вариантом распознавания, но обладает низкой достоверностью, т.к. является инвариантным к перестановке участков на изображении. В [6] предложен метод оптического построения поля направлений структурно избыточных изображений. Этот метод позволяет эффективно сжимать информацию, содержащуюся в изображениях с несущей пространственной частотой. Он основан, фактически, на замене участка изображения одним числом, равным среднему углу наклона полос на данном участке. В [6] описан численный эксперимент по идентификации дактилограмм (для 10 различных пальцев) с помощью полей направлений (выделялось 8 направлений), который продемонстрировал высокую надежность идентификации по сравнению с методом Фурье-спектра. В [7] описан оптико-цифровой эксперимент по идентификации дак- тилограмм. Но в работе [7] был проведен эксперимент с относительно небольшим набором базовых отпечатков, поэтому трудно сказать, как метод будет работать если число базовых дактилограмм существенно увеличится. В данной работе приведены результаты оптико-цифрового эксперимента по определению устойчивости метода распознавания к сдвигу. В эксперименте использовалось 100 различных пальцев, для которых строилось поле направлений по 4 направлениям: 0, 45, 90, 135 градусов.

1.    Теоретические основы метода идентификации дактилограмм

Поле направлений изображения - это функция координат точки, равная углу касательной к линии уровня интенсивности изображения. Так, если I ( x,y ) есть интенсивность света в изображении, то поле направлений ср(x,y ) определяется соотношением:

д I ( х , у )/ д х

, д I(х,у)/ду                   (1)

0 <  ф (х , у ) <  п .

Очевидно, что угол ^ ( х,у ) задает направление, перпендикулярное вектору градиента

(б I (х, у)/дх ,д I (х, у)/ду).

Реализовать оптическими средствами формулу (1) не представляется возможным. В [6] предложена многоканальная оптическая схема для параллельного построения N “частных” изображений. В этом случае в корреляторе в частотной плоскости располагается пространственный фильтр в виде амплитудного (или фазового) транспаранта, состоящего из бинарных дифракционных решеток, делящих угол в 180 ° на N секторов, другая часть фильтра не пропускает свет. На во входной плоскости коррелятора помещен отпечаток пальца на стекле. Хотя сектора решетки, формирующие “частичные” изображения не пересекаются, каждая точка исходного изображения, в принципе, вносит вклад в каждую точку “частичного” изображения. Изображения со структурной избыточностью (контурные изображения типа отпечатков пальцев) состоят из большого числа линий с характерным периодом или из участков дифракционных решеток, пространственный спектр каждой из которых вносит вклад только в один из угловых секторов фильтра. Поэтому следует ожидать, что “частичные” изображения будут почти ортогональны. Т.е. “интеграл перекрытия” двух “частичных” изображений будет много меньше суммарной энергии каждого из них: от

jjIn (х,у)Im (х,у)dxdy << -от от

• << jj In (х, у ^^х;<1у -от

  
  

Если неравенство (2) не выполняется, то можно осуществить операцию ортогонализации “частичных” изображений по правилу:

1, Ik(х, у ) = max{In(х, у)}

n

о, Ik (х, у )* max {In (х, у)}’

n где max {...} n

- максимальное значение функции в точке среди функций с номерами n = 1, N .

Из уравнения (3) видно, что “частичные” изображения ~ ( х , у ) представляют собой ортогональный набор бинарных функций. Они позволяют вместо поле направлений по более формуле

N _~

ф ^{( х} , у )=& n I n ^{( х} , у )

n = 1

Ф n

п n

N

Далее полученное поле направлений, разлагается в ряд по некоторому ортогональному базису. В [6] показано, что базис бинарных функций Адамара предпочтительнее, чем базис Фурье. Несколько первых коэффициентов разложения составляют вектор признаков поля направления.

Функции Адамара определяются, как известно, следующим образом [8]:

1 от

hadm (t) = (T )-2 Oh-d...(t)]m‘ ,            (5)

k = 0

где m . - разряд кода Грея номера m , rad_m ( t ) - функция Радемахера. Код Грея образуется из номера m по следующему правилу:

• m. = m. ® m.+1,

  
  

где k - номер двоичного разряда (справа налево), m k - двоичный разряд в двоичной записи номера m :

от m = z mk2 k k =0

знак ® - означает сложение по мо- дулю 2. Функция Радемахера определяется следующим образом:

radm (t) = sgn [sin(2 m п11T)],                 (7)

где sgn - знаковая функция.

Идентификация отпечатков пальцев осуществляется с помощью поиска минимального евклидова расстояния между векторами признаков анализируемого изображения и набора эталонных базовых изображений. Евклидово расстояние определяется выражением:

r = У fe^{( k} )-a^(k ) ] 2 mn           m ^wn

k = 1

где b m^k )

(k)

и an - k-ые коэффициенты m-го базового и n-го анализируемого векторов признаков,

K - число коэффициентов разложения Адамара полей направлений.

Надежность идентификации дактилограммы в работе [7] характеризовалось параметром R :

R i =

_r ( i )__r( i )

r ₀      r ₁

r ₁

где r0 и r1 - минимальное и ближайшее к нему значения расстояний между анализируемым i-ым вектором и базисными векторами. Такое определение параметра R, как параметра характеризирующе- го разделенность классов не вполне корректно, т.к. в этом случае параметр R по-разному соотносится с базовым и анализируемым вектором. Поэтому будет целесообразно определить параметр R*, который определяется:

R i =

( i )           ( i )

0       ^r 1

( i )          ( i )

^r 0   + ^r 1

Средняя надежность метода идентификации характеризуется величиной:

2 M

) Ц = (2 M )"* £Ri, i=1

где 2 M - число анализируемых и базисных дактилограмм.

2.    Экспериментальные результаты

Отпечаток пальца на стекле помещен на вход когерентного Фурье-коррелятора, в частотной плоскости которого расположен пространственный фильтр в виде фазового транспаранта из бинарных дифракционных решеток, делящих 180 ° на 4 сектора, другая часть фильтра не пропускает свет. На выходе коррелятора регистрируется набор изображений, отличающихся от исходного (входного) изображения тем, что каждое из них имеет только часть спектра, попадающую в соответствующий сектор. Так как каждый сегмент фильтра представляет собой амплитудную бинарную дифракционную решетку, то после каждого сектора сформируется пара симметричных изображений. Таким образом, из 8 полученных изображений неповторяющихся только 4. Далее эти 4 изображения в компьютере совмещаются в одно изображение с весами, соответствующими сектору и равными углу наклона полос на изображении отпечатка пальца. В экспериментальной установке использовался фильтр с периодом дифракционных решеток 20мкм.

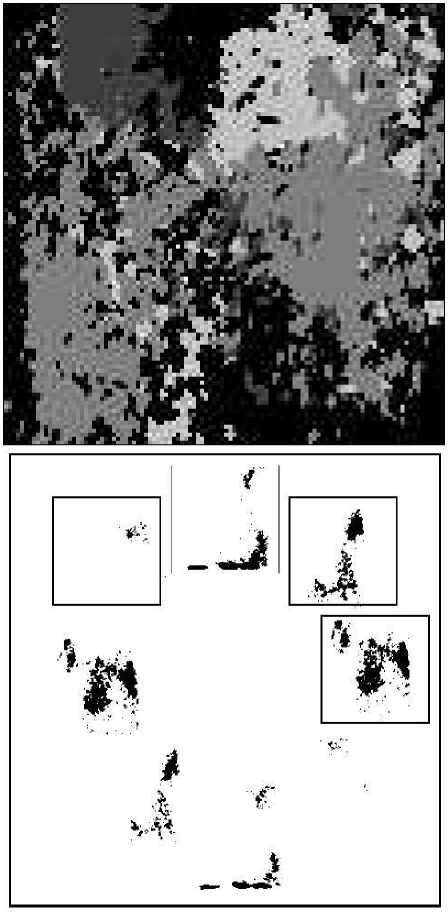
В эксперименте получены частичные изображения, показанные на рис. 1а.

Четыре из них участвовали в построении поля направлений, рассчитанному по формуле (4). Это поле показано на рис. 1б. Размер частичных изображений был 110 x 110 пикселов, все поле изображения имеет размер 512 x 512 пикселов. Физический размер поля телекамеры составлял 10 x 10мм, физический размер частичного изображения составляет около 2мм.

а)

б)

Рис.1 Экспериментальные “частичные” изображения (а) и поле направлений, полученное из них по формуле (4) (б)

Вектора признаков составлялись из коэффициентов разложения по базису Адамара полей направлений отпечатков. и определялось евклидово расстояние r mn от вектора каждого сдвинутого отпечатка до вектора каждого не сдвинутого отпечатка по формуле (8): во всех экспериментах использовались первые 16 коэффициентов разложения Адамара. Сдвиг осуществлялся с интервалом 0,5мм на расстояние до 4мм.

На рис.2 изображен график евклидового расстояния r mn между вектором признаков a 3 и 8 векторами признаков сдвинутых на расстояние d отпечатков одного пальца.

Для того, чтобы определить насколько метод распознавания устойчив к сдвигу, необходимо знать среднее минимальное расстояние между векторами признаков и дисперсию. Среднее минимальное расстояние между 100 не сдвинутыми векторами в 16 мерном пространстве признаков =0,085. Дисперсия - D=0,00044.

Для 50 векторов было получено: =0,089

D=0,00045. Вероятность того, что r> согласно [9]

и

N r

P {r >

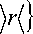
= 0.5 -Ф

A

N

r

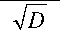
где N - общее количество анализируемых отпечатков, N r - количество отпечатков правильно идентифицированных.

r

0,07

0,06

0,05

0,04

0,03

0,02

0,01

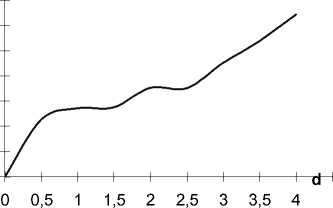
Рис. 2 График зависимости расстояния между векторами признаков не сдвинутого на расстояние d и сдвинутого отпечатка пальца.

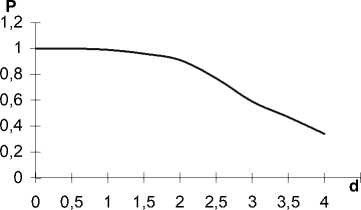
Рис.4 График зависимости вероятности правильного распознавания P от величины сдвига исходного изображения, рассчитанный по формуле (12).

На рис 3 изображен усредненный график зависимости расстояния вектора сдвинутого отпечатка от вектора не сдвинутого отпечатка.

r 0,1

0,08

0,06

0,04

0,02

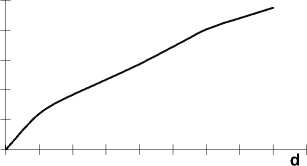
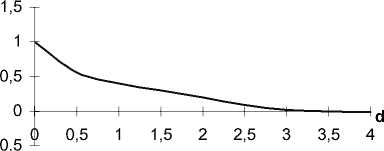
Рис. 5 График зависимости параметра от величины сдвига исходного изображения.

Рис.3 Усредненный по 100 векторам признаков график зависимости расстояния между векторами признаков сдвинутого и не сдвинутого отпечатка пальца.

Зная эту зависимость можно по формуле (12) рассчитать зависимость вероятности правильного распознавания P от величины сдвига.

График этой зависимости представлен на рис. 4.

На рис.5 изображен график зависимости параметра < R > от величины сдвига.

Из сравнения рисунков 4 и 5 видно, что при =0, K=0.5, т.е. как и предполагалось положительное значение параметра позволяет утверждать, что правильная идентификация преобладает над ошибочной.

В качестве базовых в эксперименте используются не сдвинутые отпечатки в качестве анализируемых сдвинутые. На рис. 6 изображен график надежности распознавания K от величины сдвига полученный обработкой экспериментальных данных, где K определяется по формуле:

K

1,2

0,8

0,6

0,4

0,2

00,511,522,533,54 ^d

Рис.6 График зависимости надежности распознавания K от величины сдвига исходного изображения, полученный экспериментально.

Для эксперимента с большим количеством дактилограмм величины K и P должны совпадать. Из рисунков 4 и 6 видно, что для 100 дактилограмм значения K и P совпадают с хорошей точностью (<5%). Т.к. при уменьшении количества векторов в эксперименте не произошло существенного изменения значений и D, то можно будет использовать формулу (19) для примерного расчета надежности метода распознавания для большого количества от- печатков (>100), используя при этом данные (,D), полученные в эксперименте c небольшим количеством базовых отпечатков.

Заключение

Представлены результаты натурного эксперимента по исследованию устойчивости к сдвигу исходного изображения метода идентификации дактилограмм по полю направлений. Показано, что надежность данного метода при сдвигах менее 2,5 мм превышает 0,9. Теоретически обоснована возможность применения результатов данного эксперимента для оценки надежности работы метода с более большим количеством отпечатков пальцев.