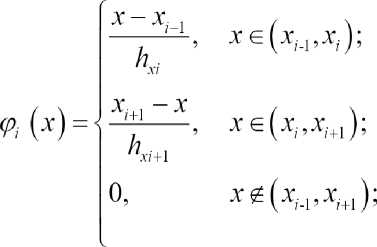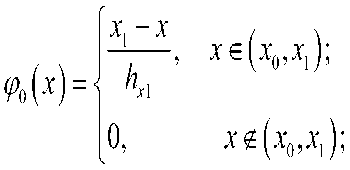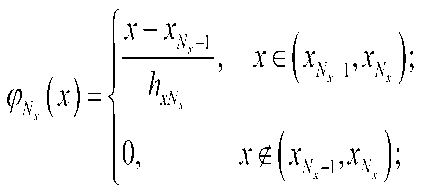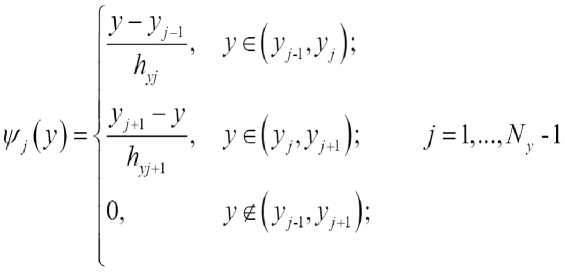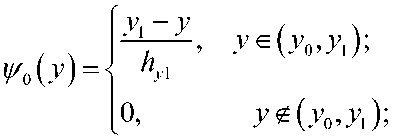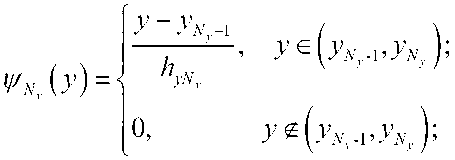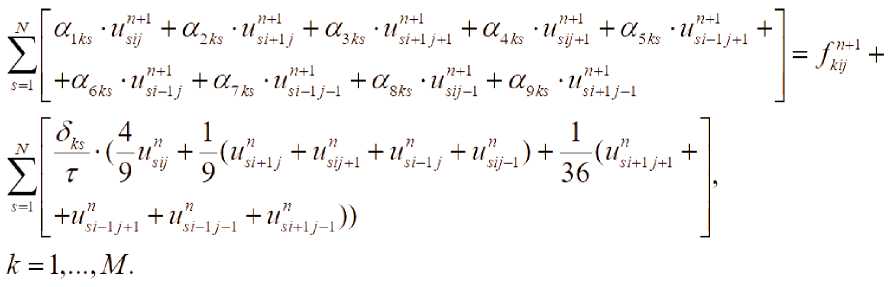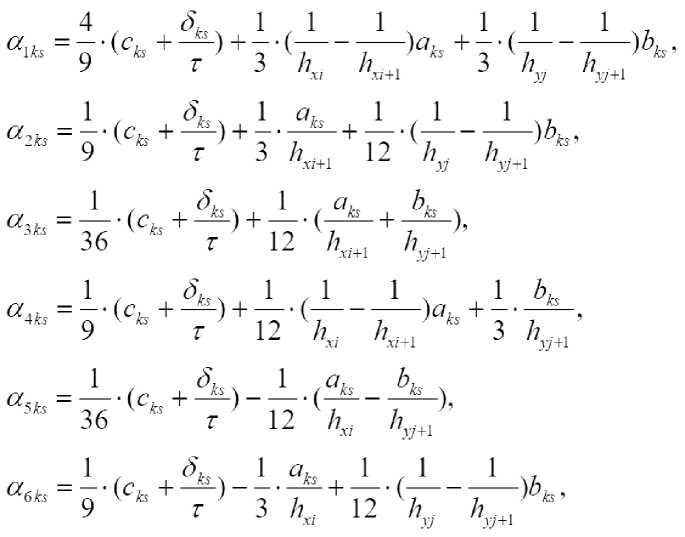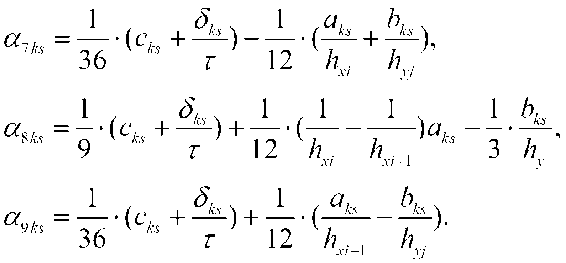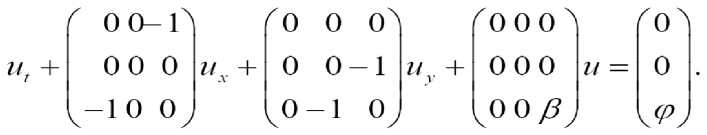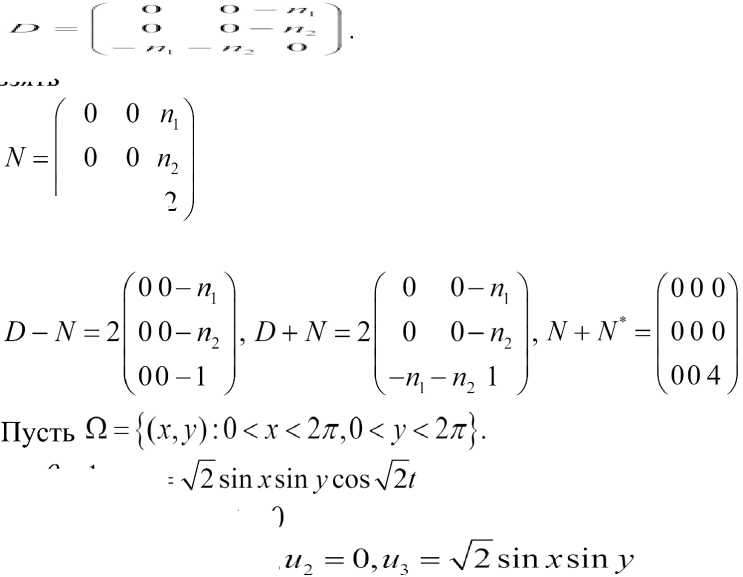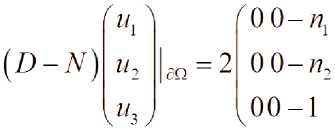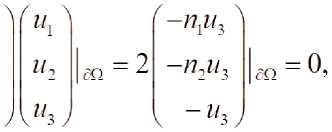Устойчивость неявной схемы конечных элементов для симметрических T-гиперболических систем

Автор: Давлатов Ш.О.

Статья в выпуске: 6 (87), 2024 года.

Бесплатный доступ

В этом статье рассмотрен метод конечных элементов для симметрических t-гиперболических систем. Создан алгоритм численного решения смешанной задачи для симметрических t-гиперболических систем методом конечных элементов на нерегулярной сетке. На основе этого алгоритма создана программа для численного решения смешанной задачи для симметрических t-гиперболических систем. Приведен численный расчет модельной задачи.

Метод конечных элементов, алгоритм, смешанная задача, гиперболическая система, базисные функции, неявно-разностная схема

Короткий адрес: https://sciup.org/140306437

IDR: 140306437

Текст научной статьи Устойчивость неявной схемы конечных элементов для симметрических T-гиперболических систем

1. Постановка задачи

В области Qr =Qx(O,r) рассматривается смешанная задача для симметрической t-гиперболической системы

Lu =-- h ^ A_t --h Bu = F ,

dt “^ dxt , с граничными условиями на :

(D-N)u = O

И с начальными данны ми при t = o u\_t=Q=g(x} ,

Здесь *^C ^JX^j ^ 3C^ } •

• •,^N) точка в пространстве /?N ,Q ограниченный область в

T?^N , ЦО) - граница области Q,XtX-^X z — 1,N симметрические матрицы размерностью m x m , элементы которых функции из CQO^DxC^Q) , B(t,x) матрица m x m , элементы которого функции из C^ , u(t₉xy = (z/₁(^,^),^z₂(/,Jv),...,w_/,₇(/,Jt)) неизвестная вектор функция, F(t,x) = (f^x^f^x^..^/"^^^¹ , /XteteX), i = \,m , g4X) = tetetegr₂(te---,^tey^v))⁷ , g,(teteX, i = Vm вектор функции . ^D=^M , W = (z7_|,...,Z7_n) внешний нормаль на границу области . N(t,x) матрица m x m , удовлетворяющая условию N + N*>0 и элементы которого непрерывные функции.

В Фридрихе[1] показана, что (1)-(3) смешанная задача при достаточных гладких условиях и следующих дополнительных предположениях

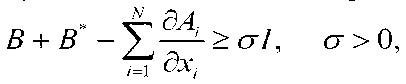
ker(D - TV) + ker(D + TV) = R^m на Г(О)х[0Х] имеет единственное решение. Здесь I единичная матрица.

2 Схема конечных элементов и ее устойчивость

Отрезок [OX] разобъем на X частей

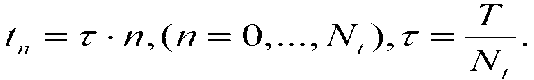
Проведем прямые x = x_j=hj (j = 0,...,N_x,h_x =-^-) , у = у j = Ki

(У O,..., TVy, Ay ) . Пересечение прямых x = xi и У^Уу, называемый узлом сетки, обозначим через .

Сетка разбивает прямоугольный область Q на части (элементы). Каждый элемент прямоугольник. Элементы, один из вершин которых, является узел Mg называются элементами этого узла. Объединение этих узлов обозначим через ^ij

Будем искать приближенное решение "At^y) на каждом слое t по времени в виде

“h = ¹А^^х’У) =EEx^-) • QS*^

i=Q ./=0

где Q^y) базисные функции, ^=^_i,y_jA„) = (u_li/(t_n),

■■•U.\!.

11 ll

Аппроксимируем систему (4) в узле My т.е. в системе (4) du производную по времени аппроксимируем отношением

u(t + T,x,y}-u(t,x,y} (< \ (. \

, вместо u[t,x,y) подставим "Ah^y) , каждое

T уравнение полученной системы умножим на Qu^y) и проинтегрируем по Qj . В итоге получим неявную разностную схему:

«,ej +v a^,q_u +о^а +r(c<ⁱ,ai =

=<^r‘.a)+(

В качестве примера базисной функции берем следующие функции Q_ij(x,y) = 0M-4'j(y), где

тогда после некоторых несложных вычислений из (5),

разностную схему

для системы (4) :

в узле

получим следующую

М.. = М(хс,у^Ек1_н,

1 если к = s

Здесь ^ks

О если кФ s’

Для того чтобы замкнуть систему линейных алгебраических уравнений (6) воспользуемся аппроксимациями граничных и начальных условий:

(D-^MZw+1,x,j/p|^

{D-N}u{t_n+vx,y^\_x=K =0

(£>-WW,,>’)|,.0 = 0 (7)

(D-N^t^x^y)_v4 =0

при :

u^O^^y^u^x^y^, Щх^у^Си. (8)

В качестве дополнительных граничных условий (неопределенных дифференциальной постановкой смешанной задачи) используется аппроксимация исходной системы. В итоге получим замкнутую систему линейных алгебраических уравнений. СЛАУ решим методом главных элементов.

Разобьем область Q на конечное число элементов(выпуклые многоугольники),не имеющих общих внутренних точек. Обозначим элемент через к . Тогда имеем ^ U . Отрезок [О, Г] делим на ■М частей. Точки

Т разбиения обозначим через.

Предположим, что выполняются следующее условии:

N + N*>Q,

В + В ^^ Лг — О.(10)

При таких предположениях справедлива следующая теорема.

Теорема. При выполнение условий (9)-(10) решение ^GWY’ однозначно определено на к и удовлетворяет неравенство

\\и„(1,х^ет\\и„(О^а + (Т+1\ет-ЦР .

Здесь14=(й, .

МО,И

Нерегулярная сетка создается следующим образом. Область Q разбиваем выше указанным способом на несколько частей. Это является первоначальной “грубой” сеткой. На этой сетке находим численное решение задачи (6)-(8). После нахождения решения, если модул разности значений , хотя бы одной компоненты вектор-функции u_hM , в узлах между Мд ,

^>0

то

м или в узлах между м,м больше заданного число i+] j J ’ середину этих узлов ставим новый узел. Создаем первую нерегулярную сетку. На этой сетке повторна находим численное решение задачи (6)-(8). Аналогично выше указанным способом создаем следующую нерегулярную сетку. Этот процесс будем повторять пока не будет выпольнятся неравенства Uki+\J ~Ukij -^ и .

3 Численные расчеты

Задача.

В области G = ^t^x^: / g (О,Г), (x, y) g Qj дано уравнение затухающий волны

4 + /4 - ww - w^ = y>,/? > 0

w, wr заданы при / = 0

w = 0 на dQ .

Вводя обозначении получим следующую систему и, = w.m = w.ii, = w.

В этом задаче

Если взять

то тогда

-w, - w2 2

Возмем 0^— 1иФ ⁼начальные условии при t = 0 = 0,

условие на границе

Из этого следует, что на всей стороне прямоугольника .

При t>0 точное решение смешанной задачи будет ъу = cos x sin у sin X^t ji2 =sinxcosyshi \/2y iy = л/2 sin x sin у cos y/2t .

В таблице ниже приведены значения разницы \\u 1

13X1) на

неравномерной сетке при различных разбиениях по времени t и первоначальном разбиении N_x=3,N_y=3 по X и по у соответственно, при J = 0,2 и при .

	N_x		ll"~^vL_IQ1
10	13	13	0.4603349
20	13	13	0.2622136
40	13	13	0.1154079
80	13	13	0.0228676

160

0.0220265

Список литературы Устойчивость неявной схемы конечных элементов для симметрических T-гиперболических систем

K. O. Friedrichs, Symmetric positive linear di erential equations, Comm. Pure Appl. Math.,11 (1958), pp. 333-418.
L. J. Segerlind.Applied Finite Element Analysis. John Wiley & Sons, Inc. 1976.pp. 289-308.
R.D. Aloev, Z.K. Eshkuvatov, Sh.O. Davlatov, N.M.A. NikLong. Sufficient condition of stability of finite element method for symmetric T-hyperbolic systems with constant coefficients.Computers and Mathematics with Applications. USA.68(2014) рр. 1194-1204. (Scopus. IF=3.37).

Статья научная