Устойчивость нелинейно-упругой пластины при боковом сжатии
Автор: Волокитин Г. И.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 2 т.20, 2020 года.
Бесплатный доступ
Введение. Если круглая пластина нагружена по боковой поверхности, возможны потеря ее устойчивости и выпучивание. Данную проблему можно решить с учетом бифуркации. В этом случае пластина рассматривается как нелинейно-упругое тело. В задачах устойчивости нелинейной упругости важен выбор зависимости между напряжениями и деформациями. В ранних работах, посвященных этой проблеме, рассматривались простые законы состояния (конститутивные уравнения). В качестве примера можно привести материал «гармонического типа» Сенсенига.Материалы и методы. Для круглой пластины из материалов Мурнагана и Блейтца и Ко получены уравнения нейтрального равновесия. В предположении однородной начальной деформации рассмотрена задача устойчивости этой пластины. Строгие трехмерные уравнения нейтрального равновесия позволяют исследовать смежные формы равновесия с учетом физической и геометрической нелинейности. Вывод этих уравнений основан на теории наложения малой деформации на конечную.Результаты исследования...
Конечная деформация, напряжения, выпучивание, пластина, устойчивость
Короткий адрес: https://sciup.org/142223730
IDR: 142223730 | УДК: 519.6 | DOI: 10.23947/1992-5980-2020-20-2-137-142
Текст научной статьи Устойчивость нелинейно-упругой пластины при боковом сжатии
УДК 519.6
Stability of a nonlinear elastic plate under lateral compression
Don State Technical University (Rostov-on-Don, Russian Federation)
Introduction. Loss of stability and buckling of a round plate may be observed if the plate is loaded on the lateral surface. The solution to this problem is based on a bifurcation approach. In this case, a plate is considered as a nonlinear elastic body. It is important to choose the relation between stresses and deformations in sustainability problems of nonlinear elasticity. Simple laws of state (constitutive equations) were considered in early works devoted to this problem, for example, material of the “harmonic type” (Sensenig).
Materials and Methods . Equations of neutral equilibrium for round plates made of Murnaghan and Blatz-Ko materials are obtained. Assuming a uniform initial deformation on the plate, the stability problem is considered. Strict threedimensional neutral equilibrium equations provide exploring related forms of equilibrium taking into account physical and geometric nonlinearity. Derivation of these equations is based on the application of the theory of superposition of small deformation on the final one.
Механика
Results. Progress in solution to the corresponding secular equation (with non-linear parameter entry) for practically important laws of elasticity of Murnaghan and Blatz-Ko is possible using the numerical methods only. The developed method for calculating bifurcation values of loading parameters makes it possible to analyze the effect of nonlinearity. Discussion and Conclusions. The influence of physical and geometric nonlinearity on the upper critical value of the initial deformation parameter is explored. The results obtained can be used under the assessment of reliability of elastic third-order moduli for various physical materials. Data on these moduli is still scarce. The numerical research has shown that the constants given in some sources should be treated with caution. The use of elasticity moduli in the law of state of Blatz-Ko is also discussed.
Введение. В настоящее время изучение новых сравнительно простых и адекватных законов состояния различных материалов, требующих учета нелинейных деформаций, представляет собой активно развивающееся направление механики сплошной среды [1–10]. В рамках теории наложения малой деформации на конечную выведены трехмерные уравнения нейтрального равновесия для материалов Мурнагана и Блейтца и Ко. На основе этих уравнений рассмотрен пример торцевого выпучивания равномерно сжатой круглой пластины [11, 12].
Материалы и методы
Уравнения нейтрального равновесия. Пусть r , φ , z — цилиндрические координаты точки в недеформированном состоянии. Предполагаем, что начальная деформация тела определяется радиус-вектором R :
R = R ( r ) er + dzi3 , (1)
где R ( r ) = ar , параметры a , d — константы, e r , e ф , i 3 — базисные векторы.
Для координат этой точки в начально-деформированном состоянии имеем:
R = ar , Ф = ф , Z = dz .
Следовательно, градиент деформации, мера деформации Фингера и ее главные инварианты определены соотношениями:
V R = V RT = a ( erer + е ф e ф ) + di 3 i 3 , F = V R 2,
I 1 = 2 a 2 + d 2, 1 2 = a 4 + 2 a 2 d 2, 1 3 = a4 d 2. (2)
Здесь и далее V , V — набла-оператор в метрике недеформированного и начально-деформированного состояния: V = V R -V .
Будем использовать уравнения нейтрального равновесия, предложенные А. И. Лурье [13]: V 0 = 0, где тензор Θ — линейный дифференциальный оператор над вектором добавочных перемещений w . Выражения компонент этого тензора, конкретизированные с учетом законов состояния Мурнагана и Блейтца и Ко, получены в работах [14, 15]. В представлениях тензора Θ компоненты — некоторые функции, определяемые в результате решения краевой задачи начальной деформации.
Результаты исследования. Для рассмотрения изгибной формы бифуркации равновесия пластины аналогично работам [11, 12] принимаем следующий вектор добавочного перемещения
W = u(r, z)er + w(r, z)i3.(3)
Учитывая (1), (2) и (3), тензор Лурье имеет вид:
0 = Aerer + Be ф e ф + Ci 3 i 3 + Gi 3 er + He r i3 .
Здесь . . u . du . dw u du dw _ _ u _ ди _d
A = A + A + A , B = B- + B + B , C = C + C3+
12 3 12 3 123
r dr dz r dr dz r dr
G = G , ^ u + G, ^w , H = H ^ u + H ? w
1 dz 2 dr 1 dzd
Отметим, что структура этих операторов типична в задачах устойчивости цилиндрических нелинейноупругих тел. Опуская выражения остальных коэффициентов, приведем, например, формулы для A 1 . В случае закона состояния Мурнагана [13, 14] A 1 выражается соотношением
Л a I 1
A = X
1 d I
—
3 v 1 + 4 v 2
+ V 1 d 2 + ( v 1 + 2 v 2) aг
Здесь и далее λ и μ — модули упругости Ляме, ν 1 , ν 2 , ν 3 — константы упругости третьего порядка. Для материала Блейтца и Ко [15]:
_ 2 Ц (1 -в ) ( . 2 в 2 / 2 , )
A1 = г- \ I 3 + I 3 I , a^I3 к 1 — в )
где β — уточняющий модуль упругости.
Уравнение нейтрального равновесия равносильно системе дифференциальных уравнений относительно
компонент вектора w :
. (д2и 1 дu и । ( . a „ ) д2 w a „ д2и
A2I—- + - - I + I A3 + G2 I----+ G.—- к д r2 r д r r2 ) к d ) д r дz d дz2
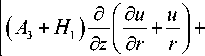
( д 2 w 1 д w ) a д 2 w „
H2I—2" +--I+ C3—г = 0.
к д r2 r д r ) d дz2
Предполагая, что по боковой поверхности пластина нагружена равномерным давлением, дифференциальные уравнения (4) дополним условиями равновесия на границе:
и ( r , z )|r_r = 0, ® rzV г = 0. ' r H ' r H
На торцах, т. е. при
z = ± 2 0 zr = 0, 0 zz = 0.
Применим подстановку
и = X n ( z ) J . ( k n r ), w = Z n ( z ) J 0( k n r ).
Здесь n = 1, 2, .. , J 0, J , — функции Бесселя нулевого и первого порядка, а числа knrH — нули функции J 1 ( x ).
Примем x = knr и применим равенства
dJ 1( knr ) d 2 J 1( k n r )
= k n J 1( x ), dr dr 2
а также известные тождества для функций Бесселя 11
u 1 + 1 1
xx 2
= k n J ГС x ),
dJ 0( k n r ) = k n J 0 ( x ) =- k n J ‘ ( x ), dr
1 , 0
+ и0 ^0 .
x
Выполнив перечисленные выше действия, получим, что переменные в дифференциальных уравнениях (4) и граничных условиях (5) разделяются. Приходим к следующей краевой задаче для обыкновенных дифференциальных уравнений:
—
n
k n 2 A 2 X n
—
k n G^C Z n = 0,
<
Z ‘ — k2 G 1 Z + k„ G 2 + C 2 X' = 0. nn nn n
k n C 1 X n ( ± h( 2 ) + C з Z n ( ± hl 2 ) = 0, k n G 2 Z n ( ± h /2) — G 1 X n ( ± h /2) = 0.
Два однородных линейных обыкновенных дифференциальных уравнения (7) и четыре краевых условия (8) приводят к задаче на собственные значения с нелинейным вхождением параметра. В данной задаче таким параметром является величина ( 1 — a ) . Систему (7) приведем к нормальному виду:
' y‘ = y 2, y‘ = kn”2" y + k, Z 2 n H2 71 '
y 3 = y4, y 4 = kn. Gr y 3— kn
. C 3
<
+
22 y 4,
G 1
+
22 y 2.
Здесь приняты обозначения: аргумент
t = z ,
фундаментальная система решений — это следующие
четыре
( У 1 ; y 2 ; y 3 ; y 4 ) T = ( X n ; X n ; Z n ; Z n ) T . Пусть вектора y i = ( y1i ; y2i ; y3i ; y 4 i ) T . Тогда общее
Механика
решение системы имеет вид ( Xn ; X n ; Zn ; Z n ) Tобщ
= Z ^,y,, где i =1
ξi — произвольные постоянные. Зададим,
например, при z = — h /2 начальные данные столбцами единичной матрицы четвертого порядка. Затем решим
численно задачу Коши с этими начальными условиями. В результате в правой части получим значения базисных функций, то есть векторы y^ ( + h /2). Используя граничные условия (8), приходим к однородной системе линейных алгебраических уравнений относительно i l , i 2, i 3, i 4:
f a j i j = 0, где i = 1, 2, 3, 4. j = 1
Здесь коэффициенты — элементы матрицы A :
aij = kCУи (-h/2) + C3У4j(-hl2), a2j = kCУ^ (hl2) + C3У4j (hl2), a3j = k„G2У3j (-h/2) - GУ2j (-h2), a4j = k„G2У3j (h2) - GУ2j (hl2).
Однородная система имеет нетривиальное решение, если выполнено условие det A = 0 . (9)
Выражение определителя включает параметры нагрузки a , d , нули функции Бесселя, а также модули упругости X , ц , v i, v 2, v 3 (для материала Мурнагана) либо X , ц , р (для материала БлейтцаиКо).
Параметры a , d , задающие начальную деформацию, взаимосвязаны. Осевая сила, действующая на
Rн площадку поперечного сечения, определяется соотношением [13]: Q = 2п j aZ RdR , где aZ — физическая 0
компонента тензора напряжений. Поскольку начальная деформация предполагается в виде (1), то тензор напряжения Коши T и мера деформации Фингера F соосны. Причем тензор напряжений — постоянный:
T = ad ( c <0) ( a 2( ее + е ф е ф ) + d 2 i 3 i 3 ) - с (i) ( a 4( ее + e ф e ф ) + d4 i 3 i 3 ) + c ( - I) ( ее + e ф e ф + i 3 i 3 ) ) .
Торцы пластины свободны от нагрузки, поэтому а Z = 0. Отсюда следует условие, связывающее коэффициенты закона Фингера
( - 1 )
c (0) - c (1) d2 + c ^ = 0. (10)
Принимая во внимание закон состояния, можно записать конкретное выражение условия (10), которое устанавливает связь между a и d. Так, для материала Мурнагана получаем условие:
^V- + ^ V 1 + 2 v 3 ^ d 4 +^ X + 2 ц - ^L - 5 v 2 - 4 v 3 + ( v i + 2 v 2) a 2 ^ d 2 -
-
- 3Х - 2p + ^1 + 2 V 1 + V 3 + (2X - 3 v L - 4 v 2 - ^1 ) a 2 + ( v L + v 2 - ^1 ) a4 = 0.
В частности, если v L = v 2 = v 3 = 0 , то имеем
-
2 2X 2\
d = 1 +-- 11 - a ).
-
X + 2p
При рассмотрении закона состояния Блейтца и Ко d выражается формулой d = a "2/3.
Таким образом, задавая значения модулей упругости, нули функции Бесселя, из (9) находим бифуркационные значения параметра начальной деформации a , .
Отметим, величина Л = 1 - a , для сравнительно тонких дисков — малый параметр. Так, в классической теории выпучивания пластин критическое значение величины a , определяется формулой
, (3,8317)2 f h ] a. = 1 - ,
12(1 + v) ( Гн J
где v — коэффициент Пуассона, а 3,8317 — первый корень функции Бесселя J , ( x ).
При решении начальной краевой задачи предполагается возможность применения метода возмущений Синьорини. При этом считаем, что коэффициенты оператора 0 зависят от малого параметра Л степенным образом. Это означает, что условия на границе для компонент добавочного перемещения задаются Л матрицей A = A ( Л ). В данной задаче имеет физический смысл частичная проблема собственных значений — определение низших собственных чисел. Старшие степени Л , которые содержат элементы матрицы A , незначительно сказываются на значениях наименьших корней векового уравнения (9). Если при решении начальной задачи ограничиться линейной теорией, то A ( Л ) — регулярный двучлен [16].
Численные эксперименты при исследовании устойчивости нелинейно-упругих тел не слишком большой относительной толщины подтверждают этот вывод. Следовательно, характеристическое уравнение с нелинейным вхождением параметра (9) можно заменить характеристическим уравнением линейного оператора.
Можно применить итерационные процессы, сходящиеся к одному собственному числу, где в качестве нулевого приближения выбиралось число, близкое к значению в теории пластин.
Обсуждение и заключение. С помощью полученных выше уравнений выполнен численный анализ влияния физической и геометрической нелинейности на величину верхнего критического значения параметра a , . Расчеты реализованы в среде Matlab для различных вариантов задания модулей упругости, относительной толщины пластины и числа волнообразования n . Обнаружено, что во всех случаях потери устойчивости диска минимальному критическому значению параметра a , отвечает первая форма выпучивания, которая соответствует корню функции Бесселя 3,8317 [17].
В табл. 1 приведены критические значения параметра a , для пластин относительной толщины 0,05; 0,1; 0,15; 0,2; 0,25 и 0,3.
Таблица 1
Критические значения параметра a , для пластин различной относительной толщины
|
hrн |
Относительная толщина пластины |
|||||
|
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
|
|
1 |
0,9922 |
0,9869 |
0,9800 |
0,9660 |
0,9530 |
0,9330 |
|
0,9972 |
0,9867 |
0,9735 |
0,9549 |
0,9300 |
0,8914 |
|
|
2 |
0,9977 |
0,9908 |
0,9801 |
0,9664 |
0,9504 |
0,9332 |
|
0,9967 |
0,9869 |
0,9690 |
0,9410 |
— |
— |
|
|
3 |
0,9976 |
0,9907 |
0,9800 |
0,9662 |
0,9502 |
0,9330 |
|
0,9965 |
0,9856 |
0,9665 |
0,9372 |
— |
— |
|
|
4 |
0,9977 |
0,9907 |
0,9798 |
0,9659 |
0,9497 |
0,9324 |
|
0,9881 |
— |
— |
0,9965 |
0,9613 |
0,9861 |
|
|
5 |
0,9914 |
0,9865 |
0,9783 |
0,9668 |
0,9520 |
0,9350 |
|
0,9929 |
0,9729 |
0,9341 |
0,9114 |
— |
— |
|
|
6 |
0,9978 |
0,9912 |
0,9800 |
0,9675 |
0,9520 |
0,9340 |
|
0,9985 |
0,9941 |
0,9871 |
0,9775 |
0,9651 |
0,9539 |
|
|
7 |
0,9985 |
0,9941 |
0,9859 |
0,9735 |
0,9560 |
0,9320 |
|
0,9985 |
0,9941 |
0,9863 |
0,9749 |
0,9594 |
0,9396 |
|
Здесь цифрами обозначены перечисленные ниже материалы.
-
1. Сталь Rex 535 (X = 1,09, ц = 0,818 , v 1 =- 1,75, v 2 =- 2,40, v 3 =- 1,69).
-
2. Сталь 50ХГСМ2Ф (X = 1,129, ц = 0,803, v 1 =- 2,8, v 2 =- 2,7, v 3 =- 1,87).
-
3. Сталь Hecla 37 ( X = 1,11, ц = 0,821, v 1 =- 3,58, v 2 =- 2,82, v 3 =- 1,77 ).
-
4. Сталь Hecla ATV ( X = 0,87, ц =0,716, v , = 0,34, v 2 =- 5,52, v 3 =- 1,0 ).
-
5. Бронза бериллиевая (X = 1,042, ц = 0,49, v , =- 4,0, v 2 =- 1,7, v 3 =- 0,6).
-
6. Оргстекло (X=0,39, ц = 0,186, v , =- 0,078, v 2 =- 0,07, v 3 = 0,047).
В первых шести вариантах рассмотрен закон состояния Мурнагана. Последний вариант представляет результаты для материала Блейтца и Ко. Верхнее число в ячейке таблицы относится к случаю, в котором не учитывается физическая нелинейность, т. е. v 1 = v 2 = v 3 = 0 в законе Мурнагана; в = 0 в законе Блейтца и Ко. Второе (нижнее) число учитывает физическую нелинейность. В законе Мурнагана были использованы данные дин для модулей упругости третьего порядка из [14] в единицах 1012 .
см 2
В последней строке табл. 1 приведены результаты для закона Блейтца и Ко, который выбран в упрощенном варианте (уравнение Ноулса — Стернберга): коэффициент Пуассона принимался равным 0,25, а уточняющий модуль в = 0,45. Прочерк означает, что критическое значение a , не обнаружено.
Механика
Анализ результатов позволяет сделать некоторые выводы. При малых относительных толщинах диска точная теория и линейная теория пластин дают одинаковые критические значения параметра a,. Геометрическая нелинейность заметно влияет при относительных толщинах больше 0,1. Еще сильнее сказывается физическая нелинейность. Однако следует с осторожностью выбирать значения упругих модулей третьего порядка. Например, в четвертом варианте (сталь Hecla ATV) и для тонких пластин не были обнаружены надежные критические значения параметра a∗ , хотя для тех же значений модулей упругости Ляме наблюдаются приемлемые значения, свидетельствующие о потере устойчивости. Как и в задаче устойчивости нелинейно-упругой сферы из материала Блейтца и Ко [15], константа β слабо влияет на величину критического значения a .
∗
Список литературы Устойчивость нелинейно-упругой пластины при боковом сжатии
- Azarov, A. D. Description of non-linear viscoelastic deformations by the 3D mechanical model/ A. D. Azarov, D. A. Azarov // Physics, Mechanics of New Materials and Their Applications : proc. of the International Conference, devoted to the 100th Anniversary of the Southern Federal University / Eds. Ivan A. Parinov, Shun-Hsyung, Vitaly Yu. Topolov. - New York : Nova Science Publishers. - 2016. - Ch. 49. - P. 367-375.
- Азаров, Д. А. Механико-геометрическое моделирование в нелинейной теории упругости / Д. А. Азаров, Л. М. Зубов // Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки.-2016. - № 3(191).-С.5-12.
- Калашников, В. В. Использование модели материала Мурнагана в задаче плоского изгиба упругого стержня/ В.В.Калашников, М. И. Карякин // Труды Ростовского государственного университета путей сообщения. -2006. -№2(3). - С.56-65.
- Роговой, А.А. Определяющие соотношения для конечных упруго-неупругих деформаций / A.А. Роговой// Прикладная механика и техническая физика.-2005.- Т.46, №5. -C. 138-149.
- Aidy, A. A Review of Constitutive Models for Rubber-Like Materials / A.Aidy, M.Hosseini, B.B. Sahari // American Journal of Engineering and Applied Sciences. - 2010. -№3(1).-P.232-239.
- Gent, A. N. Engineering with rubber / A. N. Gent. - Munchen: Carl Hanser Verlag & Co. KG, 2012. - P.451.
- Greaves, G. N. Poisson's ratio and modern materials / G. N. Greaves, A. L. Greer, R.S.Lakes, T.Rouxel// Nature Materials. -2011. - № 10. -P.823-837.
- Marckmann, G. Comparison of hyperelastic models for rubber-like materials /, G. Marckmann, E.Verron// Rubber Chemistry and Technology, American Chemical Society. -2006. -№79(5). -P.835-858.
- Азаров, А. Д. Трехмерная механическая модель для описания больших упругих деформаций при одноосном растяжении / А.Д.Азаров, Д.А. Азаров// Вестник Донского государственного технического университета.-2011. -Т.11, №2(53). - С.147-156.
- Еремеев, В. А. Механика упругих оболочек / В. А. Еремеев, Л.М.Зубов. - Москва: Наука, 2008. -280с.
- Sensenig,C.B. Instability of thick elastic solids / C.B.Sensenig// Communications on pure and applied mathematics. - 1964. -Vol.XVII.-P.451-491.
- Зубов, Л. М. Выпучивание пластинок из неогуковского материала при аффинной начальной деформации / Л. М. Зубов // Прикладная математика и механика.-1970.-Т.34, вып.4.-С.632-642.
- Лурье, А.И. Нелинейная теория упругости /А. И. Лурье. - Москва: Наука, 1980. - 5 12 с.
- Волокитин, Г. И. Устойчивость нелинейно-упругого цилиндра при боковом давлении и осевом сжатии/ Г.И.Волокитин//Прикладная математика и механика.-1982.- Т.42, вып.2. -С.289-295.
- Волокитин, Г. И. Условия бифуркации равновесия сферы / Г.И.Волокитин, Д.В.Моисеев// Современные проблемы механики сплошной среды: тр. XV междунар. конф. - Ростов-на-Дону: Изд-во ЮФУ, 2011. -Т.1. - С.69-73.
- Гантмахер, Ф.Р. Теория матриц / Ф.Р. Гантмахер. -Москва: Наука, 1968. -576с.
- Янке, Е. Специальные функции / Е. Янке, Ф. Эмде, Ф. Лёш.-Москва: Наука, 1968. - 3 52 с.


