Устойчивость ортотропной пластины с двумя свободными краями, нагруженной изгибающим моментом в плоскости

Задача устойчивости прямоугольной пластины, нагруженной по двум противоположным краям усилиями, распределенными по линейному закону, впервые была решена для изотропной пластины И. Г. Бубновым [1] и С. П. Тимошенко [2]. Для ортотропной пластины эта задача была впервые сформулирована и решена С. Г. Лех-ницким [3]. Эти классические решения были получены для случая шарнирного закрепления краев пластины в форме двойных тригонометрических рядов. Для определения критического усилия в этих решениях был использован энергетический метод Ритца. Это связано с тем, что дифференциальное уравнение устойчивости пластины имеет переменный коэффициент и поэтому его интегрирование оказывается затруднительным. Метод Ритца был также использован в [4] и [5] для решения рассматриваемой нами задачи применительно к композитным пластинам с шарнирно закрепленными краями, которые нагружены равномерными сжимающими усилиями.

Таким образом, можно утверждать, что устойчивость пластины при изгибе в плоскости наиболее полно исследована только для самого распространенного вида граничных условий – шарнирного закрепления сторон. Это подтверждает и тот факт, что в справочнике [6] имеется всего одна ссылка на статью К. Нолке [7], в которой рассматриваемая задача решена для пластины с двумя защемленными продольными краями.

Авторами решена задача устойчивости при чистом изгибе ортотропной пластины, у которой два противоположных края свободны, а два других края шарнирно закреплены. Отметим, что для таких граничных условий задача о выпучивании ортотропной пластины при действии сил, линейно распределенных по краям, до настоящего времени не исследована. Задача устойчивости ортотропной пластины для аналогичных граничных условий решена лишь для пластины, нагруженной по краям только равномерными сжимающими усилиями [8].

В данной статье решение исходного уравнения устойчивости разыскивалось в форме Леви. Это позволило свести разрешающее уравнение в частных производных к обыкновенному однородному дифференциальному уравнению, для решения которого использовался метод конечных разностей. В результате была получена однородная система линейных алгебраических уравнений, аппроксимирующая краевую задачу. Задача определения критического усилия была сведена к вычислению безразмерного коэффициента устойчивости, значение которого соответствовало минимальному собственному числу однородной системы уравнений. Также были решены задачи устойчивости для изотропной пластины и симметрично армированной ортотропной пластины и выполнен анализ влияния геометрических и упругих параметров пластины на величину коэффициента устойчивости и на характер волнообразования при выпучивании.

Решение уравнения устойчивости. Рассмотрим ортотропную пластину, срединная плоскость которой отне сена к декартовым координатам xy (см. рисунок) . Обозначим через a и b размеры пластины по осям x и y соответственно. Два противоположных края пластины y = 0 и y = b свободны, а два других края x = 0 и x = a шарнирно закреплены. По закрепленным краям пластина нагружена нормальными усилиями, изменяющимися по линейному закону. Распределение усилий на краях соответствует двум изгибающим моментам, действующим в плоскости пластины.

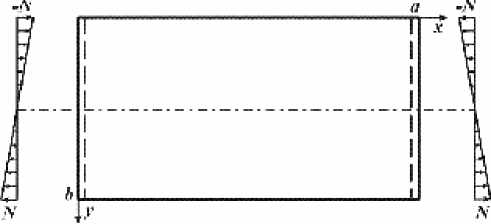
Нагружение пластины

Классическое уравнение устойчивости для ортотроп-

ной пластины имеет вид

D11 . . + 2 ( D12 + 2 D33 )—ГТТ + D 22 dx               dx dy d4 w dy4

- N    — 2 NL--No    = 0, x dx2      xy dxdy     y Вy y где w = w(x, y) – прогиб пластины; D11, D12, D22, D33 – изгиб-ные жесткости пластины, приведенные в [9]; Nxo,Noy,Nxoy – мембранные усилия, соответствующие докритическо- му состоянию пластины.

Будем считать, что исходное напряженное состояние пластины соответствует ее чистому изгибу в плоскости xy. Тогда мембранные докритические усилия могут быть определены следующим образом:

N O = - N ( 1 - 2 y ) , N; = 0, N y = 0,       (2)

I b )

где N – значение максимального усилия на краях y = 0, y = b .

С учетом равенств (2) уравнение устойчивости (1) примет вид

D,, —— + 2( D„ + 2 D J d , +

• ¹¹    d x^{4                 33} d x ²d y²

+ D 22 ^ — + N | 1 - 2 y l^- T = 0.         (3)

²² d y ⁴      I      b ) d x ²

Рассмотрим граничные условия. На шарнирно закрепленных краях x = 0 и x = a прогибы пластины и изгибающие моменты равны нулю. На свободных краях пластины y = 0 и y = b должны отсутствовать изгибающие моменты и обобщенные перерезывающие силы [9]. Эти граничные условия могут быть записаны через прогиб пластины w. Для краев с шарнирными опорами при x = 0 и x = a будем иметь d2w     d2w л

N = 0, Dii ^TN + D12     =0- dx

На свободных краях при y = 0 и y = b граничные усло- вия можно записать в виде d2 w d2 w

12---7" + D22= 0 5

• 12    dx2      22 ay2’

D^    + (Dn + 4 D 3)   ---= 0.(5)

a y               a x a y

Таким образом, задача устойчивости пластины сводится к определению параметра N, при котором однородная краевая задача (3), (4) и (5) будет иметь решение, отличное от нуля.

Шарнирное закрепление краев x = 0 и x = a допускает представление решения уравнения (3) в форме Леви, т. е. в виде одинарного тригонометрического ряда

• — ⁽ x , y ) = j^ — m ⁽ y ) sin x m x ,             (6)

m =1

где m – число полуволн вдоль стороны a ; w _m ( y ) – неизвестная функция; X m = m п / a . Однако в рассматриваемой нами задаче нет необходимости аппроксимировать прогиб пластины в направлении оси x рядом (6). Вполне достаточно удержать в нем один, первый член с m = 1 . На самом деле, при выпучивании пластины ее свободные края не испытывают никакого стеснения. Поэтому искривление пластины всегда происходит с образованием одной полуволны вдоль стороны а. Эта полуволна на краю y = 0, где N _x ^o = – N , имеет максимальную амплитуду, которая уменьшается к краю y = b.

Все вышесказанное позволяет представить решение уравнения (3) в виде

• — ( x , y ) = w ( y )sin X x ,                  (7)

где w ( y ) = w ₁( y ); l = п / a .

Подставляя (7) в (3), получим обыкновенное однородное дифференциальное уравнение

Di ,X2 w — 2(D12 + 2 D33)—— + 111233

dy ²

+ D22- d-w — N f1 — 2 y) w = 0.(8)

X ² dy ⁴

Здесь и далее w = w ( y ). Подставляя (7) в граничные условия (5), при y = 0 и y = b будем иметь

D12X2 w—D22 dw = 0,(9)

dy ²

—D22 dw + (D12 + 4 D33)X2 dw = 0.(10)

dy3

Для решения уравнения (8) воспользуемся методом конечных разностей. Разобьем сторону пластины b на n равных частей. Обозначим через s шаг разбиения. Тогда s = b/n. Точки разбиения имеют координаты y = 5(i — 1),      i = 1,2,..., k,           (11)

где k = n + 1.

Для произвольной i- й точки аппроксимируем производные, входящие в (8), (9) и (10), следующими конечноразностными соотношениями:

^f dw )    1 /           ,

=   (— w + w^ )

7                                — 1          I + 1 , dy2s i

Nb ²

D ₁₁ D ₂₂

здесь n — безразмерный коэффициент устойчивости.

Записывая уравнение (15) для всех точек i = 1, 2, …, k , получим однородную систему линейных алгебраических уравнений, которая наряду с неизвестными w ₁, w ₂, …, w _k будет содержать также неизвестные в законтурных точках.

Покажем место законтурных неизвестных в структуре системы уравнений. Из уравнения (15) следует, что для этого необходимо определить разностные соотношения A _i и B _i на краях пластины y = 0 и y = b. Положим последовательно в равенствах (14) i = 1 и i = k . Тогда

A = w ₀ — 2 w ₁ + w ₂,

B ₁ = w _{— 1} — 4 w ₀ + 6 w ₁ — 4 w ₂ + w ₃         (18)

и

A = w k ■ ^{— 2} w k ⁺ w k +1 ,

^Bk = w k —2 ^{— 4} w k ■ ^{+ 6} w k ^{— 4} w k +1 ⁺ w k +2 .      ⁽¹⁹⁾

Таким образом, законтурными неизвестными являются w _–1, w ₀, w _{k +1}, w _{k +2}. Отметим, что неизвестные w ₀ и w _{k +1} также будут входить в разностные соотношения B ₂ и B _{k –1}:

B 2 = w 0 — 4 w ₁ + 6 w ₂ — 4 w ₃ + w ₄ ,

B k ■ = ^wk —3 ^{— 4 w}k —2 ^{+ 6 w}k ■ ^{— 4} w k ^{+ w}k +1 .    ⁽²⁰⁾

d w )    1 z           .

I = "Г ⁽ w —1 ^{— 2} w i ⁺ w +1 ), dy J, 5

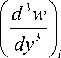
= —r(^_ w 2 + 2 w, 1 i 2                i 1

2 s ³

^{— 2} w i +1 ⁺ w i+ 2 ),

f d ⁴ w I 1 Z Л             Л X

I "TV I = — ^{( w}i —2 ^{— 4 w}i —1 ^{+ 6} w i ^{— 4} w i +1 ⁺ w i +2 X

( dy ) _i 5

где w _i = w ( y _i ).

Используя равенства (12), запишем для i- й точки

ко-

Для определения четырех законтурных неизвестных необходимы четыре уравнения, которые можно получить с помощью конечно-разностной аппроксимации граничных условий (9) и (10). Заменяя производные в равенстве (9) конечно-разностными соотношениями (12) при i = 1 и i = k , будем иметь

2 n ²

Р ₁ п w ₁--( w ₀ — 2 w ₁ + w ₂) = 0

а

2 n ²

Р 1 ^{п w}k --^{( w}k ■ ^{— 2 w}k ^{+ w}k +1 ) = ⁰,       ⁽²¹⁾

а

нечно-разностную аппроксимацию дифференциального уравнения (8):

2     ~ D 2 + 2 D₃₃

D11X2 w — 2 12 2 33 4 + s2

где

P = ____

^{1      D} 11 ^D 22 ^.

Из уравнений (21) найдем

+ D r Bi — N 1 1 — 2 y I w = 0, X ² 5 ^{4 i} I b J

где A _i и B _i – разностные соотношения, которые имеют следующий вид:

A = w —1 ^{— 2} w i + w i +1 ,

B i = w i —2 ^{— 4} w i —1 ^{+ 6} w i ^{— 4} w i +1 ⁺ w i+ 2 .

Для удобства дальнейшего анализа преобразуем уравнение (13) к уравнению с безразмерными коэффициентами. Учитывая выражение (11) и равенства X = п / a , 5 = b / n , из (13) будем иметь

22 ^{n 4}

ап ² w _i — 2 р n ² 4 + — у B _i —П t _i w _i = 0,     (15)

ап

w 0 = ⁽ Г 1 ^{+ 2)} w 1 ^— w 2 , w k +1 = ^{( r} 1 ^{+ 2) w}k ^{— w}k ■ , ⁽²³⁾ где r ₁ = аР ₁ п ² / n ² .

Для определения w—1 и wk+2 аппроксимируем производные в равенстве (10) разностными формулами (12). Подставляя (12) в (10) при i = 1 и i = k, получим n2

--^{( — w} —1 ^{+ 2 w} 0 ^{— 2 w} 2 ^{+ w} 3 ) ⁺ а

+(P1 + 4Р2)п2(—w0 + w2) = 0, n2                                        (24)

--^{( — w}k 2 ^{+ 2 w}k —1 ^{— 2 w}k +1 ^{+ w}k +2 ) ⁺ а

+ ( P 1 + 4 Р 2 ) п ² ( — w k —1 + w k +1 ) = 0,

где t _i = 1 – 2( i – 1)/ n ;

I D u b²    0    D 12 ^{+ 2 D} 33 .

а = x-- 2 ; ^e = — 1        ;

^D 22 ^{a          D} 11 ^D 22

где p2 =   D33    .

D ₁₁ D ₂₂

Учитывая (23), из (24) найдем

^W -i = (2 + r i + ⁴ r 2⁾⁽ r + 2) - -

- 2(2 + г , + 4 r ₂) w ₂ + w₃ , ^Wk +2 = ^Wk -2 ^{- 2(2 +} r i ^{+ 4 r} 2 ) ^Wk -1 ⁺

^{+ (2} + r i + ^{4 r}2 )( r i + ²⁾ — , где r ₂ = aP ₂ n ² / n ² .

Таким образом, равенства (23) и (26) определяют все четыре законтурные неизвестные, выраженные через значения узловых функций на краях и внутри пластины. Исключим законтурные неизвестные из разностных соотношений (18), (19) и (20). Подставляя в эти соотношения равенства (23) и (26), будем иметь

и

A i = r i ^W i , A k = r i ^Wk                ⁽²⁷⁾

в , = g— - 2 fw ₂ + 2 W 3 ,

B ₂ = vw , + 5 w ₂ - 4 w ₃ + w ₄,

B k -i = ^Wk -3 ^{- 4 W}k -2 ^{+ 5 W}k -i ^{+ VW}k ,

^Bk = ^{2 W}k -2 ^{- 2} f ^Wk -i ⁺ g ^Wk ,

где g = 6 – 4 u + uf ; f = 2 + r ₁ + 4 r ₂; u = r ₁ + 2; v = r ₂ – 2. Отметим, что A _i ( i = 2, …, k – 1) и B _i ( i = 3, …, k – 2) по-прежнему определяются равенствами (14).

Итак, однородная система линейных алгебраических уравнений

22 ^{n 4}

an w i - 2 p n A i + — BBj -n t i w i = 0

an

( i = 1, 2, …, k ),                      (29)

аппроксимирующая дифференциальное уравнение (8), содержит теперь только k неизвестных w ₁, w ₂,..., w _k .

Учитывая равенства (14), (27) и (28), перепишем систему (29) в виде матричного уравнения

( D -n T ) W = 0,               (30)

где

D = an ² E - 2 p n ² A + - n y B ;         (3i)

an

T = ^

t 1 0

t ₂

0 '

W =

- q

^W 2

t k J

w _k

Здесь

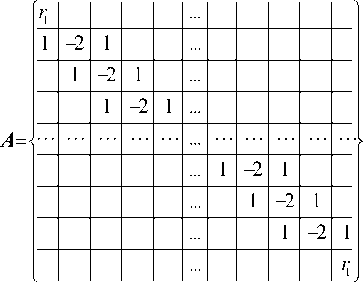
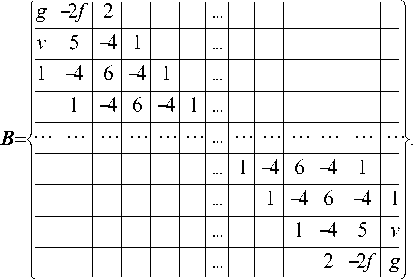
Неуказанные элементы в матрицах А и В равны нулю; в равенстве (31) Е – единичная матрица.

Таким образом, рассматриваемая нами задача устойчивости ортотропной пластины сведена к обобщенной задаче на собственные значения (30). Минимальное собственное значение однородной системы линейных алгебраических уравнений определяет величину критического безразмерного коэффициента устойчивости n . Точность вычислений n оценивается сравнением результатов, полученных при различных числах k. При известном n критическое значение сжимающего усилия N можно получить из уравнения (17):

N cr =П сг j-DD .           (32)

Величина коэффициента n _cr зависит от параметров a , Р , , Р ₂, которые содержат всю информацию о размерах пластины и ее изгибных жесткостях.

Примеры. Рассмотрим примеры определения критического коэффициента устойчивости для некоторых пластин, нагруженных моментом в своей плоскости.

В качестве первого примера решим рассматриваемую нами задачу для изотропной пластины. Изгибные жесткости в этом случае определяются следующими выражениями:

_h 33

D ii = D 22 = E^ D i2 =Ц Еh 2,

D = А -И EhL ,             (33)

³³      2    12

где h - толщина пластины; E = E /(i - ц ² ), здесь Е - модуль упругости, ц - коэффициент Пуассона.

Из формул (i6), (22) и (25) будем иметь a = i/ c ² , здесь c = a / b - отношение сторон пластины; р = i; Р , = ц ; Р ₂ = (i - ц )/2. Таким образом, величина критического коэффициента устойчивости для изотропной пластины зависит фактически от одного параметра с.

Выполним анализ влияния с на величину n для ц = 3. При расчетах число шагов разбиения n принималось равным 50 . Параметр с изменялся в пределах от 1 до 5. Результаты расчетов приведены в табл. 1.

Таблица 1

Зависимость n _cr( c )

c	1	2	3	4	5
n cr	25,71	11,25	7,27	5,39	4,29

Коэффициент устойчивости n cr может быть также представлен в виде аналитической формулы, которая получена обработкой результатов вычислений методом наименьших квадратов:

E 2 = 9,13 ГПа, G ₁₂ = 5,49 ГПа, E ₁ = 142,8 ГПа, р ₁₂ = 2, р ₂₁ = 32.

Результаты расчетов представлены в табл. 2.

Таблица 2

18,9695

H er z                          9 "

( c - 0,272 6 ) 0,

Формула (34) дает вполне приемлемые результаты при определении критического коэффициента устойчивости для изотропной пластины.

Во втором примере рассмотрим пластину, которая образована из однонаправленных или ортогонально ар-

Зависимость параметров с , ϕ , η_cr

c	1,0	2,0	3,0	4,0	5,0
ф	14,0	22,0	22,0	22,0	22,0
П ег	16,17	6,29	3,94	2,88	2,27

мированных тонких слоев, уложенных так, что оси основного армирования составляют с осью x углы ± ф . При боль-

шом числе слоев и одинаковом количестве чередующихся слоев с углами ± ф структуру пластины можно считать однородной и ортотропной. Тогда изгибные жесткости

пластины определяются равенствами _h 3                _h 3               _h 3

D 11 ⁼ A " 12 ’ ^{D 22 = A} 22 12 ’ ^D 12 ^{= A} 12 12 ’

D 33 = A 33^                (35)

где

A 11 = ^E 1 c ф + ^E 2 ⁵ ф + ^{2 E} 12 c Ф ⁵ Ф ;

A 12 = ^E 1 M-12 + ^{( E} 1 + ^E 2 ^{- 2 E} 12 ) c ф ⁵ ф ;

A 2 2 = ^E 1 ⁵ ф + ^E 2 c ф + ^{2 E} 12 c ф ⁵ ф ;

A 33 = ( E 1 + E 2 - 2 E 1 Ц 12 ) c ф² 5 ф² + G 12 (c ф² - 5 ф² ) ² ; (36)

E ₁₂ = E ^₁₂ + 2 G ₁₂; E , =

E 1              ^E 2

1               ; E 2 1                ;

^{1 -} Ц 12 ^ 21           ¹   ^ 12 ^ 21

c ф = cos ф ; 5 ф = sin ф .

Здесь E ₁, E ₂ – модули упругости в направлении армирования и направлении перпендикулярном ему, G ₁₂ – модуль сдвига, р ₁₂, р ₂₁ - коэффициенты Пуассона.

Учитывая равенства (35), из формул (16), (22) и (25) получим

a = ± Щ, ₽ = A ¹^³ ! , ^{c    A} 22           ^A 11 ^A 22

Р ' = п^т- ₽ 2 =

^A 11 ^A 22             ^A 11 ^A 22

Таким образом, для ортотропной пластины коэффициент устойчивости зависит от двух параметров: отношения сторон с и угла армирования ф . Для удобства параметрического анализа преобразуем формулу

П ег

^N cr ^{b 2}

к следующему виду:

ч.

N cr b ²

cr

,

где П ег

D = Eh- . 11₁₂

D 1

= H crV f_x 1 f >2 , здесь f_x 1 = A n/ E 1 , f ,2 = A 22 / E ₁;

Выполним анализ влияния с и ф на величину n cr . Расчеты проводились для углепластика с E ₁ = 142,8 ГПа,

Данные табл. 2 показывают, что максимальный коэффициент устойчивости для квадратной пластины ( с = 1) реализуется при ф = 14 ° . С увеличением удлинения пластины оптимальный угол армирования стремится к 22 ° .

Таким образом, авторами решена задача устойчивости ортотропной пластины, два противоположных края которой свободны, а два других шарнирно закреплены. Пластина нагружена в своей плоскости погонными усилиями, распределенными по линейному закону. Задача определения критического усилия для ортотропной пластины была сведена к вычислению безразмерного коэффициента устойчивости. Величина этого коэффициента зависит от геометрических и упругих параметров пластины. Для решения был использован метод конечных разностей. Критический коэффициент устойчивости определялся как минимальное собственное значение соответствующей системы однородных алгебраических уравнений, аппроксимирующих краевую задачу. Были решены задачи устойчивости для изотропной пластины и ортотропной пластины, состоящей из одинаковых симметрично армированных слоев. В результате выполненного параметрического анализа были определены оптимальные углы армирования для пластин с различными удлинениями. Было исследовано влияние отношения сторон пластины и угла армирования на характер волнообразования при выпучивании.