Устойчивость пологих ортотропных оболочек двоякой кривизны при шарнирно-подвижном закреплении контура

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2018PNRPU MECHANICS BULLETIN

Оболочечные конструкции широко используются в разных областях техники, и их исследование важно для многих прикладных задач: например, подобные конструкции применяются в строительстве и машиностроении [1, 2]. Оболочечные конструкции подвергаются воздействию различных нагрузок [2–14]. Так, в работах [3–6] рассматривается влияние температуры. В работах [7, 8] проводится анализ устойчивости конструкций под воздействием осевого сжатия, причем в работе [7] также проводятся расчеты устойчивости под воздействием точечной нагрузки. В [2, 9–11] рассматривается воздействие статической поперечной равномерно-распределенной нагрузки. В работах [12–14] исследуется процесс деформирования конструкций, находящихся под воздействием динамической нагрузки, причем в [13] также исследуется состояние конструкции под воздействием осевого сжатия.

Конструкции разной геометрии деформируются по-разному, поэтому тип рассматриваемых конструкций также имеет большое значение для исследования их напряженно-деформированного состояния. В большинстве рассмотренных работ [3, 4, 7, 12, 16] исследуются цилиндрические оболочки, в [13, 14] – конические, в [16] исследуются тороидальные, в [2, 17, 19] – пологие двоякой кривизны, в [20] – прямоугольные пластины. В работе [10] приводится общая модель деформирова- ния для оболочек канонической формы (тороидальные, цилиндрические, конические, пологие двоякой кривизны). Исследование устойчивости таких конструкций является актуальной задачей.

Также актуален вопрос облегчения подобных конструкций, для чего применяются современные композиционные материалы, такие как стеклопластики, боро-пластики, органопластики, углепластики и текстолиты, а также полимеры [17, 18, 21, 22]. Их использование позволяет существенно снизить вес конструкции.

Приведенные материалы обладают свойством ортотропии, т.е. его физические свойства различны по взаимно перпендикулярным направлениям. Благодаря этому они превосходят традиционные материалы и сплавы по своим механическим и физическим свойствам. Так, композиционные материалы обладают большой удельной прочностью [19] и стойкостью к воздействиям высоких температур и вибрационным нагрузкам [17].

Применение материалов более сложной структуры приводит к необходимости решения задач уточнения и усовершенствования математической модели их деформирования и выбору устойчивого и точного алгоритма ее исследования [23].

Для исследования оболочечных конструкций применяются различные модели. Так, могут быть использованы математические модели в форме функционала полной потенциальной энергии деформации [2, 23]. Также, что особенно удобно в случае шарнирно- подвижно опертых по контуру конструкций, используются уравнения в смешанной форме [10, 12, 24–28]. Для решения задач устойчивости могут использоваться различные численные методы, такие как метод конечных элементов [2, 20, 29] и метод Ритца [23], а также метод Бубнова–Галеркина [12–15].

Для исключения концентрации напряжений вблизи контура, особенно в угловых точках оболочки, используется шарнирно-подвижное закрепление контура конструкции [30]. Подобное закрепление уменьшает вероятность потери прочности конструкции, что особенно важно, если она изготовлена из ортотропного материала1.

1. Математическая модель деформирования пологой оболочки

(MF (Ф) + k,F2 (Ф)) - £ (F ( Ф) 01 + F3 (Ф)02) -

~( F 2 ( Ф ) 0 2 + F 3 ( Ф ) 0 1 ) + Q + ^ + q = 0; д у                     d x    д у

d dx

—

d

+ 8y

—F ( Ф )-- ^2- f ( ф ) 1 E^h ^2V ’ E_xh ^1V J

Eh^{F (Ф)-}

+

^ f ( ф ) I = E 2 h  ²     JJ

Будем рассматривать пологие оболочки двоякой кривизны, квадратные в плане. Срединную поверхность оболочки толщиной h примем за координатную. Оси x , y ортогональной системы координат направлены по

= -(x22 -X1X2 + kxX2 + kyX);

df    E1 h3    л .   . и 4h\. I л                  A (X1 +^21X2) +Г I 10^12 X12 I  Qx = 0;

dx (12(1 - Ц12Ц21)             J  dу (12

d f    E2h3     /   ,      aY d Г h3

2(X?+^i?Xi) +G7X17  - Qv = 0, dy (12 (1 -Ц12Ц21)(          1 )J  dx (12  12Л12 J

линиям главных кривизн оболочки. Ось z ортогональна срединной поверхности и направлена в сторону вогну-

тости.

где E , E ₂, Pj₂, ц₂₁ - модули упругости и коэффициенты

Пуассона материала; G , G , G – модули сдвига в

Параметры Ляме и параметры кривизны пологой оболочки двоякой кривизны соответственно равны плоскостях xOy, x Оz, у Оz соответственно; Ох = dW dx ’

A = 1, B = 1, к = —, к xRyR

SW

O2 =-^^ [10]; d у

W ( x , у ) - перемещение точки средин

Оболочка по контуру закреплена шарнирноподвижно, находится под действием равномерно-распределенной поперечной нагрузки q (рис. 1).

ной поверхности оболочки вдоль оси z ; Xv Х2 — функции изменения кривизн, Хх2 — функция изменения кру- чения,

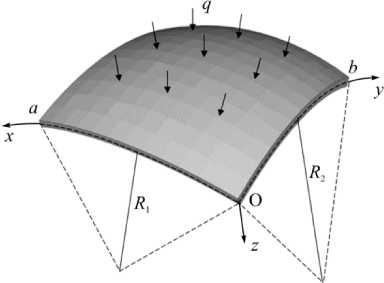
Рис. 1. Схематичное изображение пологой оболочки Fig. 1. Schematic representation of a shallow shell

d^_x       д^ у        1 fdT_x  d^ у I

Х 1 =       ; Х 2 = д ; Х 12 = ~I _д⁺       I .    ⁽²⁾

д x         д у         2 ^ д у    д x J

Здесь функции Т , Т - углы поворота отрезка нормали к срединной поверхности в сечениях x O z , у О z соответственно;

Q_x = khG 13 ( Т x -0 , ) ; Q_y = khG 23 ( Т у -0 ₂ ) , к = 5.

В соотношениях (1) F ( Ф ) , F ₂ ( Ф ) , F ₃ ( Ф ) - обозначения усилий через функцию напряжений в срединной поверхности оболочки Ф ( x , у ) :

В качестве математической модели деформирования оболочечной конструкции воспользуемся уравнениями в смешанной форме, полученными в работе [10] для оболочек общего вида (пологих двоякой кривизны, цилиндрических, конических, тороидальных и др.), а также позволяющими учесть наличие подкрепления ребрами жесткости. После некоторых упрощений для гладких пологих оболочек двоякой кривизны получим

F 1 ( ^Ф ) =

д ² Ф _ "i? ^;

F 2 ( ^Ф ) =-гт; F 3 ( ^ф )     - - . (3)

d x             d x д у

Здесь также используется упрощенная форма функций изменения кривизн и кручения, соответствующая модели Кирхгофа–Лява [10]:

„    SO,    . d0₂    .      1 <50,   d0₂I

^X1 = "15 ;    ^X2 = "H ;    ^X12 = I ""5"   ⁺ ""5 I ^.

d x        d x        2 усу   d x J

Описанные выше уравнения представляют собой систему уравнений равновесия в смешанной форме для оболочек из ортотропного материала с учетом геометрической нелинейности и поперечных сдвигов. Неизвестными функциями здесь являются W(x,у), Ф(x,у), — x (x, у ), —у (x, у ) .

2. Алгоритм решения уравнений математической модели

Для решения полученных уравнений относительно неизвестных функций     W ( x , у ) , Ф ( x , у ) , V Д x , у ) ,

— ( x , у ) применим метод Бубнова-Галеркина. Тогда неизвестные функции будут иметь вид

N

W (x, у ) = £ W (k) X 1( k) Y 1( к);

к = 1

N

Ф ( x , у ) = £ ^ф ( к ) X 2 ( к ) Y 2 ( к ) ;

к = 1

N

V x ( x , у ) = £ — x ( к ) X 3 ( к ) Y 3 ( к);

к = 1

N

Vу (x,у) = ! —у (к)X4(к)Y4(к).

к = 1

Здесь W ( к ) , Ф ( к ) , — Д к ) , — ( к ) - неизвестные числовые параметры; X 1 ( к ) - X 4 ( к ) , Y 1 ( к ) - Y 4 ( к ) -некоторые аппроксимирующие функции.

Аппроксимирующие функции    X 1 ( к ) - X 4 ( к ) ,

Y 1 ( к ) - Y 4 ( к ) выберем исходя из краевых условий при шарнирно-подвижном закреплении контура оболочки:

при x = 0, x = a

аппроксимирующие функции (8), в систему уравнений в смешанной форме (1). Обозначим первое уравнение L 1 ( W , Ф , V _x , V _у ) , второе - L 2 ( W , Ф , V _x , V _у ) , третье - L 3 ( W , Ф , V x , V у ) , четвертое - L 4 ( W , Ф , V x , V у ) . Затем строим систему F из 4 N уравнений относительно неизвестных числовых параметров W ( к ) , Ф ( к ) , V x ( к ) , V у ( к ) :

Гг ^ал  ,

JJ L 1 ( W , Ф , V x , V у ) X 1 ( к ) Y 1 ( к ) dxdy

L ⁰⁰

ab

N

^- к = 1

N

F =

И L 2 ( W , Ф , V x , V _у ) X 2 ( к ) Y 2 ( к ) dxdy

ab

- к = 1

N

= о

JJ L ( W , Ф , V, , V ) X 3 ( к ) Y 3 ( к ) dxdy

L^{00                      у}                         - ₁ = 1

r abb   у                                           I ^N

J J L ₄ ( W , Ф , V x , V _у ) X 4 ( к ) Y 4 ( к ) dxdy

00                                                 - к = 1 _v

Система (9) нелинейная в силу нелинейности самой рассматриваемой модели. Для ее решения применим метод Ньютона.

В соответствии с методом Ньютона составим матрицу Якоби F' данной системы

—у = 0, -2- = 0, W = 0, —x = 0, Vу = 0; (6) дx       дуд при у = 0, у = b а 2ф     а2Ф-—

= 0,      = 0, W = 0, —у = 0, —,= 0.(7)

д x ²         д у ²                  д у

Тогда в качестве аппроксимирующих можно принять следующие тригонометрические функции:

, _       Г ( 2 к - 1 ) п A       , _       Г ( 2 к - 1 ) п A

X 1(к) = sin  -----— x ;  Y 1(к) = sin  

I a     J              I bJ

, _       Г ( 2 к - 1 ) п A        , _       Г ( 2 к - 1 ) п A

X2(к) = sin  -----— x ;  Y2(к) = sin   ab

"       . J               XJ

, _       Г ( 2 к - 1 ) п A       , _       Г ( 2 к - 1 ) п A

X3(к) = cos  -----— x ; Y3(к) = sin  

I a     J               I bJ

, _       Г ( 2 к - 1 ) п A        , _       Г ( 2 к - 1 ) п A

X4(к) = sin  -----— x ;  Y4(к) = cos   ab

В соответствии с методом Бубнова–Галеркина подставляем разложения искомых функций (5), используя

Г^дF1( k )1 ^{д W} ( I ) к. ^,

Г —> , Ч пА'

^{д W} ( I ) к ^, "-F³ ( к ) 1 N д W ( I ) _t

^F⁴ ( ^к ) 1 N l^{- w} ( I ) - к ,.

rfFk ^ ) 1

1^дФ ( I ) - к , I

№(к ) 1 N

1^-ф < I ) - к ,.

I N

1^-ф ( I ) - к ,.

ГдЕ^^ к ) 1 N [^-Ф ( I ) - к ,.

r^Fka 1

-v x (I) к , г _       -,/V

^{- f2} ( ^к ) l^-V x ( I ) - к ,.

- f ³ ( к ) " N -— x ( i )!,. ~aFW 1 N L-v x ( i ) - к.

'-F¹ ( к )"

-V у ( I )

- F 2( к )~	N	(10)
-—, ( I )
		= 0
- F 3( к )~	N
-—, ( I )	к , I = 1
- F 1 ( к )~ -—, ( I )	N к , 1 = 1 J

Наконец, выбирается начальное приближение { W 0 ( I ) , ^Ф 0 ( I ) , ^V x 0 ( I ) , ^V у 0 ( I ) , I = 1.. N } ^и решается система относительно вектора поправок { A W ( I ) , АФ , ( I ) , AV x 1 ( I ) , AV у 1 ( I ) , I = 1.. N } :

Г          A

	La w ( I ) -
F ' ( W 0 , Ф 0 , — x 0 , — у 0 ) •	L Aф 1 ( I ) -	= - F ( W 0 , Ф 0 , V x 0 , — у 0 )

L ^AV x 1 ( I ) -

I^AV у 1 ⁽ I ) -J

Отсюда находятся значения на следующем шаге:

W 1 ( I ) = W 0 ( I ) + A W 1 ( I ) , ^Ф 1 ( I ) = ^Ф 0 ( I ) ^{+ AФ} 1 ( I ) , V x 1 ( I ) = — x ( I ) + AV x ( I ) , ^V у 1 ( I ) = ^V у ( I ) + ^AV у ( I ) ,

I = 1... N   (12)

Приведенный итерационный процесс продолжается до тех пор, пока не будет выполнено условие

N

J Z ( ^A W ( I ) +АФ k ( I ) +AV xk ( I ) + av yk ( I ) )

^V I =1 ,                                           — <  10 - 3 . (13)

N

J Z ( W k ² ( I ) +ф 2 ( I ) +V xk ( I ) +V yk ( I ) )

v I =1

Для улучшения скорости сходимости метода рекомендуется использовать в качестве начального приближения на очередном шаге значения, полученные на шаге предыдущем.

Полученные коэффициенты W ( k ) , Ф ( k ) , ¥Д k ) , V ( k ) подставляются в разложение (5), таким образом находятся аппроксимации неизвестных функций при заданной нагрузке q .

При исследовании устойчивости оболочек решается геометрически нелинейная задача и строится график зависимости «нагрузка–прогиб» в некоторой точке оболочки, например в ее центре. Анализируются экстремумы этого графика, и таким образом, находятся верхние и нижние критические нагрузки. При этих нагрузках «хлопком» происходит переход на новое равновесное состояние. По сути дела для нахождения критических нагрузок применяется критерий Ляпунова, когда малому изменению входного параметра (нагрузки) соответствует существенное изменение выходного параметра (прогиба).

• 3.    Верификация модели

Прежде чем приступить к исследованию устойчивости оболочечных конструкций, необходимо провести верификацию математической модели для проверки ее адекватности. Сравнение проводится с результатами, полученными в [4] и [7].

В рассмотренных примерах исследовалась цилиндрическая оболочка, выполненная из алюминия, а также шарнирно-подвижно закрепленная по контуру. Цилиндрическую оболочку можно рассматривать как частный случай пологой оболочки двоякой кривизны, но с нулевым коэффициентом кривизны для одной из сторон: k_x = 0 или k y = 0, т.е. один из радиусов равняется бесконечности.

Параметры конструкции геометрические:

h = 0,01 м, a = 0,2м, b = 0,2003м, k_x = 0 м ^{- 1}, k y = 1 м ^{- 1};

физические:

E_v = E₂ = 7 • 10 4 МПа, ц₁₂ = ц₂₁ = 0,3,

G_n = 26923,08 МПа, G ₁₃ = G ₂₃ = 76923,08 МПа.

Исследование устойчивости приведенной конструкции проводилось в среде аналитических вычислений Maple с удержанием N = 16 членов разложения в методе Бубнова–Галеркина (5). На рис. 2 приводятся графики зависимости «нагрузка–безразмерный прогиб в центре» для данной цилиндрической панели, полученные в [4] и [7], а также по предложенной в данной работе методике.

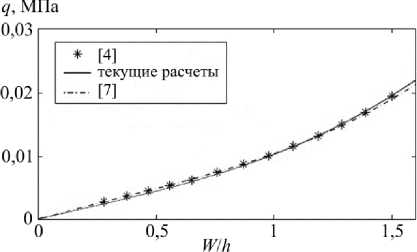
Рис. 2. Сравнительный анализ расчета конструкции

Fig. 2. Comparative analysis of the structure calculation

Как видно из представленного графика, все три кривые достаточно близко лежат друг к другу. Таким образом, можно сделать вывод об адекватности разработанной модели и применимости к ней приведенного алгоритма.

• 4.    Расчетные параметры

Рассматривались конструкции трех разных размеров (табл. 1) из четырех разных материалов (табл. 2). Таким образом, всего было исследовано 12 конструкций (табл. 3)

Таблица 1

Варианты геометрических характеристик

Variants of geometric characteristics

Table 1

Характеристика	Вариант геометрии
	1	2	3
h , м	0,09	0,09	0,09
а = b , м	5,4	10,8	18
R 1 = R 2, м	20,25	40,05	45,27

Таблица 2

Варианты физических характеристик материала

Table 2

Variants of the physical characteristics of the material

Характеристика	Углепластик M60J/Epoxy [8]	Графит AS/3501/Epoxy [7]	E-Glass/Epoxy [7]	Стеклопластик Т10/UPE22-27/ Epoxy [8]
Е 1 , МПа	330000	138000	60700	29400
Е 2 , МПа	59000	8960	24800	17800
G 12 = G 13 = G 23 , МПа	3900	7100	12000	3010
µ 12	0,320	0,300	0,230	0,123
µ 21	0,057	0,019	0,094	0,074
Показатель анизотропии	5,59	15,4	2,44	1,65

Таблица 3

Варианты рассматриваемых конструкций

Table 3

Variants of the constructions under consideration

Вариант конструкции	Материал	Вариант геометрических характеристик
1	Углепластик M60J/Epoxy	1
2	Графит AS/3501/Epoxy	1
3	E-Glass/Epoxy	1
4	Стеклопластик Т10/UPE22-27/Epoxy	1
5	Углепластик M60J/Epoxy	2
6	Графит AS/3501/Epoxy	2
7	E-Glass/Epoxy	2
8	Стеклопластик Т10/UPE22-27/Epoxy	2
9	Углепластик M60J/Epoxy	3
10	Графит AS/3501/Epoxy	3
11	E-Glass/Epoxy	3
12	Стеклопластик Т10/UPE22-27/Epoxy	3

Для определения оптимального числа членов разложения проведем сравнение получаемых данных при N = 4,9,16,25. Будем рассматривать конструкции 9, 10, 11 и 12, т.е. вариант геометрических характеристик 3, выполненный из всех четырех приведенных материалов. Результаты для варианта конструкции 9 приведены на рис. 3, для варианта 10 – на рис. 4, для варианта 11 – на рис. 5, для варианта 12 – на рис. 6.

Обозначение W ⁱ соответствует прогибу в центре конструкции при i = N членах разложения, а W^ -наибольшему прогибу оболочки.

Для оболочки варианта 10 также проведем сравнение значений нормальных напряжений с , с и интенсивности напряжений с . Анализ значений будем проводить в центре конструкции, так как на краях (в том числе в угловых точках) значения всех компонентов напряжений будут равны нулю. Полученные результаты приведены на рис. 7–9 и в табл. 4.

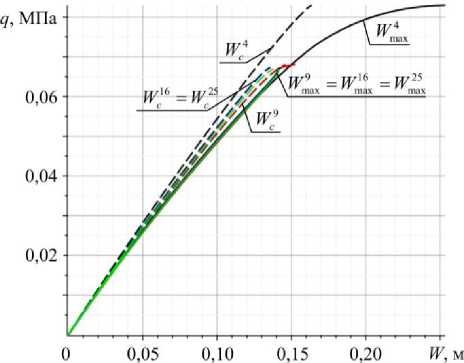
Рис. 4. Сходимость результатов для варианта конструкции 10

Fig. 4. Convergence of results for the 10th variant of the construction

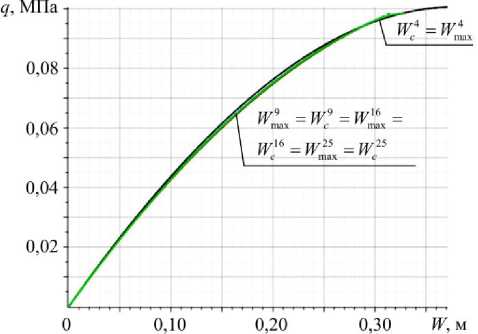
Рис. 3. Сходимость результатов для варианта конструкции 9

Fig. 3. Convergence of results for the 9th variant of the construction

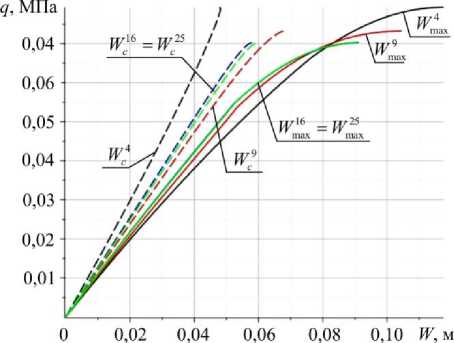
Рис. 5. Сходимость результатов для варианта конструкции 11

Fig. 5. Convergence of results for the 11th variant of the construction

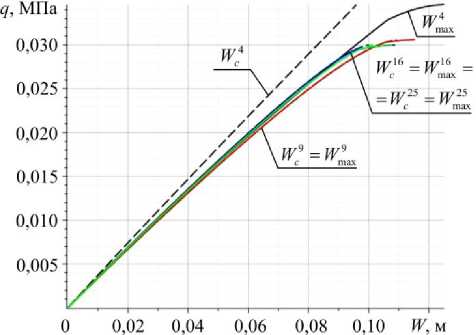
Рис. 6. Сходимость результатов для варианта конструкции 12

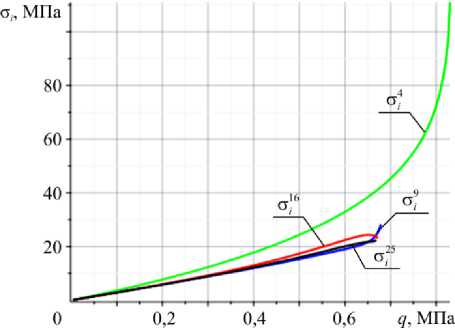
Рис. 9. Сходимость интенсивности напряжений с, для варианта конструкции 10

Fig. 9. Convergence of the intensity strain с for the 10^th variant of the construction

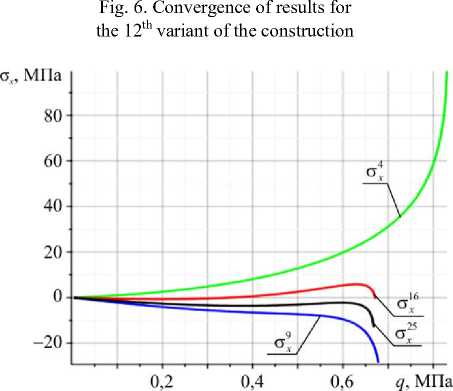
Рис. 7. Сходимость напряжений с для варианта конструкции 10

Fig. 7. Convergence of а_х strains for the 10^th variant of the construction

Таблица 4

Значения напряжений в центре оболочки варианта 10 в момент потери устойчивости

Table 4

The strain values corresponding to the critical buckling load in the center of the 10th variant of the construction

N	σ х , МПа	σ у , МПа	σ i , МПа
4	99,38	–20,38	110,98
9	–28,55	–27,98	28,27
16	–0,48	–23,32	23,08
25	–13,01	–26,03	22,55

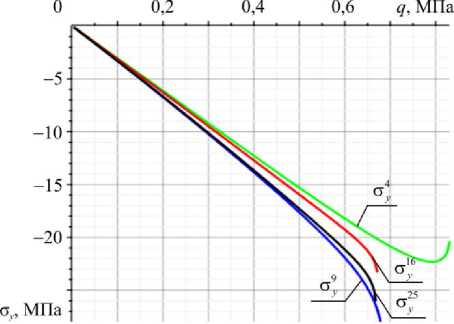
Рис. 8. Сходимость напряжений с y для варианта конструкции 10

Fig. 8. Convergence of с strains for the 10^th variant of the construction

Полученные значения напряжений для оболочки варианта 10 показывают хорошую сходимость для σ у и σ _i , для σ _х сходимость есть, но выражена слабее.

Как можно заметить из представленных в данном разделе графиков и таблиц, расчеты на устойчивость при N = 16 и N = 25 дают близкий результат вне зависимости от материала, из которого изготовлена конструкция. Таким образом, все дальнейшие расчеты будут проводиться при удержании N = 16 членах разложения в методе Бубнова–Галеркина (5).

• 5.    Исследование устойчивости

Проводится расчет устойчивости 12 конструкций, приведенных в табл. 3, с геометрическими характеристиками, указанными в табл. 1, и физическими характеристиками, указанными в табл. 2.

На рис. 10 приведены графики «нагрузка–прогиб» для варианта геометрических параметров 1 для всех четырех материалов. Индекс W ^k соответствует наибольшему прогибу конструкции из материала k , а индекс W ^k – прогибу в центре. Для рассматриваемой конструкции наибольший прогиб равен прогибу в центре оболочки: W ^ax = W* .

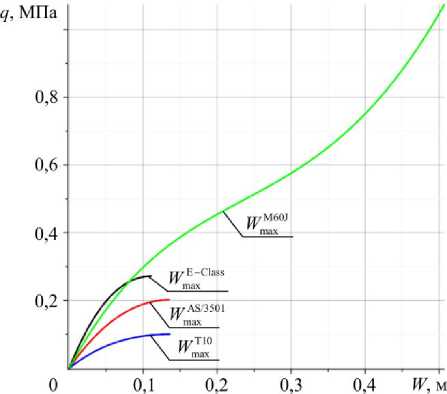
Рис. 10. График зависимости «нагрузка-прогиб» для варианта геометрических параметров 1

Fig. 10. Graph of the "load-deflection" dependence for the 1st variant of geometric parameters

На рис. 11 приведены графики «нагрузка-прогиб» для варианта геометрических параметров 2 для всех четырех материалов.

На рис. 12 приведены графики «нагрузка-прогиб» для варианта геометрических параметров 3 для всех четырех материалов.

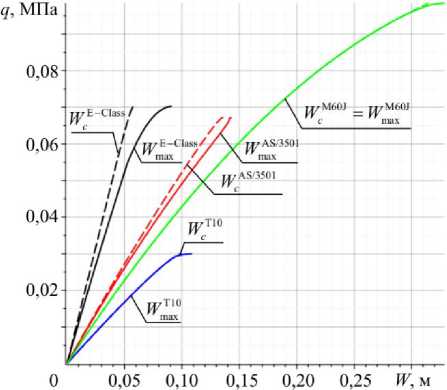
Рис. 12. График зависимости «нагрузка-прогиб» для варианта геометрических параметров 3

Fig. 12. Graph of the "load-deflection" dependence for the 3rd variant of geometric parameters

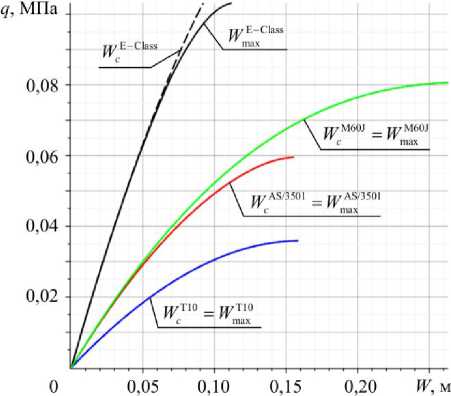
Рис. 11. График зависимости «нагрузка-прогиб» для варианта геометрических параметров 2

Fig. 11. Graph of the "load-deflection" dependence for the 2nd variant of geometric parameters

Анализируя полученные результаты, можно заметить, что для конструкций с вариантом геометрических параметров 1 прогиб в центре совпадает с максимальным для всех четырех материалов. Это связано с отношением длины сторон оболочки к ее толщине. Для остальных двух вариантов геометрических параметров при той же толщине размеры в плане существенно больше, чем у первого варианта. Отсюда возникает различие между значениями прогиба в центре конструкции и ее максимальным прогибом, особенно вблизи критической нагрузки потери устойчивости. Для вариантов конструкций 5–8 (вариант геометрических параметров 2) это характерно только для стекловолокна E-Glass/Epoxy, а для вариантов конструкций 9–12 (вариант геометрических параметров 3) – уже для всех исследуемых материалов.

Все значения критических нагрузок q , при которых оболочки теряют устойчивость, сведены в табл. 5, а значение наибольшего прогиба, соответствующего этой нагрузке, – в табл. 6.

Таблица 5

Значения критических нагрузок потери устойчивости q_kr

Table 5

The values of the critical loads of buckling q_kr

Вариант геометрии	q kr , Мпа
	Углепластик M60J/Epoxy	Графит AS/3501/Epoxy	E-Glass/Epoxy	Стеклопластик Т10/UPE22-27/ Epoxy
1	0,575	0,205	0,265	0,105
2	0,081	0,059	0,120	0,036
3	0,098	0,067	0,070	0,030

Таблица 6

Значения наибольшего прогиба W ^kr , соответствующего потере устойчивости

The values of the maximum deflection W ^kr corresponding to the critical buckling load

Table 6

Вариант геометрии	kr max , м
	Углепластик M60J/Epoxy	Графит AS/3501/Epoxy	E-Glass/Epoxy	Стеклопластик Т10/UPE22-27/ Epoxy
1	0,300	0,130	0,115	0,135
2	0,261	0,155	0,115	0,159
3	0,328	0,143	0,091	0,109

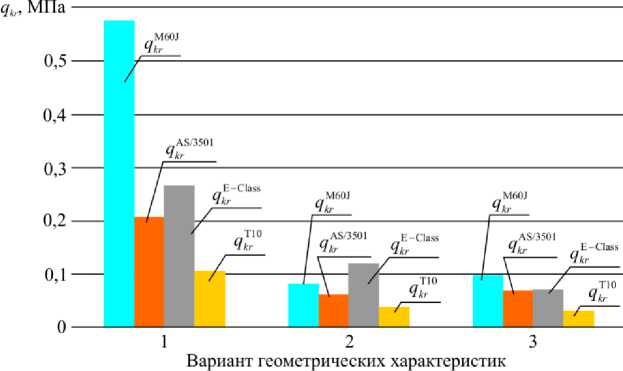
Рис. 13. Критические нагрузки потери устойчивости в зависимости от выбранного материала

Fig. 13. The critical buckling loads, depending on a chosen material

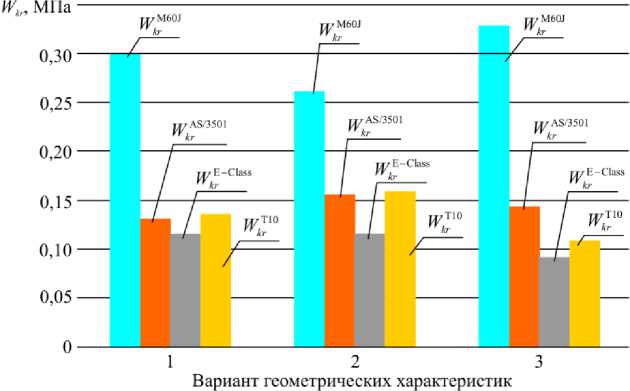
Рис. 14. Значения максимального прогиба, соответствующего потере устойчивости, в зависимости от выбранного материала

Fig. 14. The values of the maximum deflection corresponding to the critical buckling load, depending on a selected material

Для лучшего восприятия данных в табл. 5, 6 те же самые значения приведены на рис. 13 и 14 соответственно. На следующих графиках индекс W ⁱ обозначает максимальный прогиб оболочки из материала i , соответствующий потере устойчивости, то есть при нагрузке q = q ⁱ .

Как видно из представленных графиков и таблиц, наибольшее значение критической нагрузки потери устойчиво- сти из рассмотренных материалов дают углепластик M60J/Epoxy и стекловолокно E-Glass/Epoxy. При этом оболочки, выполненные из стекловолокна E-Glass/Epoxy, к моменту достижения критической нагрузки потери устойчивости имеют наименьший максимальный прогиб среди всех четырех рассматриваемых материалов, в то время как конструкции из углепластика – наибольший.

Таким образом, можно говорить о том, что наилучшим выбором среди четырех рассмотренных материалов будет E-Glass/Epoxy в силу высокой устойчивости и большой несущей способности выполненных из него конструкций. Однако заметим, что углепластик M60J/Epoxy в данном случае был выбран однонаправленный, в то время как стеклопластик имеет волокна, уложенные в обоих направлениях. Укладка волокон углепластика в обоих направлениях может сделать его наиболее оптимальным материалом.

Заключение

В ходе исследования рассматривались пологие оболочки двоякой кривизны, прямоугольные в плане. Оболочки закреплены по контуру шарнирно-подвижно и выполнены из ортотропного материала. По результатам исследования были получены следующие выводы и результаты: