Устойчивость процесса алмазного выглаживания

Введение. Методы обработки деталей поверхностным пластическим деформированием достаточно распространены. Они позволяют управлять шероховатостью поверхности, остаточными напряжениями, микротвёрдостью, а также их распределением в приповерхностном слое и др. В результате изменяется износостойкость деталей, контактная выносливость, коррозионная стойкость [1‒5]. Выглаживание, как один из методов отделочно-упрочняющей обработки, осуществляется специальным инструментом-выглаживателем, который скользит под определённым давлением по обрабатываемой поверхности, пластически деформируя её, сглаживая при этом микронеровности (следы от предыдущей обработки) и уплотняя поверхностный слой. Поверхности, обработанные алмазным выглаживанием, обладают высокой износостойкостью при образовании пар трения и высокой усталостной прочностью. Однако все эти факторы имеют место в том случае, когда траектории движения инструмента относительно заготовки являются устойчивыми. В противном случае рассматриваемый процесс, как правило, сопровождается автоколебаниями, параметры которых ухудшают качество формируемой поверхности. В статье ставится задача определить факторы, влияющие на устойчивость процесса выглаживания. При этом рассматривается устойчивость траекторий движения вершины наконечника алмазного выглаживателя относительно образца.

Математическое моделирование динамики процесса. Схема процесса приведена на рис. 1. Технологический процесс формируется в результате взаимодействия подсистем инструмента и обрабатываемой детали через динамическую связь, которая образуется в области контакта алмазного наконечника и детали. Эта схема соответствует процессу трения индентора с образцом, который достаточно подробно рассмотрен в работах [6‒11]. Конструктивные особенности инструмента таковы, что между наконечником и корпусом устанавливаются пространственные упругие элементы. Поэтому при изучении динамики деформациями заготовки можно пренебречь. Если заданы внешние силы F (t) = {F1 (t), F2 (t)}T , то уравнение упругих деформаций можно представить в виде mdtX+^dx+cx=f (t),                            (1)

Работа выполнена по теме № 7.5477.2011 в рамках выполнения госзадания Минобрнауки России в части НИР.

где X ( t ) = { X ( t ) . X 2 ( t ) }^T

—

вектор упругих деформационных смещений; m =

m 0 0 m ,

h =

^h 1,1 h 1,2

h 2,1 h 2, 2

, c =

c 1,1

c 1,2

c 2,1 c 2, 2

— соответственно матрицы инерционных, скоростных и упру-

гих коэффициентов, которые являются симметричными и положительно определёнными.

Предварительные исследования также показали, что на основе оператора поворота координат имеется возможность в системе выделить углы ориентации коллинеарных направлений, причем для матрицы упругости и скоростных коэффициентов они совпадают. Угол ориентации коллинеарных осей с учетом высказанных выше особенностей равен (рис. 1, а )

a = 2arctg

C.1 ) J .

—

l ( c 2.2

(            ^

^Z c 1,2

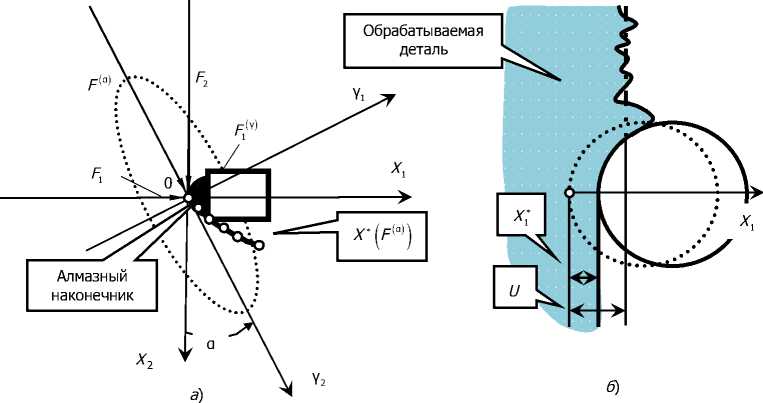
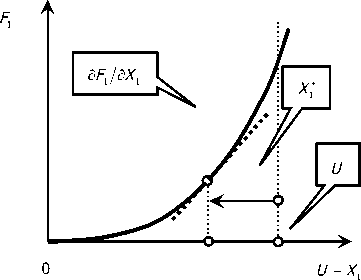
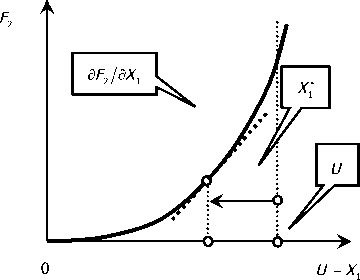
Рис. 1. Система динамической модели: а — координаты, в которых отсчитывается упругое деформационное смещение вершины инструмента и внешние силы; б — схема формирования поверхности выглаживания; в — F ₁ и F ₂ , функции сближения алмазного наконечника с обрабатываемой поверхностью

в )

Таким образом, если оси X = {X1, X2}T и y = {Y1, Y2}T совпадают (a = 0), то матрицы c и h также становятся диагональными, а система (1) распадается на два скалярных уравнения. Для раскрытия особенностей динамики процесса выглаживания необходимо силы F (t) = {F1 (t), F2 (t)}T представить в координатах состояния X (t) = {Х1 (t), X2 (t)}T . При этом необходимо учесть две главных особенности зависимости сил от координат состояния: они увеличиваются при возрастании внедрения алмазного наконечника в обрабатываемую поверхность (рис. 1, б и в) [7, 8]; имеет место запаздывание изменения сил по отношению к вариациям внедрения « U - Х1», зависящее от точки равновесия X*. Причём, запаздывание определяется объёмом пластической деформации материала, приходящимся на единицу пути инструмента. Это путь, потраченный на пластическую деформацию. Поэтому запаздывание зависит от скорости резания. Кроме этого, в процессе внедрения имеет место перераспределение составляющих сил резания [12‒14]. Поэтому величины запаздывания по отношению к силам F1 и F2 различны.

Зависимость установившихся значений сил от внедрения (рис. 1, в) в дальнейшем будем называть функциями сближения. С учётом отмеченных выше особенностей, уравнения динамики процесса выглаживания в развернутом виде можно представить в виде следующей системы m d X1 + h i dt + h i dX2 + C Xi + C X2 = F (U - Y) + ft); dt2       1, 1 dt 2, 1 dt 1, 1 1     2, 1 2     1          1      1

<

d2X     dX m —1 + h , —1- + h dt2      1'2 dt 2-2

dY.

T Y^+Y = X i ;

dt ² + C i,2 X i + C ₂ , ₂ X 2 = F 2 ( U - Y 2 ) + f 2 ( t ) ;

T dY + y = X T2 dt 2     1, где T1, T2 — аргументы, моделирующие запаздывания сил в виде апериодических звеньев; f1 (t), f2 (t) — силовой шум процесса, определяющий возмущённое движение системы относительно своего стационарного состояния. Будем анализировать стационарное состояние системы, ко-d2X dX  d2X  dX dY dY торое характеризуется: -t^- = -t^ = -dt = dt = t = -dt- = 0, U = const, fi(t) = f2(t) = 0 .

Тогда координаты точки равновесия определяются из системы

C 1,1 X ; + c 2,1 X 2= F i ( U - x ;) ;

C1,2 x;+ c 2,2 X2= F2 (U - x;) , где Xi, X2* — координаты точки равновесия. Для анализа устойчивости необходимо рассматри- вать возмущенное линеаризованное уравнение в вариациях относительно точки равновесия

X 1 , X

*

d2x    dx m —т + h — + cx = 0, dt2     Σ dt Σ ,

с 1,1

где c _z =

₊д Ф 1 8 x 1

c 1,2

, ^д Ф 2

8 x 1

c 2,1

c 2, 2

с 1, 1, Σ c 2,1 c 1, 2, Σ c 2,2

h z =

^h 1,1

h 1,2

—

—

т д Ф 1

T ₁

d x 1

Т д Ф 2

T ₂

5 x 1

h 2,1

h 2, 2

h 1, 1, Σ h 2,1 h 1, 2, Σ h 2,2

суммарная

матрица жёсткости, учитывающая реакцию со стороны процесса выглаживания и суммарная матрица скоростных коэффициентов; x = {x1 (t), x2 (t)}T — вектор вариаций упругих деформационных смещений относительно точки равновесия Х1*, X2*; (X (t ) = X*+ x (t)), ф. | x, T dx1, ф21 x, T dx ф1I 1, 1 dt J, ф2I 1, 2 dt

— нелинейные функции, рассматриваемые в вариациях отно-

сительно точки равновесия. Они обладают свойствами:

< 0,        <  0, ф ( 0,0 ) = 0,

9x1         9x1           1 v /

ф ( 0,0 ) = 0. В матрицах h и c приняты во внимание знаки при производных ^{д ф} 1 и ^{д ф} 2 .

^{2                                   22}                                                                   9 x .       9 x .

Для конкретизации системы (3) были выполнены исследования, направленные на параметрическую идентификацию и изучение свойств функций сближения F 1 ( U - X . ) и F 2 ( U - X . ) . Во всех случаях при изучении функций сближения рассматривались алмазные инструменты, наконечники которых имели сферическую форму. При этом принято во внимание, что ( U - X . ) = t_p . Здесь t_p — текущее значение глубины обработки с учётом упругих деформационных смещений. Не останавливаясь на деталях, отметим, что во всех случаях функции сближения можно аппроксимировать параболой, т. е.

F .-V a ( t , ) 2 при: t p >  0,

0 при: t p <  0;

Г 2                                                              ⁽⁶⁾

F = a 2 ( t P ) при: t P >  ⁰,

² ^ 0       при: t_p<  0.

где a ₁ , a ₂ — параметры, имеющие смысл давления обрабатываемого материала на единицу пло-

щади контакта в [ кг/мм² 1 . Тогда ^{д ф1}

L J          9x1

и

дф,

—² в (5) для точки равновесия X. соответственно

9 x 1                                         ¹

равны

X -2а- (U - X;);

I x r = 2 a 2 ( ^{U - X} -> •

Смещение инструмента по направлению X ₂ * не вызывает вариаций сил, так как в этом случае нет изменений площади контакта инструмента и обрабатываемой части заготовки. Случай отрыва инструмента от поверхности обрабатываемой детали не рассматривается.

Установлено, что существует два механизма потери устойчивости траектории. Первый обусловлен формированием циркуляционных сил контактного взаимодействия, возникающих в результате того, что суммарная матрица упругости является несимметричной. Второй обусловлен преобразованием симметричной составляющей матрицы скоростных коэффициентов из положительно определённой в отрицательно определённую. Это происходит за счёт запаздывающих аргументов в уравнении (5). При этом принимается во внимание известное из механики положение, что кососимметричные составляющие матриц скоростных коэффициентов, формирующие гироскопические силы, не могут стабилизировать равновесие системы, если оно неустойчиво. Во всех

случаях увеличение предварительного натяга положения вершины инструмента относительно поверхности заготовки вызывает возрастание циркуляционных сил и способствует преобразованию положительно определённой матрицы скоростных коэффициентов из положительно определённой в отрицательно определённую. Для анализа же устойчивости системы необходимо рассматривать следующее характеристическое уравнение

Д ( p ) =

mP ² + [ h i, 1 - 2 T i a i ( U - X 1 ) ] p + [ c , 1 + 2a_x ( U - X () ] [ h i, 2 - 2 T 2 a 2 ( U - X () ] p + [ C 1,2 + 2 a, ( U - X () ]

^h 2,1 P ⁺ c 1,2

mP ² + h 2,2 P ⁺ c 2,2

= 0

Оно позволяет проанализировать влияние параметров динамической связи и подсистемы инструмента на устойчивость. В частности, если в (2) а = 0, то условие устойчивости, определяется требованием: h 1 1 >  2 T 1 a 1 ( U - X^ . В этом случае, при прочих неизменных условиях, существует предельное значение глубины внедрения, при котором система теряет устойчивость. Она увеличивает запас устойчивости и при возрастании скорости резания, влияющей на величину запаздывающего аргумента T ₁ .

Пример анализа устойчивости и формирования стационарных многообразий в окрестности равновесия. В качестве примера на рис. 2 показана область устойчивости в параметрическом пространстве. Для наглядности при вычислении областей устойчивости в динамической модели принято: T 2 = 1,5 7 1 .

[ h ] =

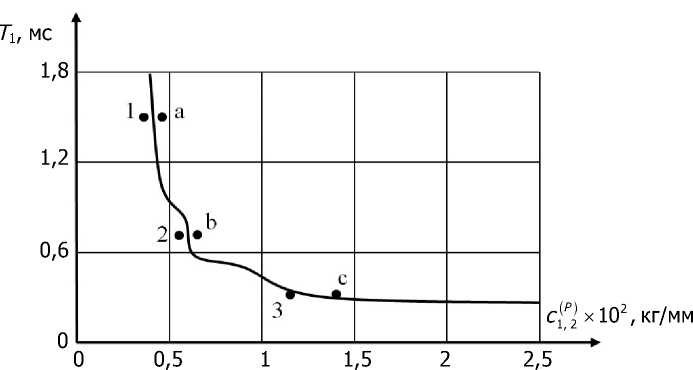
Рис. 2. Область устойчивости системы в параметрическом пространстве

Параметры динамической подсистемы инструмента: [ т ] =

3,2 ■ 10 - 4

кг ■ с²

мм

3,2 ■ 10 - 4

кг ■ с²

мм

0,09кг^с мм

0,02кг^с мм

_ кг ■ с		. кг
0,02---с	202 кг	- 150 —
мм ; [ с 1 =	мм	мм
„ , кг ■ с	, кг	кг
0,1---с	- 150 —	801 кг
мм ]	мм	мм

Рассматриваемая система имеет две основных резонансных частоты: ш _0д = 0,8 кГц и w ₀,₂ = 1,5 кГц . Кроме этого, на рис. 2 обозначено С Р^ = 2 a 1 [ U - X 1 ] — жёсткость процесса резания в направлении X 1 . Жёсткость процесса резания в направлении X 2 принята с 1 ^{( Р} = 0,5^ 1 ) . На иллюстрации точки 1, 2, 3 находятся в области устойчивости, а точки a, b, c — в области неустойчивости. Как видно, существуют некоторые критические значения жёсткости процесса резания и величин запаздывающих аргументов, при которых система является абсолютно устойчивой. Эти значения на рисунке приведены в виде точечных прямых. В том же случае, если параметры соответствуют неустойчивым точкам равновесия, то в их окрестности формируются устойчивые многообразия, для анализа которых необходимо рассматривать исходную систему (3) с учётом нелинейных связей.

Выполненное цифровое моделирование системы (3) с учётом нелинейности динамической характеристики процесса показали, что наиболее типичным при алмазном выглаживании является формирование орбитально-асимптотически устойчивых предельных циклов (рис. 3). В этом случае при переходе от точки 2 к точке b на рис. 2 наблюдается бифуркация Андронова-Хопфа. Однако в некоторых случаях формируются и двумерные инвариантные торы. При этом асимптотически устойчивая точка равновесия (точка 1 на рис. 2) преобразуется в двумерный инвариантный тор (точка а). На приведённых иллюстрациях (рис. 3) показаны: траектории в плоскости « X ₁ — X ₂ » (верхние левые иллюстрации); проекции фазовых траекторий на плоскость « X ₁ — dX ₁ Idt » (верхние правые иллюстрации); проекции фазовых траекторий на плоскость « X ₂ — dX ₂ / dt » (нижние левые иллюстрации); временные траектории (нижние правые траектории). Формируемые многообразия в динамической системе оставляют регулярные следы на поверхности заготовки. Пример их фотографии приведен на рис. 4.

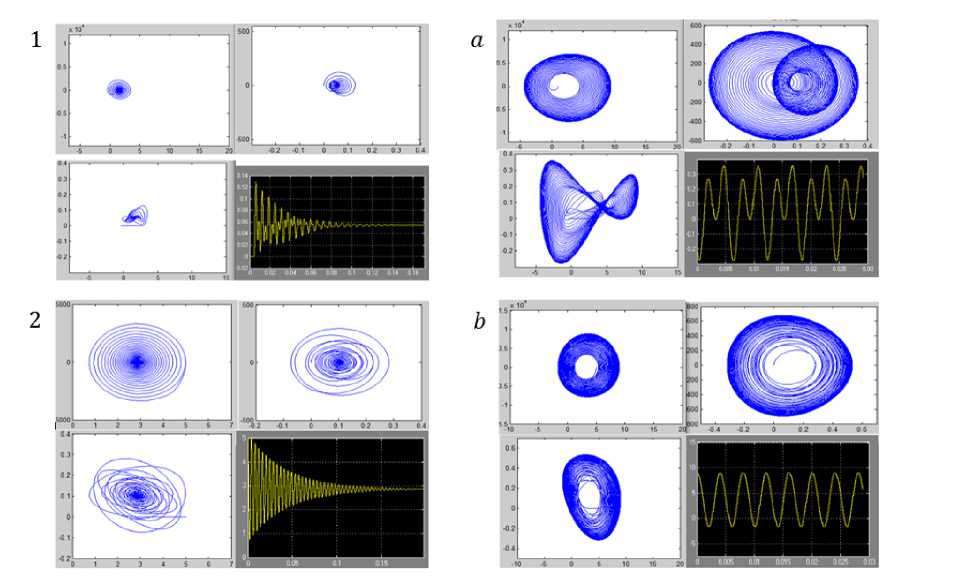
Рис. 3. Стационарные многообразия: 1, 2 — асимптотически устойчивые точки равновесия; а — двумерный тор; b — предельный цикл (одночастотные автоколебания)

Рис. 4. Пример макрорельефа формируемой поверхности в процессе выглаживания в случае, когда инструмент теряет устойчивость точки равновесия и в системе формируются устойчивые автоколебания

Заключение.

• 1.    По своей природе динамическая система процесса выглаживания является аналогичной системе трения интентора относительно образца. Однако рассматриваемый процесс осуществляется в условиях больших контактных нагрузок и значительных пластических деформаций поверхностного слоя обрабатываемой заготовки. Поэтому потеря устойчивости траекторий движения инструмента относительно заготовки является типичной, но недопустимой исходя из цели повышения качества обрабатываемой поверхности.

• 2.    Условия устойчивости принципиально зависят от параметров подсистемы инструмента. Здесь главное значение имеет матрица жёсткости. Поэтому первое направление обеспечения устойчивости процесса связано с установлением рациональных упругих элементов между наконечником и корпусом инструмента. Кроме этого, большое значение имеет ориентация эллипсов жёсткости подсистемы инструмента в плоскости, нормальной к оси вращения заготовки. Ориентация эллипса жёсткости определяется конструктивными свойствами упругих элементов, установленными между алмазным наконечником и корпусом инструмента.

• 3.    На устойчивость принципиально влияет внешнее усилие, зависящее от координаты X ₀ . Во всех случаях, при увеличении этого усилия, система становится более склонной к потере устойчивости. На потерю устойчивости также оказывают влияние запаздывающие аргументы, которые уменьшаются по мере увеличения скорости обработки.

• 4.    Обнаружено, что на устойчивость процесса оказывает влияние радиус сферы алмазного наконечника. Если радиус сферы больше расстояния от поверхности инструмента до центра его вращения, то в системе формируется положительная обратная связь, существенно ухудшающая условия устойчивости системы. Поэтому существует компромисс между желанием увеличить радиус, исходя из требований повышения качества поверхности, и повышением склонности системы к потере устойчивости. В условиях наших исследований рациональный радиус сферы алмазного наконечника равен 4,5 мм.

• 5.    Приведённые математические модели и методика анализа позволяют на стадии проектирования определять технологические параметры и усилие прижима инструмента к заготовке, при которых процесс алмазного выглаживания имеет асимптотически устойчивые проектируемые траектории формообразующих движений.