Устойчивость сегментов тороидальных оболочек при изменении угла отклонения от вертикальной оси
Автор: Бакусов П.А., Семенов А.А.
Статья в выпуске: 3, 2017 года.
Бесплатный доступ
В работе исследуется устойчивость панелей стальных тороидальных тонкостенных оболочечных конструкций с различным углом отклонения от вертикальной оси. Математическая модель (модель Тимошенко-Рейснера) является геометрически нелинейной и представлена в виде функционала полной потенциальной энергии деформации. Для сведения вариационной задачи к решению системы алгебраических уравнений применялся метод Ритца, для которого использовались два различных базиса: тригонометрический и полиномиальный (основан на многочленах Лежандра). Процесс формирования аппроксимирующих функций рассмотрен подробно с учетом симметрии тороидальных панелей. Полученная в итоге система алгебраических уравнений является нелинейной и решается методом Ньютона. Алгоритм реализован в среде аналитических вычислений Maple 2017. Проведены расчеты сегментов тороидальных оболочек при действии внешней равномерно распределенной поперечной нагрузки, и получены значения нагрузок потери устойчивости. При выборе вариантов конструкций фиксировался параметр большого радиуса для того, чтобы покрывная площадь рассматриваемого сегмента оболочки оставалась неизменной, а малый радиус зависел от угла отклонения от вертикальной оси. В ряде случаев наблюдаются местные потери устойчивости. Проанализировано влияние угла отклонения от вертикальной оси на значения нагрузок потери устойчивости и максимальные значения прогибов. Приводятся результаты, полученные для двух видов аппроксимации. Расчеты показали, что оба варианта аппроксимации дают достаточно близкие результаты при малых нагрузках, однако существенно различаются при больших. Увеличение угла отклонения приводит к уменьшению значения критической нагрузки, что может быть вызвано увеличением площади поверхности самой оболочки. Однако при этом уменьшается величина максимального прогиба.
Устойчивость, оболочки, математическая модель, тороидальные оболочки, панели, метод ритца, многочлены лежандра, критические нагрузки
Короткий адрес: https://sciup.org/146211688
IDR: 146211688 | УДК: 539.3 | DOI: 10.15593/perm.mech/2017.3.02
Текст научной статьи Устойчивость сегментов тороидальных оболочек при изменении угла отклонения от вертикальной оси
PNRPU MECHANICS BULLETIN
Изучение поведения оболочечных конструкций имеет существенное значение для различных областей промышленности, в том числе строительства и машиностроения: в строительстве такие конструкции зачастую применяются, например, для покрытия большепролетных сооружений.
Тороидальные оболочки представляют собой один из наиболее сложных видов оболочечных конструкций [1–3], и характер их поведения под действием различных нагрузок изучен еще недостаточно полно. Некоторые исследования в данной области можно найти в работах [4–33].
Устойчивость тороидальных оболочек при статическом нагружении рассматривается в работах [8–9, 12–17, 22, 25–29], при динамическом нагружении – в исследованиях [20– 21, 28–29], а в статьях [4–8, 21] анализируются их колебания. Вопросы оптимизации тороидальных оболочек для решения конкретных практических задач были затронуты в работах [11–12].
Часто для повышения жесткости тороидальные оболочки подкрепляются ребрами жесткости. Исследования таких конструкций можно найти в работах [19–23].
Поведение конструкций при наличии начальных несовершенств рассматривалось в [9, 10, 15–18, 20].
В ряде работ используются уравнения в смешанной форме [18–22], в работах [24–25] учитывается физическая нелинейность, что также представляет большой интерес.
Наиболее полные и обширные исследования с учетом множества различных факторов представлены в статьях [5, 9, 20–21, 25].
Так, например, в работе D.H. Bich и D.G. Ninh [20] исследуются трехслойные подкрепленные тороидальные оболочки, имеющие несовершенства. Используется теория оболочек Кармана–Донелла, анализируется устойчивость при динамическом нагружении, вызванном внутренним течением жидкости.
Работа А.И. Демидова [25] посвящена определению напряженно-деформированного состояния оболочек произвольной формы на основе теории малых упругопластических деформаций, притом геометрические соотношения приняты в линейной постановке. Приводятся результаты численного расчета тонкой незамкнутой тороидальной оболочки при действии нормальной равномерно распределенной нагрузки, когда внутренний и наружный края оболочки абсолютно жестко заделаны, а боковые стороны закреплены шарнирно. Представлены поля интенсивности касательных напряжений по толщине оболочки, установлено значение нагрузки, при которой возникают первые пластические деформации.
Почти во всех рассмотренных работах исследуются тороидальные оболочки, обычно представляющие собой либо полностью замкнутый тор, либо его сегмент, но тоже замкнутый. Исследований, связанных с расчетами панелей тороидальных оболочек, авторам данной статьи найти практически не удалось.
Целью данной работы является анализ устойчивости сегмента тонкостенной тороидальной оболочечной конструкции в зависимости от угла наклона относительно вертикальной оси.
-
1. Теория и методы
-
1.1. Геометрия тороидальной поверхности
-
Вначале рассмотрим тороидальную поверхность. На рис. 1 представлены необходимые для построения тора параметры, а именно: α – угол разворота в плоскости x 0 z , b – угол разворота в плоскости x 0 y , ϕ – угол отклонения относительно оси 0 z , r – малый радиус тора, d – отступ от оси 0 z . Системы координат будут описаны далее.
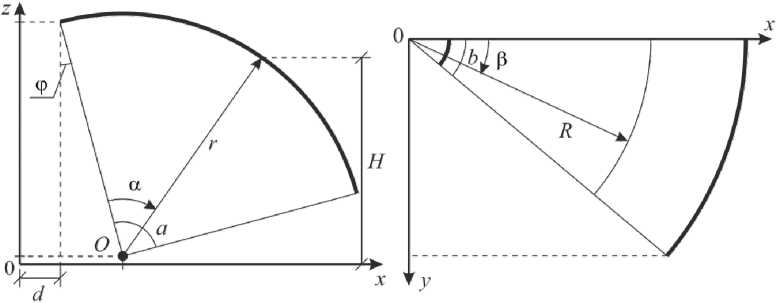
Рис. 1. Проекции тороидальной поверхности на плоскости x 0 z и x 0 y Fig. 1. Projection of a toroidal surface on the x 0 z and x 0 y planes
Используя проекции тора на оси 0 x , 0 y и 0 z , можно получить параметрическое задание тороидальной поверхности:
x — R cos ( р ) — ( d + r sin ( ф ) + r sin ( а-ф ) ) cos ( р ) ,
< y — R sin ( P ) = ( d + r sin ( ф ) + r sin ( а-ф ) ) sin ( р ) , (1)
z — H — r ( 1 - cos ( ф ) + cos ( а-ф ) ) .
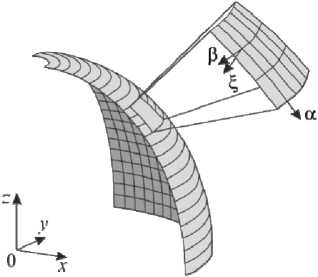
Рис. 2. Глобальная и локальная системы координат Fig. 2. Global and local coordinate systems
На рис. 2 представлены глобальная (0 xyz ) и локальная ( а и р - криволинейные координаты на поверхности, £ - вектор нормали) системы координат.
Используя теорию дифференциальной геометрии [34], нетрудно получить необходимые характеристики поверхности, а именно параметры Ляме (отвечающие за масштабирование)
A — r , B — d + r ( sin ( ф ) + sin ( а-ф ) ) , (2)
а также главные кривизны (отвечающие за геометрию поверхности)
1 k sin ( а-ф )
r’ р d + r ( sin ( ф ) + sin ( а-ф ) )
Полученные выражения для параметров Ляме и главных кривизн будут использованы далее в соотношениях математической модели деформирования оболочечной конструкции.
-
1.2. Математическая модель
Будем рассматривать геометрически нелинейный вариант модели Тимошенко– Рейснера, которая состоит из трех групп соотношений:
-
1) связь деформаций и перемещений – геометрические соотношения;
-
2) связь напряжений и деформаций – физические соотношения;
-
3) функционал полной потенциальной энергии деформации оболочки.
-
1. 2.1. Геометрические соотношения
Для начала рассмотрим геометрические соотношения на срединной поверхности.
Углы поворота нормали вдоль направлений а и в соответственно вычисляются так:
6 а
^^^^н
1 д W
--+ к U A да а
1 а W , , I ---+ kV . B др в J
Связь деформаций через перемещения между рассматриваемыми точками):
_ 1 д и 1 д a 1- 2
1 A да AB др а 2 а
(относительное удлинение элемента дуги
1 д V 1 д в 1 2
8? —---1--- U — kW + 6 ;
2 в др AB да р 2 р
Y 12 =
1 д V 1 д U --+--
_LдЛ +d Bv |+e о , A да B др AB (др да J а₽
Y 13 = kf ( 2 ) ( Та—Оа ) , y 23 = kf ( 2 ) ( Т₽—O₽ ) ,
где k = 5/ 6, a f ( 2 ) - функция, принимающая вид
(1 f (2) = 6 -
( 4
h 2
J
Модель Тимошенко-Рейснера связывает срединный и отстоящие от срединного на 2 слои следующими выражениями:
U 2 = U + 2Та ; V 2 = V + 2Тр ; W 2 = W , (6)
где Та и Тр - углы отклонения волокон от нормали.
Деформации для слоя, отстоящего от срединного на 2 , тогда будут выражаться соотношениями
е ^ =е - + 2Хр ^ 2 = е 2 +^ ; Y ^ 2 =Y i2 + 2X 12 , (7)
где Х 1, Х 2 и х 12 — функции изменения кривизн и кручения,
1 дТа 1 д A 1 дТ 1 д Bш
=-- - +--Т»; х. =--- +--Т.;
A да AB др в 2 B др AB да а
1 дТ.+1 -1" ' (S A Т +6 B Т
A да B др AB (др а да в
-
1.2.2. Физические соотношения
Будем рассматривать задачу в линейно-упругой постановке, тогда физические соотношения (связь напряжений и деформаций) для изотропного материала принимают вид
E /2 2V
^а , 2 (е1 + ц^2); ^р .
1 — Ц
;
E 2 E E
Т 12 = 2(17 ^ ) Y 12 ; Т 23 = 2(17 ^ ) Y 23 ; Т 13 = 2(1 +ц ) Y 13.
где E - модуль упругости, а ц - коэффициент Пуассона.
-
1.2.3. Усилия и моменты
Проинтегрировав соотношения (9) по 2 в пределах от — h /2 до h /2, получим усилия и моменты, приходящиеся на единицу длины сечения:
Eh Eh Eh
N а = -—т(£1 +ц £2 ); N в = -—г(£2 +ц £1 ); N оз—— ;Y 12 ;
1 — ц 1 — ц 2(1 + ц )
Eh 3 Eh 3 Eh 3
M a = 27( X i + ЦХ 2 ); M p = 27( 1 2 +ИХ 1 ); M a p = X 12 ; (ii)
12(1 — ц ) 12(1 — ц ) 24(1 + ц )
Q - = 2 т +ц"lv li:; Q » = 1^ I T 6 )- (12)
На рис. 3 представлены усилия и моменты, приведённые к срединной поверхности.
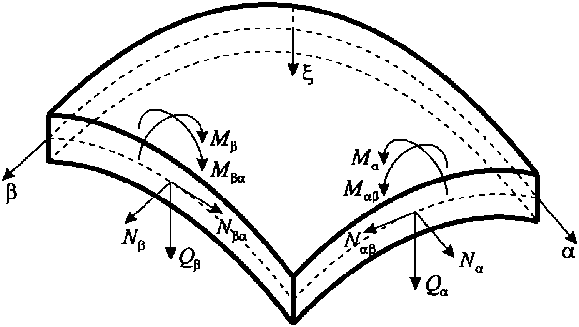
Рис. 3. Усилия и моменты, приведённые к срединной поверхности оболочки
Fig. 3. The efforts and moments reduced to a median surface of the shell
-
1. 2.4. Функционал полной потенциальной энергии деформации
Функционал полной потенциальной энергии деформации представляет собой разность работ внутренних и внешних сил, который при действии внешней равномерно распределенной нагрузки можно записать в виде
1 ab
Ep = 9 JJ [ N “£ 1 + N e8 2 + N 03 ^ 12 + M a X 1 + M p X 2 + M a PX 12 +
2 00 (13)
+ Q ,1 T. 6) ■ Qe (Tp — 6p) — 2 qW ] ABdadp.
Также исходя из условия минимума этого функционала при необходимости можно получить уравнения равновесия.
-
1.3. Алгоритм исследования
-
1.3.1. Метод Ритца
-
Поскольку минимум функционала (11) аналитически найти не представляется возможным, применим один из классических методов минимизации – метод Ритца.
Минимизирующие функции U , V , W , Ta , Tp будем искать в виде линейной комбинации аппроксимирующих функций: nn nn nn
U = ££UjXi(a)13j(p), V = ££v,X2(a>y,-(₽), W = ££WjX3(a)r/(P), i =1 j =1 i=1 j=1 i =1 j =1
nn nn
т Ц ^.iX4 WOT, т, = У £ v,. x5 W (в).
i = 1 j = 1 i = 1 j = 1
Здесь n - количество используемых в разложении базисных функций вдоль каждого направления а и , .
Коэффициенты utj , v9 , wy , уа i. и V , i. являются неизвестными. Для их поиска необходимо найти градиент функционала (13) и приравнять его к нулю.
V E P
ae ae ae ae ae ppp p p auy ’ aVj ’ aWy ’ а^аM ’ а^рa
= 0, i , j = 1, n .
Система (14) является системой алгебраических уравнений с 5 n 2 неизвестными.
-
1.3.2. Выбор аппроксимирующих функций
Как было сказано ранее, для метода Ритца необходимо иметь систему базисных (аппроксимирующих) функций, которые должны удовлетворять граничным условиям, вытекающим из уравнений равновесия. Вводя область D = {( а , , ) : 0 < а < а , 0 < , < b} , в которой мы рассматриваем поставленную нами задачу, граничные условия можно записать следующим образом:
U |g D = 0 ^ X 1 (0) = X 1 ( а ) = Y (0) = Y 1 ( b ) = 0, (15а) V |а D = 0 ^ X 2 (0) = X 2( а ) = Y 2 (0) = Y 2 ( b ) = 0, (15б) W |g D = 0 ^ X з (0) = X з ( а ) = Y 3 (0) = Y 3 ( b ) = 0, (15в)
Т^ = Tj ₽ = ь = 0 ^ Y 4 (0) = Y 4 ( b ) = 0 , (15г) тв L= 0 = T' L= а = 0 ^ X 5 (0) = X 5 ( а ) = 0 . ( 15 д)
Поскольку закрепление контура конструкции было выбрано шарнирно-неподвижное, кроме условий (15в)-(15д), также должны выполняться следующие условия:
|
a 2w da 2 |
2 = --r = 0 ^ X з (0) = X з ( а ) = Y 3 (0) = Y 3 ( b ) = 0, (16а) d D de d D ат ат __« =__« = 0 ^ X 4 (0) = X 4 ( а ) = 0 (16б) da a= 0 da a= а атв ат -Ji- =^- = 0 ^ Y , (0) = Y , ( b ) = 0. (16в) дв , ь |
В данной работе нами было рассмотрено два базиса: тригонометрический и полиномиальный. Используя тригонометрический бизис, функции перемещений представим в виде
n n f a i
U = УУ uy sin I in— I sin i=1 j=1 V а j nn
V = 22
i = 1 J" = 1
■ Г • a ) ■ Г ■ в) v. . sin i n sin j n , ij
V a ) V b )
nn
W 22
i = 1 J = 1
• Г- a ) • Г - в) w,, sin i П sin J П , ij
V a ) V b )
Г a) ГR)
^a=V\ua cos in sin Jn a 1=1 ^V a) V n^ Г. a) Гв)
V=T У и sin in cos J П
₽ д_д_ \<.
Для описания полиномиального базиса сначала введём стандартизированные многочлены Лежандра на интервале ( - 1;1) [35]. Отличие этих многочленов от обычных многочленов Лежандра заключается в том, что на краях интервала они принимают значения ± 1. Формула получения стандартизированного полинома Лежандра степени к представлена ниже:
P k ( t ) =
1 dk k !2 kdtk
( t 2 - 1) к , к = 0,1,...
Для перехода от интервала ( - 1;1) к интервалу ( s 0; s ) можно воспользоваться простой заменой переменных:
2( t - s о) _ X — 1.
s - s о
Первые пять стандартизированных многочленов Лежандра Pk ( t ) представлены ниже:
32 1 53 3 35 415 23
1 о ( 1 ) ; 1( t ) t ; 2( t ) 2 t 2 ; 3( t ) 2 t 2 t ; 4 ( t ) 8 t 4 t + 8 .
На рис. 4, а представлены графики этих функций.
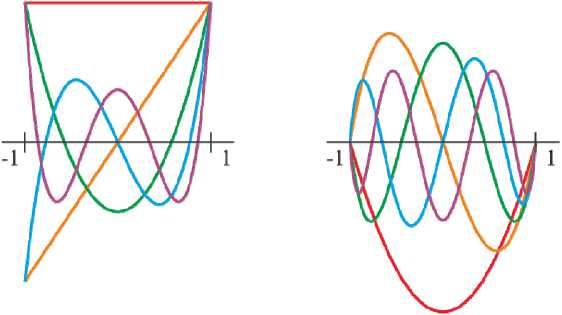
а б
Рис. 4. Графики аппроксимирующих функций: a – стандартизированные многочлены Лежандра; б – многочнены Kn ( t )
Fig. 4. Graphs of approximating functions: а – are standardized
Legendre polynomials; b – are Kn ( t ) polynomials
Для того чтобы удовлетворить условиям (15а) и (15б), из многочленов (18) построим полиномы Kn ( t ) [36], которые на концах рассматриваемого промежутка будут принимать нулевые значения. Они будут задаваться формулой
K n ( t ) = P n + 1 ( t ) - P n - 1 ( t ), n = 1,2,.... (19)
Первые пять разностных многочленов Kn ( t ) представлены ниже, а их графики показаны на рис. 4, б .
33 55 35 21 7
K ( t ) = -t 2 ; K ( t) = -t 3 1 ; K ( t ) = 1 4-- 1 2 +- ;
n 22 n 22 n 848
63 45 27 231 385 165 11
K ( t ) = —t 5-- t 3 +— t ; K ( t ) = —t 6-- t 4 +— t 2 - .
n 848 n 15 16 16 16
Для выполнения условий (15г) и (15д), а также условия, накладываемого на первую производную в (16б) и (16в), построим многочлены Kn * ( t ) вида
K(t) = P+----P»L, n (n + 2)( n + 3) n (n +1)
n = 1,2,....
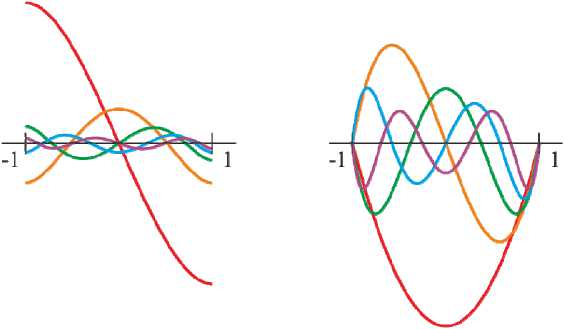
Первые пять многочленов Kn *( t ) представлены ниже, а их графики и графики их первой производной показаны на рис. 5.
25 77 49 21 1 3
к „( t ) = —t 3 — t ; k „( t ) = —t 4 — t 2 + ; k „( t ) = —t 5 — t 3 + -t ;
n 24 8 n 32 16 480 n 80 2 6
11 11 11
к ( t ) = —t 6 — t 4 +— t7
n 32 16 32
11 * 429 7 663 5 247 3 13
----- ; K ( t ) ----- t--t +-- t--t
420 n 896 640 384 128
а б
Рис. 5. Графики аппроксимирующих функций: a – многочлены Kn * ( t );
б – первая производная многочленов Kn * ( t )
Fig. 5. Graphs of approximating functions: а – are Kn * ( t ) polynomials;
b – is the first-order derivative of Kn * ( t ) polynomials
Наконец, чтобы удовлетворить условиям (15в) и (16а), используя разностные многочлены Kn ( t ), построим многочлены Kn **( t ) вида
C( t ) =
n ( n + 1)(2 n + 1)
( n + 2)( n + 3)(2 n + 5)
K n + 2 ( t ) - K n (t ),
n = 1,2,....
Первые пять многочленов Kn **( t ) представлены ниже, а их графики и графики их второй производной показаны на рис. 6.
„ 5 4 15 , 25 „ 21 < 35 . 49
K * ( t ) = — t 4 - 15 t 2 + 25 ; K * ( t ) = 21t 5 - 35t 3 + 49 t ;
n 16 8 16 n 16 8 16
147 21 63
„ ( t ) = t 6-- t 4 + t1
n 40 2 8
-
20 ;
495 99 165 33
K„ ( t ) =----- t 7-- t 5 +---- t 3-- 1 ;
n 56 4 8 7
„ 70785 s
K* *( t) = 7078518 n3584
------16 +
-
2145 2 3289
----------1 +.
128 3584
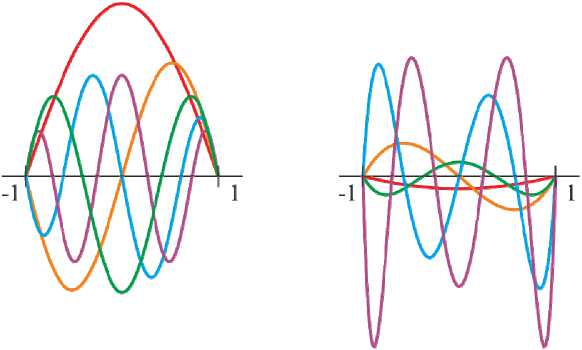
а б
Рис. 6. Графики аппроксимирующих функций: a – многочлены Kn ** ( t ); б – вторая производная многочленов Kn ** ( t )
Fig. 6. Graphs of approximating functions: а – are Kn ** ( t ) polynomials; b – is the second-order derivative of Kn ** ( t ) polynomials
В итоге, введя многочлены Kn ( t ), Kn *( t ) и Kn **( t ), функции перемещений можно записать следующим образом:
nn
U = EZ u«Ki(a) K/P)
i = 1 i = 1
nn
V = ZZ v « K . ( a ) K j* )
i = 1 j = 1
nn
W = ZZ w ,j K'*( a ) K '(P )
i = 1 j = 1
nn
nn
*l = EE » < j K i ( “ ) K ‘ ( P )- i = 1 j = 1
Стоит отметить, что в зависимости от геометрии оболочки можно брать не все базисные функции. Например, для тороидальной панели в ходе численного эксперимента было выявлено, что рациональнее всего использовать следующие комбинации аппроксимирующих функций:
nn nn nn
U = SSugXl4a№2j-,(P), V = ZZv X2(a H (в,, W У Уw,X3(a )i (,), i =1 j=1 i=1 j=1 i=1 j=1
nn nn
* a = ZZ V a X 4 i a , ; ( в ). V , = ££ v , X\ ( a ) > ■ ( ,). i = 1 j = 1 i = 1 j = 1
Такие выводы были сделаны на основе того, что тороидальная панель обладает симметрией в направлении оси , , и значения коэффициентов при «исключенных» элементах оказались близки к нулю. Таким образом, эти функции вносили крайне малый вклад в точность расчета.
-
1.3.3. Метод Ньютона для решения СНАУ
-
2. Расчеты
Система (14), полученная в пункте 1.3.1, является нелинейной алгебраической системой от 5 n 2 переменных. В общем случае аналитически такая система не решается, поэтому для поиска неизвестных был выбран метод Ньютона для СНАУ.
Обозначим за X = { u j , v , , w , , у a i , у ь , }, i , j = 1, n набор искомых переменных, а за X 0 = 0 - нулевое приближение. Тогда каждое последующее приближение X , + 1 будет выражаться через предыдущее по формуле
X,+1 = Xn -H-1 (X, )VEp (X,), где H – это матрица Гессе функционала Ep .
Задав необходимую точность а, процесс вычисления приближений можно остановить при удовлетворении условия maxl X,+1 - X,| <а .
В данной работе при проведении расчетов рассматривается последовательное нагружение панели, поэтому после нахождения решения X N системы (14) для нагрузки qN за нулевое приближение X 0 + 1 для следующего нагружения qN + 1 = qN + A q принимается решение X N .
Предложенный алгоритм был реализован в среде аналитических вычислений Maple 2017.
Будем рассматривать панель стальной ( E = 2,1 • 10 5 МПа, ц = 0,3) тороидальной оболочки, закрепленную шарнирно-неподвижно, используя два вида аппроксимации: тригонометрическую и полиномиальную. Количество слагаемых в разложениях функций в методе Ритца N = , 2 = 9 . Нагрузка - нормально-распределенная, приложенная со стороны выпуклости.
Размеры панели следующие: a = b = п /2 рад, d = 2 м, толщина h = 0,01 м. Большой радиус R = 15 м, притом при выборе вариантов конструкций этот параметр фиксируется для того, чтобы покрывная площадь рассматриваемого сегмента оболочки оставалась неизменной (173,5 м2). При этом малый радиус r становится переменным и зависит от угла ф :
sin( a — ф ) + sin( ф )
Угол отклонения от вертикальной оси ф берётся различным, в зависимости от рассматриваемого варианта (табл. 1):
Таблица 1
Рассматриваемые варианты
Considered variants
Table 1
|
Параметр |
Номер варианта |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
ф , рад |
0 |
п |
2 п |
3 п |
4 п |
5 п |
6 п |
7 п |
|
28 |
28 |
28 |
28 |
28 |
28 |
28 |
||
|
r , м |
13 |
11,75 |
10,85 |
10,20 |
9,73 |
9,42 |
9,25 |
9,19 |
Вначале рассмотрим подробно вариант 1. На рис. 7 показана полученная зависимость прогиба W от нагрузки q при тригонометрической (рис. 7, а ) и полиномиальной (рис. 7, б ) аппроксимации.
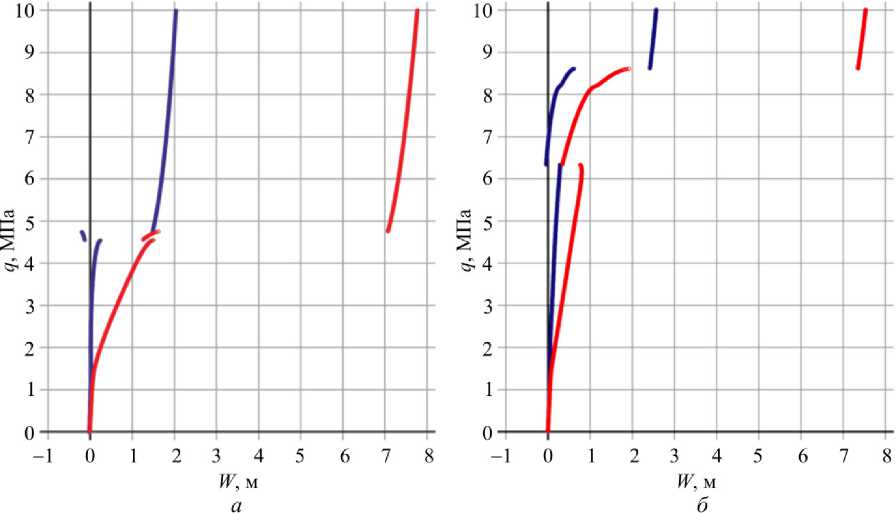
Рис. 7. Графики зависимости прогиба W от нагрузки q в середине W ( a /2, b /2) (красный) и в четверти W ( a /4, b /4) (синий) панели при ( а ) – тригонометрической и ( б ) – полиномиальной аппроксимации
Fig. 7. Stress-strain curve in the middle W ( a /2, b /2) (red) and in a quarter (blue) of the panel at trigonometric ( а ) and polynomial ( b ) approximations
На рис. 8 и 9 показаны поля прогибов до и после потери устойчивости, отложенные на тороидальной оболочке.
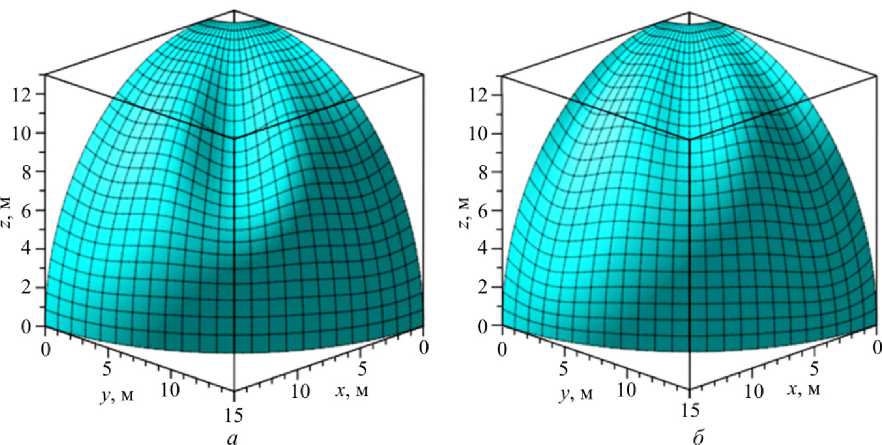
Рис. 8. Поле прогибов до потери устойчивости, отложенное на панели тороидальной оболочки при ( а ) – тригонометрической и ( б ) – полиномиальной аппроксимации для варианта 1 Fig. 8. The deflection field before the loss of stability which is effected on the panel of the toroidal shell during trigonometric ( a ) and polynomial approximations ( b ) for variant 1
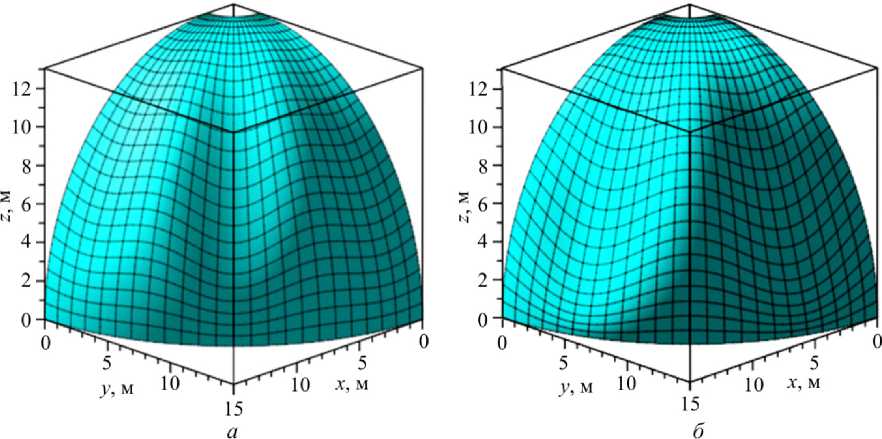
Рис. 9. Поле прогибов после потери устойчивости, отложенное на панели тороидальной оболочки при ( а ) – тригонометрической и ( б ) – полиномиальной аппроксимации для варианта 1 Fig. 9. The deflection field after the loss of stability effected on the panel of the toroidal shell at trigonometric ( a ) and polynomial ( b ) approximations for variant 1
Для варианта 4 поля прогибов до и после потери устойчиости, отложенные от панели тороидальной панели, представлены на рис. 10 и 11.
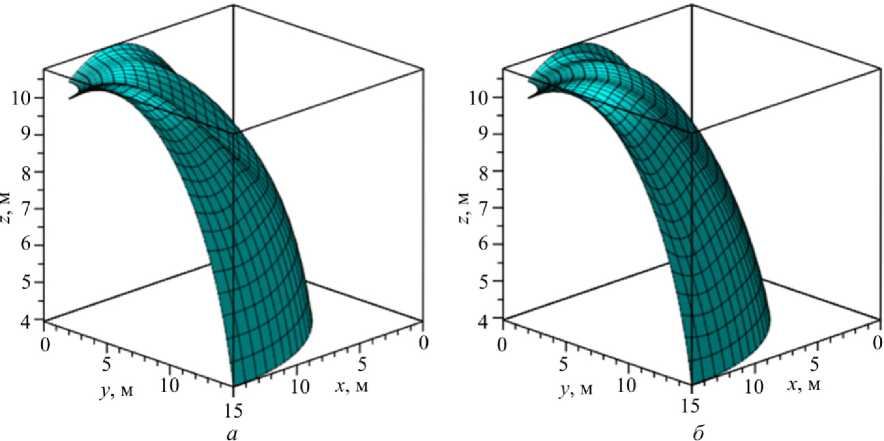
Рис. 10. Поле прогибов до потери устойчивочти, отложенное на панели тороидальной оболочки при ( а ) – тригонометрической и ( б ) – полиномиальной аппроксимации для варианта 4 Fig. 10. The deflection field before the loss of stability which is effected on the panel of the toroidal shell at trigonometric ( a ) and polynomial ( b ) approximations for variant 4
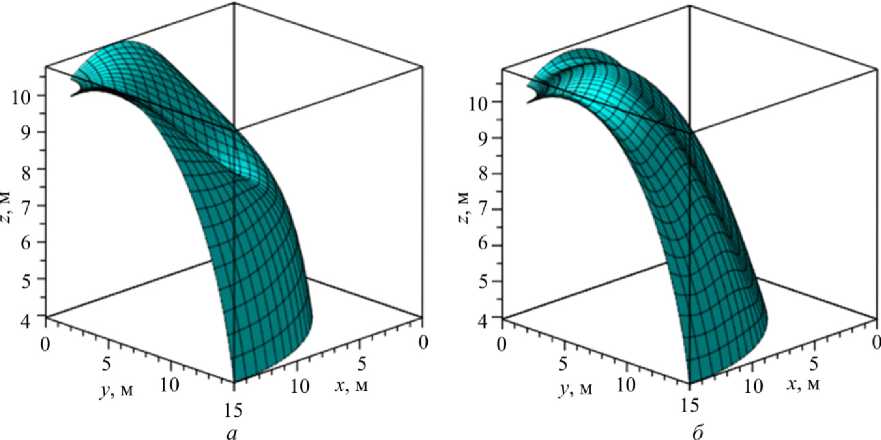
Рис. 11. Поле прогибов после потери устойчивости, отложенное на панели тороидальной оболочки при ( а ) – тригонометрической и ( б ) – полиномиальной аппроксимации для варианта 4 Fig. 11. The deflection field after the loss of stability which is effected on the panel of the toroidal shell at trigonometric ( a ) and polynomial ( b ) approximations for variant 4
Критические нагрузки, полученные для всех рассматриваемых вариантов, а также значения максимальных прогибов представлены в табл. 2.
Для большей наглядности, данные из табл. 2 были представлены в виде графиков на рис. 12, и 13. Так как в ряде случаев перед общей потерей устойчивости наблюдалась локальная потеря устойчивости [37], на графиках это показано ветвлением кривой.
Таблица 2
Значения критических нагрузок при различных углах ϕ
The values of the critical loads for various angles ϕ
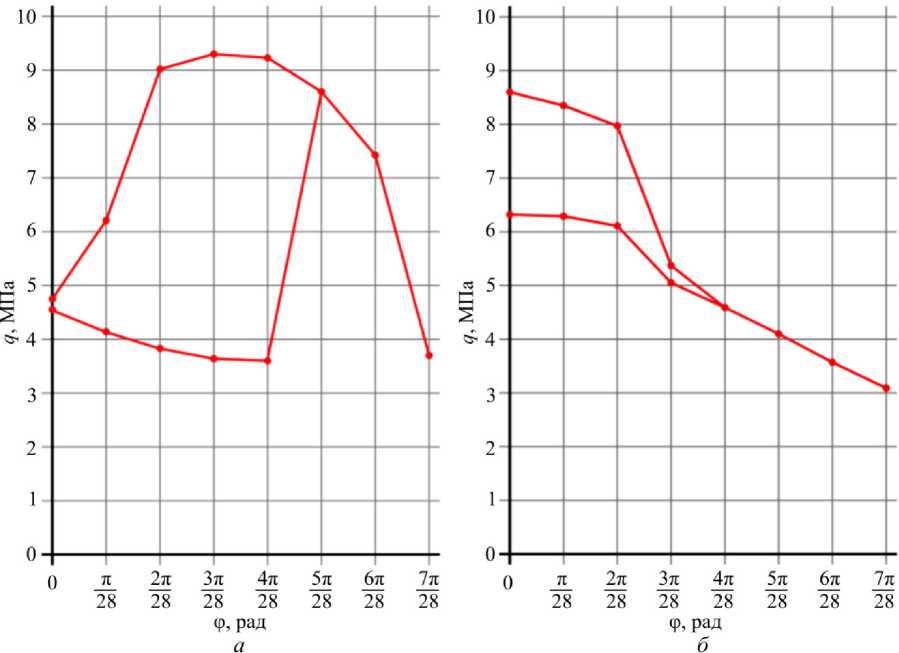
Рис. 12. Графики критических нагрузок в зависимости от угла ϕ при ( а ) – тригонометрической и ( б ) – полиномиальной аппроксимации Fig. 12. Graphs of critical loads deflections depending on the angle ϕ at trigonometric ( a ) and polynomial ( b ) approximations
Table 2
|
Параметр |
Номер варианта |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|
ϕ , рад |
0 |
π |
2 π |
3 π |
4 π |
5 π |
6 π |
7 π |
|
|
28 |
28 |
28 |
28 |
28 |
28 |
28 |
|||
|
Критические нагрузки, М |
Па |
||||||||
|
Триг. |
1 крит. |
4,55 |
4,14 |
3,83 |
3,64 |
3,6 |
8,66 |
7,42 |
3,7 |
|
аппрокс. |
2 крит. |
4,75 |
6,21 |
9,02 |
9,3 |
9,23 |
– |
– |
– |
|
Полин. |
1 крит. |
6,32 |
6,29 |
6,11 |
5,05 |
4,59 |
4,1 |
3,57 |
3,09 |
|
аппрокс. |
2 крит. |
8,6 |
8,35 |
7,97 |
5,37 |
– |
– |
– |
– |
|
Значения максимального прогиба, м |
|||||||||
|
Триг. |
1.5 МПа |
0,1138 |
0,1029 |
0,1019 |
0,1067 |
0,1141 |
0,1213 |
0,1259 |
0,1278 |
|
3 МПа |
0,6565 |
0,5684 |
0,5158 |
0,4819 |
0,4480 |
0,3969 |
0,3302 |
0,2921 |
|
|
аппрокс. |
1 крит. |
1,5735 |
1,3175 |
1,0929 |
0,9715 |
0,9556 |
2,3271 |
1,7049 |
0,7213 |
|
Полин. аппрокс. |
1,5 МПа |
0,1174 |
0,1025 |
0,0984 |
0,0985 |
0,0995 |
0,1002 |
0,1012 |
0,1043 |
|
3 МПа |
0,4568 |
0,3677 |
0,3115 |
0,2752 |
0,2518 |
0,2383 |
0,2351 |
0,3461 |
|
|
1 крит. |
1,0992 |
0,9835 |
0,8295 |
0,5424 |
0,4400 |
0,4124 |
0,4154 |
1,0150 |
|
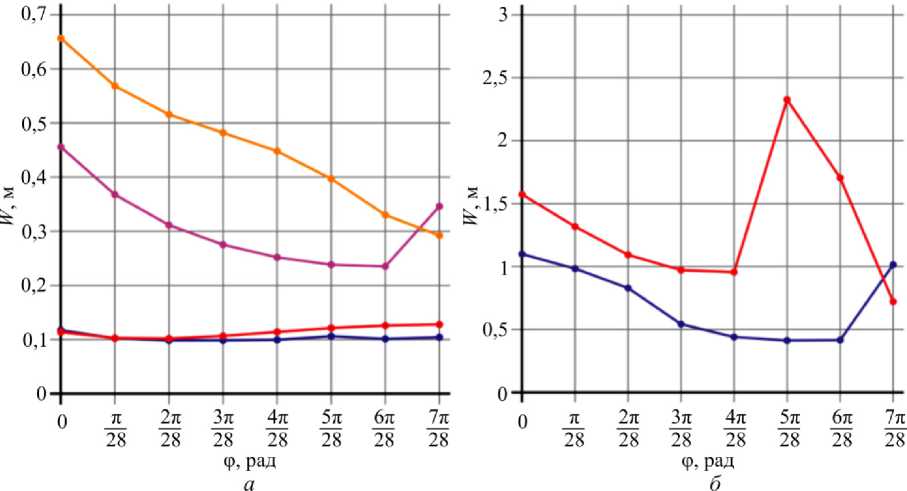
Рис. 13. Графики максимальных прогибов в зависимости от угла ф : а - красный и оранжевый -тригонометрическая аппроксимация, нагрузки q = 1,5 МПа и q = 3 МПа соответственно, синий и фиолетовый - полиномиальная аппроксимация, нагрузки q = 1,5 МПа и q = 3 МПа соответственно; б – нагрузка при потере устойчивости, красный – тригонометрическая, синий – полиномиальная аппроксимации
Fig. 13. Graphs of maximum deflections depending on the angle ф : a the red and orange colors show the trigonometric approximation, the load is q = 1,5 MPa, and q = 3 MPa respectively, the blue and purple colors show the polynomial approximation, the load is q = 1,5 MPa, and q = 3 MPa respectively; b load with the loss of stability, the red color shows the trigonometric approximation, the blue color shows the polynomial approximation
Заключение
Из полученных данных можно сделать следующие выводы:
-
- тригонометрическая аппроксимация не всегда может улавливать локальную потерю устойчивости;
-
- с увеличением нагрузки расхождение между разными вариантами аппроксимаций увеличивается (см. рис. 13);
-
- увеличение угла отклонения ф приводит к уменьшению значения критической нагрузки, что может быть вызвано увеличением площади поверхности самой оболочки;
-
- при увеличении угла ф величина максимального прогиба уменьшается.
Работа выполнена при поддержке Минобрнауки РФ, проект № 9.5605.2017/8.9.
Список литературы Устойчивость сегментов тороидальных оболочек при изменении угла отклонения от вертикальной оси
- A survey of works on the theory of toroidal shells and curved tubes/R. Wenmin //Acta Mechanica Sinica. -1999. -Vol. 15. -No. 3. -P. 225-234 DOI: 10.1007/BF02486150
- Jiammeepreecha W., Chucheepsakul S. Nonlinear static analysis of an underwater elastic semi-toroidal shell//Thin-Walled Structures. -2017. -Vol. 116. -P. 12-18 DOI: 10.1016/j.tws.2017.03.001
- Sun B. Closed-Form Solution of Axisymmetric Slender Elastic Toroidal Shells//Journal of Engineering Mechanics. -2010. -Vol. 136. -No. 10. -P. 1281-1288 DOI: 10.1061/(ASCE)EM.1943-7889.0000175
- Jiang W., Redekop D. Static and vibration analysis of orthotropic toroidal shells of variable thickness by differential quadrature//Thin-Walled Structures. -2003. -Vol. 41. -No. 5. -P. 461-478 DOI: 10.1016/S0263-8231(02)00116-7
- A unified accurate solution for vibration analysis of arbitrary functionally graded spherical shell segments with general end restraints/Z. Su //Composite Structures. -2014. -Vol. 111. -P. 271-284 DOI: 10.1016/j.compstruct.2014.01.006
- Матвеев Е.П. Решение задачи о свободных колебаниях тороидальной оболочки с протекающей жидкостью при различных граничных условиях//Вестн. гражданских инженеров. -2010. -№ 1. -P. 64-67.
- Tizzi S. A free vibration analysis of toroidal composite shells in free space//Journal of Sound and Vibration. -2015. -Vol. 337. -P. 116-134 DOI: 10.1016/j.jsv.2014.10.015
- Redekop D., Muhammad T. Analysis of Toroidal Shells Using the Differential Quadrature Method//International Journal of Structural Stability and Dynamics. -2003. -Vol. 03. -No. 02. -P. 215-226 DOI: 10.1142/S0219455403000860
- An efficient model reduction method for buckling analyses of thin shells based on IGA/K. Luo //Computer Methods in Applied Mechanics and Engineering. -2016. -Vol. 309. -P. 243-268 DOI: 10.1016/j.cma.2016.06.006
- Hutchinson J.W. Initial post-buckling behavior of toroidal shell segments//International Journal of Solids and Structures. -1967. -Vol. 3. -No. 1. -P. 97-115 DOI: 10.1016/0020-7683(67)90046-7
- Truong Vu V. Minimum Weight Design for Toroidal Shells With Strengthening Component//Journal of Pressure Vessel Technology. -2015. -Vol. 138. -No. 2. -P. 021202 DOI: 10.1115/1.4031445
- Skoczeń B. Geometrically nonlinear elastic toroidal shells with open profiles-stability analysis and a design concept//Archive of Applied Mechanics. -1992. -Vol. 62. -No. 1. -P. 1-14 DOI: 10.1007/BF00786677
- Karpov V., Panin А., Kharlab V. Stability of elastic toroid-shape shells//Proceeding of 7th International Conference Contemporary Problem of Architecture and Construction. November 19th -21st, 2015. -Italy. Florence, 2015. -С. 487-490.
- Frikha A., Dammak F. Geometrically non-linear static analysis of functionally graded material shells with a discrete double directors shell element//Computer Methods in Applied Mechanics and Engineering. -2017. -Vol. 315. -P. 1-24 DOI: 10.1016/j.cma.2016.10.017
- Galletly G.D. Buckling of imperfect elastic elliptic toroidal shells subjected to uniform external pressure//Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering. -1999. -Vol. 213. -No. 3. -P. 199-214 DOI: 10.1243/0954408991529933
- Wang A., Zhang W. Asymptotic solution for buckling of toroidal shells//International Journal of Pressure Vessels and Piping. -1991. -Vol. 45. -No. 1. -P. 61-72 DOI: 10.1016/0308-0161(91)90044-3
- Błachut J., Jaiswal O. On buckling of toroidal shells under external pressure//Computers & Structures. -2000. -Vol. 77. -No. 3. -P. 233-251 DOI: 10.1016/S0045-7949(99)00226-6
- Oyesanya M.O. Influence of extra terms on asymptotic analysis of imperfection sensitivity of toroidal shell segment with random imperfection//Mechanics Research Communications. -2005. -Vol. 32. -No. 4. -P. 444-453 DOI: 10.1016/j.mechrescom.2005.02.006
- Dung D.V., Vuong P.M. Nonlinear analysis on dynamic buckling of eccentrically stiffened functionally graded material toroidal shell segment surrounded by elastic foundations in thermal environment and under time-dependent torsional loads//Applied Mathematics and Mechanics. -2016. -Vol. 37. -No. 7. -P. 835-860 DOI: 10.1007/s10483-016-2099-9
- Bich D.H., Ninh D.G. Research on dynamical buckling of imperfect stiffened three-layered toroidal shell segments containing fluid under mechanical loads//Acta Mechanica. -2017. -Vol. 228. -No. 2. -P. 711-730 DOI: 10.1007/s00707-016-1724-0
- Thang P.-T., Nguyen-Thoi T. A new approach for nonlinear dynamic buckling of S-FGM toroidal shell segments with axial and circumferential stiffeners//Aerospace Science and Technology. -2016. -Vol. 53. -P. 1-9 DOI: 10.1016/j.ast.2016.03.008
- Dao B.H., Dinh N.G., Tran T.I. Buckling Analysis of Eccentrically Stiffened Functionally Graded Toroidal Shell Segments under Mechanical Load//Journal of Engineering Mechanics. -2016. -Vol. 142. -No. 1. -P. 04015054 DOI: 10.1061/(ASCE)EM.1943-7889.0000964
- Simplified theoretical solution of circular toroidal shell with ribs under uniform external pressure/Q. Du //Thin-Walled Structures. -2015. -Vol. 96. -P. 49-55 DOI: 10.1016/j.tws.2015.07.019
- Chernyshenko I.S., Maksimyuk V.A. On the stress-strain state of toroidal shells of elliptical cross section formed from nonlinear elastic orthotropic materials//International Applied Mechanics. -2000. -Vol. 36. -No. 1. -P. 90-97 DOI: 10.1007/BF02681963
- Демидов А.И. Упругопластическое напряженно-деформированное состояние тонкой незамкнутой тороидальной оболочки//Современное промышленное и гражданское строительство. -2006. -Т. 2, № 4. -P. 163-176.
- Semenyuk N.P., Zhukova N.B. Stability of compound toroidal shells under external pressure//International Applied Mechanics. -2011. -Vol. 47. -No. 5. -P. 545-553 DOI: 10.1007/s10778-011-0476-8
- Тарасов В.Н., Андрюкова В.Ю. Об устойчивости тороидальной оболочки с односторонним подкреплением//Вестн. Сыктывкар. ун-та. Сер. 1: Математика. Механика. Информатика. -2012. -№ 15. -P. 63-72.
- Nonlinear static and dynamic analysis of hyper-elastic thin shells via the absolute nodal coordinate formulation/K. Luo //Nonlinear Dynamics. -2016. -Vol. 85. -No. 2. -P. 949-971 DOI: 10.1007/s11071-016-2735-z
- Naboulsi S.K., Palazotto A.N., Greer J.M. Static-Dynamic Analyses of Toroidal Shells//Journal of Aerospace Engineering. -2000. -Vol. 13. -No. 3. -P. 110-121. ) DOI: 10.1061/(ASCE)0893-1321(2000)13:3(110
- Parnell T.K. Numerical improvement of asymptotic solutions for shells of revolution with application to toroidal shell segments//Computers & Structures. -1983. -Vol. 16. -No. 1-4. -P. 109-117 DOI: 10.1016/0045-7949(83)90152-9
- Grigorenko Y.M., Avramenko Y.A. Refined Stress Analysis of Orthotropic Toroidal Shells//International Applied Mechanics. -2013. -Vol. 49. -No. 4. -P. 461-474 DOI: 10.1007/s10778-013-0580-z
- Vu V.T., Blachut J. Plastic Instability Pressure of Toroidal Shells//Journal of Pressure Vessel Technology. -2009. -Vol. 131. -No. 5. -P. 051203 DOI: 10.1115/1.3148824
- Asratyan M.G., Gevorgyan R.S. Mixed boundary-value problems of thermoelasticity for anisotropic-in-plan inhomogeneous toroidal shells//Journal of Applied Mathematics and Mechanics. -2010. -Vol. 74. -No. 3. -P. 306-312 DOI: 10.1016/j.jappmathmech.2010.07.006
- Погорелов А.В. Дифференциальная геометрия. -М.: Наука, 1974. -176 с.
- Филимоненкова Н.В. Конспект лекций по функциональному анализу. -СПб.: Лань, 2015. -176 с.
- Ильин В.П., Карпов В.В. Устойчивость ребристых оболочек при больших перемещениях. -M.: Стройиздат, 1986. -168 с.
- Баранова Д.А., Карпов В.В., Семенов А.А. Компьютерное моделирование местных и общих форм потери устойчивости тонкостенных оболочек//Вычислительная механика сплошных сред. -2015. -Т. 8, № 3. -P. 229-244.


