Устойчивость широтно-импульсного стабилизатора в режиме прерывистых токов

В работе [1] предложен метод исследования, позволяющий успешно решать задачи анализа устойчивости и синтеза систем с широтно-импульсной модуляцией. Предложенная методика может быть распространена на случай, когда в широтно-импульсной системе имеется дополнительная существенная нелинейность.

Импульсный стабилизатор напряжения (ИСН) состоит из транзисторного ключа, управляемого широтно-импульсным модулятором (ШИМ), первичного источника напряжения Е и источника опорного напряжения U оп , LC -фильтра ( r – активное сопротивление дросселя), сопротивления нагрузки R и диода, включающегося в работу при закрытии транзисторного ключа (рис. 1). В процессе работы сопротивление нагрузки и напряжение источника изменяются. Система в этом случае может работать в двух режимах: при непрерывном и прерывистом изменении тока дросселя фильтра I ₂. Анализу устойчивости системы в первом случае посвящено достаточно большое количество работ, в частности [1], и методика решения этой задачи известна. Второй, более сложный случай, в литературе рассмотрен только с энергетических позиций. Динамические характеристики этого режима практически не исследованы.

Рис. 1

питания. ШИП генерирует ЭДС Е ШИП , равную Е при открытом ключе и нулю при закрытом.

В этой схеме (см. рис. 2) так же, как и в исходной, напряжение на входе фильтра при условии идеальности характеристик диода в режиме прерывистых токов дросселя U 1 = Е , когда транзисторный ключ открыт; U 1 = 0 при закрытом ключе и I 2 ≠ 0; U 1 = U 2 при I 2 = 0.

Используем далее схему рис. 2. Разложим напряжение Е ШИП в ряд Фурье, ограничившись членами ряда, определяющими постоянную составляющую и первую гармонику. При этом для упрощения выражений без потери достоверности получаемых результатов считаем, что ось ординат проходит посередине импульса. Тогда функция, характеризующая заданную последовательность импульсов, является четной и при разложении в ряд Фурье b K = 0 [2]. Следовательно, в нашем случае надо найти коэффициенты а 0 и а 1 :

1 nT -τ 2

a ₀ =     ∫ Edt = E γ ,

T -τ 2

В данной статье на основе предложенного в [1] подхода к анализу устойчивости систем с широтноимпульсной модуляцией рассматривается устойчивость ИСН в режиме прерывистых токов дросселя I 2 .

Постановка задачи. Схему, изображенную на рис. 1, можно представить в виде гипотетической схемы (рис. 2), в которой широтно-импульсный преобразователь (ШИП) совмещает в себе действия ШИМ, транзисторного ключа и первичного источника

a ₁

2 nT -τ2       2 π

E cos tdt =

TT

-τ 2

2 E

sin πγ , π

где τ – время открытого состояния ключа на периоде следования импульсов; Т – период следования импульсов; γ = τ / Т – относительная длительность импульса. Поскольку τ в процессе работы стабилизатора изменяется во времени, то можно принять, что τ ( t ) и Y ( t ) являются функцией времени.

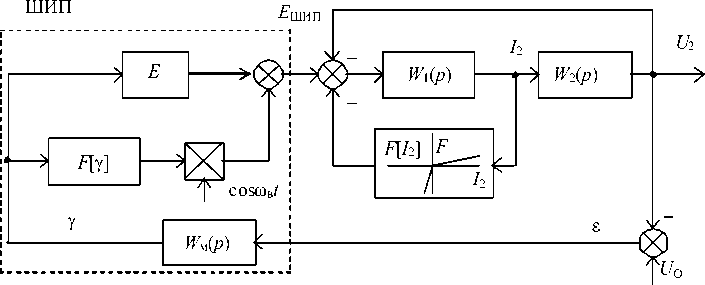
Рис. 3

С учетом вышеизложенного система дифференциальных уравнений, описывающая процессы в стаби лизаторе, примет вид

LI 2 ( t ) = E Y ( t ) + — sin( nY ( t )) cos ⁽ 2 ^П t | - п             I T )

- U ₂( t ) - ri ₂( t ) - F [ 1 ₂( t ) ] ,               (1)

CU 2 ( t ) = 1 2 ( t ) - YU 2 ( t ),

Y(t) = k(UоП - U2(t)) , где Y = 1/R; k - коэффициент передачи модулятора, который в данном случае принят астатическим. На основании (1) строим структурную схему (рис. 3), где передаточные функции W1(p) = 1/(Lp + r), W2(p) = 1/(Cp + Y), WM(p) = k/p, нелинейная функция F[12(t)] определяет нелинейность диодного типа с коэффициентами k1 в открытом состоянии диода, когда

1 ₂ >  0, и к ₂ - в закрытом, F [ у ] = —sin ( лу ( t ) ) . п

Задача исследования устойчивости системы заключается в определении условий возникновения автоколебаний при наличии постоянной составляющей и вынужденных колебаний ю_в. Вынужденные высокочастотные колебания не оказывают воздействия на переменную у , так как значительно ослабляются фильтром и самим модулятором. Решение ищем в виде

I 2 = I 2 ⁺ I 21 ⁺ I 2» , U 2 = U 0 + U 21 + U 2» , Y = Y o + Y 1 ,

Решение (2) ищем в виде

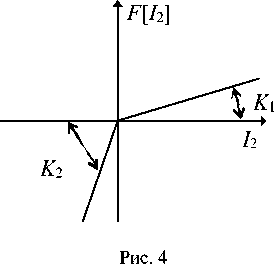
12» = Ав sin (toBt + ф), где юв = 2п/Т; Ав - амплитуда вынужденных колебаний. Изобразим нелинейность F[12] (рис. 4).

Нелинейность F [ 1 ₂ ] после гармонической линеаризации определится равенством

F [ 1 2 ] = F ⁰ [ А в , 1 2⁰ + 1 21 ] + q ( А в , 1 2⁰ + 1 21 ) 1 2» .    (3)

Коэффициент q ( А в , I 2 ⁺ I 21 ) = 0, так как нелинейность F [ 1 ₂ ] однозначна. Обозначим 1 20 + 1 ₂₁ = 1 ₂₀. Выражения для F ⁰ и q имеют вид, представленный на рис. 4 [ 3 ] :

F ⁰

K + K K - K

¹ , ² I 20 ⁺ —----^{2 х}

2           п где 12°, U0, у0 - постоянные составляющие; 121, U21,

Y ₁ - переменные составляющие, характеризующие автоколебательный режим; 1 ₂ » , U ₂ » - переменные, характеризующие вынужденные колебания в системе.

Метод решения. Так как частота автоколебаний много меньше частоты вынужденных колебаний, уравнение для определения вынужденных колебаний в системе принимает вид

Q ( p ) I 2* + R ( p ) ^F [ I 2 ] = R ( p ) ^F [ y ] ^cos ® в t , ⁽²⁾

х 1 ₂₀arcsin^ ° + А _в 1

k + к к q = —1---2 + —

-

K2L

п

I 20

А в ,

,

arcsin I ²⁰ + I ²⁰. 1

Г ²

I 20

.

где Q ( p ) = LCp ² + ( LY + Cr ) p + 1 + rY , R ( p ) = Cp + Y .

В уравнение (2) подставляем второе слагаемое из (3), где q определяется из второго уравнения (4). Параметры А _в и ф вынужденного автоколебательного режима определяются из равенств

A B = F [ Y ] ²

____Rj A²____

I Q ( j ^to B ) + q ( I 20 , A b ) R ( j ^to B )|²

ф П - arg ^[ Q ( j to B ) + R ( j to B ) q ( I 20 , A B ) ] + + arg [ R ( j ^to B ) ^] .

Выражения (5) определены с учетом

F [ y ] cos to _B t = F [ y ] sin I to _B t +^П j =

F M

AB

f n)

,    , sin ф— f   п)    Г 2 J.

cos ф| ф— I------- -t

I     ² j        ^to B

I 2* .

В результате решения (5) можно определить зависимость F ⁰( 1 ₂₀, A _в) от F[ y ], т. е. F 10 ( 1 ₂₀, F [ y ] ) , которая в дальнейшем используется для определения автоколебательного режима и решения уравнения для постоянных составляющих. Для этого F 1⁰ ( 1 ₂₀, F [ y ] ) представим в виде

F ( 1 20 , F [ y ] ) = Ф ⁰ ( 1 200 , F ⁰ [ Y ] ) + Ц 1 1 21 + Ц 2 A 1 , (6)

где 1 200 ,F ⁰ [ y ] - постоянные составляющие; A ₁ - ам-

плитуда первой гармоники вынужденных автоколеба-

d F ⁰

^ний; ^ц 1 =               , ^ц 2 =

^ ^{1 20} 1 200 , F 0 [ Y ]

d F 1⁰

.

^{д F} [ Y ] 1 00 , F 0 [ y ]

Нелинейность F [y] можно представить через коэффициенты гармонической линеаризации относительно автоколебаний в системе:

q y( ay ,Y0 ) = 4EsinnY0 J1 H ) • nay где J0 (nA), J1 (nA) - функции Бесселя первого рода соответственно нулевого и первого порядка.

C учетом (6) и (7) уравнение для определения параметров автоколебательного режима примет вид

N ( p ) + Ц 2 q y ( a y , Y ⁰ ) = ⁰,               ⁽⁹⁾

где

N ( p ) = E + kp [ 1 + Y ( p ₁ + r ) ] +

+ k [ LY + C ( p ₁ + r ) ] p ² + kLCp 3 .

Уравнение для постоянных составляющих:

Ey0 - Uon (1 + rY) - Ф0 [120, Ф0 (A,, Y0 )] = 0 .(10)

Из (9) определяются параметры автоколебательного режима:

2 = 1 + Y(^1 + r) to K = qy(ay,,») = -E-k[LY + COh + r)M .(11)

Ц 2

Следует отметить, что вместо Fy ( 1 ₂₀, F [ y ] ) , решая (5) и (10) совместно, можно определить нелинейную зависимость F ₂ ⁰ ( 1 ₂₀, , ) . Тогда, применив к ней разложение в ряд Тейлора и ограничившись первыми членами, можно найти

F 2⁰ ( 1 20 , y ) = Ф 02 ( 1 20 , Y ⁰ ) + П 1 1 21 + П 2 Y 1 ,         (12)

F [ y ] = Ф 0 ( A , Y 0 ) + q y ( a y , Y ⁰ ) Y i .          (7)

В (7) предполагается, что решение задачи определения автоколебательного режима в системе ищется в виде

Y = Y 0 + Y ₁ = Y 0 + A _Y sin to t .

Тогда

F 0 [ y ] = Ф 0 ( a y , Y ⁰ ) , A i = q y ( a y , Y 0 ) Y i ,

d F ⁰

где П1 = —   , d120 10,,0

d F 2⁰

.

d, ,0 _v0

I 2 , Y

В этом случае уравнения, аналогичные (10) и (11), примут вид

E y ⁰ - U оп ( 1 + rY ) - Ф 0 ( 1 0 , , ⁰ ) = 0,       (13)

₂   1 + Y (n + r)

^to K = —L H •         ⁽¹⁴⁾

П ₂ = E - k [ LY + C ( n ₁ + r ) ] to K .

где параметры автоколебательного режима определяются формулами

Ф 0 ( A Y , Y ⁰ ) = "2 П J 2E sin ( n ( y ⁰ + A Y sin v ) ) d V ,

1 2П 2E qy (ay , Y0) = -— J — sin(n (y0 + ay sin v)) sin VdV

Проведя интегрирование в (8), получим

-о/ .        2 E sinnY⁰_r \

Ф 0 ( a y , Y ⁰ ) = ^ J 0 ⁽ⁿ A ) .

Преобразованием (12) проведена обычая линеаризация нелинейности F [ , ]. Это можно делать только при значении , , близком к нулю или единице. Провести же аналитически гармоническую линеаризацию F\ ( 1 ₂₀, , ) затруднительно. Кроме того, как показывают исследования, характеристика F 0 ) ( 1 ₂₀, F [ y ] ) в широком диапазоне изменения 1 ₂₀ и F [ y ] близка к линейной. Так что погрешность от преобразования (6) гораздо меньше, чем (12). Но при малых и больших значениях , можно пользоваться уравнениями (12)–(14).

Нахождение граничных значений параметров фильтра, определяющих области устойчивости, производилось по уравнениям (11). Зависимости относительного значения постоянной времени выходного фильтра LC / T приведены на рис. 5 и 6, где Т – период частоты преобразования, от относительного изменения напряжения на источнике U ₁ U _1ном, где U 1 _но м = 1,5 ' U _1опт. Линии 1, отражающие границы устойчивости для режима непрерывных токов дросселя, определялись по линеаризованной системе уравнений (1), линии 2 по (11). Линии 3 отражают значения относительной постоянной времени фильтра, обеспечивающего заданный коэффициент пульсации.

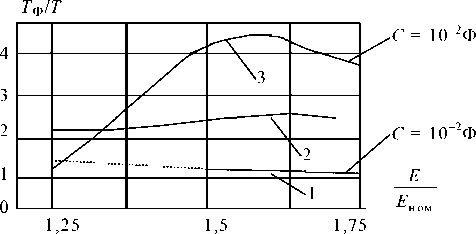
Рис. 5

Таким образом, графики показывают, что режим прерывистых токов дросселя фильтра расширяет область устойчивости. С возрастанием емкости выходного конденсатора и уменьшением сопротивления нагрузки увеличивается граничное значение постоянной времени фильтра. Однако даже при достаточно большом значении С и номинальной нагрузке затруднительно обеспечить низкий уровень пульсации выходного напряжения и одновременно добиться устойчивости стабилизатора при астатическом управлении.

T Ф / T

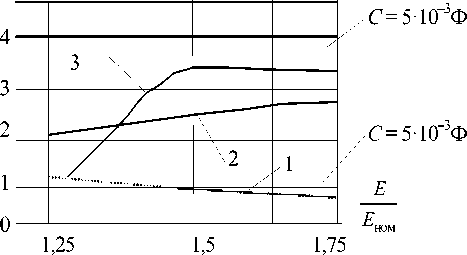
Рис. 6