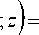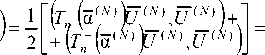Устойчивость теплицевых матриц и их положительная определенность

T n V^a    ; ^Z)

a 0 0 0 0 0 0 " 2a α0 0 0 0 L O 0 / 2a k 2α1 α0 0 0 L O 0 M 2a n-1 2αk 2α1 α0 0 L 0 0 M 2an-1 2αk 2α1 α0 O O • 0 L 0 0 2a n-1 2αk 2α1 «0 J n-1 t

= a о E n + 2 1 a k Z^k ( N x N )       (1)

k = 1

с элементным N -вектором

a^{( N} ) = Colona₀, 2a , , ^ 2a _k , ^ 2a _n _ 1 , 0, ^ 0 ] , (2) являющимся первым столбцом матрицы, поэтому мы можем записать:

a^{( N} ) = T n ( a^{( N} ) ; Z J^ ^N ) , ё/ ^N ) = Colon [ 1, 0, ^ 0 ] . (3)

Символом Zk (k = 0,1,...(n -1)) обозначим канонические матрицы сдвига размерности (N × N), введенные в [1; 2]. Это теплицевы матрицы вида (1) с элементными N-векторами в виде единичных векторов ek+? = Colon

0, L 0, 1, 0, L 0

123 k

( k = 0, n - 1) , ⁽⁴⁾

т. е.

k <

k          ( N )

^Z = T n l^a k + 1 ; ^Z ) =

0 L 0

1 O 0

01 0 L 0

0 L 0 1 0 L 0

( N x N ) ( k = 0, n - 1).         (5)

При k = 0 очевидным образом получаем единичную матрицу E_n = Z 0 .

Канонические матрицы (5) образуют линейно независимую систему теплицевых матриц, играющую роль базисных элементов в пространстве теплицевых матриц ( N × N ) вида (1), аналогично тому, как система единичных N -векторов (4) выполняет такую же роль в N -мерном векторном пространстве. Очевидно, полиномиальное представление в (1) есть разложение теплицевой матрицы по базису.

Введем l 1 -норму элементного N -вектора (2)

n - 1

I a^{( N} I = Ы+2 Z |a k l              ⁽⁶⁾

и максимальную столбцевую норму матрицы (1)

I ^T n ^{( a (} N ) ; ^Z J 1 = |a c|| E n I L + ² Z| a ktZ^k\ L =| ^⁽ N )|1 , ⁽⁷⁾

которая подчинена и согласована с векторной l 1 -нормой [3], а в нашем случае эти нормы будут просто совпадать, так как для столбцевой нормы канонических матриц имеют место равенства

I Z ^k | [ = 1 ( V k = 0,1,...) ( Z ⁰ = E n ) .

Заметим, что нормы (6) и (7) при n < N не зависят от N – порядка матриц.

Множество теплицевых матриц ( N × N ) вида (1) при всяких n ≤ N образуют линейное нормированное пространство. Но в нем определена и коммутативная операция умножения матриц, не выводящая за пределы указанного множества в силу свойств нильпотентности канонической матрицы Z ( N × N ):

Z ^k = 1 V k >  N ,            (8)

причем при всех m + n ≤ N – 1 для введенной матричной нормы выполняется кольцевое свойство:

I T , ( a ( ^N > ; ZT m ( » "'>; Z ) 1 < | T n (a' ^N > ; Z ) 1| T , ( » ^{, N} > ; Z J 1 =

= 1 ( ^{N ,}|J ^{b < N} )I1

Таким образом, указанное множество теплицевых матриц вида (1) образует коммутативную нормированную алгебру с единицей (нормированное кольцо) [1; 2]. Роль единицы, естественно, выполняет единичная матрица E N . Обозначим эту алгебру символом AT N ( Z ).

Всякой теплицевой матрице вида (1) может быть поставлен в однозначное соответствие порождающий полином n -1

P n ( a ⁽ N ⁾ ; Z ) = a 0 + 2 E a k Z (9) k = 1

комплексной переменной z с теми же вещественными коэффициентами, которые имеет матрица (1) в своем полиномиальным представлении по степеням матрицы Z ( N ×N ), т. е. в своем разложении по каноническому базису (5). Отметим, что именно это представление дало основание в [1; 2] назвать теплицеву матрицу (1) полиномиальной или просто P -матрицей. Эти термины, однако, мы использовать не будем.

Если полиномы вида (9) как функции комплексного переменного при всяком n ≤ N задать в единичной круговой области |z| < 1 комплексной плоскости z и снабдить переменную z свойством нильпотентности порядка N, т. е. считать, что zk = 1 Vk > N (10) (как уже отмечалось, это характерно для канонической матрицы Z (N × N)), то максимальное значение модуля комплексного полинома (9), которого он достигнет на границе единичной круговой области |z| = 1, причем и |zk | = 1 (k = 0, n —1), будет равно n1

“ ' z ) max = I”^{0 + 2 E} “ ^k =

=1 T- ^{li; )} ; ^Z 11,=1 H' N I=lI P n lI <^H> и совпадает с l ₁ -нормой элементного N -вектора (6) матрицы (1) и такой же ее нормой (7), поэтому может быть названо также нормой полинома (9).

Во множестве P N всевозможных полиномов вида (9), определенных в круге | z | < 1 и имеющих степени, не превышающие ( N – 1) ( n ≤ N ), содержится, очевидно, единица как полином нулевой степени и определены операции сложения и умножения на число, а также коммутативная операция умножения полиномов, которая, в силу условия нильпотентности (10) комплексной переменной z , также не выходит за пределы множества P N , причем для нормы произведения при всех m + n ≤ N – 1 выполняется условие

I Р . ^{( a}< N ^) ^p m b ™⁾ ; z )[ <| P , ^(a< N ⁾; z ) 1 pb™ Ц 1 =

= 1 l=

Указанные выше операции обладают всеми свойствами, необходимыми для определения множества PN как нормированной и коммутативной алгебры с единицей (нормированного кольца)

полиномов вида (9), заданных в круговой области |z| < 1 и имеющих степени, не превышающие величины (N – 1). Обозначим эту алгебру символом APN(z).

В силу однозначного соответствия n-1

Tn(a«0 + 2EakZk = k=1

= Pn (”

и равенства (11) для норм, алгебра ATN(Z) теплицевых матриц вида (1) становится изометрически изоморфной алгебре APN(z) соответствующих порождающих полиномов вида (9) [1; 2]. В частности, это означает, что всякие операции над матрицами – элементами алгебры ATN(Z) – одновременно осуществляются и над соответствующими порождающими полиномами – элементами алгебры APN(z), причем результаты этих операций как элементы своих алгебр сохраняют между собой прежние взаимно однозначные соответствия.

Вернемся к матрице (1). При любой ее конечной размерности и любом наборе {α_k } ее конечных элементов, причем a₀ * 0, эта n-диагональная теплицева матрица окажется невырожденной, так как

DetT_n (a<^N); Z) = aN * 0 VN > n.

При a₀ = 1 будем иметь матрицу вида (1), но с единичной главной диагональю

Tn^(,) (a^(N); Z ) = En + 2 Ea kZ^k (N х N) (N > n), ⁽¹³⁾ k=1

определитель которой равен единице при любых N, включая и предельный случай N ^ да . Матрицу (1) можно выразить через матрицу (13), рассматривая a₀ > 0 в качестве общего множителя всех других элементов:

Tn (a^(N); Z )= a 0

n-1        7

En + 2 E akZk k=1

= a0 ■ Tn⁽¹⁾(a^(N);Z) a\ = ”^ (k = 1,n — 1). (14) α₀

Очевидно, при любых a₀ > 0 свойства матриц (13) и (14) совпадают, но матрица (13) с единичной главной диагональю более удобна при рассмотрении этих свойств, поэтому далее вместо матрицы (1) будем использовать матрицу (13), опуская в обозначении все введенные верхние индексы, т. е. считая в (1) a₀ = 1 при прежнем обозначении:

Tn (a^(N);Z) = En + 2”E1akZ^k (Nх N) (N > n). (15) k=1

Этой теплицевой матрице будет соответствовать порождающий полином

Pn (a^(N); z )= 1 + 2 Ea kZ^{k            (16)}

k=1

с единичным свободным членом, заданным в единичной круговой области |z| < 1. При необходимости элемент а 0 * 1 может быть учтен путем умножения на него всех элементов матрицы (15) и коэффициентов соответствующего полинома (16). Очевидно, теплицевы матрицы вида (15) остаются элементами алгебры ATN(Z), а соответствующие им полиномы (16) – элементами алгебры APN(z), изометрически изоморфной алгебре ATN(Z).

Итак, будем работать с теплицевыми матрицами вида (15), т. е. с теми же матрицами вида (1), но при а0 = 1. Для таких матриц при любых N ≥ n существуют обратные матрицы (N×N) того же вида, но с N диагоналями:

т-1

T (а^(N);Z) = En + 2—рkZ^k (Nх N),    ⁽¹7)

к=1

и полновесными элементными N-векторами

Р^(N) = Coion[1,p1,...,eк,...,вN-1 ]=т-(а^(N);ZN^N) (18)

с l1-нормами

I в^(N )|L =| T-¹ (а^(N); z ]|, = 1 + —в к| = В к \ во = 1.⁽¹⁹⁾

^{11          111      11                          111}к=1 к=0

По выражению (18) следует, что элементный N-вектор β^(N) обратной матрицы (17) при любых N ≥ n, есть единственное решение уравнения

T_n (а^(N); Z)р^(N) = ё<^N).                (20)

Это, в частности, означает, что (n – 1) конечных элементов а_к (к = 1, n -1) исходной n-диагональной матрицы (15) определяют все (N - 1) элементов р_к (к = 1, n -1), р₀ = 1 обратной матрицы (17). При всяком конечном N и любом наборе конечных элементов а_к (к = 1, n -1) нормы (19) обратной матрицы (17) также являются конечной величиной. Однако при N ^ да сумма в (19) становится числовым рядом с положительными членами:

limТг-¹ (а^(N);Z)| = liml|р⁽N)|| = — в|, Ро = 1, (²¹)

N^да11 n Х ^1 NЛ      111   к=0' к| и для конечности l1-нормы матрицы (17) в этом случае уже требуется сходимость ряда в (21), что возможно лишь при определенных ограничениях на члены ряда, т. е. необходимы некоторые ограничения на элементы ак (к = 1, n -1) исходной матрицы (15), которые определяют все свойства элементов βk обратной матрицы (17) при любом N.

Таким образом, может быть выделен класс теплицевых матриц вида (15) (или вида (1) при а0 = 1), элементы которых ак (к = 1, n -1), кроме конечности обладают еще дополнительными свойствами, обеспечивающими конечность норм соответствующих обратных матриц при N ^ да .

Введем следующее определение. Одностороннюю n-диагональную теплицеву матрицу (15) назовем устойчивой, если l1-норма обратной ей матрицы (17) при N ^да окажется конечной величиной, т. е. если будет сходиться ряд (21).

Введенное понятие устойчивости односторонней теплицевой матрицы связано с использованием точечных моделей в теории линейных динамических систем [1; 2]. Дело в том, что векторноматричные равенства вида

T_n (а^(N); ZX^(N) = U^(N) о X^(N) = т;¹ (а^(N); Z)и^(N) (22) могут рассматриваться как точечные модели линейных динамических систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами и связывающих точечные изображающие N-векторы входного сигнала U^(N)и выходного X^(N)[1; 2].

Для l₁-нормы точечного изображающего N-вектора выхода имеем оценку

IX< N >1 < |T,-' (S<^N >; Z )| 1 U< «)|. (23)

Норма окажется конечной величиной при любых N, включая и предельный случай N ^ да , если такие же нормы входного N-вектора U^(N)и матрицы т,' (а^(N); Z) окажутся ограниченными при N ^ да, т. е. если теплицева матрица T_n (а^(N); Z) окажется устойчивой в смысле данного определения. Как установлено в [1], это означает устойчивость моделируемой динамической системы в обычном смысле, точнее в смысле «ограниченный вход – ограниченный выход».

Не вдаваясь в детали, отметим, что последнее связано с принципиально важным фактом: гомоморфизм алгебраических структур временных сигналов и их точечных представлений при N ^ да переходит в изометрический изоморфизм. При этом точечные модели динамических систем типа (22) становятся точными [1].

Введем еще одно понятие. Порождающий полином (16) односторонней n-диагональной тепли-цевой матрицы (15) будем называть также характеристическим полиномом этой матрицы, а алгебраическое уравнение степени (n – 1)

Pn (а(N); z )= 1 + 2—а kzk = 1 + 2а1 z + 2а 2 z2 +... + к=1

+ 2а_кz^k +... + 2а„ ,z^{n 1}= 0 к                    n 1

– ее характеристическим уравнением.

Уравнение (24) не зависит от размерности (N × N) матрицы и определяется ее элементами ак как коэффициентами, причем аn- 1 * 0. Число диагоналей матрицы (15), а это n ≤ N, определяет степень (n – 1) уравнения (24). А свойства характеристического полинома, естественно, определяют свойства соответствующей теплицевой матрицы.

Теорема 1. Для устойчивости односторонней n-диагональной теплицевой матрицы вида (15) необходимо и достаточно расположения всех корней ее характеристического уравнения (24) за пределами единичной круговой области, т. е. в области |z| > 1.

Доказательство. Оно может быть наиболее эффективно выполнено на основе фундаментального положения об изометрическом изоморфизме алгебры ATN(Z) теплицевых матриц вида (1) (или (15)) и алгебры AP_N(z) соответствующих порождающих (характеристических) полиномов. Как уже отмечалось, это означает однозначное соответствие всех алгебраических операций, осуществляемых над соответствующими элементами этих алгебр. Для операции обращения можем записать:

/ \ ( n-1 Л ¹( n-1 Л ¹

Гп-’^а(N⁾;Z)=|£n + 2Zа_AZk I ^Z^^ |1 + 2Zakzk | =

V k=1 ) V k =1 )

N-1

= Z в k |; в 0 = 1.

k=0

Очевидно, что в силу абсолютной сходимости ряда в (27) при |z| = 1 в предельном случае при N ^ да окажется lim Г-1 (a(N >; Z ) = liml Pу1 (a(N >; z ]| =

N ^«>11 n ^V111 N ^«H n ^V111

N-1         да

= ii^mZI^еt| =ZI^еt| <^да.          ⁽³⁰>

^N ^” k=0     k=0

= Pn

,-I

¹(a^(N)

W4^

n-1

1 + 2 Z a kZ k=1

Если характеристический (порождающий) полином

n-1

a⁽N⁾; z )= 1 + 2 Za kZ^k, k=1

По определению, это означает устойчивость матрицы T_n (a^(N>;Z). Теорема доказана.

Эта теорема содержит принципиально важное положение, касающееся размещения корней характеристического уравнения, гарантирующего устойчивость теплицевых матриц вида (1), но не дает какого-либо конструктивного алгоритма проверки выполнения этого требования. Однако на основе этой теоремы могут быть получены вполне конструктивные признаки устойчивости теплицевых матриц, не требующие определения корней характеристического уравнения. Некоторые из них будут рассмотрены ниже.

Вернемся к характеристическому полиному (26) теплицевой матрицы (15). Найдем его представление на единичной окружности |z| = 1 - граничной кривой круговой области |z| < 1, в которой определен полином. Положим z = e^п6 (-1 < 9 < 1) и отделим вещественную и

заданный в единичной круговой области |z| < 1, не имеет в ней нулей, т. е. уравнение (24) не имеет корней в этой области, то обратная функция Pn/ (a⁽N⁾; z) комплексного переменного z окажется аналитической в круговой области |z| < 1 и, следовательно, может быть представлена в ней степенным рядом Тейлора при z = 0:

мнимую части:

Pn (a^(N>; e'ⁿ⁹) = 1 + 2 Z a^e'k”⁹ = Pn (9) + Q)( (9),    ⁽³¹⁾

k=1

где

(32а)

‘ (328)

Pn (9) = Re| 1 + 2Z akeiⁿ⁹ ] = 1 + 2Z a_k cos kn9;

V     k=1         ) k=1

Q_n (9) = Imf 1 + 2 Z akeik⁶) = 2 Z a_k sin kn9.

V      k=1          ) k=1

/            \                1                        да

P.' (a⁽N⁾; z) =------1------= 1 + Ze^ z^k.

n                       n-1                     k

1 + 2 Z a _kz^{k      k}=1

k=1

Ряд сходится абсолютно для всех z из единичного круга |z| < 1, включая и его границу |z| = 1, поэтому для максимума модуля функции (27), принятого за его норму, при любых конечных N будем иметь

|| P^{- (a(}N⁾;^z | = max| PT^{1 (a(}N⁾;^z ] =¹+ Z|^ek |- ^{(28) 1} i^zi=1k=1

В силу изометрии алгебр, вместо соответствия (25) получим равенство для норм указанных элементов

I^т-(a(^N); Z ] 1 =|Pn-(^a< N >;^z ] 1 =

Вещественная часть P_n (θ) есть четный тригонометрический полином порядка n с такими же коэффициентами, какие имеет порождающий полином (26). Это означает, что тригонометрический полином (32а) способен характеризовать свойства как порождающего полинома (26), так и свойства соответствующей матрицы вида (15), в частности ее устойчивость в смысле данного ранее определения.

Теорема 2. Если четный тригонометрический полином (32а), как 2-периодическая функция окажется положительным, то теплицева матрица (15) будет устойчивой.

Доказательство. Согласно принципу аргумента теории функций комплексного переменного [4], при полном обороте вектора z = e^п9 вокруг начала координат плоскости z в положительном

направлении (против часовой стрелки) вектор (31), расположенный в комплексной плоскости (Pn, iQn), сделает столько полных оборотов вокруг начала координат этой плоскости, сколько нулей имеет полином (26) внутри единичного круга |z| < 1. Предположим, что при 6 = 0 (z = 1) тригонометрический полином (32а) как вещественная часть вектора (31) оказался положительным. Тогда мнимая часть (32б) как нечетная функция будет равна нулю и вектор (31) займет горизонтальное положение, совпадающее с положительным направлением оси Pn комплексной плоскости (Pn, iQn):

n-1

Pn (а^(N); 1)= Pn (0) = 1 + 2§ а к > 0.       ⁽³³⁾

к=1

Если при изменении переменной 6 от 0 до 2 тригонометрический полином (32а) сохранит свой положительный знак (вектор z = eiп6 при этом повернется на угол 2п, делая один оборот вокруг начала координат и перемещаясь своим концом по единичной окружности в положительном направлении), то это будет означать, что годограф вектора (31) останется в пределах правой полуплоскости комплексной плоскости (Pn, iQn) и не пересечет ее мнимой оси iQn, т. е. никакого вращения этого вектора вокруг начала координат происходить не будет. Согласно принципу аргумента, это означает отсутствие нулей у характеристического полинома (26) в единичной круговой области |z| < 1 и, следовательно, устойчивость теплицевой матрицы Tn (а(N);Z), согласно теореме 1. Теорема доказана.

Отметим еще один результат, устанавливающий связь между свойствами устойчивости и положительной определенности теплицевых матриц. Построим квадратичные формы

(т, (а^(N))и^(N\и^(N))= (и^(N\T⁺(а^(N))и^(N)) (34)

здесь для сокращения записи использовано обозначение Tn (а^(N))=Tn (а^(N);Z)

Будем  предполагать, что произвольный

N-вектор

U^(N) = Colon[U 1, l Uv, l Un]     (35)

при любых N > n имеет конечную 11-норму. Равенство (34) возникает в силу свойства скалярного произведения, которое порождает транспонированную верхнетреугольную теплицеву матрицу

Tn+ (а^(N); Z )= T, (а^(N); Z )= En + 2 § а к (z + ) к=1

(N х N) (N > n).           (36)

Равенство (34) позволяет представить квадратичную форму в виде

n

(а^(N) )u

(N) у (N)

= ( 1 [т, (а^(N))+ T_n⁺ (а^(N) )U^(N), U^(N) у

= (ST_n (а^(N))U^(N),U^(N))          (37)

где st, (а(N) )=2 [т, («(N))+Т+(а(N) )]= n-1

= En + § а к к=1

Z^k +

есть симметричная (2 n - 1)-диагональная тепли-цева матрица (N х N) (N > n) с единичной глав- ной диагональю.

Квадратичные формы в (37), построенные на указанных выше теплицевых матрицах, будут теплицевыми формами четного тригонометрического полинома (32а) [5], причем при всех N > n имеет место представление

(st, (а^(N) U^(N), u^(N)

)=(т, (а^(N) )U^(N)

и^(N)

NN

= §§ « к - тикит. к=1 т=1

Если квадратичные формы в (39) положительны при любых N-мерных векторах (35) с конечными 11-нормами, то они называются положительно определенными. Это понятие распространяется и на теплицевы матрицы, на которых строятся указанные квадратичные формы.

Известен следующий результат [5; 6].

Утверждение 1. Для положительного четного тригонометрического полинома n-1

P_n (6) = 1 + 2 § а_к cos кпб         (40)

к=1

необходимо и достаточно положительной определенности теплицевых форм (39), т. е. выполнения условия

(т, (а^(N) )U^(N), U^(N)) = (ST, (а^(N) )u^(N), U^(N)) > 0 (41)

для всех N > n.

Обратное утверждение также верно: положительность полинома (40) с необходимостью означает выполнения условия (41).

Это утверждение и теорема 2 позволяют сформулировать следующий результат.

Теорема 3. Для устойчивости односторонней n-диагональной теплицевой матрицы (15) необходимо и достаточно выполнения условия (41), т. е. положительной определенности при всех N > n самой матрицы (15) и, что равносильно, симметричной теплицевой (2n - 1)-диагональной матрицы (38).

Доказательство. Если выполняются условия теоремы 3, которые, согласно утверждению 1, одновременно являются необходимыми и достаточными условиями положительности полинома (40), то, в силу теоремы 2, односторонняя тепли-цева матрица (15) окажется устойчивой.

Следствие. Если односторонняя n-диагональная теплицева матрица (15) устойчива, то при всех N > n будет устойчивой и обратная ей матрица t/U(N);z)=En + 2ЕвiZ (n*n).       (42)

k =1

Рассмотрим векторно-матричное уравнение с невырожденной теплицевой матрицей (15) и произвольным N-вектором U^(N)в правой части:

Tn (a^(N);Z)x^(N) = U^(N).          (43)

Умножим скалярно обе стороны этого уравнения на N-вектор X^(N):

(Tn (a^(N);Z)x^(N\X^(N))= (u^(N),X^(N))

Если выполняется условие

Tn (a^(N);Z)x^(N),X^(N))=

= (U(N), X(N) )> 0 (VN > n),(44)

то, согласно теореме 3, матрица T_n (a^(N); Z) будет устойчивой. Единственное решение уравнения (43)

X(N) = T"1 (a(N); Z )U (N)

умножим скалярно на N-вектор U^(N):

(X^(N), U^(N) )= (u^(N), X^(N) )= (t^-1 (a^(N); Z )u^(N), U^(N))

В силу (44) окажется

(N) x(N))=(т-1(а( N)z\u(-N) u(N)Ko U , X ) Tn v" ; / U ,U/ > 0

(VN > n),(46)

что означает положительную определенность матрицы (42) и, следовательно, ее устойчивость, согласно теореме 3.

Замечание. Утверждение следствия непосредственно вытекает и по факту однозначного соответствия алгебраических операций, осуществляемых над элементами изоморфных алгебр ATN(Z) и APN(z), т. е. над теплицевыми матрицами вида (15) и их порождающими (характеристическими) полиномами. Это фундаментальное положение было использовано при доказательстве теоремы 1.

Для операции обращения односторонней теп-лицевой матрицы T_n (a^(N); Z) будем иметь следующее представление для характеристических полиномов:

р;^г (a^(N);z)=----n^^-----= 1 + NIP_kz, (VN > n)..

1 + 21 akz     ^k=1

k=1

Оно возможно, если полином

P_n (a^(N);z)= 1 + 211a_kZ не будет иметь нулей внут-k=1

ри единичной круговой области |z| < 1, т. е. если соответствующая матрица Tn (a^(N); Z) устойчива.

Формально имеет место и равенство обратных сумм

1                   n-1

—N----= 1 + 21 akz, (VN > n),

1+IPkz      k=1

k=1

которое также возможно лишь при условии отсутствия нулей внутри единичного круга |z| < 1 у полинома р^-1(a^(N); z) при всех N > n, что означает устойчивость обратной матрицы Tn^-1(a^(N); Z).

Итак, свойство устойчивости односторонних теплицевых матриц вида (1) (или (15)), в смысле данного ранее определения, эквивалентно свойству положительной определенности как самих этих матриц, так и их симметричных двойников (38), что сводится к требованию положительности соответствующих квадратичных (теплицевых) форм при всех N > n, т. е. к условию

(т_п (a^(N))U^(N),U^(N))=(ST_n (a^(N))u^(N),U^(N))>0. (47)

Непосредственная проверка этого условия означала бы либо определение всех (вещественных) собственных значений симметричной матрицы STn (a^(N)) при различных N > n, которые все должны быть положительными, либо проверку по критерию Сильвестра. И то, и другое в общем случае оказывается задачей аналитически неразрешимой. Это означает крайнюю неконструктивность условия (47). Значительно более конструктивным является утверждение теоремы 2, согласно которому устойчивость матрицы (15) и, следовательно, ее положительная определенность гарантируется положительностью тригонометрического полинома (32а), т. е. выполнением условия

P_n (6) = 1 + 2 "fa _k cos kn0 > 0 б (-1 < 6 < 1), (48) k=1

что возможно при определенных ограничениях на коэффициенты полинома. Такие ограничения определяют так называемые достаточные признаки положительности. Рассмотрим один такой признак.

Теорема 4. Если l1-норма односторонней n-диагональной теплицевой матрицы (15) удовлетворяет условию

I Tn (a^(N); Z )| = 1 + 2 f| a Д< 2, ^{(49) 11 111}k=1

то четный тригонометрический полином (32а) окажется положительным за период, а матрица устойчивой.

Доказательство. Попытаемся найти те ограничения, которые нужно наложить на элементы α_k симметричной теплицевой матрицы (38), чтобы все ее вещественные собственные значения оказались положительными, что означало бы положительную определенность матрицы, положительность тригонометрического полинома (32а) и, следовательно, устойчивость матрицы (15).

Все круги Гершгорина для симметричной теп-лицевой матрицы (38) сливаются в один круг n-1

I^ -1| < 2 z a a=r              (50)

k=1

с центром на вещественной оси комплексной плоскости z в точке z = 1 и радиусом n-1

2 Z| a k| = R.                     ⁽⁵¹)

k =1

Круг (50) отсекает на вещественной оси отрезок [1 – R, 1 + R], в котором и располагаются все вещественные собственные значения симметричной теплицевой матрицы STn (a(N)). Других собственных значений матрица не имеет. Очевидно, указанный отрезок будет целиком располагаться на положительной половине вещественной оси и все собственные значения матрицы окажутся положительными, если будет выполняться условие n -1

1 - R > 0 о R = 2Z|a_k| < 1,             (52)

k=1

что эквивалентно условию (49) для l1-нормы матрицы (15). Теорема доказана.

Отметим, что условие (52) определяет множество положительно определенных матриц вида (38) со строгим диагональным преобразованием. Условие (49) или (52) легко проверяемо для любой теплицевой матрицы вида (15), но является довольно жестким ограничением, поскольку оно выделяет узкий класс устойчивых теплицевых матриц.