Устойчивость тонкостенного холодногнутого профиля при изгибе - краткий обзор публикаций

Construction of Unique Buildings and Structures journal homepage:

В последние годы в России на фоне динамично развивающейся металлургии и растущего спроса на металлическую продукцию особое внимание уделяется легким стальным тонкостенным конструкциям (ЛСТК).

Тонкостенные конструкции в сравнении с традиционными горячекатаными металлическими конструкциями имеют ряд технологических и эксплуатационных достоинств (малый удельный вес конструкций, экономичность, приспособленность для изготовления на потоковых автоматизированных линиях и т.д.) [9].

Благодаря этим достоинствам ЛСТК находят широкое применение в различных областях промышленного и гражданского строительства [9, 65, 53].

Тонкостенные конструкции хорошо зарекомендовали себя при строительстве малоэтажных жилых и гражданских, а также универсальных производственных зданий [130, 132] (рисунок 1). Не менее широко ЛСТК применяются в составе традиционных строительных систем для устройства покрытий и надстройки мансардных этажей существующих и новых строений [131].

Рисунок 1. Каркас производственного здания из ЛСТК

В последнее время ЛСТК начали активно применяться в конструкции ограждающих панелей в сборно-монолитном строительстве [9, 25, 133]. Такие панели получили название термопанелей (рисунок 2а).

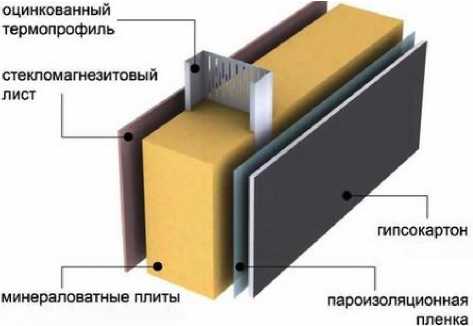
Рисунок 2. а – принципиальная схема устройства термопанели, б – схема движения теплового потока в термопрофиле

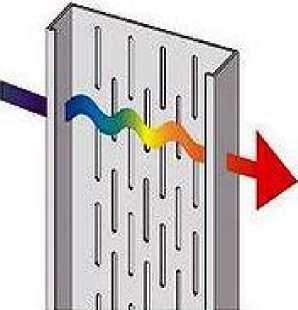
Для уменьшения теплопотерь в подобных панелях в качестве несущих элементов применяются профили с просечками, так называемые термопрофили. Благодарю наличию просечек в панелях не образуется «мостик холода», что приводит к повышению эффективности самой панели (рисунок 2б).

Однако, такое преимущество тонкостенных конструкций, как легкость, при определенных условиях оборачивается недостатком, существенно уменьшающим их несущую способность [53, 29, 134]. Отрицательной особенностью тонкостенных конструкций является склонность к потере устойчивости при 33

Гарифуллин М. Р., Ватин Н.И. Устойчивость тонкостенного холодногнутого профиля при изгибе — краткий обзор публикаций. / Garifullin M.R., Vatin N.I. Buckling analysis of thin-walled cold-formed beams — short review. © нагрузках заметно ниже проектных, что затрудняет их проектирование и, как следствие, ограничивает их широкое применение.

Как показывает практика, зачастую из-за ошибок в проектировании зданий из ЛСТК, нередки аварийные случаи. Так, например, в ночь с 24 на 25 декабря 2010 г. в Брянской области произошло обрушение сельскохозяйственного здания. Как выяснилось позже, сооружение было изначально неверно запроектировано, в результате чего верхний пояс, соединенный на болтах жестко со стойками, потерял устойчивость и стал причиной аварии (рисунок 3).

Рисунок 3. Потеря устойчивости верхнего пояса фермы из ЛСТК

Таким образом, обеспечение устойчивой работы таких конструкций является важнейшей задачей на пути широкого внедрения ЛСТК в массовое строительство. Очевидно, тонкостенные конструкции уже на стадии проектирования требуют тщательного анализа их несущей способности и, особенно, касаемо вопросов устойчивости.

Несмотря на растущую популярность подобных конструкций и большой объем научных исследований на всем этапе развития ЛСТК, на сегодняшний день в России имеются существенные недостатки в нормативной, методической и расчетно-вычислительной базах проектирования ЛСТК, которые не позволяют легко и однозначно производить их расчет.

Во введенном в 2011 г. своде правил [42] содержатся указания по проверке общей устойчивости изгибаемых элементов сплошного сечения без дифференциации конструкций на тонкостенные и толстостенные. Свод правил уделяет большое внимание вопросам проверки устойчивости стенок и поясных листов изгибаемых элементов, расстановке ребер жесткости, однако не рассматривает наиболее важный случай, когда ребра жесткости не предусмотрены по конструктивным соображениям. Устойчивость формы поперечного сечения не рассмотрена вовсе. Также не затрагиваются вопросы взаимодействия различных форм потери устойчивости.

Руководство по проектированию стальных тонкостенных балок [43] содержит указания по прочностному расчету тонкостенных стержней с учетом редуцирования поперечного сечения, однако, при этом, совершенно не рассматривает проверку их устойчивости.

Рекомендации Айрумяна Э. Л. [33] хоть и содержат более четкие указания по расчету прочности тонкостенных элементов, дифференцируют расчет устойчивости тонкостенных элементов в зависимости от типа сечения, но, несмотря на это, в вопросах проверки местной устойчивости во многом ссылаются на действующий СНиП II-23-81 «Стальные конструкции».

Подобное состояние дел приводит к неясности и отсутствию единогласия среди проектировщиков во многих вопросах проектирования ЛСТК и, как следствие, стимулирует формирование научной базы по расчету подобных конструкций для создания четких методик их расчета.

Основная задача данной статьи — провести краткий обзор отечественных и зарубежных публикаций по рассматриваемой теме, выявить основные тенденции развития расчетных методик и определить наиболее перспективные и актуальные направления дальнейших исследований.

Обзор отечественных работ

Основы развития методов расчета тонкостенных стержней на протяжении XX и начала XXI вв. подробно описываются в работе Рыбакова В.А. [53].

На сегодняшний день все существующие методы расчета тонкостенных конструкций принято условно подразделять на две основные группы: основанные на стержневом моделировании и на оболочечном [26, 53].

К первой группе относятся аналитические методы, предусматривающие моделирование стержня с учетом такого силового фактора, как бимомент [17-19, 36]. Основной проблемой таких методов является их сложность и трудоемкость, трудность их программирования и, как следствие, необходимость ограничиваться лишь рамками теоретических исследований.

В основе второй группы расчетов лежит представление тонкостенного элемента в виде оболочки и дальнейший расчет с применением численных методов, наиболее распространенным из которых является метод конечных элементов [1-8, 21-23, 26-28, 31, 32]. Важной особенностью этой группы расчетов является широкое использование для расчета программных комплексов (SCAD, MicroFE, SOFiSTiK, ANSYS и проч.), существенно уменьшающих трудоемкость вычислений и позволяющих успешно решать широкий спектр задач различного уровня. Такие способы расчета позволяют получить достаточно точные для инженерных расчетов результаты, однако являются весьма трудоемкими при проектировании многостержневых конструкций.

Большой вклад в развитие теории тонкостенных элементов внес А. Р. Туснин, в работах которого [6, 45, 46] предлагается метод тонкостенных конечных элементов (ТКЭ). В ТКЭ в каждом узле кроме учитываемых при расчете обычных стержневых систем трех линейных и трех угловых степеней свободы учитывается седьмая степень свободы узла – депланация сечения. Таким образом, ТКЭ с узлами в начале и конце имеет 14 степеней свободы.

Туснин А.Р. и Туснина О.А. [128] представили вычислительную систему «Сталькон» для расчета стальных стержневых конструкций с учетом нормативных требований.

Туснин А.Р. и Прокич М. [129] приводят теоретическое обоснование коэффициента, учитывающего развитие пластических деформаций, для балок двутаврового сечения при действии бимомента, а также предлагают методику для расчета двутавров на стесненное кручение.

Перельмутер А.В. и Сливкер А.И. в книге [10] предлагают способ моделирования тонкостенных элементов при помощи так называемой «бистержневой модели», что позволяет выполнять расчет тонкостенного стержня, оставаясь в рамках ограничений стандартного программного обеспечения, оперирующего конечными элементами с твердотельными узлами.

Каменских И.В. [62] предлагает для расчета устойчивости тонкостенных конструкций использовать метод модуль-элементов, снижающий размер системы уравнений равновесия в 10-100 раз по сравнению с методом конечных элементов. Доказывается приемлемость дискретизации конструкции на пространственные модуль-элементы, даны рекомендации по разбиению конструкций на модуль элементы.

Рыбаков В.А. [63] предлагает метод расчета тонкостенных конструкций на основе полусдвиговой теории Сливкера (2005), учитывающий часть деформаций сдвига в срединной поверхности стенок стержней, вызванных действием секториальных сил.

Лалиным В.В. [26, 27] рассмотрено построение матриц жесткости тонкостенных конечных элементов различных типов по полусдвиговой теории Сливкера и по бессдвиговой теории расчета Власова в зависимости от способа аппроксимации функций деформаций, рассмотрены задачи о стесненном кручении тонкостенного стержня, имеющего различные граничные условия на концах с точки зрения сходимости и поиска статических силовых факторов.

Большой вклад в исследование проблем устойчивости тонкостенных конструкций внес Белый Г.И. [17-19]. В работе [17] он приводит приближенный аналитически-численный метод деформационного расчета упругопластических тонкостенных стержней двусимметричного сечения, что предполагает использование частных решений задач недеформационного расчета и бифуркационного расчета устойчивости.

В работе Белого А.Г. [20] в общем виде решена задача деформационного расчета и устойчивости для стержней произвольного профиля (открытого, замкнутого и комбинированного) при действии продольной силы, приложенной с двухосным эксцентриситетом.

В работах Воронцова Г.В. [58, 59] предложены варианты линеаризованных дифференциальных уравнений «геометрически» и «физически» нелинейных задач об изгибно-крутильных деформациях тонкостенных стержней открытого профиля. Рассмотрены два «шаговых» метода решения исходной нелинейной задачи. Получены общие выражения для формирования последовательно уточняемых матриц жесткости стержней как систем с 14-ю степенями свободы с возможностью внедрения их в программы метода конечных элементов при расчете стержневых нелинейно деформируемых конструкций [60].

Богданович А.У. [50-52] исследует работу стержней переменного сечения, для которых использование известных уравнений Власова-Тимошенко не представляется возможным. Приводятся уравнения и методики расчетов, позволяющие решать задачу прочности и устойчивости тонкостенных стержней непрерывно-переменного сечения с учетом возможного появления пластических деформаций и геометрической нелинейности процесса деформирования стержня.

В работе Юрченко В.В. [36] предложены аналитические зависимости для определения значений критических сил при расчете устойчивости центрально сжатых тонкостенных стержней С-образного профиля. Рассматриваются случаи потери устойчивости элементов поперечного сечения (местной потери устойчивости), а также потери устойчивости формы поперечного сечения тонкостенного стержня.

Евзеров И.Д. [30], рассматривая некоторые задачи устойчивости для стержней и пластин, получил представления перемещений по сечению стержня и толщине пластины для геометрически нелинейных задач, выполнил переход от вариационной постановки трехмерной задачи устойчивости к соответствующим задачам для стержней и пластин.

Методика расчета центрально и внецентренно сжатых неидеальных стержней прямоугольного профиля в критическом и закритическом состояниях изложена в работах Ильяшенко А.В. [54-56], в которых в качестве расчетного метода использован принцип возможных перемещений.

Группой ученых из ННГАСУ [11] изложены результаты исследований несущей способности тонкостенных стальных конструкций с учетом развития пластических деформаций и конструктивных факторов в неразрезных ригелях и большепролетных рамных конструкциях переменного сечения.

Юзиков В.П. и Завьялова О.Б. [41] для расчета тонкостенных стержней открытого профиля предложили методику учета сдвига срединной поверхности, получили дифференциальные уравнения изгиба и кручения, а также матрицу жесткости.

Синельщиков А. В., Юзиков В. П. [40] предлагают математическую модель тонкостенного стержневого конечного элемента с прямолинейной осью и переменным сечением.

В работе Беловa И.Д. и Юрченко В.В. [39] освещен вопрос нормативного проверочного расчета устойчивости тонкостенных холодногнутых профилей открытого сечения в соответствии с российскими и украинскими строительными нормами, уделено внимание определению редуцированных размеров поперечных сечений элементов из тонкостенных холодногнутых профилей для тех случаев, когда гибкость элементов сечения превышает их предельное значение.

Анализ пространственной устойчивости элементов рам и колонн переменного сечения при действии продольной силы и изгибающего момента проведен в работе С. И. Билыка [38]. Получена система дифференциальных уравнений работы упругого стержня с переменным сечением в плоскости действия момента. Предложено приблизительное решение системы дифференциальных уравнений при аппроксимации момента инерции сечения и секториального момента инерции сечения параболической зависимостью. Разработана методика проверки устойчивости упругой двутавровой колонны переменного сечения из плоскости действия изгибающего момента.

В работе Хайруллина Ф.С. [64] разработаны вариационные методы определения напряженно-деформированного состояния тонкостенных конструкций, основанных на использовании функций с конечными носителями произвольной степени аппроксимации.

Сурьянинов Н.Г. [61] для расчета тонкостенных стержней обобщил метод граничных элементов, построил математические модели тонкостенных стержневых систем открытого, замкнутого и комбинированного профиля при статических нагрузках, определил фундаментальные решения описывающих их дифференциальных уравнений.

Астахов И.В. [13-15] разработал алгоритм и программу расчета на пространственную устойчивость тонкостенных стержневых элементов из гнутых профилей открытого сечения с учетом различных условий загружения; фактического распределения механических характеристик стали и остаточных напряжений; начальных искривлений и углов закручивания; формы сечения; а также возможной потери местной устойчивости.

Особый интерес и большую практическую ценность подставляют работы по численному анализу устойчивости тонкостенных конструкций с применением программно-вычислительных комплексов, в основе большинства из которых лежит метод конечных элементов. Компьютерное моделирование позволяет в сжатые сроки проводить исследования большого количества образцов с учетом начальных несовершенств, различных условий закрепления, а также анализировать все виды потери устойчивости, включая местную. На фоне целого ряда публикаций по этой теме особо выделяются работы ученых на базе СПбГПУ [1-5, 8, 9, 16, 25, 28], проводящих масштабные исследования перфорированных тонкостенных конструкций — термопрофилей, широко применяемых в производстве ограждающих панелей.

В работе Ватина Н.И. и Поповой Е.Н. [9] приводится история развития производства и становления тонкостенных конструкций в России, освещаются основные области их применения, проводится общий анализ напряженно-деформированного состояния, а также даются рекомендации по компьютерному моделированию термопрофилей.

Синельников А.С. и Орлова А.В. [1] приводят результаты экспериментальных и аналитических исследований прочности и устойчивости холодногнутого просечно-растяжного профиля.

Смазнов Д.Н. [3, 4] рассматривает устойчивость и формы потери устойчивости холодногнутых стоек из высокопрочной стали, дает рекомендации по оптимальным шагам разбиения элементов, приводит практические рекомендации для конструирования новых типов поперечных сечений с рациональным расположением жестких вставок [5].

Ватин Н.И., Рыбаков В.А. [16] проводят сравнительный анализ ручного и автоматизированного расчета тонкостенной консольной балки швеллерового сечения и делают вывод о применимости действующих на тот момент строительных норм к проектированию подобных сооружений.

Рыбаков В.А. и Гамаюнова О.С. [25] провели исследование прочностных и жесткостных характеристик термопрофиля, предложили способ его моделирования с учетом просечек, а также установили их влияние на его жесткостные характеристики.

Недвига П.Н. и Рыбаков В.А. [28] предложили методику испытаний прочности стальных холодногнутых тонкостенных балок с отсутствием и наличием продольных просечек, определили зависимости прочности балок от конструктивных и технологических параметров.

В статье Гордеевой А.О. [8] разработана подробная методика построения конечно-элементных расчетных моделей перфорированных профилей в SCAD.

Задачи устойчивости центрально сжатых перфорированных стоек рассмотрены в работах Шатова Д.С. [2], Назмеевой Т.В.[29].

Юрченко В.В. [7] проводит анализ напряженно-деформированного состояния каркаса здания из тонкостенных холодногнутых профилей при помощи SCAD с использованием трехмерной конечноэлементной модели.

В статье Кретинина А.Н. и Крылова И.И. [12] произведен анализ напряженно-деформированного состояния тонкостенной балки из гнутых оцинкованных профилей в упругой стадии работы материала, проведено сравнение теоретических и экспериментальных результатов.

Теплых А.В. [21] приводит результаты линейных и нелинейных статических расчетов устойчивости стенок двутавровых балок и рам с использованием расчетных комплексов SCAD и Nastran, приводит рекомендации по выбору типа расчета и соответствующих коэффициентов в зависимости от гибкости элементов.

Кикоть А.А. [22] рассматривает задачу о влиянии ширины поясов и отгибов в сечениях C- и Z-образных стальных тонкостенных холодногнутых профилей на эффективность работы в условиях изгиба и отмечает, что характер влияния ширины поясов на эффективность во многом зависит от толщины стали. В работе [23] автор разрабатывает алгоритм и компьютерную программу определения прогибов изгибаемых элементов из стальных тонкостенных холодногнутых профилей с учетом потери местной устойчивости и потери устойчивости формы сечения, показывает области предпочтительного применения программы.

В статье Ветюкова Ю.М. и Елисеева В.В. [24] рассмотрен пример решения задачи об изгибно-крутильной потере устойчивости прямого стержня при сжатии в сравнении с классическим решением Эйлера, существующими решениями для существующих стрежней и численным решением в оболочечной постановке.

В публикации Марченко Т.В. и Банникова Д.О. [34] выполнен сопоставительный анализ форм потери устойчивости стержневых тонкостенных элементов открытого профиля. В частности, проведены расчеты по определению критической силы центрально сжатых тонкостенных стержней по аналитическим и численным методикам расчета, а также по действующим нормативным документам.

В статье Лещенко А.П. [35] описан расчет устойчивости внецентренно сжатого двутаврового стержня методом аналогии и сравнение с результатами эксперимента при различном эксцентриситете.

В работе Волковой В.Е., Макаровой А.А. [37] выполнено конечноэлементное исследование напряженно-деформированного состояния балки с гибкой стенкой конвейерной галереи с учетом геометрической нелинейности. Рассмотрена проблема снижения локальных напряжений и обеспечения местной устойчивости стенки балки.

Ольков Я.И., Полтораднев А.С. [48] провели численное исследование работы тонкостенной двутавровой балки с гибкой стенкой с учетом геометрической и физической нелинейности.

Теоретические и экспериментальные исследования устойчивости стенки тонкостенного профиля несимметричного сечения проведены в работе Зверева В.В. и Мещеряковой Е.В. [44].

Максак В. И. и Максак Т. В. [47] проводят расчет основного обрешеточного тонкостенного составного неравнобокого двутаврового кронштейна открытого профиля на вертикальную нагрузку и подтверждают результаты расчета экспериментом.

Потапов А. В. [49] предлагает метод расчета на устойчивость стальных стержней открытого профиля с различными типами поперечных сечений при их работе за пределом упругости. В реализации метода учитывается возможность потери устойчивости, как в стадии упругого деформирования, так и в стадии неупругого деформирования, то есть с учетом развития пластических деформаций.

Чернов С.А. [57] рассматривает устойчивость при центральном сжатии тонкостенного стержня открытого профиля с недеформируемым контуром поперечного сечения, производит сравнение результатов аналитического расчета на устойчивость тонкостенного стержня и расчета методом конечных элементов по разработанной программе для ЭВМ.

В работе [127] авторы проводят анализ работы пространственной металлической конструкции покрытия большепролетного спортивного сооружения, а также выполняют поиск наиболее рациональной геометрической схемы главной несущей конструкции.

Вопросы устойчивости тонкостенных трапециевидных профилей при продольно-поперечном изгибе подробно рассмотрены в работах Холкина Е.Г. [66-68].

Обзор зарубежных публикаций

Широкое применение ЛСТК находят и за рубежом [65, 126]. Проблеме устойчивости тонкостенных холодногнутых конструкций посвящено множество работ, исследований, публикаций.

Стоит отметить следующее: в иностранных публикациях авторы выделяют 3 основные формы потери устойчивости: местная (local buckling), устойчивость формы поперечного сечения (distortional buckling) и общая (global buckling): изгибная (flexural) и/или крутильная (torsional). В некоторых статьях исследуются вопросы их взаимодействия [34, 35, 89, 90, 103].

В настоящее время, все методы расчета тонкостенных конструкций, как правило, делятся на две основные группы: аналитические и численные. Некоторые из этих методов кратко представлены в этой статье.

Метод приведенной ширины (Effective Width Method)

В настоящее время, метод приведенной ширины (МПШ) является одним из традиционных методов расчета тонкостенных конструкций. Основанный Т. фон Карманом в 1932 г., доработанный Г. Винтером МПШ превратился в основной метод расчета тонкостенных конструкций, реализованный в спецификации AISI – строительных нормах Северной Америки. Тем не менее, в связи с эмпирическим происхождением МПШ имеет приблизительные коэффициенты редуцирования и неочевидную природу используемых уравнений, что, в свою очередь, ограничивает его широкое применение.

Ю Ч. и Ян В. [69] предлагают метод расчета, основанный на МПШ для расчета устойчивости формы сечениянаиболее распространенных холодногнутых С и Z секций, работающих на изгиб.

Ли Л. и Чен Дж. [108] представили аналитическую модель для анализа устойчивости формы сечения холодногнутых Z и Σ профилей.

Чу К. и Кеттл Р. [109] представили аналитическую модель для расчета изгибно-крутильной формы потери устойчивости тонкостенных швеллеровых балок, частично раскрепленных в поперечном направлении листовым металлом, при воздействии подъемных нагрузок.

Унгуреану В. [111] создал базу данных для геометрических и аналитических моделей расчета несущей способности некоторых наиболее часто используемых холодногнутых профилей.

Виейра Дж. [113] предложил и верифицировал упрощенные модели для расчета продольных усилий, возникающих в С-образных тонкостенных прогонах.

Роджерс К. и Шустер Р. [117] исследовали поперечные деформации сопряжения полок и стенок сечений тонкостенных элементов, сравнили аналитические методы расчета на изгиб с существующими результатами экспериментальных исследований.

Трахаир Н. и Хэнкок Г. [118] разработали упрощенный метод расчета устойчивости тонкостенных элементов из плоскости действия момента, в котором редуцированный модуль упругости используется для моделирования влияния остаточных напряжений и начальных несовершенств.

Ли Л. [124] представил аналитическую модель для предварительного расчета изгибно-крутильной формы потери устойчивости холодногнутых Z-образных прогонов, частичного раскрепленных из плоскости листовым металлом.

Обобщенная теория балок (Generalized Beam Theory)

Обобщенная теория балок (ОТБ) была первоначально разработана Шардтом Р. [70] и доработана Дэвисом Дж. и коллегами [71]. ОТБ позволяет эффективно прогнозировать различные формы потери устойчивости тонкостенных конструкций, и, что главное, исследовать их взаимодействие.

Сильвестр Н. и Камотим Д. [72] применили ОТБ для исследования изгиба стальных холодногнутых конструкций. В [73, 74] они представили аналитическую формулу на основе ОТБ для оценки бифуркационных напряжений холодногнутых колонн, балок и балок-колонн с произвольно наклоненными продольными ребрами жесткости.

Абамбре М. [75] использовал подход на основе ОТБ для исследования геометрически и/или физически нелинейной работы призматических тонкостенных стержней, испытывающих произвольные деформации и сделанных из нелинейных изотропных материалов.

Базалья К. [76] представил результаты ОТБ-исследований устойчивости холодногнутых стальных С и Z прогонов, раскрепленных листовой сталью.

Бебиано Р. с коллегами [77] представили GBTUL 1.0β – бесплатную программу, позволяющую рассчитывать холодногнутые элементы на устойчивость и динамические нагрузки. Программа, разработанная на кафедре строительства и архитектуры Технического университета Лиссабона, является численной реализацией ОТБ.

Гонсалвес Р. [110] представил формулировку ОТБ для выполнения анализа потери устойчивости тонкостенных стержней с произвольными поперечными сечениями.

Базалья К. [123] представил результаты численного исследования на основе ОТБ различных форм потери устойчивости холодногнутых стальных прогонов, раскрепленных из плоскости момента и подверженных действию подъемной нагрузки.

Луо Х. [125] представил две вычислительные модели на основе ОТБ, позволяющих анализировать несущую способность холодногнутых тонкостенных швеллеров, изгибающихся в плоскости наибольшей жесткости.

Нейронные сети (Neural Networks) и Генетическое программирование (Genetic Programming)

Нейронные сети (НС) успешно используются в решении сложных проблем в различных областях техники. Адели Х. впервые применил НС для проектирования зданий и сооружений. Ташакори А. и Адели Х. [78] использовали НС для оптимизации холодногнутых стальных пространственных конструкций. Эль-Кассас Е. с коллегами [79] использовали НС для расчета критической нагрузки для холодногнутых стальных профилей.

Пала М. в [80] рассмотрел применение НС для расчета критической силы при потере устойчивости стальных тонкостенных элементов. В [81] он предлагает новую формулу на основе НС для исследования устойчивости формы поперечного сечения стальных холодногнутых шарнирно-закрепленных швеллеров.

В [82] Пала М. исследует упругую устойчивость формы поперечного сечения стальных холодногнутых элементов помощью генетического программирования.

Метод конечных элементов (Finite Element Method)

Метод конечных элементов (МКЭ) – один из наиболее распространенных численных методов, используемых для исследования тонкостенных конструкций. На сегодняшний день существует множество вычислительные комплексов на основе МКЭ, которые позволяют успешно анализировать работу холодногнутых элементов.

Шафер Ч. Ю и Шафер Б. в работах [83, 84] описывают серию экспериментов по исследованию местной устойчивости [83] и устойчивости формы поперечного сечения [84] холодногнутых стержней при работе на изгиб. В статьях приводится сравнение различных методов расчета с прямым прочностным методом. Статья [85], будучи логическим продолжением статей [83, 84], верифицирует используемые конечноэлементные модели и выполняет параметрические исследования, выходя за рамки описываемых экспериментов.

В статье [86] представлен КЭ анализ устойчивости холодногнутых стальных элементов с круглыми отверстиями, усиленными ребрами жесткости.

Жао И. с коллегами [87] описывают упрощенные методы расчета устойчивости формы поперечного сечения стальных тонкостенных конструкций.

Гарднер Л. и Незеркот Д. [88] представляют последовательный подход к численному моделированию работы стержней круглого замкнутого сечения из нержавеющей стали, подвергнутых различным видам нагрузок.

Расмуссен К. [89, 90] приводит экспериментальные результаты и последующее подробное КЭ моделирование взаимодействия различных форм потери устойчивости тонкостенных балок из нержавеющей стали.

Хайдарали М. и Незеркот Д. [91] рассматривают два вида конечноэлементных моделей для исследования устойчивости раскрепленных из плоскости тонкостенных холодногнутых балок с учетом свойств материала и геометрических нелинейностей.

В работе [92] Хайдарали М. и Незеркот Д. исследуют влияние краевых ребер жесткости на работу сжатых полок сечений. В статье [93] они оценивают влияние размера и расположения промежуточных ребер жесткости на процесс потери устойчивости поперечно раскрепленных холодногнутых стальных балок.

Пастор М. и Рур Ф. [104, 105] приводят результаты экспериментальных и численных исследований тонкостенных U- и Ω- образных элементов, подвергнутых чистому изгибу.

Айдин М. [112] проводит КЭ анализ изгибной и изгибно-крутильной форм потери устойчивости элементов тонкостенных рамных конструкций.

Моэн К. и Шафер Б. [114] разработали и обобщили упрощенные методы аппроксимации общей иместной форм потери устойчивости, а также устойчивости формы поперечного сечения перфорированных холодногнутых колонн и балок.

Ренс В. коллегами [115] представляют точные конечно-элементные модели для прогнозирования работы и критической силы тонкостенных стальных швеллеров, подвергнутых чистому изгибу.

Саманта А. и Кумар А. в работе [116] рассматривают устойчивость формы поперечного сечения моносимметричных двутавровых балок в зависимости от характера приложения нагрузки.

Пачош П. и Василевич П. [121] представляют результаты экспериментальных исследований тонкостенных балок двутаврового сечения, сравнивают значения критической нагрузки с результатами, полученными аналитически и с помощью метода конечных элементов.

Магнушки К. [122] описывает теоретические решения проблемы устойчивости холодногнутых тонкостенных балок открытого и закрытого профиля и подтверждают результаты экспериментально.

Метод конечных полос (Finite Stripe Method) и прямой прочностной метод (Direct Strength Method)

Метод конечных полос (МКП) – эффективный, легко программируемый метод для анализа тонкостенных конструкций. В настоящее время МКП получил широкое распространение благодаря целому ряду преимуществ по сравнению с МКЭ.

Большой вклад в развитие применения МКП для расчета тонкостенных конструкций внес Шафер Б. . На основе МКП он разработал прямой прочностной метод (ППМ) [94], который был принят американским институтом стали и сплавов (AISI) в 2003-2004 годах в качестве альтернативного метода расчета холодногнутых конструкций.

В статье [97] Шафер Б. сравнивает три новые оценочные методики, основанные на ППМ, с расчетными методами в американских нормативных документах; отмечает ограничения ППМ.

Адани С. и Шафер Б. [119, 120] приводят теоретическое обоснование и практические примеры для модального разложения форм потери устойчивости тонкостенных элементов, ограничивая традиционные решения МКП.

Шафер Б. и Адани С. [95] приводят техническое обоснование и примеры анализа устойчивости холодногнутых стальных элементов с использованием ими же разработанной программы CUFSM, в основе которой лежит МКП.

Шафер Б. и Пекоч Т. [96] рассматривают МКП-моделирование холодногнутых стальных элементов, уделяя особое внимание вопросам геометрических несовершенств и остаточных напряжений.

Эккер Г. [98, 99] применил изопараметрический метод конечных полос (ИМКП) к анализу перфорированных тонкостенных стальных конструкций.

Яо З. и Расмуссен К. [100, 101] представили аналитические разработки и численную реализацию ИМКП к физически и геометрически нелинейному анализу перфорированных тонкостенных стальных конструкций.

Зиракян Т. в исследовании [106] проводит анализ потери устойчивости формы поперечного сечения симметричных двутавровых балок с гибкой стенкой.

Чу К. с коллегами [107] описывают исследование местной устойчивости и устойчивости формы поперечного сечения стальных холодногнутых швеллеровых балок при воздействии на них равномерно распределенной нагрузки.

Метод приведенных площадей (Effective Area Method) и Метод приведенных сечений (Effective Section Method)

Метод приведенных площадей (МПП) является прямым методом, первоначально разработанным Батистой М. для расчета тонкостенных колонн [102]. Основанный на компьютерных разработках метода конечных полос МПП в настоящее время используется для исследования взаимодействия местной и общей форм потери устойчивости холодногнутых стальных элементов. Метод приведенных сечений (МПС), являющийся продолжением МПП, недавно был включен в строительные нормы Бразилии в качестве метода расчета стальных холодногнутых элементов.

Батиста М. [103] проводит анализ прочности стальных холодногнутых балок и колонн с использованием МПС, сравнивает его с традиционный методом приведенной ширины.

Заключение

Подводя итоги проведенного обзора работ, можно сделать следующие выводы:

• 1.    На сегодняшний день тема исследований тонкостенных холодногнутых конструкций является актуальной и перспективной — это подтверждается огромным количеством публикаций результатов теоретических и экспериментальных исследований ЛСТК, как российских, так и иностранных.

• 2.    Как видно из анализа зарубежных работ и публикаций, на сегодняшний день большинство стран в мире имеют собственные, устоявшиеся, четко сформулированные и проверенные многочисленными экспериментальными исследованиями нормативные базы для расчета тонкостенных конструкций (система еврокодов в Европе, спецификация AISI в Северной Америке и др.). Тем не менее, налицо активное развитие и внедрение других, более прогрессивных и точных расчетных методов, как например Direct Strength Method в Америке, Effective Section Method в Бразилии, Generalized Beam Theory и проч. Кроме того, большое внимание уделяется исследованиям местной устойчивости и устойчивости формы сечения, множество публикаций посвящено проблемам начальных несовершенств и различных условий закрепления. Освещены вопросы взаимодействия различных форм потери устойчивости.

• 3.    В России отсутствует единый нормативный документ, позволяющий проектировщикам просто и однозначно рассчитывать соединения из тонкостенных конструкций, что порождает большой интерес к данной теме. Однако, несмотря на целый ряд теоретических исследований, в настоящее время не сформулирован и не реализован практический подход к решению данной задачи. Очень мало публикаций экспериментальных исследований работы тонкостенных конструкций на сжатие и, особенно, на изгиб, практически отсутствуют публикации по исследованию местной устойчивости и устойчивости формы сечения. Все это, на фоне активного развития компьютерных технологий, подталкивает проектировщиков и исследователей все чаще прибегать к помощи мощных вычислительных комплексов на основе МКЭ для моделирования работы тонкостенных конструкций. Стоит отметить целый ряд подобных работ, в которых авторы добились достаточной для инженерной практики совпадения теоретических и практических результатов. Однако, среди проектировщиков нет единого мнения в вопросах применимости таких методов, нет четких рекомендаций по шагу разбиения сетки и вопросам закрепления, остается открытым вопрос моделирования и учета действия просечек термопрофиля и, самое главное, не определены коэффициенты запаса. Все это, с учетом большой трудоемкости процесса компьютерного моделирования, создает определенные трудности для инженеров. И все же, положительная тенденция полученных результатов на фоне растущего интереса к тонкостенным конструкциям оставляет надежду, что в скором времени отечественные инженеры увидят столь долгожданный и желанный нормативный документ, который позволит без проблем рассчитывать тонкостенные конструкции и откроет им дорогу на отечественный рынок.