Устойчивость трехслойной панели со свободным краем в составе конструкции космического аппарата

При проектировании трехслойных пластин, применяемых в конструкциях космических аппаратов, часто возникает задача расчета устойчивости пластины, когда один из ее краев свободен.

Задача устойчивости такой пластины наиболее подробно изучена для случая, когда к шарнирно закрепленным краям приложена равномерная сжимающая нагрузка.

Вместе с тем большой практический интерес представляет случай, когда к шарнирно закрепленным краям пластины приложены линейно изменяющиеся усилия.

Уравнения устойчивости такой пластины содержат переменный коэффициент, и поэтому их интегрирование оказывается затруднительным. В данной статье решена задача определения критических усилий для трехслойной пластины со свободным краем под действием линейно-изменяющейся нагрузки.

Рассмотрим трехслойную пластину с одинаковыми композитными несущими слоями и ортотропным заполнителем. Два противоположных края пластины шарнирно-оперты, а один край жестко закреплен.

Пластина нагружена в своей плоскости линейно-изменяющимся усилием.

Запишем выражения для потенциальной энергии деформации трехслойной пластины [1]:

ba

1 bar

U = 2 II D

, ^;dO ^v ' - _n 50.50 y

>3— - + 2 D ₁₇—- —- + 11                   12

V d x )        d x d y

Согласно методу Канторовича, представим прогиб и углы поворота в следующем виде w - wm (y) sin x 0   0„; (y) cos x mmxxm  m

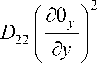
⁺ D 33

00 " I

V d y   5 x )

⁰ y ^-0 ym ( у ) sin ^ m ^x ^ m =П т ( m ^- 1, ², ³, 3   ⁽⁷⁾

I CW 1              CW

+ к I 0 +— I + kv 0 +— xx     yy

V     d x )      V     d y )

и для работы внешних сил:

ba

ba

A = 2 II N X

о 0

dxdy

d w I 2

d x

+ 2 N w a w + N y (a w V y 5 x d y     ^y V d y )

При рассматриваемом нагружении

dxdy (2)

N 0 - — N I 1 - 2 - I ,    N y - 0, N 0 = 0.      (3)

V b )

Вариация энергии деформированной пластины

ab Г(

⁵ U - II I

0 0 LV

n 50x n 50y 3(50xI D11 a + D12 a           l + dx       dy ) V dx )

(  50     503 (503

+ D„ —x + D ₇₇ — 5     + D₃₃

12           22                        33

V     e x       d y ) V d y )

(50. 50 y 3(503

I —-+—- ISI —- l +

V c y   5 x ) V d y )

50. 50y 3(50y I    (d

+5 ---- + Kx 0y +--50 у + xxx dy   dx Mdx ) Vd

5 w

d y

d x

+ K 0 + — xx

50 - +

^{+ K} y

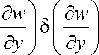
dxdy .

и вариация работы внешних сил

ba

1 Г Г I        V W CW 1 i CW 1

5 A - — f I N [ 1 - 2 y H— I5I — I dxdy (5)

2 00 V     b IVd x ) Vd x )

Таким образом, получим основное вариационное уравнение деформированной трехслойной пластины

ab Г(

II [ D i

00 LV

d0 x       ⁶⁰ у Ы^е x I (_ d0 x  _ 5⁰ y I

+ Di ?--- 5 --- + D --+ D??

12                          1222

dx       dy ) V dx ) V    dxd

( (50 y I _n (50. 50 y 3(50j _n (50. 50 y I x5I l + D ₃₃ I x +I5I x I + D ₃₃ I x +lx

V c y ) V d y d x ) V d y ) V d y d x )

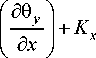
, dw 3л x + 150 x + Kx dx )

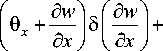
I      5w i           I      5w i I 5w

+ K y |0 y +—|50 y + K y |0 y +^-|5l^-

V     d y )          V     d y ) V d y

Подставим (7) в (6) и выполним необходимые преобразования. Тогда получим

0 L

xm

- 0v„

D i2З, — ym 50.„ +

12 m          xm dy )

ы (1 y^y I( ^{d w} W^{5 w} I

— N I 1 — 2— II   I5I ---- I

V     b ) V d x ) V d x )

dxdy - 0 .        (6)

Получим решение уравнения (6) с помощью метода

Канторовича и обобщенного метода Галеркина [2; 3].

^{(     d 0} ym

⁺ I D 22   ,

V dy

I ( d 0 I

D l ₂3,⁰xm 5 — ym + 12 mxm

) V dy )

1 rx    u 0xm 1            c  M0xm.

+ D33 -----+ 3,0,,,„ 5  +

V dy ) V dy )

+ D 33R m- " Tm +^ m 0 ym I50 ym + V -у )

+ K_X (0xm +31 w„ )50_xm + K_x (30xm +3 w „ )5 w „ + xxmmm xm xmxmmm m

+ K y |0 ym + dw m I50 ym + K y |0 ym V dy ) V

dw m 3( dw m

+         I5I

dy

dy

X ²m N ( 1 — 2 - I w m 5 w m d- - 0. V b )

Далее выполним операцию варьирования функционала в уравнении (8), и получим три вариационных уравнения с естественными граничными условиями

b

f k (30,„+3 w„ xmxm mm

^{- 0} ym ₊ ^{d 2 w} m dy dy ²

b

^ m N ( 1 — 2 - I w V b )

b

I

⁵ w m dy ⁺ K y I ⁰ ym

dw „ 3

+ M I5wm dy)    J0

- 0,

b Г                      (

I ^K x ⁽⁰ xm ⁺ ^ m w m ^{) +} I D 11 ^ m ⁰ xm

0 L                       V

d 0

D 12 ^ m-Tm dy

n [ ^{d 0 xm}

D 33     2

dy ²

d 0

m dy

50, „dy + xm

b

+

y

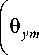
m

D 33 \-f + + ^ m 0 ym I 50 xm

. V dy            )      J 0

dw m ^I dy )

(

D 22

- 2 0 ym dy ²

+ D 33 3 m-^ + 3 0 ym I V dy )

„  ^{- 0} ym

D ₂₂ dy

- 0,

^— D 12 ^ m

- 0x1,1I xm dy

50 ym -У +

b

D l ₂31⁰хт 50

mxm ym

⁾         -I 0

- 0.

+

Решим систему вариационных уравнений (9) обобщенным методом Галеркина. В соответствии с этим, представим прогиб и углы поворота в следующем виде

w m = A m U y ( У ) , ⁶ xm = B m ^U y ( У ) , ⁶ ym = C m V y ( У ) ,

здесь A_m , B_m , C_m – неизвестные числа, подлежащие определению; U_y ( y ) , V , ( y ) - известные функции,

аппроксимирующие прогиб и углы поворотов. функции имеют вид

Г, ,3      „2                           >1

Эти

b

b

b

U , dy = 0

b

A m K x X m J U y² dy + B_m K x J U , d, + D _nX m J U , dy

V 0

U y ( y ) =

y

4 - 4 4 + 6 ^y - 12 y b b ³     b ²     ь

, - 2 b

,

v (, )=y[    - y yW 613 62 6

Kyb ^{2 где Y} У =-р-D 22

.

Вариации функций (11) будут wm = Uy8Am , 6xm = Uy8Bm , 6,m

= V , 8 C m .

Подставив (10) в (9), с учетом (12), получим

J K x ( X m B m U y +X² m A m U y )

^{- K} ,

f    dV,

y m dy

d ² U dy ²

A

X m N [ 1 - 2 , | A m U y U y 8 A m dy +

V 6 7

dU 1

C m V y + A m-Л I U y 8 A m dy 7

= 0,

J 0

b

0 _

I    , 7                   dV

+ | D 11 X m B m U y - D 12 X m C m-A

V                       d,

b

^{- D} 33

f d2 Uv        dVv yy

Bm . 7 ^+X mCm ₇

dy ²           dy

U y 8 B m dy +

[     dUv             1

D 33 I B m-A + X m C m V y I U y 8 ^B.

V     dy           7

= 0,

m

^] 0

[       d ²V_v           dU 1

- D 22 C m”Г - ^D12^X m B m-p +

dy

dy

L     dU_V „

>33 I X m B m-p + X m C m V ,

V        dy

V y 8 C m dy +

dV               1

D22 '   . — ^X mBmUy I Vy 8 Cm dy                7

= 0,

J 0

Учитывая произвольность вариаций 8 A m , 5 B_m

и

8 C m получим систему разрешающих уравнений обобщенного метода Галеркина в следующем виде

b

b

A m K x X m J U y dy - K y J U y

d 2 U dy ²

dU_v dy + K, Uy—^ dy

J 0

b

b

V 0

dV y dy

-

+

0 b

d ² U y

—— dy + D 33

f       6    dV..             6dV..

D 12 X m J U y -ydy + D 33 X m J U y -Cdy -

V      0    dy           0

b

- D 33 J U y

c

m

dU

U y^y dy

^{] 0} 7

^D 33 ^X m UV , ] 0 ) = 0,

^b dU

A m K y V y-T dy + B m 0 dy

(

V

b

dU dy

^b dU                   b

+ ^D„C m J Vy^d, - ^D 13 ^l m [U,^V, ] 0

[ + C m

b

b

D 33 X m J V y² dy - D 22 J V y

V

b

г 7           dV

+ K y J V y² d, + D 22 V y-C dy

+

d ² V y

-"TT d у ⁺ dy

b

= 0.

^{] 0} 7

Введем обозначения входящих в уравнения интегралов и безынтегральных членов

b

1 1 У = J ^U;d, ;

b    d 2 U

• ¹ 2    у = J U y -r/ d, ;

₀ dy ²

^b    dV_y

• ¹ 3    У = J ^Uy , ⁽d^{; ;}

₀ dy

b

b

^J , У = J V' ; d, ;

b

^J 2 У = J V y-p d, ;

b

J3 У = J Vy

₀ dy

1 1 y = 01 - 2 У I U , dy ;

0 ^{V 6 7}

R 1

1 y

; R 2 y =

dU

U y^y dy

b

■ ; R 3 , =

J 0

dV ^y V y dy

b

.

J 0

Численные значения ных членов (15) будут

8 b

^{1 y} 315 ^{Y 1 y} ;

J ^{2 y}     5 6 ’

J ³ у = 365 ^Y 3 у ;

где

интегралов и

безынтеграль-

b

J 1 y 14

; I _{2 y}

I = ^Y3 У - ^{3 y} 35 ;

= - 35 6 ^{72 y} ’

T = ^Y3 у -

^{3 y} 35 ;

2 b

1 1 У =--Yi V ;

^{1 y}     315 ^{1 y}

R i y = Y i y ;

R 2 y = 6 ^Y 1 У ;    R 3 У = ⁰ ,

Y iy = 91 + 999 y y + 3024 y , ;

Y 2 y =— 5 + 28 y y + 560 y , ;

Y 1 y = 220 + 2043 y y + 4536 y 2 ;

Y 1 y = ^{1 +} 4 Y y ; Y 3 y = ^{5 +} 14 Y у ; Y 3 y = ^{5 + 56} Y y . ⁽¹⁷⁾

Принимая во внимание, что А 1 _y — 1 _{3 y} = J 3 _y , и подставляя (16) в (14), получим систему линейных алгебраических уравнений относительно неизвестных чисел A_m , B_m и C_m

. ,8 b 12            12-     .

KCm---Ylv+ Kv ---Y2v + Kv --Y1 v A + i x m 315 иy y 35b /2y y b иy i m

+ K Cm---Y1 Bm + Ki Y3 Cm -^m N---Y1 Am = 0, xm315 1ym   y35 3ymm315 1ym

8 b      Л      lb 8 b     , П у 2 8 b

KCm ---Y1 Am + K---Y1 v + D\ Cm ---Y1 v + x m 315 1       ( x 315 1 y    11 m 315 1 y

~ 12        12A

+ D33 AaY2У + D33 TY1У IBm + 35bb

+ 1 D3 Cm — A- D Ст™ I C„ = 0,(18)

33 m 35 3 y 12 m 35 m

6 7 4 .In. у 6                     ^Y3 У In .

Kv   Ya v^m + D^ V^m   Y3v D A^mB^m y35 3ym33 m35 3y12 m35 m

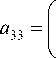
a 31 = ^a 13 ;      a 32 = a 23 ;

45Y y      6345

^ 2 22 2 n

2 n m r n m r 2

Величина n, входящая в уравнение (19) и опреде- ляемая равенством

Nb ²

n= ,

D 11 D 22

называется безразмерным коэффициентом устойчивости трехслойной пластины.

Однородная система (19) будет иметь нетривиальное решение только тогда, когда будет выполнено условие det(A) = 0 .                     (23)

Решив уравнение (23), получим аналитическое выражение параметра n, которое после упрощения с учетом равенств (28) примет следующий вид

= a 11 a 22 a 33 ^{+ 2 a} 12 ^a 12 a 23 ^— a 11 a 23 ^— a 22 ^a 13 ^— a 33 ^a 12

П                                      (                  2 \                             . \ / b11 ( a33a22 — a23 )

+ 1 K_v— + D ₂₂ — + D₃₃— X 2 I C_m = 0. ( ^y 14     ²² 5 b ³³14 ^m J ^m

Приведем систему (18) к удобному для вычислений безразмерному виду. Для этого умножим обе час-315 b ти каждого уравнения на величину             ,

2X m V D n D 22

и, обозначив F_xm = aB_m и F_xm = bC_m , получим дующее матричное уравнение

AF = O

сле-

где

I an

A = ^

П b n

a ₁₂

a ₁₃

Величина n зависит от числа полуволн деформации m вдоль оси ординат. Точке бифуркации формы равновесия пластины, очевидно, соответствует такое m , при котором n принимает минимальное значение. Это значение и будет соответствовать критическому коэффициенту устойчивости пластины п _кр .

При известном значении п _кр , из равенства (22) определим критическое усилие для трехслойной пластины

DD

N кр =П кр ^±Jb_r^^L. I²⁵)

a ₂₁

a ₂₂

a ₂₃

;

a ₃₁

a ₃₂

a 33

I A m

F =

\F

I ym

;

O = < 0

.

Элементы матрицы A имеют вид

a_n =

4 Y 1 y Y x r ⁺

54 Y 2 У Y У ¹⁸⁹⁰ Y 1 у Y,

22 n m r

22 n m r

;

^b 11 = ^Y 1 y ;   a 12 =

4Y1 yYxr nm ’

a

_ 27 Y 3 y Y y ,

13 =    2 2

n m r

;

a 22 =

4 Y 1 y Y x r

2 2~ n m

a 21 = a 12 ;

⁺ 4 Y 1 y

⁵4 Y 2 y r ₃₃ 18⁹⁰ Y ₁ y r ₃₃

-2 2 n m

-2 2 n m

;

a 23 =

27 Y 3 y r 33   9 Y 3 y r 12

n m

2 n m

;

В качестве примера расчета, определим критическое усилие для трехслойной пластины, с рассматриваемым закреплением краев. Суммарная толщина несущих слоев пластины принимает значения t = 0.001, 0.002 м; толщина слоя заполнителя h = 0.01, 0.05, 0.1 м.

Материал несущих слоев характеризуется модулями Юнга E x = E y = 54.55 ГПа, модулями сдвига G_xy = 20.67 ГПа, G_xz = G_yz = 3.78 ГПа, и коэффициентами Пуассона ν_xy = 0.32, ν_yx = 0.32. Материал заполнителя характеризуется только модулями сдвига G xz = 440 МПа, G xz = 220 МПа. Размеры пластины в плане: a = 0.5; 1; 1.5; 2; 3; 5 м; b = 1 м. Результаты расчетов для пластины представлены в табл. 1.

Верификация результатов расчета критического усилия выполнена в конечно-элементном пакете COSMOS/M с помощью конечного элемента SHELL4L [4] (табл. 2). Сравнение результатов обоих расчетов позволяет сделать вывод о достаточной точности предлагаемого метода, так как расхождение результатов не превышает 5 %.

Таблица 1

Критические усилия для трехслойной пластины

Параметр			a , м; ( b= 1 м)
			0.5	1	1.5	2	3	5
h, м; ( t = 0.001 м)	0.01	ηкр	75.402	28.766	22.358	22.846	22.358	22.086
		N кр , кН/м	114.08	43.524	33.828	34.566	33.828	33.416
		m	1	1	1	1	2	3
	0.05	ηкр	71.962	28.616	22.441	22.963	22.441	22.189
		N кр , кН/м	2577.8	1025.1	803.88	822.61	803.88	794.86
		m	1	1	1	1	2	3
	0.1	ηкр	67.838	28.347	22.474	23.045	22.474	22.250
		N кр , кН/м	9909.6	4140.8	3283.0	3366.4	3283.0	3250.2
		m	1	1	1	1	2	3

Таблица 2

Критические усилия для трехслойной пластины, вычисленные МКЭ

Параметр			a , м; ( b= 1 м)
			0.5	1	1.5	2	3	5
h , м; ( t = 0.001 м)	0.01	N кр , кН/м	111.13	42.611	33.342	34.169	33.394	33.047
		m	1	1	1	1	2	3
	0.05	N кр , кН/м	2493.7	996.57	786.76	807.61	787.88	780.53
		m	1	1	1	1	2	3
	0.1	N кр , кН/м	9621.2	3997.8	3190.6	3281.4	3195.3	3169.2
		m	1	1	1	1	2	3

Таким образом, решена задача определения критических усилий трехслойной пластины со свободным краем, у которой два противоположных края шарнир-но-закреплены, а один край жестко закреплен. Для решения уравнений устойчивости был использован метод Канторовича и обобщенный метод Галеркина. Выполнена верификация полученного аналитического решения, показавшая, что определение критических усилий может быть выполнено с достаточной инженерной точностью без значительных вычислительных затрат. Поэтому полученные формулы могут быть полезными при проектировании трехслойных пластин.