Устойчивость за пределом упругости

Generalization of the formula of Euler on not elastic area and definition of critical force in the compression member behind a limit of elasticity is considered in article. It is set an example of calculation in which comparison of the decisions received by methods of F.Engessera, T.Karmana and I.Tsurkova which involves laws deformation theories of plasticity is resulted.

Ultimate stress which was determined on resulting module, gives superior limit of stress for load capacity of a design, on tangent module – limiting minimum, stress, on module Tsurkova it located between these solutions.

Устойчивость систем или боковое выпучивание сжатых элементов имеет большое практическое значение. Это особенно справедливо во многих новейших конструкциях, где размеры поперечного сечения делаются все меньшими и меньшими благодаря использованию прочных материалов и в целях экономии веса. Развитие методов исследования и формирование представлений о работе стержневых систем при развитых пластических деформациях, когда существенно изменяется их жесткость, является одной из актуальных проблем механики деформируемого твердого тела. Решение этой научнотехнической проблемы имеет важное народно-хозяйственное значение.

Целью настоящей работы является определение критического напряжения в сжатом стержне, материал которого не следует закону Гука.

Разрушение стержня может произойти из-за потери устойчивости, т.е. стержень не сохранит той формы, которая ему придана конструктором; при этом изменится и характер напряженного состояния в стержне.

Определение критической силы в сжатом стержне долгое время привлекает внимание крупных ученых многих стран мира, таких как Л. Эйлера, Е Ламарля, И. Баушингера, Л. Тетмайера и М.

Консидера, Ф. Ясинского, Т. Кармана, С. Тимошенко, Ф. Шенли, В. Власова, Е. Попова, Н. Корноухова, А. Ильюшина, Ю. Работнова, И. Цуркова и др. [1-19].

Для стержней из линейного упругого материала критическая сила была определена Л. Эйлером (1744г.). Он составил уравнение устойчивости: приравнял изгибающей момент, который соответствует бесконечно малому искривлению упругой оси стержня моменту внутренних сил

π ² nEJ _min ^кр      ( µ l )^{2    ;}

где E - модуль упругости, J - минимальный момент инерции, µ - коэффициент приведения длины стержня l , λ - гибкость стержня, n – произвольное целое число.

Критическое напряжение равно:

σ _кр

π ² E

λ ²

Если потеря устойчивости стержня происходит за пределом упругости, то нормальные напряжения, как в зоне догрузки, так и в зоне разгрузки, будут пропорциональны не модулю упругости, а секущему модулю, который сам зависит нелинейным образом от продольной деформации в рассматриваемой точке, в соответствии с диаграммой «напряжение-деформации». При исследовании устойчивости сжатого стержня в неупругой области надо привлекать законы деформационной теории пластичности. Однако известные исследования в этом направлении не учитывают этого обстоятельства.

Ф.Энгессер (1899г.) при выводе формулы для критической силы за пределом упругости предположил, что напряжения в любой точке сечения определяются по закону Гука, но при этом обычный модуль упругости он заменил, на так называемый касательный модуль.

_π 2 _E σ кр =     ₂ ^k ,

Δσ где E = tgα =    - касательный модуль.

k      k   _{Δ ε}

Так как в решении Ф. Энгессера зоны догрузки и разгрузки не различаются, то Т. Карман для уточнения решения, предложил двухмодульную модель поперечного сечения: в зоне догрузки имеет место касательный модуль, а в зоне разгрузки остается обычный модуль упругости. Решение Т. Кармана, как и решение Ф. Энгессера, не обосновано, вследствие того, что каждую из зон они считают линейно упругой.

π ² T

P_кр =      ₂

где T =

4 E k E

( E k + E )²

T

- результирующий модуль , λ = π     .

^σ кр

Критическое напряжение в данном случае:

_π 2 _T

σ _кр =    ₂

На рисунке 1 построена диаграмма «напряжение-удлинение» для дуралюмина Д 16Т. Основной модуль упругости принят равным          ⁴     , предел пропорциональности          ²      .

пц

Для определения касательного модуля, в различных точках диаграмм (a, b, c, d и т.д.) проводим касательные и находим их тангенсы углов наклона к оси абсцисс.

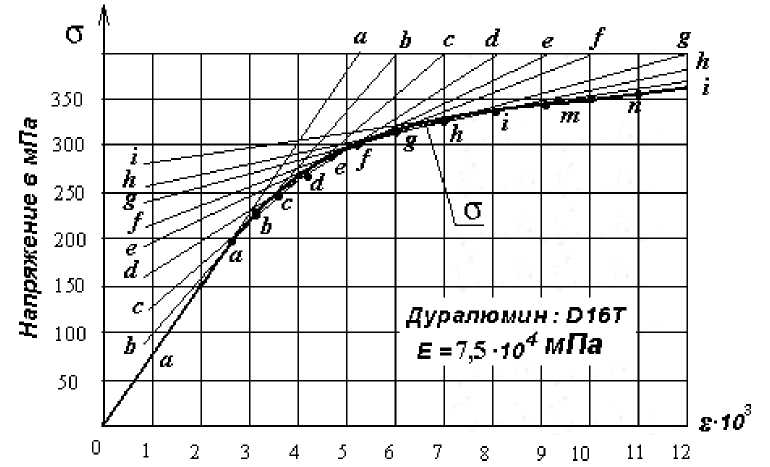
Рисунок 1. Диаграмма «напряжение-удлинение»

Величины E , соответствующие ряду значений напряжения σ и относительной деформации сжатия ε , приведено в таблице. Здесь же приведены вычисленные по формуле (5) значения величины результирующего модуля T и гибкости λ ; они относятся к двутавровому сечению, для примера основного случая сжатого стержня с шарнирно-закрепленными концами.

Полученная зависимость между гибкостью стержня двутаврового сечения и критическим напряжением выражена графически на рисунке 2.

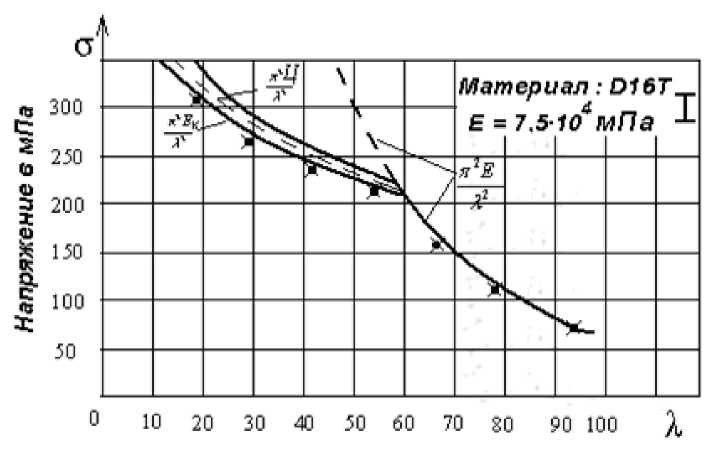
Рисунок 2. Зависимость критического напряжения от гибкости

Для упругой области, при λ ≥ 60 , кривая построена по формуле Эйлера [1]. При тщательной постановке опытов, с точным соблюдением всех предпосылок теории, экспериментально получаются критические напряжения, лежащие достаточно близко к кривой, построенной по формуле (5). Однако, опыты показали, что в большинстве случаев формула (5) с «результирующим модулем» дает в упругопластический области несколько завышенные значения критических напряжений.

На рисунке 2 построена кривая, ординаты который вычислены по формуле (3) с касательным модулем. Здесь же темными точками отмечены результаты опытов, полученные для материала, близкого по механическим свойствам к Д 16Т. В упругой области эти точки почти в точности совпадают с гиперболой Эйлера; в пластической области точки следует примерно кривой касательного модуля.

Формула (3) дает результаты, лучше согласующиеся с результатом опытов. Так как величина E меньше T , то критические напряжения, найденные с помощью касательного модуля, всегда оказываются меньше, чем определенные по результирующему модулю.

Если потеря устойчивости стержня происходит за пределом упругости, то нормальные напряжения, как в зоне догрузки, так и в зоне разгрузки, будут пропорциональны не модулю упругости, а секущему модулю, который сам зависит нелинейным образом от продольных деформации в рассматриваемой точке, в соответствии с диаграммами «напряжение-деформация».

Приведем краткое решение замечательной задачи «О критической силе в сжатом стержне» доктором техническим наук, профессором И.С. Цурковым [1].

Диаграмма сжатия т = f (e) имеет вид, показанный на рисунке 3. На диаграмме выделяются два участка: первый участок, представленный наклонной прямой OA, выражающей закон Гука, а второй, представлен кривой AB , что соответствует нелинейной зависимости между напряжениями и деформациями при наличии упрочнения материала. Точка M на диаграмме – точка бифуркации равновесного состояния сжатого стержня, ε - критическая деформация, σ - критическое напряжение. В момент разветвления равновесных состояний придадим стержню бесконечно малое изгибное возмущение, характеризуемое бесконечно малой функцией кривизны  Δk и соответствующей ей бесконечно малой функции прогиба Ay : Ae = Akz; A к =

d ² A y dx ² ’

ось Z направлена вниз.

Стержень принят за шарнирно-опертую балку, у которой под действием указанного бесконечного малого изгиба нижние волокна растягиваются, а верхние сжимаются. Тогда в части поперечного сечения, которая расположена выше нейтральной оси, будут иметь место догрузки, а в нижней части поперечного сечения будет разгрузка.

Предполагаем, что догрузка идет по кривой MB диаграммы (рисунок 3), а разгрузка на прямой наклонной MC , которая параллельна OA .

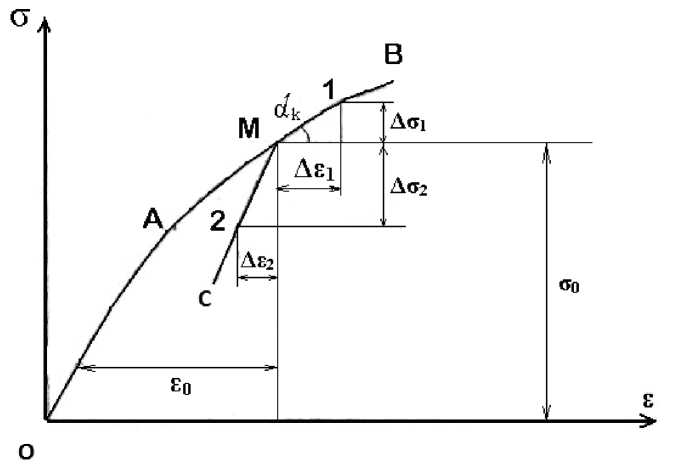
Рисунок 3. Диаграмма сжатия

Для зоны 1, расположенной выше нейтральной оси имеем:

Ат = T — Т; Ag\ = ExAex ;

где E - касательный модуль в точке M .

Для зоны 2 – зоны разгрузки:

Δσ = E Δε ;

где E - тангенс угла наклона линии разгрузки (рисунок 3).

Таким образом, зависимость между напряжениями и деформациями в точках поперечного сечения стержня при бесконечно малом изгибном возмущении определяется прямой М – 1 в зоне догрузки и прямой М – 2 в зоне разгрузки (рисунок 3).

Таблица 1. Модули и гибкости для стержня двутаврового сечения из дуралюмина Д16Т

№	Точк и на диаг рам ме	Относите льная деформа ция ε ⋅ 10 3	Напряж ение σ МПа	Касател ьный модуль E k ⋅ 10 - 4 МПа	Результ ирующи й модуль T ⋅ 10 - 4 МПа	Модуль Цурков Ц ⋅ 10 - 4 МПа	Гибкос ть λ	λ ц	σ k	σ T	σ ц
1	a	2,67	200	7,5	7,5	7,5	60,5	60,5	200	200	200
2	b	3,0	220	5,96	6,65	6,85	54,7	57,5	210	220	215
3	c	3,5	246	4,34	5,50	6,06	47,0	48,2	238	250	245
4	d	4,0	264	3,72	4,97	5,05	43,0	45,7	245	270	252
5	e	4,5	278	2,55	3,81	4,05	36,3	37,6	252	260	254
6	f	5,0	290	2,05	3,22	3,80	33	35	254	281	260
7	g	6,0	308	1,5	2,5	3,63	28,5	34,3	275	307,5	291,6
8	h	7,0	320	1,17	2,03	3,4	25,1	32,6	285	318,7	306,0
9	i	8,0	332	0,97	1,72	3,18	22,75	30,9	310	331,9	320,0
10	k	9,0	340	0,82	1,48	2,9	20,8	27,5	320	330	326
11	l	10,0	345	0,82	1,48	2,9	20,6	25	331	328	324
12	m	11,0	356	0,82	1,48	2,9	20,2	23	334	338	323
13	n	12,0	364	0,82	1,48	2,9	20	21	333	345	335

Отношение полного напряжения к полной деформации в точках указанных прямых дает значение секущего модуля в этих точках; секущий модуль в зоне догрузки обозначим через ψ , а в зоне разгрузки через ψ . Для определения секущих модулей имеют место формулы:

σ

ψ ₁ =   ¹

ε

σ + Δσ ε + Δε

^{σ 0} (1 + ^{Δ σ 1})[1 - ^{Δ ε 1} + ( ^{Δ ε 1})² - ...] ε ₀      σ ₀       ε ₀     ε ₀

σ σ + Δσ σ   Δσ   Δε  Δε

ψ 2 =   ² =   ^{0      2} =   ⁰(1 +     ²)[1 -     ² + (   ²)² - ...]

ε ₂₁    ε ₀ + Δ ε ₂    ε ₀      σ ₀       ε ₀      ε ₀

Ввиду малости величин Д е / Д ^ , Д е / Д е по сравнению с единицей в формулах (8) и (9), расположенных в квадратных скобах, оставляем только первые степени; тогда указанные формулы принимают вид:

V 1 = V о [1 +— (1 - —)]; z ^ 0, е о      V о

Δkz   E v 2 = v о[,+—(1 - —)]; z ^ о. ео     V о

Здесь через V o обозначен секущий модуль точки бифуркации М ; он задан, и определяется выражением:

^а о    Ф ^{( е} о )

^е о       ^е о

После того, как сжатый стержень потеряет устойчивость, т.е. перейдет в состояние бесконечно малого изгиба, в сечениях стержня кроме сжимающей силы N будет иметь место бесконечно малый изгибающий момент Д М , при этом продольные деформации и нормальные напряжения в точках поперечного сечения определяются формулами:

е = е + Д kz,

а = v ( e + Д к² ).

В формуле (14) через ψ обозначен секущий модуль, выражение которого для зоны догрузки определяется формулой (10), а для зоны разгрузки – формулой (11).

Пользуюсь (13) и (14) записываем выражения для бесконечно малого изгибающего момента и сжимающей силы:

σ zdF = ε ∫ ψ zdF + Δ k

ΔM=∫

J v z ² dF ;                          (15)

FFF

ДN = J adF = е JvdF + ДкJVz dF.

F _FF

Вводя обозначения, предложенные А.А. Ильюшиным

Ix =JvdF; 12 =JyzdF; I3 =Jvz2dF;

FFF формулы представим в виде:

ДМ = ДМ3 + е 12;

N = kI +Д kI2.(19)

Функции I_v , I ₂, I ₃ выражают собой жесткости поперечного сечения стержня, деформируемого при совместном изгибе и сжатии за пределом упругости; функция I является жесткостью при сжатии; I -жесткостью при изгибе; I - смешанной жесткостью.

В соответствии с (9), (10) и (16) для указанных жесткостей получаем формулы:

I , = V о F + ^{Д к} V о ( S , + S 2 ) -~ ( E , S 1 + E 2 S 2 );

^е о

^е о

	1 2 = у о ( s , + s 2 ) + — У о ( В , + В 2 ) — ^ k ( E , В , + E 2 В 2 );                    (21) Е о                  Е о 1 3 = у „ ( В , + В 2 ) +^ k V „ ( С , + С 2 ) —^ k ( E , С , + E 2 С 2 );                     (22) Е о                  Е о
где	s = J zdF ; s2 = j zdF ; В, = J z 2 dF ; В2 = j z 2 dF ;                         (23) F               F 2                F ,                  F 2 С = J z 3 dF ; С2 = J z 3 dF .                                   (24) F                 F :

В этих формулах S S - статические моменты площадей зоны догрузки и зоны разгрузки относительно оси y , В_х , В₂ - осевые моменты инерции тех же площадей относительно нейтральной оси; С_х , С₂ - новые геометрические характеристики, определяемыми выражениями (20 - 22).

Запишем основное уравнение (18) с учетом соотношений (20 - 22):

Δ k

А М = А к [{ у ( В_х + В₂ ) + — ( С , + С ₂)

Ео

— — ( E , С , + E ₂ С 2 )} + е о { у о ( S 1 + S 2 ) + — V о ( В , + в 2 ) — — ( E , В , + E 2 В 2 )}. "( ²⁵⁾

^Е о

^Е о

^Е о

Из этого уравнения следует, что если кривизна А к, то и момент АМ функции бесконечно малые, и величина S, + S2, представляющая собой статический момент поперечного сечения должна быть бесконечно малой, поэтому нейтральная ось должна проходить через центр тяжести поперечного сечения.

Это условие будет выполнено только в том случае, если разгрузка в начальной стадии, когда сжатый стержень подвергается бесконечно малому изгибу, будет проходить по плавной кривой М — 2 , а не по наклонной прямой М — 1 .

Следовательно, к точке М слева подходят две кривые: кривая AM , уравнение которое ст = F ( е ) и кривая разгрузки 2 — М , уравнение которой запишем в виде т = f ( е ) . Эти кривые в точке М имеют общую касательную, тангенс наклона которой E есть касательный модуль.

Зависимость между приращениями Δ σ и Δ ε была получена ранее, она представлена формулой (6); формула (7), которая связывает приращения Δ σ и Δ ε , относящиеся к точке 2, должна быть заменена.

Значение функции т = f ( е ) запишем в виде ряда Тейлора через значения, который принимает она и ее производные в точке разветвления M .

df         ( е ₂ — Е _о)² d ² f

Т2 = f (Ео ) + (Е2 — Ео ) ,  (Ео ) +      2       , 2 (Ео ) + ...

dE         2

Так как f ( е₀ ) = F ( е ) = т ₀, то

Л               /      х db  х Е — Е )² d ² f z х      Л 2 df . х   ( А е₂ ) d ² f, _х

Ат, = т, — т0 = (Е — Е )~(е0 ) + —---о--т(е о) +... = Ае 2—(е ) + -—2--Е(е) +...

2      2      и       2     и          и                          2     о                         о2 dE         2    dE             dE       2

Отбрасывая величины более высокого порядка малости по сравнению с первым членом ряда (15)

и учитывая, что — ( е ) = E i , получаем: d ε

Ат = Ei Ае .

В начальной стадии разветвления равновесного состояния сжатого стержня догрузка и разгрузка идут по касательной в точке M ; нейтральная ось еще не успевает сместиться и проходит через центр тяжести поперечного сечения. Уравнения записывается в форме уравнения устойчивости Эйлера:

y + +--—----- A y = 0, где у ₀ = -°- - секущий модуль точки бифуркации M ;

dx (2Уо - Ei)Jy

J = B + B - осевой момент инерции поперечного сечения относительно нейтральной оси, обозначения которых предложены А.А. Ильюшиным [2], E - касательный модуль упругости.

Вводим обозначения:

, 2_     N    _    -0    .

k                                                  ;       ==

(2 у ° - E i )J -   (2 у ° - E i ) i 2   Ц A

Ц = (2^ - Ех) - модуль Цуркова, получим

^σ кр

п ² Ц ^ Ц

Вывод этой формулы опирается на уравнение, связывающее изгибающий момент и кривизну при изгибе сжатого стержня в рамках деформационный теории пластичности. Оно является частным случаем более общих зависимостей, построенных для тонких оболочек А.А. Ильюшиным.

В таблице приведены величины E , T , Ц соответствующие ряда значений напряжений σ и относительной деформации сжатия ε .

На рисунке 2 построены кривые, ординаты которых вычислены по формулам (3, 5, 27).

Здесь же темными точками отмечены результаты опытов, полученные для материала, близкого по механическим свойствам к Д 16 Т. В упругой области эти точки почти в точности совпадают с гиперболой Эйлера. Показаны кривые Энгессера, Кармана. Кривая Цуркова, проходит в вилке этих кривых прерывистой линией.

Выводы и заключение:

• 1.    Критическое напряжение, определенное по результирующему модулю, дает верхний предел для несущей способности сжатого стержня;

• 2.    Напряжение, найденное с помощью касательного модуля, определяет нижний предел;

• 3.    Напряжение, определенное по модулю Цуркова, расположено в вилке, и дает более точные данные. В строительстве инженерных сооружений при использовании облегченных по весу тонкостенных конструкций расчет по предложенной методике, дает экономию в строительных материалах и прогноз надежности при работе конструкций за пределом упругости.

При исследовании устойчивости сжатого стержня за пределом упругости надо привлекать законы деформационной теории пластичности, что дает полное представление о работе конструкции и позволяет в любой момент нагружения вскрыть неиспользованные резервы прочности.