Устойчивость закритического деформирования при кручении толстостенного цилиндрического тела

PNRPU MECHANICS BULLETIN

Проведение уточненного прочностного анализа конструкций требует изучения вопросов зарождения и развития зон неупругого деформирования, возникающих вследствие равновесного накопления повреждений. Данный процесс находит отражение на диаграмме деформирования материала в виде ниспадающей ветви, характеризующейся снижением уровня напряжений при растущих деформациях и являющейся геометрическим местом точек, соответствующих достижению предела прочности [1–9]. Необходимым условием устойчивой реализации закритической стадии деформирования является достаточная жесткость нагружающей системы [10–12]. С помощью установок высокой жесткости полная диаграмма деформирования материала может быть получена экспериментально [13–15].

Учет разупрочнения материала при анализе различных конструкций позволяет выявить дополнительные прочностные и деформационные резервы [16; 17]. Получен ряд аналитических решений краевых задач механики закритического деформирования. В работе В.А. Ибрагимова и В.Д. Клюшникова решены задачи чистого изгиба балки и деформирования сферической полости в пространстве, нагруженной равномерно распределенным давлением [18]. В исследовании Л.В. Никитина и Е.И. Рыжака рассмотрена задача о всестороннем сжатии горных пород [19]. В работе С.Д. Волкова, Г.И. Дубровиной и Ю.П. Со-ковнина приведена задача растяжения пластины с поперечной трещиной [20]. В исследовании В.В. Стружанова решена задача о разрушении диска с ослабленной цен- тральной зоной [21]. В работах В.Э. Вильдемана рассмотрены задачи трехточечного изгиба балки, разрушения толстостенного цилиндра под действием внутреннего давления, кручения цилиндрического тела с учетом разупрочнения, задачи механики закритического деформирования стержневых систем [10; 22–23].

Вопросы кручения неупругих тел различного сечения и пересчета диаграмм нагружения при кручении на истинную диаграмму деформирования при сдвиге рассмотрены в работах Е.В. Ломакина [24; 25], В.В. Стру-жанова и Е.Ю. Просвирякова [26–30], В.П. Радченко [31; 32], Н.Х. Арутюняна и Ю.Н. Радаева [33; 34], В.Г. Баженова [35; 36], Б.Г. Миронова и других авторов [37–41]. В ряде работ представлены полученные экспериментально диаграммы нагружения металлических образцов при кручении с выраженным участком разупрочнения.

Данная работа является продолжением рассмотренной авторами ранее задачи кручения цилиндрического тела при жестком нагружении с учетом разупрочнения [22]. Рассмотрена задача кручения толстостенного цилиндрического тела с учетом закритической стадии деформирования материала и жесткости нагружающей системы, представляющей собой соединенный последовательно с телом упругий элемент.

• 1.    Постановка задачи

Рассмотрим полый осесимметричный стержень длины L с наружным диаметром D и внутренним диаметром d = aD, ae[0;1) в цилиндрической системе координат. Один торец стержня закреплен, ко второму через упругий элемент с жесткостью на кручение Rф прикладывается момент, обеспечивающий угол поворота ф0. Массовые силы не рассматриваются. Схема изображена на рис. 1.

Из выражений (2), (3) и (6) следует, что угол сдвига определяется как

ф

Y 0 z = ri: •

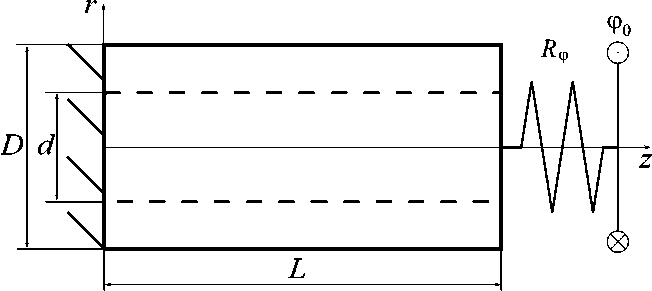
Рис. 1. Схема нагружения полого цилиндрического тела

Из равенства внешних и внутренних силовых факторов следует

D /2      ₂

^M = L /2 ^{2 n} r ^T 0 z ( r ) ^dr •

Связь между углами поворота ф _L и ф ₀ примет вид

M ф0 =ф L + —• R ф

Fig. 1. Loading scheme of the hollow cylindrical solid

В силу симметрии, наличия одного силового фактора – крутящего момента M и выполнения гипотезы плоских сечений, две компоненты вектора перемещений являются нулевыми, третья компонента не зависит от окружной координаты:

U ( r , 0 , z ) = 0; u_z ( r , 0 , z ) = 0; u _e ( r , 0 , z ) = u _e ( r , z ) . (1)

Условие устойчивости процесса деформирования может быть получено из следующих соображений: при активном нагружении положительному приращению угла поворота ф ₀ должно соответствовать положительное приращение угла поворота торца стержня ф _L . В таком случае при использовании выражения (9) получаем условие устойчивости, связывающее жесткость нагружающей системы R _ф с собственной жесткостью стержня:

При выполнении гипотезы о сохранении радиусов сечений прямыми связь между компонентой вектора перемещений u ₀( r , z ) и углом поворота сечения ф ( z ) является линейной:

d фo. >  0 ^ 1 + Л dM ^d ф L          ^R ф ^d ф L

> ⁰ ^ dM >- ^R ф • d ф l

u о ( r , z ) = r ф ( z ) .                    (2)

В таком случае компоненты тензора деформаций ^e rr = ^£ 00 = ^£ zz = ^Y r 0 = Y rz = 0,

Таким образом, в задаче с использованием выражений (4), (7), (8)–(10) определяются связь крутящего момента с углом закручивания системы и распределение напряжений по поперечному сечению стержня.

d u ₀ ( r , z ) Y =--—---

^Y 0 z

d z

d ф ( z ) dz

2. Кручение стержня из материала с двухзвенной кусочно-линейной полной диаграммой деформирования

Единственная ненулевая компонента тензора напряжений с использованием функции пластичности Ильюшина [42] будет записана в виде

Закон связи между касательным напряжением и сдвиговой деформацией выбирается кусочно-линейным:

^T 0 z = G ( 1 -w ( Y 0 z ) ) Y 0 z .                ⁽⁴⁾

G Y 0 z , ⁰ ^Y 0 z y ;

^T 0 z = 1 ^G Y y ^- D G ( Y 0 z ^- Y y ) , Y y ^ Y 0 z < Y f ;

Здесь G – начальный модуль сдвига материала. Три уравнения равновесия вырождаются в одно:

⁰- Y f ^Y 0 z

^dto(Y 0 z )    ) dY 0 z

' ° z

Эт             (      , x

'Y = 0 ^ G 1 -®(Y, z)- oz d2ф(z)

Л = 0.

dz

Обозначим угол поворота сечения на правом торце ф( L) = фL , в таком случае с учетом граничных условий решение дифференциального уравнения (5) имеет вид здесь Yy — угол сдвига, соответствующий началу пластических деформаций; Yf — угол сдвига, соответствующий полной потере несущей способности; DG – модуль разупрочнения при сдвиге. Соотношения (11) обеспечивают проиллюстрированную на рис. 2 двухзвенную кусочно-линейную аппроксимацию полной диаграммы деформирования. Также для удобства дальнейших расчетов введем обозначение

ф ( z ) = L Ф L •

-= G + D G

G

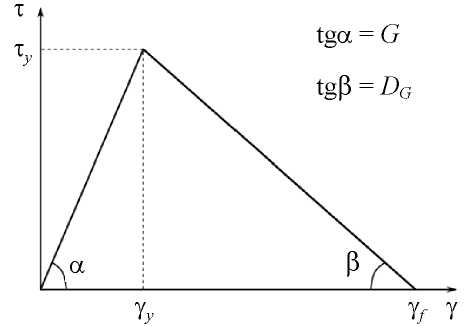
Рис. 2. Двухзвенная кусочно-линейная аппроксимация полной диаграммы деформирования

1 – стадия упругого деформирования. На данной стадии ϕ _L < ϕ _y , связь крутящего момента с углом закручивания торца является линейной:

M ϕ L

= .

M y  ϕ y

2 – стадия начальной закритической деформации. 1 λ

Здесь ϕ ≤ ϕL< ϕ и ϕL < ϕ . Момент зависит y α y         λ-1 y от угла поворота правого сечения следующим образом:

Fig. 2. Two-link piecewise linear approximation of the complete deformation diagram

Пусть начало пластического деформирования происходит при крутящем моменте M_y и угле поворота правого торца ϕ _y ; обозначим собственную жесткость стержня при кручении в упругой области R_L , тогда из (7), (8) и (11) следует

M y = ^π ₁ ^D ₆ ³ ( 1 -α ⁴ ) G γ y ;

2 γ _yL ϕ y = _D ^y ; R

My

=    =      1-α4 G.(13)

Lϕy 32 ()

M

M y

.Г 1 I ф L* 1 -%---4 I+

^{1 -a} ) ф ,

ϕ

+⁴ x —4 - - x —Цт I -I.

3 1 - a ⁴ 3 1 - a ⁴ ( ф _L )

(16а)

Данная функция имеет на исследуемом промежутке точку максимума

ϕ _L λ

= 4                  .

ϕ _y λ- ( 1 -α )

(16б)

Максимальное значение крутящего момента:

В таком случае выражение (8) с учетом (7), (11)–(13) принимает вид

2 Р У )    „4           ( 2 Р f )    ( 2 Р У )

-α            -

D ϕ 4 DD = ^L + λ

M_y 1 -α ⁴ ϕ _y 31 -α ⁴

M ^*

M y

31 -α ⁴

(- -1,-           I

X-X ⁴ ( X- ( 1 -a ⁴ ) ) ⁴

Условие устойчивости примет вид

(16в)

2 ρ _f

R _{ϕ ≥ λ}

-

-(λ-1)

D

D

ϕ L

R L

1 1 -α ⁴

(

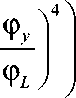
- 1.

(16г)

1 -α ⁴

ϕ y

	1, ф l <ф y ;
2 ρ y = D	ф y              1 , ϕ y ≤ϕ L <ϕ y ϕ L          α

α , ¹ ϕ _y ≤ϕ _L ; α

	L , x 1, ф L ^ ФУ;
2 ρ f	X ф y   X    „	λ 1 <ϕ y
=
D	X- 1 ф L X- 1 y L c X 1    , „ Г X- 1 «ф5ф L ’	λ- 1 α

Далее, в зависимости от соотношения между геометрией стержня и свойствами материала, возможна реализация двух различных сценариев развития зон неупругого деформирования.

3.1 – стадия начального разрушения. На данной λ 1

стадии ϕ ≤ ϕL< ϕ , связь крутящего момента с λ-1        α углом закручивания рассчитывается по формуле

M     a 4 ф L 1 v	(X'	3 I	3 1 ( фу I          .
=      4   + X M y    1 -a4 ф y  3	V X- 1 v	- 1 )	,      41 y I • (17а) 1 -a V ф L )

Данная функция является монотонно убывающей.

Условие устойчивости:

где ρ _y , ρ _f – расстояния от центра сечения до границы зоны разупрочнения и зоны с потерявшим несущую способность материалом соответственно.

R ϕ _≥ α 4

R_L 1 -α ⁴

((

+ X

X I ³

X - 1 )

- 1

)

1 1 -α ⁴

*I.

Ф L )

(17б)

3.2 – стадия развитой закритической деформации. Диапазон углов поворота торца определяется неравенст-

1             X вом —ф < фL < =—ф , выражение (14) принимает вид a y X-1 y

— = (1 -X)

M y

ф ^ ₊ 4 x 1^.

ф y  3 1 -a ⁴

(18а)

Функция является линейной и монотонно убывающей, условие устойчивого закритического деформирования:

R^ >X- 1.

R L

(18б)

После любого из сценариев развития неупругих зон (стадия 3.1 либо 3.2) деформирование продолжается по единому варианту.

4 – стадия развитой закритической деформации и раз-

X              1 X          1

рушения. Здесь ^—ф y <ф L <-^— ф y и   ф y <ф L ,

X- 1         aX- 1      a

связь момента с углом закручивания имеет вид

M          a ⁴ ф l 4_T a ³

m ; =l^x-¹) гф? ф ; " 3^X1-^

¹ X

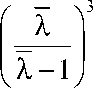
^ф y

I I "

^{1 -a} l Ф L )

(19а)

Функция монотонно убывает, имеет соответствующий правой границе рассматриваемого промежутка минимум, в котором момент становится равным нулю и происходит полная потеря несущей способности. Условие устойчивости:

R

R - >- ( X- 1 )

R L

a ⁴

1 -a ⁴

i X - 1 _v

-^-I     I .

-a ⁴ 1ф _L J

(19б)

Анализ решения. Эпюры распределения напряжений по сечению для различных стадий деформирования приведены на рис. 3.

На рис. 4 приведены диаграммы нагружения в относительных координатах для различных наборов значений параметров X и a . На рис. 5, а , и b , приведены иллюстрирующие выражения (16в) и (16г) поверхности зависимости максимального значения крутящего момента и экстремального значения угла поворота торца стержня от его геометрии и свойств материала. Анализ показывает, что при снижении модуля спада материала и внутреннего диаметра стержня происходит рост максимального крутящего момента и соответствующего ему угла закручивания. Из графиков видно, что учет закритической стадии деформирования позволяет выявить значительные прочностные и деформационные резервы рассматриваемой конструкции.

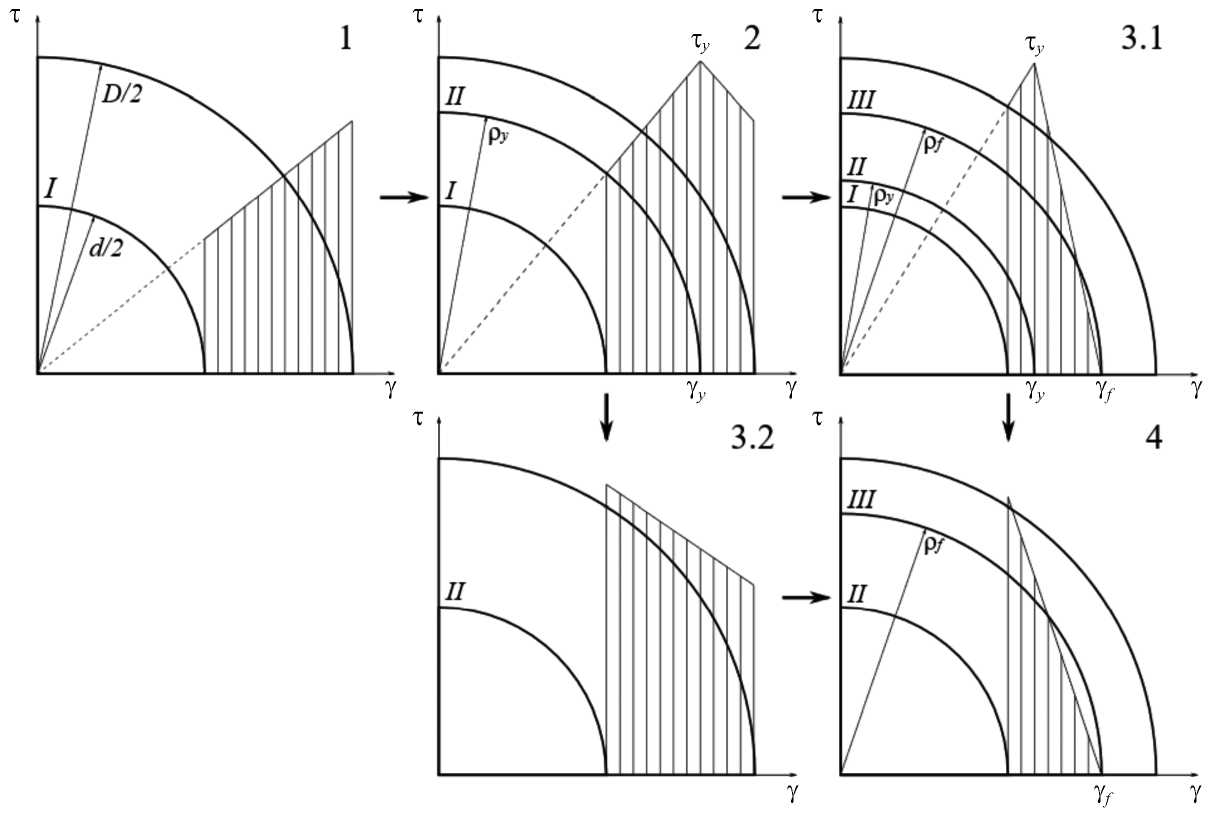
Рис. 3. Эпюры распределения напряжений

Fig. 3. Stress distribution diagrams

Анализ выражений (16г), (17б), (18б), (19б) позволяют сформировать условие реализации полной диаграммы нагружения, т.е. определить необходимую жесткость нагружающей системы:

R ϕ_≥ R L

<

λ

λ - 1

λ

1 -α ⁴

- 1, ^λ ≤ ¹; λ - 1 α

λ - 1,

1 λ

< .

α λ- 1

Иллюстрация данной формулы приведена на рис. 6, а . На рис. 6, b , представлена диаграмма нагружения в виде зависимости крутящего момента от задаваемого угла поворота ϕ ₀ для различных значений нагружающей системы, указаны точки срыва с диаграммы нагружения. Продемонстрирована необходимость учета свойств нагружающих систем в расчетах конструкций.

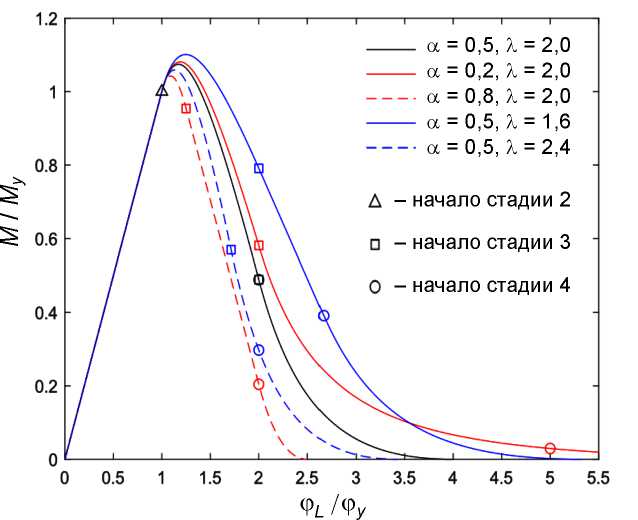
Рис. 4. Диаграммы нагружения

Fig. 4. Loading diagrams

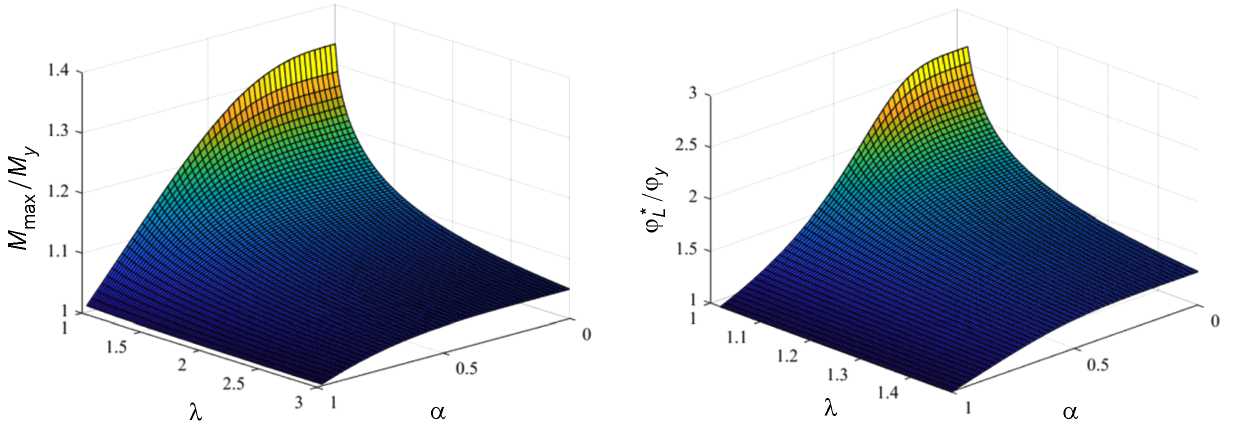
а

b

Рис. 5. Зависимость максимального значения крутящего момента ( а ) и соответствующего угла закручивания ( b ) от параметров материала и геометрии стержня

Fig. 5. Dependences of torsion moment maximum value ( а ) and corresponding value of rotation angle ( b ) on material parameters and geometry (in relative coordinates)

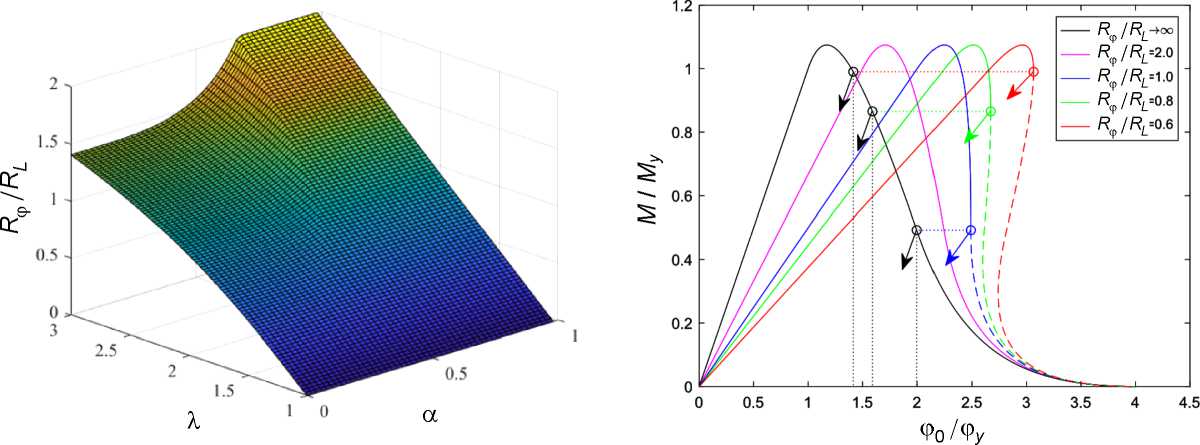
а                                                     b

Рис. 6. Зависимость требуемого значения жесткости нагружающей системы для реализации полной диаграммы нагружения от параметров материала и геометрии стержня ( а ); вид диаграмм нагружения при различных значениях относительной жесткости нагружающей системы ( b )

Fig. 6. Dependence of the loading system stiffness required value for the complete loading diagram implementation on the material parameters and rod geometry ( а ); loading diagrams for various values of the loading system relative stiffness ( b )

3. Кручение стержня из материала с трехзвенной кусочно-линейной полной диаграммой деформирования

Закон связи между касательным напряжением и сдвиговой деформацией:

2 ρ y D

'G Y e z , 0 — Y e z y ;

G y + G' ( Y e z -Y y ) , Y y -Y e z в ;

( G - G ' ) Y y + G ' Y в - D G ( Y e z -Y в ) , Y в ^ Y e z < Y f ;

0, Y f — Y e z .

1, ϕ _L <ϕ _y ;

ϕ _y               1

, ϕ _y ≤ϕ _L <ϕ _y ;

ϕ _L          α

α , ϕ _y ≤ϕ _L ;

α

2 p B = _<

D '

здесь γ _B – угол сдвига, соответствующий пределу прочности и началу стадии разупрочнения; G ' – модуль упрочнения при сдвиге. Соотношения (21) обеспечивают проиллюстрированную на рис. 7 трехзвенную кусочнолинейную аппроксимацию полной диаграммы деформирования. Введем обозначения

• 1, ϕ _L <βϕ _y ;

• β^{ϕ y} , βϕ _y ≤ϕ _L < ¹ βϕ _y ;

^ϕ L            ^α

• α , ¹ βϕ _y ≤ϕ _L ;

α

2 p f

=

D

G - G '      γ _B       γ f βλ+ ( 1 -β ) κ

κ = _G , β= _{γ y} , χ= _{γ y} = _{λ- 1}

1, ϕ _L <χϕ _y ;

ϕ _y                1

χ , χϕ _y ≤ ϕ _L < χϕ _y ;

ϕ _L           α

α , ¹ χϕ _y ≤ϕ _L , α

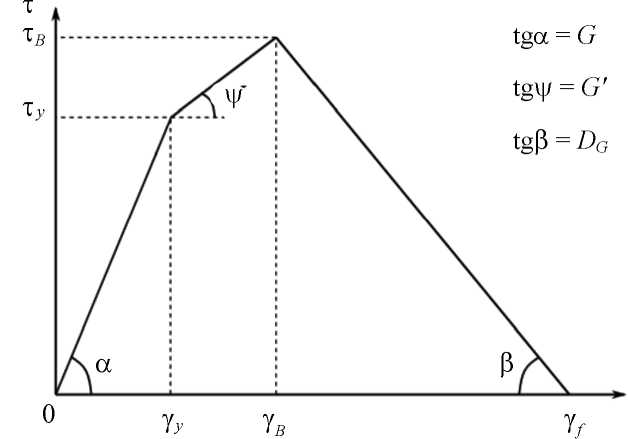
Рис. 7. Трехзвенная кусочно-линейная аппроксимация полной диаграммы деформирования

где ρ _y , ρ _B – расстояния от центра сечения до границы зон упрочнения и разупрочнения соответственно.

1 – стадия упругого деформирования. На данной стадии ϕ _L < ϕ _y , связь крутящего момента с углом закручивания торца аналогична выражению (15).

–

стадия начального упрочнения. Здесь

ϕ ≤ ϕL< ϕ и ϕL < βϕ . Момент зависит от угла yLαy L y поворота торца следующим образом:

M (

= 1 -κ

M y I

1     ) Ф L

1 - a ⁴ J ф y 3 1 - a ⁴

-κ 31 -α ⁴

ф , I

- I . (24)

Ф L J

Fig. 7. Three-link piecewise linear approximation of the complete deformation diagram

Выражение (8) с учетом (7), (12), (13), (21), (22) принимает вид

2 ρ y

-

M

D

α ⁴

ϕ _L

2 ρ _B

-

2 ρ y

Данная функция является монотонно возрастающей.

В зависимости от соотношения между параметрами материала и геометрией стержня деформирование будет реализовываться по различным сценариям развития зон неупругого деформирования.

3.1 – стадия начального разупрочнения. На данной стадии угол закручивания стержня удовлетворяет нера-1

венствам βϕ ≤ ϕL< ϕ и φL< χφ, зависимость мо-y         αy             y мента от угла закручивания:

M y

1 -α ⁴

ϕ y

+

D

D

ϕ _L

1 -α ⁴

ϕ y

+

= ( i -x      I Ф-

M y I 1 ^-a J ф y

1 1 -α ⁴

-

2 ρ _f

-

2 ρ B

(25а)

(1-λ)

D

D

ϕ L

1 -α ⁴

+

κ

ϕ y

2 ρ _f

D

-

2 ρ y

D

1 -α ⁴

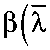
2 ρ _f

D

-

2 ρ B

D

1 -α ⁴

;

При < χ данная функция является монотонно α возрастающей. Иначе данное выражение обладает точкой максимума

ф . _ ^в 4 ^Х+ ( ‘ -^в 4 ) ^к

4 Х- ( 1 -а ⁴ ) ’

(25б)

Данная функция имеет на исследуемом промежутке точку максимума

в которой принимает значение

M ^*

M y

3 1 -а ⁴

(х(х-1)-

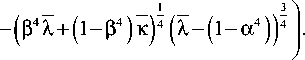
(25в)

В таком случае требуется условие устойчивости:

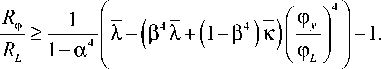
(25г)

3.2 – стадия развитого упрочнения. Угол закручи вания торца лежит в диапазоне — ф < фL < —ф , выра-а y          y

жение (23) принимает вид

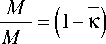
ф,   4-1 -а ³

—+-к----.

ф y 3 1 - а⁴

Функция является монотонно возрастающей.

4.1 – стадия начального разрушения. На данной стадии Хф < фL < — ф , крутящий момент рассчитыва-у а у ется по формуле

М _   а ⁴ ф _L

M y   1 -а ⁴ ф у

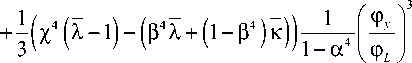
(27а)

Данная функция на рассматриваемом промежутке является монотонно убывающей; условие устойчивости закритического деформирования:

R^ >^^

R_l  1 -а⁴

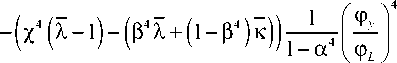
(27б)

4.2 – стадия развитого упрочнения и начального ра зупрочнения. Здесь Рфy < ф. < в—фy, — фy < ф. < Хфу, а а связь момента с углом закручивания имеет вид

M

M y

1 -к-

Х-к 1 1 -а ⁴ )

ф . ₊ ф у

1 -а ⁴

- 3 в ⁴ ( ^х-^к )

1 -а ⁴

ф У 1

(28а)

I ф L

Ф. о Х-к фу Р 4 (Х-1) + (1 -к)а4"

(28б)

Максимальное значение крутящего момента на данной стадии:

M ^*

M y

хг^ №-‘W -

1/Z-                 Х3 1

^-в ( ^Х-к ) 4 ( ( ^Х- ‘ ) + ( ‘ ^-к )^а4 )⁴

J

Условие устойчивости:

R^ >(Х-к) V R_l ⁽ ) 1 -а⁴

1 -в ⁴

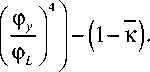
(28г)

(28в)

5.1 – стадия развитого упрочнения и начального разрушения. Угол закручивания торца лежит в диапазонах

— ф <ф _L <— ф и Хф <ф _L , крутящий момент равен а ^у а ^{у у}

M           а⁴ ф, 4- а ³

--_- ( 1 -к )--- т .-- — к----

Му ' Ч -а ⁴ ф _у 3 1 -а ⁴

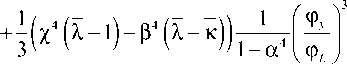
(29а)

Данная функция является монотонно убывающей; достаточная жесткость нагружающей системы определяется неравенством:

R

а ⁴

1 -а ⁴

R L

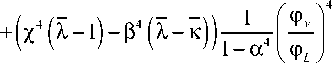
(29б)

5.2 – стадия развитого разупрочнения. На данной стадии — ф < фL < Хф , выражение (23) принимает вид а у           у

M

M y

_- ( Х- 1 ) 2 . + 4 Х ( Х- ‘ ) 12 21.

'     ’ ф _у 3 ^х Ч - а⁴

(30а)

Функция является монотонно убывающей. Условие устойчивости:

R ^(Х-1).

(30б)

6 – стадия развитой закритической деформации и разрушения. Здесь Хфу < фL < ~ХфУ и —фу < фL , связь у а у а у момента с углом закручивания имеет вид

4           a ³

- 3x(X-0     +

M -R- 1 ^a 4 ^ .

M y '   Ч-а ⁴ Ф y

(31а)

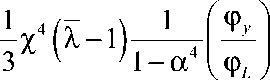
Функция (31а) монотонно убывает, аналогично (19а) имеет соответствующий правой границе рассматриваемого промежутка минимум, в котором крутящий момент становится равным нулю и происходит полная потеря несущей способности. Закритическое деформирование является устойчивым при выполнении условия

— I . (316)

Ф _L 7

Из выражений (25в) и (28в) следует, что максимальное значение крутящего момента определяется выражением

31^1 0 4 №^{- 1 )-}

- ( p ^{4 X} + ( 1 -P ⁴ ) ^K ) ⁴ ( X- ( 1 -a ⁴ ) ) ⁴ '

M ^*

M y

x^ ;

a

3T^ ^{(x(I- 1 )-Ka} 3 ^-

1/,-                 X3 )

• -р ( Х-к ) ⁴ ( ( X- 1 ) + ( 1 -к ) ⁰ )⁴

  
  

  Анализ решения. Эпюры распределения напряжений по сечению для различных стадий деформирования приведены на рис. 8.

  
  
  
  

  - -

  
  

  I a

  
  
  

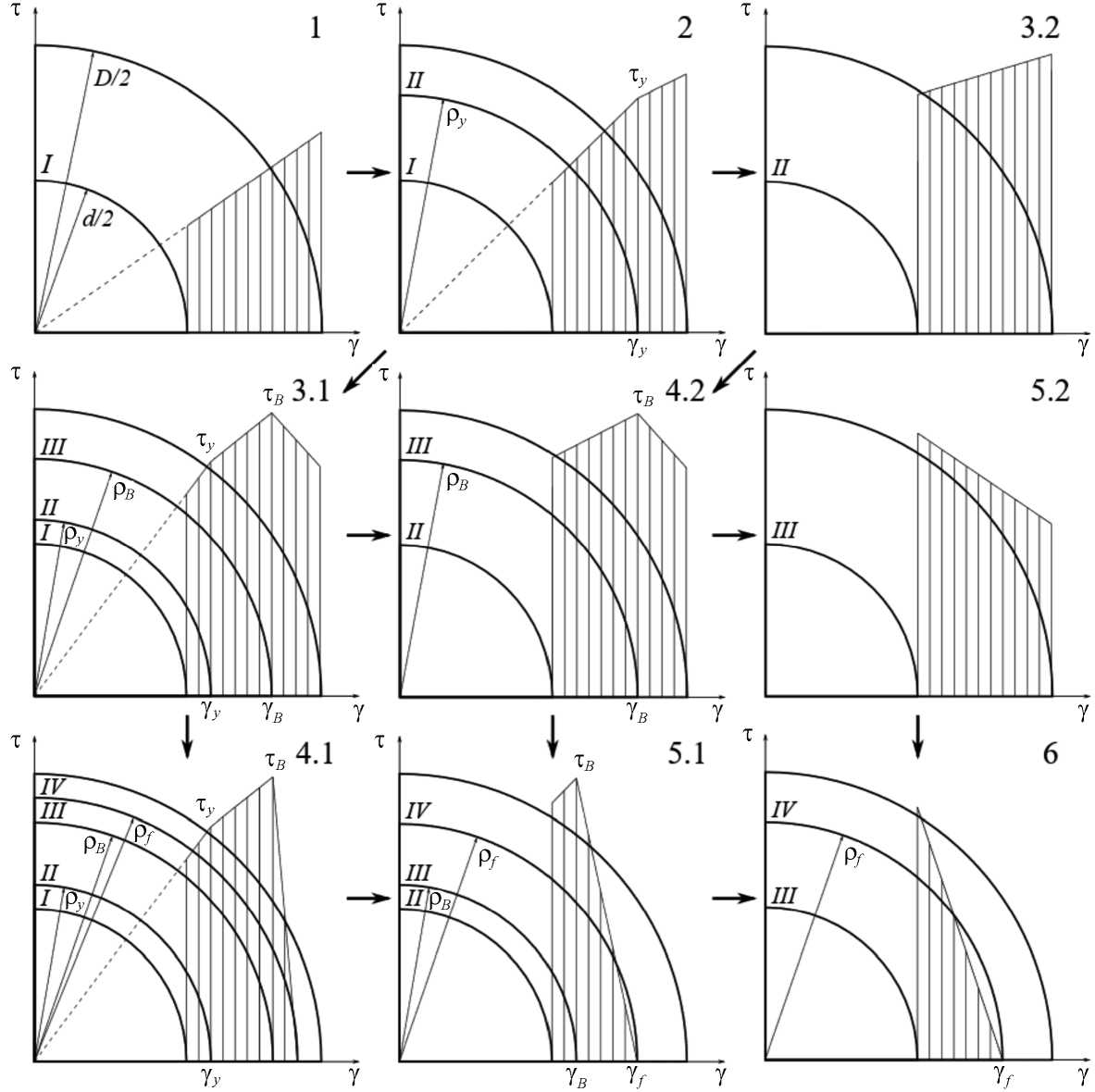
  Рис. 8. Эпюры распределения напряжений

  Fig. 8. Stress distribution diagrams

  
  

  ^д - начало стадии 2

  □ - начало стадии 3 .

  о - начало стадии 4

  О - начало стадии 5 _

  s - начало стадии 6

  

  d

  c

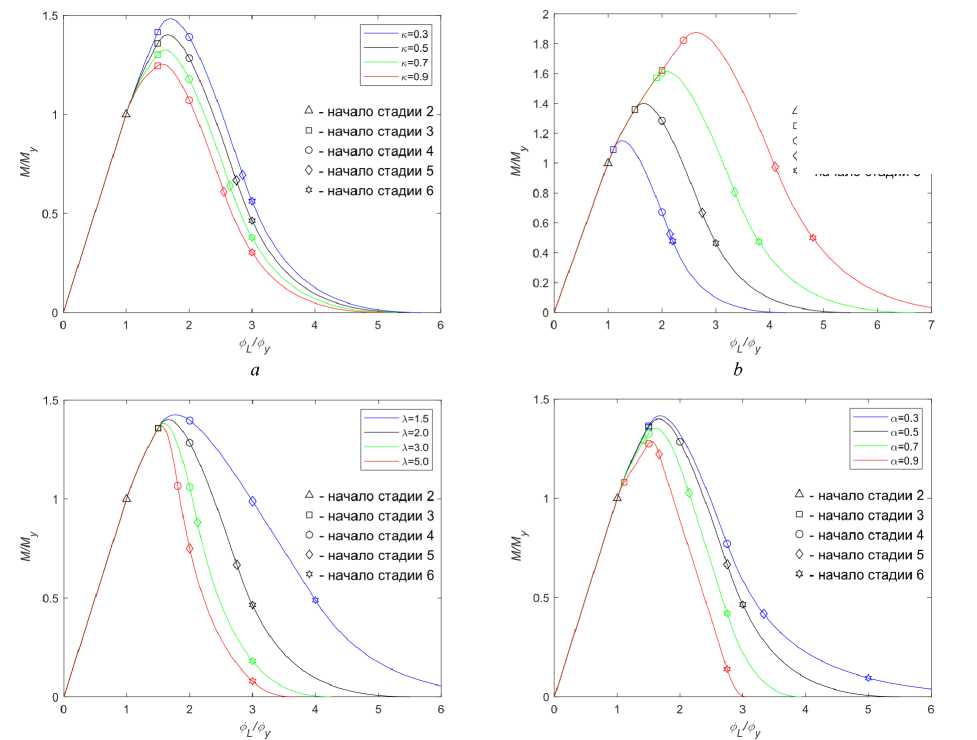
  Рис. 9. Диаграммы нагружения при различных значениях κ ( а ), β ( b ), λ ( c ) и α ( d )

  
  
  
  
  

Fig. 9. Loading diagrams for various values of κ ( а ), β ( b ), λ ( c ) and α ( d )

На рис. 9 приведены диаграммы нагружения в относительных координатах для различных наборов значений параметров κ , β , λ и α . Анализ показывает, что увеличение максимального значения крутящего момента происходит при росте модуля упрочнения, росте протяженности стадии упрочнения, снижении модуля спада и снижении внутреннего диаметра стержня. Рост максимального значения момента сопровождается смещением точки экстремума вправо, что говорит о сопутствующем увеличении деформационных резервов конструкции.

Анализ выражений (25г), (27б), (28г), (29б), (30б), (31б) позволяет сформировать условие реализации полной диаграммы нагружения при кручении полого цилиндрического тела:

1 -α ^{4 - 1,}

1 χ< ;

α

1 -α ⁴

- 1,¹ ≤χ< ^β ; (33) αα

λ - 1, ^β ≤χ . α

Заключение

В работе получено новое аналитическое решение краевой задачи механики закритического деформирования о кручении толстостенного цилиндрического тела с учетом жесткости нагружающей системы. Были рассмотрены двухзвенная и трехзвенная кусочно-линейная аппроксимации полной диаграммы деформирования материала. Получены и проанализированы соотношения, описывающие зависимость крутящего момента от угла поворота торца стержня на различных стадиях деформирования. Определены точки максимума и максимальные значения функции момента; выявлена их связь со свойствами материала и геометрией полого стержня. Выявлены значительные прочностные и деформационные резервы рассматриваемой конструкции. Рассмотрен вопрос устойчивости закритического деформирования при кручении. Определена необходимая для реализации полной диаграммы нагружения жесткость нагружающей системы. На основе вышеизложенного можно сделать вывод о рациональности и необходимости учета стадии разупрочнения материала и жесткости нагружающей системы в расчетах конструкций.