Устойчивые к атакам на контейнер стеганографические алгоритмы
Автор: Смагин Алексей Аркадьевич, Валишин Марат Фаритович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Электромагнитная совместимость и безопасность оборудования
Статья в выпуске: 1 т.13, 2015 года.
Бесплатный доступ
В статье рассматривается задача построения стеганографических алгоритмов, способных организовывать скрытый канал передачи данных в условиях проведения целенаправленной атаки на контейнер. Разработаны теоретические методы на основе редукции множества контейнеров и оценки вносимого в результате атаки искажения. Приведена практическая реализация стеганографического алгоритма, устойчивого к операции преобразования цветного изображения в оттенки серого и JPEG компрессии.
Стеганография, стегоанализ, активная атака, робастность, стеганографический алгоритм, цифровая обработка изображений, jpeg компрессия
Короткий адрес: https://sciup.org/140191747
IDR: 140191747
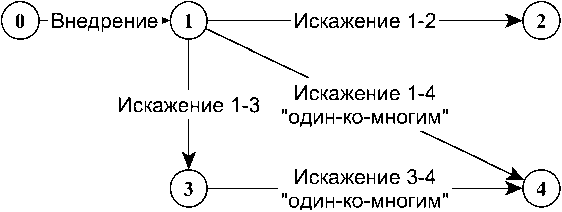
Список литературы Устойчивые к атакам на контейнер стеганографические алгоритмы
- Gustavus J. Simmons. The Prisoner’s Problem and the Subliminal Channel, Advances in Cryptology: Proceedings of Workshop on Communications Security (Crypto'83, David Chaum, ed.). Plenum Press. 1984. -P. 51-67.
- Конахович Г.Ф., Пузыренко А.Ю. Компьютерная стеганография. Теория и практика. К.: МК-Пресс, 2006. -288 с.
