Устройства для преобразования движения в структуре диады механической колебательной системы

Введение. Вопросы о расширении элементной базы механических колебательных систем давно привлекают внимание и неоднократно рассматривались с позиций возможности развития обобщенных подходов в системах многофункционального назначения, что нашло отражение в работах по структурному математическому моделированию [1-3]. В последние годы наметился интерес к детализации представлений о принципах динамических аналогий и формах их реализации в теории цепей и в различных приложениях. Интерпретации механических колебательных систем на основе аппарата теории автоматического управления рассмотрены в работах, ориентированных на решение задач динамического синтеза виброзащитных систем [4-6], что инициирует внимание к поиску и детализации представлений о взаимодействиях типовых элементов. В частности, интерес представляет рассмотрение диад как типовых фундаменто-образующих структур линейных механических колебательных систем. Вместе с тем диады, как структуры, обладающие двумя степенями свободы, могут, в свою очередь, содержать не только упругие и массоинерционные элементы обычного вида, но и типовые элементы, реализующие функции преобразования движения [1, 3, 5]. В настоящей работе рассматриваются особенности динамических свойств диад в линейных механических колебательных системах цепного типа, содержащих в своем составе устройства для преобразования движения.

• I.    Общие положения. Постановка задачи исследования. Рассмотрим механическую линейную колебательную систему с двумя степенями свободы, продемонстрированную на рис. 1. На систему действуют гармонические внешние силы Q 1 и Q ₂, приложенные непосредственно к массоинерционным элементам m 1 и m ₂. В системе имеются упругие элементы с жесткостями k 1 , k ₂, к ₃, а также устройство для преобразования движения с приведенной массой L [1, 5].

  

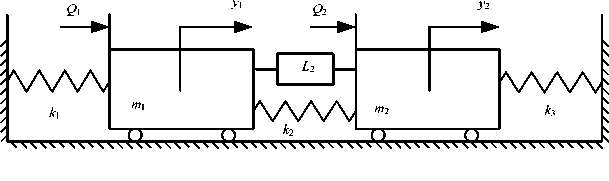
  Рис. 1. Принципиальная схема механической колебательной системы, содержащей диаду ( m 1 , к 2 , m 2 , L )

  
  

Fig. 1. Block diagram of mechanical oscillatory system containing dyad (m 1 , k 2 , m 2 , L)

Используя технологии структурного математического моделирования [3, 5], основанные на применении уравнений Лагранжа 2-го рода и последующих преобразований Лапласа, получим в качестве модели структурную схему эквивалентной в динамическом отношении системы автоматического управления (рис. 2).

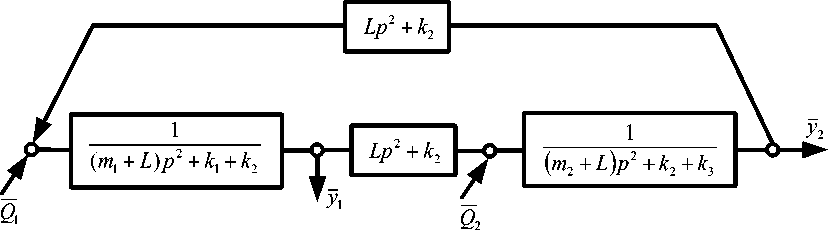
Рис. 2. Структурная схема системы с устройствами преобразования движения

Fig. 2. Structural diagram of system with motion translation devices

Рассматриваемая система обладает линейными свойствами и совершает малые колебания относительно положения статического равновесия. На рис. 2 приняты следующие обозначения: p = j и — комплексная переменная; значок <-> соответствует изображению переменной по Лапласу. Понятие о приведенной массе L устройства для преобразования движения более подробно рассматривается в [7]. Отметим, что устройство для преобразования движения (УПД) может быть реализовано в различных конструктивно-технических формах, например, в виде рычажных, зубчатых или винтовых несамотормозящихся механизмов.

Машиностроение и машиноведение

Используя структурную схему (рис. 2), можно получить передаточные функции исходной системы, полагая что y и у ₂ являются выходными сигналами, а внешние воздействия Q 1 , Q ₂ — входными. Принимая для упрощения, что Q 1 + 0 ( Q ₂ = 0), запишем передаточные функции:

где

W (_р) = y 1 = m 2 Р ^{2 + L} P ^{2 + k} 2 ^{+ k} 3 _;

Q i

W 2( Р ) = £ Q i

A ⁽ Р )

Lp ²+ k ₂ _ A ⁽ Р ) ’

A ( p ) = ( m 1 p ² + Lp ² + k 1 + k ₂)( m ₂ p ² + Lp ² + k ₂ + k ₃) - ( Lp ² + k ₂)²

— характеристическое частотное уравнение системы.

Кроме передаточных функций (1), (2) в рассмотрение вводится передаточная функция межпарциальных связей:

W 12 ( p ) =

У 2 =       Lp ^{2 +} k 2

y   m ₂ p ² + Lp ² + k ₂ + k ₃

В случае одновременного действия двух сил Q 1 и Q ₂ возможно использование принципа суперпозиции [8]. Отметим, что простые формы преобразований реализуются в случаях, когда обе внешние силы имеют одну частоту и действуют синхронно.

Задача исследования заключается в разработке метода оценки динамических свойств диады с устройством для преобразования движения и использования динамических эффектов для режима прикладных задач динамики вибрационных технологических машин.

• II.    Диада и ее динамические свойства. Диада рассматривается как структурное образование из типовых элементов с передаточными функциями инерционных звеньев m i , m ₂, упругого звена k ₂ и УПД. Отметим, что диада, как некоторое структурное образование, находится «в изоляции» от связей с опорными поверхностями ( k 1 = 0, k ₃ = 0). При этом не учитываются силы сопротивления со стороны опорной горизонтальной поверхности.

Структурная схема диады и некоторые формы её преобразований приведены на рис. 3, а , б , в .

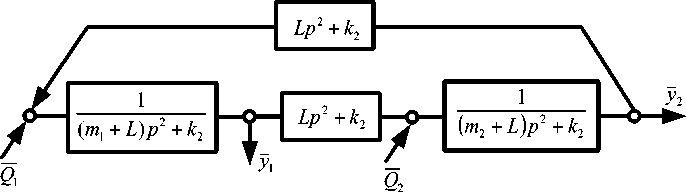
а)

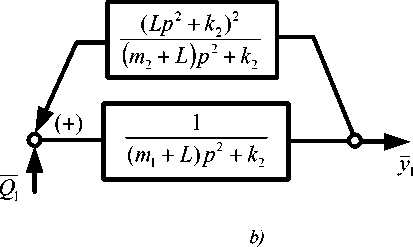
Рис. 3. Структурная схема диады: а) общий вид; b) структурная схема диады при исключении координат у ₂ ; с) структурная схема системы с выделением объекта вибрационной защиты m i

c)

Fig. 3. Dyad structural scheme: a) - general form; b) - dyad structure when excluding coordinates у ₂ ;

c) – system structural scheme with allocation of vibration protection object m 1

Передаточные функции диады на основе использования структурных схем (рис. 3, а, б, в ) принимают вид:

W„ ( p )- 11 - m ■ p ’ ⁺ Lp ‘ ⁺ k ■ ,                                         (5)

• ¹        Q 1        4( p )

  w .( p )= й- = k , 2         Q 1 A 1 ( p )	(6)
  W 2 д ( p ) =   =     Lp 2 + k 2 , ,	(7)
  Z m 2 p + Lp + k 2

  где	A1 ( p ) = ( m 1 p 2 + Lp 2 + k 2)( m 2 p 2 + Lp 2 + k 2) - ( Lp 2 + k 2)2                                  (8)

— характеристическое частотное уравнение диады.

Выражение (8) может быть упрощено и приведено к виду: p 4[ m 1 m 2 + L ( m 1 + m 2)] + p 2 k 2( m 1 + m 2) = 0 .                                        (9)

Из (9) следует, что система имеет циклическую координату. Это обеспечивает возможность рассмотрения диады в рамках прямолинейного поступательного перемещения как некоторого установившегося движения. При этом в соответствии с характеристическим уравнением будет верно равенство:

p ²{[ m 1 m ₂ + L ( m 1 + m ₂)] p ² + k ₂( m + m ₂)} = 0 . (10)

Из (9), (10) очевидно, что диада имеет одну частоту собственных колебаний ю2д = 0. Вторая частота соб- ственных колебаний диады определяется выражением:

₂         k ₂ ( m_x + m ₂)

^ю2 д =--------- 7", ---------7

m ₁ m ₂ + L ( m + m ₂)

.

Если считать, что диада имеет без УПД приведенную массу

mm ш = —1—2— mnp , , m + m 2

то с учетом (11) приведенная масса диады с УПД составит

m v тт = m + L . пр УПД пр

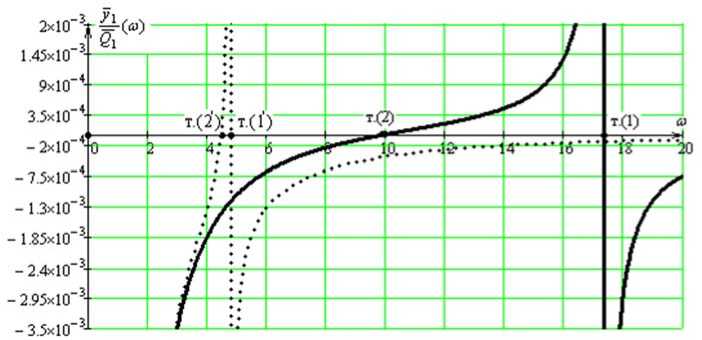
Введение УПД в диаду уменьшает частоту собственных колебаний и вид амплитудно-частотных характеристик (АЧХ) системы. На рис. 4, а , б приведены для сравнения АЧХ обычного вида и АЧХ с введенными УПД.

а )

Машиностроение и машиноведение

b )

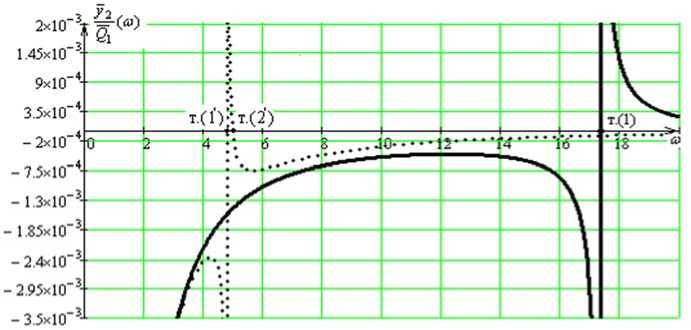
Рис. 4. Амплитудно-частотные характеристики диады: а — АЧХ по координате y 1 ; b — АЧХ по координате y 2 (     — при L = 0,

— при L = 80 кг)

Fig. 4. Dyad amplitude-frequency characteristics: а – AFC in coordinate y 1 ; b – AFC in coordinate y 2 (      – at L = 0,

– at L = 80 kg )

Для модельной задачи принято, что m1 = 10 кг, m2 = 20 кг, k2 = 2000 Н/м; приведенная масса L принимает два y значения — L = 0 и L = 80 кг. Графики амплитудно-частотных характеристик ^-(ю) при L = 0 и L = 80 кг имеют от-Q1

личия. Частоты собственных колебаний определяются положением точек (1) и (1') на оси абсцисс. При увеличении L y значение частоты собственных колебаний уменьшается. При L = 0 график ^-(ю) пересекается с осью абсцисс в точке Q1

• (2) . При увеличении L эта точка перемещается в точку (2') (рис. 4, а ). Характерно, что при увеличении L значения частоты динамического гашения колебаний и частоты собственных колебаний сближаются.

y

Графики АЧХ — (ю) (рис. 4, б) при L = 0 и L = 80 кг имеют характерные точки (1) и (1) на оси абсцисс, опре- Q 1

деляющие значения частот собственных колебаний. При L = 0 график y²- (ю) не имеет пересечений с осью абсцисс.

Q 1

Вместе с тем график y ² (ю) при L = 80 кг имеет пересечение с осью абсцисс в точке (2'), что свидетельствует о воз- Q 1

никновении режима динамического гашения колебаний. Таким образом, параметр УПД, называемый приведенной массой L , может существенно изменять свойства диады и влиять на особенности движений системы в целом.

Отметим также, что точка (2') на рис. 4, б находится правее точки (1'), что свидетельствует о наличии особых режимов динамического взаимодействия элементов диады. Для диады без УПД АЧХ имеют вид, характерный для систем с одной степенью свободы. При этом полагается, что циклическое движение может на данном этапе исследования не рассматриваться.

С учетом УПД движение по координате y ₁ имеет частоту динамического гашения:

2          k 2

^ю 1 дин _г m ₂ + L

При этом частота собственных колебаний определяется выражением:

ю2 .. =-----k2 со6д Т mm L + —

m 1 + m ₂

При частоте возмущения ю ^ ж , система «запирается» и W 1_g ( p ) стремится к значению

m2 + L

Wig ⁽ р ) =                 ;

р ^« m 1 m ₂ + L ( m 1 + m ₂)

По координате y ₂ режим динамического гашения колебаний определится выражением:

2       k 2

^ю 2 дин l ;

соответственно на высоких частотах получим:

W2 д(p) = p ^a>

L

m 1 m 2 + L ( m 1 + m 2 )

.

Таким образом, введение УПД привносит в диаду новые динамические эффекты. В частности, возможным становится динамическое гашение колебаний по координате y 2 (17), изменяются также значения парциальных частот диады и ее собственной частоты.

Передаточная функция межпарциальных связей с учетом УПД имеет вид, определяемый выражением (7), из которого следуют особенности динамических взаимодействий в межкоординатных связях y1 и y2 . Характерным является «обнуление» (7) или ситуация, когда y2 = 0, что не является возможным в диадах без устройств для преобразо- вания движения. При p ^ 0, соотношения амплитуд y^ = 1, а при p ^ да , y2 =

y ₁

y ₁

L

, что можно рассматривать как m ₂ + L

форму проявления рычажных связей [9, 10].

Одновременное действие двух внешних силовых факторов не изменяет характеристическое частотное уравнение диады, но влияет на формы передаточных функций. Примем, что Q2 = aQ1, тогда wg (p) = y2

Q ₁

W^ g ( p ) = y ²

Q ₁

( m 2 + L ) p ² + k ₂ + a( Lp ² + k ₂)

A ( p )

[( m 1 + L ) p ² + k ₂]a + Lp ² + k ₂

;

W д ( p ) = y ²

y ₁

A ( p )

[( mm + L ) p ² + k ₂]a + Lp ² + k ₂ ( m ₂ + L ) p ² + k ₂ +a( Lp ² + k ₂)

;

.

При действии двух силовых факторов частоты собственных колебаний не изменяются. При этом изменяются частоты динамического гашения колебаний. По координате y 1 имеем:

^Ю 1 динд

k ₂ (1 + a ) m ₂ + L (1 + a )

.

По координате y 2 соответственно получим:

® 2динд =

k ₂ (1 + a )

a m 1 + L (1 + a )

.

Отметим, что одновременное действие двух силовых факторов без сдвига по фазе можно рассматривать как способ изменения параметров приведенной жесткости системы, а также как способ изменения приведенных масс системы.

Для случая ^_Хдинд = су _динд можно получить следующее уравнение связности:

k ₂ (1 + a )

k ₂ (1 + a )

m 2 + L (1 + a )   a m 1 + L (1 + a)’

откуда следует, что

m a = — m1

.

m

Если выполняется условие a = —-, то в системе реализуется особый динамический m ₁

режим, при котором

y

^- = 1, что соответствует движению объекта по двум координатам как «единое целое», то есть имеет место синфаз- y ₁

ное движение с одинаковыми амплитудами. Аналогичным образом могут быть получены и другие формы движений.

III. Использование энергетической функции. Если рассматривать диаду с УПД, то в системе координат y 1 , y 2 её кинетическая и потенциальная энергии определяются выражениями:

T = ;2 m 1 y 12 + 2 m 2 y 22 + J- L ⁽ y 1 - y ₂)² ,

^П = 2 ^k 2 ⁽ У 2 - y 1 ) .

Частотная энергетическая функция может быть записана в виде:

Машиностроение и машиноведение

тогда

____________ k 2 ⁽ У 2 ^— У 1 )² _____________

⁽ m i + L ) ^у2 + ⁽ m 2 + L ) y ^{2 - 2} Ly i y 2 '

Введем понятие коэффициента связности координат:

i = У 2/ У 1 ,

(28')

_ю 2 =        k 2 ( i - 1)²

m₁ + m ₂ i ² + L ( i - i)²

Рассмотрим, как влияет L на коэффициент формы связи координат i. Если УПД нет, то L = 0, а (29) примет вид:

₁2 = k 2 ( i — i)² m i + m 2 i ²

Сравнивая с частотой собственных колебаний, определенной выше, получим: k ₂( i - 1)² =     к ₂

m1 + m 2 i2     m1 m 2 ’ m1 + m 2

откуда следует, что i =

m 1

m ₂

Если в диаду ввести УПД, то (31) трансформируется к виду: k 2 ( i - 1)²        =       k 2

m 1 + m 2 i + L ( i — 1)     l + ^m 1 ^m 2

m ₁ + m ₂

откуда найдем, что значение i не зависит от L

i =

m 1

m ₂

На рис. 5 приведены результаты решения уравнения (29) по определению значений коэффициента связности i при различных значениях L (в модельной задаче приняты: m 1 = 10 кг, m 2 = 20 кг, k 2 = 2000 Н/м, L = 0, 10, 20, 50 кг).

^(0;

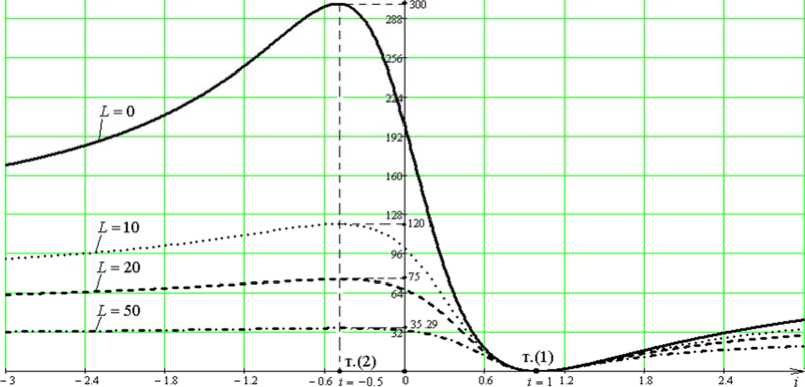
Рис. 5. Графики зависимости m ² ( i ) при различных значениях L

Fig. 5. Dependency graphs m ² ( i ) at different values of L

Из графиков на рис. 5 очевидно, что динамическое состояние диады не может находиться в форме колебаний, когда i = 1, поэтому все графики m2(i) при различных значениях L пересекаются в одной точке (1) на оси абсцисс (i = 1); при этом т2об = 0 при всех значениях L. В данном случае это означает, что система имеет циклическую координату, характеризующую установившееся равномерное прямолинейное движение. Вместе с тем все графики с различными значениями L имеют экстремальные свойства при i = -0.5, что следует из выражения (34). Таким образом, учет L (приведенная масса УПД) не приводит к изменению связности координат i, но при этом изменяются соответствующим образом значения частот собственных колебаний диады. При увеличении L частоты собственных колебаний диады уменьшаются (в пределе до нулевых значений), что связано с представлениями о получении очень низких частот при L → ∞.

При i = 0, что соответствует — = 1, частоты собственных колебаний определяются вышеприведенным выра- y ₁

жением (29). При i → +∞ из (29) следует, что

• 2    = к.. ^ω

  .

  
  
  
  

1 >■/ m 2

k

Отметим, что графики на рис. 5 при i → – ∞ будут также стремиться к пределу 2 , определяемому выра-m 2 + L жением (35), что соответствует парциальной частоте системы, состоящей из элементов m2, k2 и L.

Амплитудно-частотные характеристики (АЧХ) диады при внешнем силовом возмущении к элементу m 1 приведены на рис. 6, а , б , в , г , где значение приведенной массы L изменяется в пределах L = 0 (рис. 6, а ); L = 10 кг (рис. 6, б ); L = 20 кг (рис. 6, в ); L = 50 кг (рис. 6, г ).

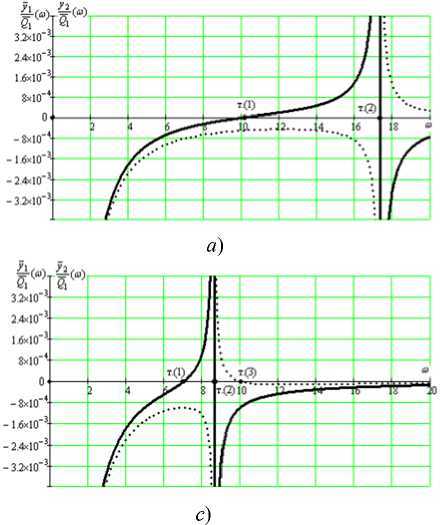
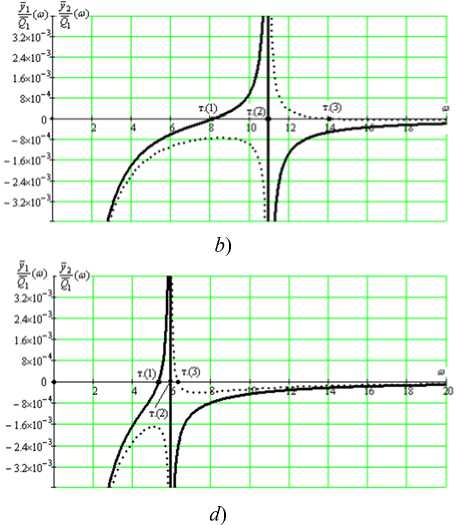
Рис. 6. Формы амплитудно-частотных характеристик диады при различных значениях приведенной массы устройства для преобразования движения L : а ) L = 0; b) L = 10 кг; c) L = 20 кг; d) L = 50 кг

(сплошная линия (     ) соответствует графику зависимости по координате y ₁ ;

точечная линия (       ) соответствует по координате y ₂ )

Fig. 6. Forms of dyad amplitude-frequency characteristics at different values of reduced mass of motion translation device L: а – L = 0; b – L = 10 kg ; c – L = 20 kg ; d – L = 50 kg (solid line ( ) corresponds to dependency graph in coordinate y ₁ ;

dotted line (        ) corresponds to the one in coordinate y ₂ )

АЧХ на рис. 6, а отображают динамические свойства без УПД при значениях параметров m1 = 10 кг, m2 = 20 кг, k2 = 2000 Н/м. В рассматриваемом случае система имеет одну частоту собственных колебаний (ω2 ≠ 0), которая определяется точкой (2) на оси частот. В движениях по координате y1 реализуется режим динамического гашения колебаний точки (1) на оси частот. Движение по координате y2 происходит без режима динамического гашения y колебаний, но АЧХ по координате y1 имеет характерную форму с наличием минимального значения 1 .

Q 1

Введение УПД с приведенными массами L = 0, 10, 20, 50 кг, что отображается на АЧХ, приведенных на рис. 6, приводит к появлению ряда новых динамических эффектов. Это связано с проявлениями режимов динамического гашения колебаний по координате y 1 . При этом значение частоты собственных колебаний ω 2 ≠ 0 сдвигается в область более низких значений (точка (1) на рис. 6). На графиках АЧХ при L ≠ 0 , частоты динамического гашения ко-

Машиностроение и машиноведение

лебаний (т. (3) на рис. 6, б , в , г ) сдвигаются в сторону расположения точки (2), определяющей частоту собственных колебаний. Отметим, что сближение частот динамического гашения колебаний и собственных колебаний не является приемлемым для решения ряда задач динамики из-за возможностей проявления свойств, характерных для форм неустойчивых движений [11].

IV. Возможности физической реализации диады с использованием рычажных механизмов. Рассмотрим пример реализации диады в структуре динамического корректора колебаний в виброзащитной системе с двумя степенями свободы. На рис. 7 рассматривается механическая колебательная система с двумя степенями свободы как расчетная схема некоторого технического объекта массой m 2 , который опирается на УПД рычажного типа. Такое устройство является стержнем, на одном конце которого размещен груз массой m 0 с возможностями изменения расстояния l 2 до точки вращения (точка В). В точке А (рис. 7) рычаг имеет связь в виде кинематической пары V класса (вращательная) с объектом защиты (АВ = l 1 ). Одновременно в точке В рычаг соединяется вращательной кинематической парой с промежуточной массой m 1 . В системе используются четыре упругих элемента с жесткостями k 1 , k 2 , k 3 и k 4 (рис. 7). Движение системы описывается в системе координат y 0 , y 1 , y 2 , связанной с неподвижным базисом; при этом положению объекта защиты m 2 соответствует координата y 2 , положению рычага — y 0 , промежуточной массы — y 1 . В качестве внешнего возмущения рассматриваются гармонические колебания опорной поверхности z ( t ). Система обладает линейными свойствами и совершает малые колебания относительно положения устойчивого статического равновесия.

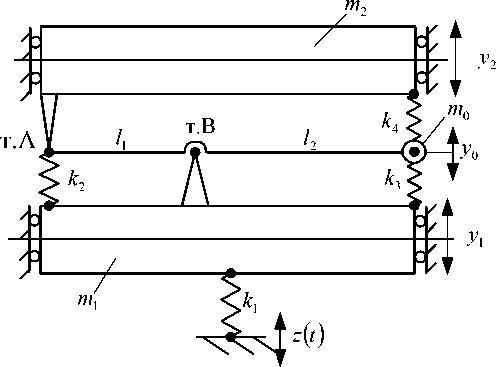
Рис. 7. Принципиальная схема виброзащитной системы технического объекта с УПД

Fig. 7. Block diagram of vibration protection system of technical object with motion translation device

В системе координат y 1 и y 2 выражения для кинетической и потенциальной энергий имеют вид: 1 ₂ 1 ₂ 1 ₂

T = 2 m l У 1 + 2 m 2 y 2 + 2 m _o y _o,

П = 2 k i ( У 1 - z ) ² + 2 k 2 ( у 2 - У 1 ) ² + 2 k з ( у o - У 1 ) ² + 2 k 4 ( у 2 - у 0 ) ².

С учетом кинематических соотношений сложного движения (36), (37) и введением коэффициента рычажной l связи i = — получим:

l 1

T = 2 m l y² + 2 m 2 y ^ + 2 m 0 [ ^y ( 1 + i p ) - ^y 2 i p ] ²,

^П = ^ ^k 1 ( y i - z ) ^{2 +} 2 k 2 ⁽ У 2 - y i )^{2 +} 2 k 3 i p ( y i - y 2 ⁾² + 2 k 4 ⁽¹ + i p ⁾² • ⁽ y 2 - y i )².

В данном случае уравнения движения системы принимают вид:

^y i I m i ⁺ m 0 ( i p ⁺ 1 ) ² 1 + y i

k i + k 2 + k 3 i p + ^{+ k} 4 ( i p ^{+ i} )

- ^y 2 m 0 i p ( i p ^{+ i} ) - у 2

k 2 + k 3 i p +

+ k 4 ( ⁱ + i p )

= k i z ( t ),

^y 2 ( m 2 ⁺ m 0 i p ) ⁺ У 2

^k 2 ^{+ k} 3 i p ⁺

+k4 (i + ip )

^{- y} i m 0 i p ( i p ^{+ 1} ) ^- y i

k 2 + k 3 i p +

+ ^k 4 ( ^{i +} i p )

= 0.

На основании дифференциальных уравнений (40), (41) после преобразований Лапласа [3, 5] может быть построена структурная схема (рис. 8), которая имеет две координаты y1 и y2 . Что касается координаты y0 , то она свя- зана с y1 и y2 следующими соотношениями:

y 0 = У 1 ( 1 + i p ) - y 2 i p .                                                          ⁽⁴²⁾

Коэффициенты уравнений (40) и (41) в операторной форме приводятся в таблице 1.

Таблица 1

Table 1

Коэффициенты уравнений (40), (41) в координатах y ₁ , y ₂

Coefficients of equations (40), (41) in coordinates y 1 , y ₂

а 11	а 12
m l + m 0 ( i p + 1 ) 2 p 2 + k 1 + k 2 + k 3 i 2 + k 4 ( i p + 1 ) 2	- [ m 0 i p ( i p + 1 ) P 2 + k 2 + k 3 i p + k 4 ( 1 + i p ) ]
а 21	a 22
- [ m 0 i p ( i p + 1 ) p 2 + k 2 + k 3 i 2p + k 4 ( 1 + i p ) 2 ]	( m 2 + m 0 i p ) p 2 + k 2 + k 3 i p ' + k 4 ( 1 + i p ) 2
Q 1	Q 2
k 1 z ( t )	0

Примечание: p = j и — комплексная переменная ( j = V-l ); символ <-> над переменной означает её изображение по

Лапласу [3, 5].

Структурная схема системы в соответствии с данными таблицы 1 имеет вид, проиллюстрированный на рис. 8. При частоте

2 k 2 + k з i p + k 4 ( 1 + i p ) ® меж =          . /.

m0ip (ip + 1)

межпарциальная связь «обнуляется» и система принимает вырожденную форму. В общем случае по каждой из координат возможны режимы динамического гашения колебаний на частотах

1дин

^k 2 + к з 1 2 + k 4 ( 1 + i _p ) 2

=                   . . 2            , m 2 + m о ip

2 дин

^k 2 ^{+ k} 3 i P ^{+ k} 4 ( 1 ⁺ i p ) m 0 i p ( i p ⁺ 1 )

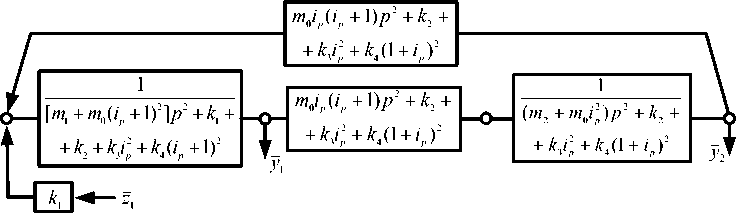
Рис. 8. Структурная математическая модель механической колебательной системы, изображенной на рис. 7

Fig. 8. Structural mathematical model of mechanical oscillatory system pictured in Fig. 7

Передаточные функции системы при кинематическом возмущении определяются из структурной схемы и

имеют вид:

y     ⁽ m 2 + m 0 i p ) p 2 + ^k 2 + ^k з i p + ^k 4 ⁽¹ + i p ) 2

W( p) = =----------—--------- k1z1                     A(p)

Машиностроение и машиноведение

wr x   У 2     m 0 i p ⁽ i p ^{+ 1)} P^{1 +} k 2 + k 3 i P ⁺ k 4 ⁽¹ + i p ⁾²

W2(p) = —— = —-----------------— k1 z1                     A(p)

Введем понятие передаточной функции межпарциальных связей:

У   m 0 i p ⁽ i p ^{+ 1)} P ^{2 + k} 2 ^{+ k} 3 i P ^{+ k} 4 ^{(1 +} i p ⁾²

W ₂( P ) =   =₂₂ 2 ^,

У 1   ⁽ m 2 ⁺ m 0 i p ) p ^{+ k} 2 ^{+ k} 3 i p ^{+ k} 4 ^{(1 +} i p )

где

A ⁽ P ) = {[ m i ⁺ m 0 ⁽ i p ^{+ 1)2} ] P ^{2 + k} i ^{+ k} 2 ^{+ k} 3 i p ^{+ k} 4 ⁽ i p ^{+ 1)2} x x [(} m 2 + m 0 i 2 ) p ² + к 2 + к 3 i p + к 4 ⁽¹ + i p ^{)2 ] - [} m 0 i p ⁽ i p + 1) p ² + к 2 + к 3 i p + к 4 ⁽¹ + i p ^{)2 ]2}

— характеристическое частотное уравнение системы.

Если i р = 0, то выражения (46), (47) трансформируются к виду:

W ( P ) =

У 1 ^k 1 z

m ₂ p ² + k ₂ + k ₄

A ( P

W 2 ( p ) =

У 2 ^k 1 Z

k ₂ + k ₄

A ' ( p ) ,

где

A ' ( P ) = [( m₁ + m 0 ) P ² + ^k ₁ + ^k 2 + ^k 4 ] ' ( ^m ₂ P ² + k ₂ + k ₄) - ( k ₂ + k ₄) 2

— характеристическое частотное уравнение исходной системы при i_p = 0.

Парциальные частоты системы в общем случае определяются выражениями:

2 k1 + k2 + k3i2 + k4 (Ip + 1)2 П =--------------------2-----, m1 + m 0( ip +1)

2 k 2 + k 3 i> k 4 (1 + i p )² n 2 = ---------------^------- .

m ₂ + m ₀ i_P

При k 1 = 0 структурная схема на рис. 8 преобразуется в структурную схему диады, приведенную на рис. 9.

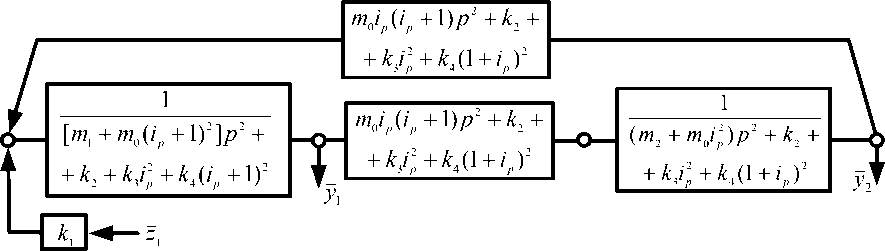
Рис. 9. Структурная схема диады в общем виде

Fig. 9. Dyad structural diagram in general form

Переход к унифицированной форме диады осуществляется на основе формальных приемов, которые заключаются в выделении для передаточных функций парциальных систем фрагментов, имеющих вид передаточных функций межпарциальных связей. Таким образом, по координате у , справедливо выражение:

^[ m 1 ⁺ m 0 ⁽ i p ^{+ 1)2 ]} P ^{2 + k} 2 ^{+ k} 3 i ^{2 + k} 4 ⁽ i p ^{+ 1)2} = m 1 P ^{2 +} m 0 ⁽ i p ⁺ !) P ^{2 +} m 0 i p ⁽ i p ^{+ 1)} P ^{2 + k} 0 = = ^[ m 1 + m 0 ⁽ i p + ^1)] p ² + m 0 i p ⁽ i p + 1) p ² + k 0 = ^[ m 1 + m 0 ⁽ i p + ^1)] p ² + Lp ² + k 0 .

В свою очередь, по координате у ₂ получаем равенство:

⁽ m 2 + m 0 i p ) p ² + k 2 + k 3 i p + k 4 ⁽¹ + i p ⁾² = ⁽ m 2 ^- m 0 i p ) p ² + m 0 i p ⁽ i p + 1) p ² + k 0 = = ⁽ m 2 ^- m 0 i p ) p ² + Lp ² + k 0 .

Структурная схема (рис. 9) на основе выражений (55), (56) преобразуется к виду, изображенному на рис. 10.

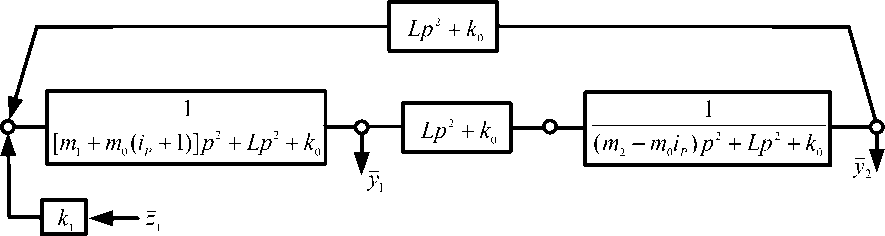
Рис. 10. Структурная схема диады с устройством для преобразования движения

Fig. 10. Dyad structural diagram with motion translation device

Таким образом, в составе расчетной схемы в виде механической колебательной системы с двумя степенями свободы (рис. 7), имеющей рычажный механизм второго рода может быть выделена диада. В диаде кроме обычных массоинерционных элементов m ‘ = m 1 + m 0 ( i p + 1) и m ‘ = m ₂ - m 0 i p содержится УПД с передаточной функцией

L = m о i p ( i p + 1),                                                         (57)

а также обобщенная пружина с коэффициентом жесткости k 0 , который соответствует жесткости трех параллельно соединенных пружин:

k ₀ = k ₂ + k з i p + k 4 ( i_p + 1)².                                                   (58)

При «обнулении» k 2 , k 3 , k 4 и m 0 система превращается в обычную диаду, рассмотренную в предыдущих разделах статьи.

Заключение. Диада в механических колебательных системах представляет собой структурное образование, которое в составе механических колебательных систем может рассматриваться как системообразующий элемент, предопределяющий динамические свойства системы в целом.

Доказано, что диада может быть выделена из исходной системы и представлена в условиях изоляции от связей с внешними элементами и опорными поверхностями, либо рассматриваться во взаимодействиях с такими поверхностями без учета сил сопротивления. В рамках такого подхода диада представляет собой систему с двумя степенями свободы, в которой соединение массоинерционных элементов происходит через линейную пружину.

Авторами развиты и детализированы представления о динамических свойствах диад, включающих в свой состав дополнительные связи, введенные параллельно упругому элементу, реализуемые в виде устройств для преобразования движения. Представлены структурные математические модели в динамическом отношении эквивалентные структурным схемам систем автоматического управления. Усилительное звено рассматривалось как эквивалент пружины, а звено УПД — как типовое звено структурной модели, имеющее передаточную функцию дифференцирующего элемента второго порядка.

Введение такого рода связей в структуру диады существенным образом изменило набор её динамических свойств по сравнению с обычными подходами. Показано, что устройство для преобразования движения с передаточной функцией дифференцирующего звена второго порядка может быть практически реализовано с использованием рычажных механизмов.

Таким образом, предложен метод построения математической модели диады общего вида: произведена оценка динамических свойств диад, выявлены новые динамические эффекты, отражающие возможности учета особенностей форм движения элементов диады и совместного действия внешних сил, что создает возможности для поиска и разработки новых подходов в управлении динамическим состоянием механических колебательных систем.