Устройство на основе ПЛИС для распознавания рукописных цифр на изображениях
Автор: Зоев Иван Владимирович, Береснев Алексей Павлович, Марков Николай Григорьевич, Мальчуков Андрей Николаевич
Журнал: Компьютерная оптика @computer-optics
Рубрика: Обработка изображений, распознавание образов
Статья в выпуске: 6 т.41, 2017 года.
Бесплатный доступ
Рассмотрена задача создания мобильного и энергоэффективного устройства, позволяющего распознавать рукописные цифры на изображениях с помощью свёрточных нейронных сетей. Устройство реализовано на основе программируемой логической интегральной схемы, входящей в систему на кристалле Cyclone V SX. При этом разработаны функциональные схемы вычислительных блоков, реализующих процедуры свёртки и подвыборки, а также функциональная схема самой свёрточной нейронной сети предложенной архитектуры. Приведены результаты исследования эффективности созданного устройства на программируемой логической интегральной схеме в части точности распознавания рукописных цифр, производительности устройства и его энергопотребления. Показаны результаты сравнения эффективности аппаратной реализации свёрточной нейронной сети с её программной реализацией.
Распознавание рукописных цифр на изображениях, свёрточные нейронные сети, устройство на основе программируемой логической интегральной схемы
Короткий адрес: https://sciup.org/140228691
IDR: 140228691 | DOI: 10.18287/2412-6179-2017-41-6-938-949
Текст научной статьи Устройство на основе ПЛИС для распознавания рукописных цифр на изображениях
Распознавание образов (объектов) на изображениях включает в себя широкий круг задач, например, распознавание символов, в частности рукописных цифр, распознавание лиц, объектов различной физической природы. Методы и алгоритмы распознавания объектов на изображениях широко применяются при создании устройств компьютерного зрения в робототехнических комплексах различного назначения, при анализе аэрокосмических снимков и т.д.
Для распознавания объектов на изображениях весьма часто используются искусственные нейронные сети (ИНС) [1]. Наиболее эффективными из них для решения таких задач являются свёрточные нейронные сети (СНС) [2, 3].
Сегодня при решении ряда прикладных задач востребованы мобильные, малогабаритные и имеющие низкое энергопотребление устройства распознавания рукописных цифр на основе аппаратно реализованных СНС. При этом, учитывая высокую вычислительную сложность СНС, разработчикам приходится искать баланс между точностью распознавания цифр, производительностью и энергопотреблением таких устройств.
В данной статье описывается разработанное на основе программируемой логической интегральной схемы (ПЛИС) устройство, позволяющее распознавать рукописные цифры с помощью СНС предложенной авторами архитектуры, основанной на архитектуре LeNet5 [4]. Приводятся результаты исследования эффективности этого устройства в части точности распознавания цифр, его производительности и энергопотребления.
фикации, позволяющие отнести образы на изображениях (объекты) к определенному классу по существующим признакам, характеризующим такие объекты. Распознавание рукописных цифр – это частный случай задачи распознавания образов, который в настоящее время достаточно хорошо исследован [4, 5]. Сегодня при решении задачи распознавания рукописных цифр в качестве методов классификации используются весьма сложные, но и более точные методы, например, опорных векторов [6], и различного рода ИНС [7, 8]. Ряд исследователей вообще считает, что использование ИНС является наиболее перспективным направлением при распознавании на изображениях рукописных символов, в том числе цифр [9, 10]. Результаты многих исследований показывают, что точность классификации (точность распознавания символов) зависит от характера обучения ИНС, от объемов используемых обучающих выборок и т.д. [11–14].
Ян ЛеКун (англ. Yann LeCun) с коллегами для решения задачи распознавания рукописных цифр предложили новый вид ИНС – свёрточные нейронные сети [4]. Архитектура СНС, описанная в этой работе, получила название LeNet5. В [4, 15, 16] показано, что СНС по сравнению с ИНС других видов дают значительно меньшую ошибку при распознавании рукописных цифр.
В настоящее время при решении многих прикладных задач в области компьютерного зрения весьма востребованы мобильные, малогабаритные и имеющие низкое энергопотребление устройства распознавания рукописных цифр. Целью данной работы является создание такого устройства, аппаратно реализующего СНС предложенной архитектуры и обладающего высоким быстродействием и максимально возможной точностью распознавания рукописных цифр. При его разработке необходимо искать баланс между точностью распознавания рукописных цифр, энергопотреблением и быстродействием мобильного устройства из-за ограниченности используемых вычислительных ресурсов. Это потребует дополнительных исследований эффективности разрабатываемого устройства.
Для аппаратной реализации СНС, обладающих высокой вычислительной сложностью, необходима соответствующая элементная база, которая позволила бы создать устройство с высокой производительностью. Основными вычислительными устройствами, с помощью которых обычно реализуют ИНС, в том числе и СНС – центральные процессоры (CPU) компьютеров и графические процессоры (GPU). Однако такие процессоры имеют большое энергопотребление, что неприемлемо в нашем случае. Программируемые логические интегральные схемы (ПЛИС) имеют низкое энергопотребление, а также позволяют реализовать параллельные вычисления, что важно при удовлетворении требования к устройству по быстродействию. Исходя из этого, для аппаратной реализации СНС была выбрана система на кристалле Cyclone V SX, в которой, кроме ПЛИС, имеется двухъядерный процессор ARM Cortex – A9. Плата Terasic SoCkit [17], взятая за основу устройства, содержит выбранную систему на кристалле, ОЗУ ёмкостью 1 ГБ и слот для карты памяти MircoSD, которые напрямую подключены к процессору. Всё это позволяет упростить взаимодействие разрабатываемого устройства с подключаемыми периферийными устройствами и добиться от него низкого энергопотребления.
Отметим, что идея аппаратной реализации СНС на ПЛИС, по-видимому, впервые сформулирована в [18]. В работах [19, 20] показаны результаты ускорения вычислений при реализации СНС весьма сложной архитектуры AlexNet на ПЛИС с большими вычислительными ресурсами и с большим энергопотреблением. Такая ПЛИС позиционируется компанией Xilinx как основа для создания высокопроизводительных вычислительных систем. По количеству логических ячеек она превосходит выбранную нами ПЛИС в 11,7 раза, а по рабочей частоте — в 2 раза. Авторами этих работ не ставилась и не может быть решена с использованием такой ПЛИС задача по созданию мобильных устройств с низким энергопотреблением для распознавания рукописных цифр. Более того, исследуемые в [19, 20] методы распараллеливания вычислений для архитектуры СНС AlexNet не могут быть реализованы на ПЛИС, включая выбранную нами, с меньшими ресурсами. Предлагаемая и описанная далее архитектура СНС и её аппаратная реализация разрабатывались с учетом значительной ограниченности вычислительных ресурсов широко распространенных ПЛИС.
-
2. Архитектура свёрточной нейронной сети
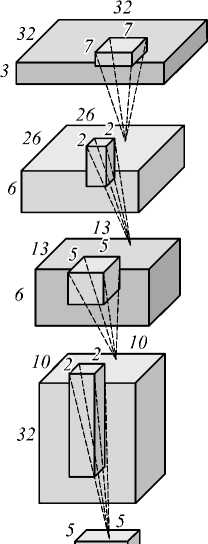
В предложенной нами архитектуре СНС (рис. 1), подобной архитектуре LeNet5, используются свёрточные слои (convolutional layers), слои подвыборки (pooling layers), а в качестве функции активации применяется оператор «выпрямитель» (англ. Rectified
Linear Unit – ReLU), название по аналогии с однопо- лупериодным выпрямителем в электротехнике.
Свёрточный слои:
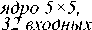
карты, шаг 1
Свёрточный слои: ядро 7x7, 3 входных карты, шаг 1
Слой подвыборки: окно 2 х?, шаг 2
Свёрточный слои: ядро 5x5, б входных карт, шаг 1
Слой подвыборки: окно 2x2, шаг 2
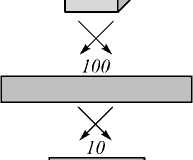
Полносвязный слой: выходов 10
Рис. 1. Архитектура СНС
Использование ReLU имеет по сравнению с другими функциями активации ряд преимуществ: не требует ресурсоёмких операций, таких как возведение в степень и т.п., и повышает скорость обучения сети [21]. ReLU заменяет все отрицательные элементы на нулевые. Данная функция активации вычисляется как max(0, x ).
Суть процедуры свёртки заключается в том, что каждый элемент двумерного изображения I умножается на матрицу K – ядро свёртки (англ. convolution kernel) размерности h×w поэлементно и результат суммируется и записывается в аналогичную позицию выходного изображения:
wh
( I * K ) xy = ЕЕ K j * I x + i , y + j , i = 1 j = 1
где x , y – координаты элемента в исходном изображении, i , j – координаты элемента в ядре свёртки, а w, h – ширина и высота ядра свёртки соответственно. Элементы изображения I являются входными значениями для нейрона в СНС, а ядро свёртки K хранит в себе значения весовых коэффициентов нейрона.
Ядро свёртки K по сути является фильтром, в котором закодирован некоторый ключевой признак объекта, извлекаемый из изображения. Таким образом, результат операции свёртки – это изображение, элементы которого хранят степень похожести фрагмента изображения на фильтр. Такое выходное изображение называется картой признаков.
Процедура свёртки является базовой для свёрточного слоя. Свёрточный слой содержит множество ядер свёртки, с помощью которых извлекаются ключевые признаки из входного изображения. В контексте метода СНС входным изображением свёрточного слоя является выход предыдущего слоя, к выходному слою применяется функция активации, а результаты записываются в карту признаков.
Архитектура свёрточного слоя задается параметрами: глубина – количество входных/выходных карт признаков; высота h и ширина w каждого из ядер свёртки; шаг, с которым ядро свёртки двигается по входному слою. Hа рис. 1 изображены 3 свёрточных слоя. Первый из них обладает следующими параметрами: высота и ширина каждого ядра равны 7 элементам, шаг равен 1 элементу, глубина равна 3 (три входные карты). Наличие трех входных карт признаков у первого слоя позволяет применять сеть предложенной архитектуры не только для распознавания рукописных цифр, но и других объектов на изображениях. В большинстве СНС конечные слои являются полносвязными. Можно задать параметры для свёрточного слоя таким образом, чтобы получить из него полносвязный слой. Так, полносвязный слой на рис. 1 можно представить как свёрточный слой с такими параметрами: высота и ширина ядра свёртки будут равны 1, входные карты признаков будут размером 1×1, а их глубина равна 100, количество выходных карт признаков будет равным 10.
Подвыборка (также может называться «пуллинг» от англ. pooling ) уменьшает размерность каждой карты признаков, но сохраняет наиболее значимую информацию. Из рис. 1 видно, что после первого свёрточного слоя, результатом которого является 6 карт признаков размером 26×26 элементов, идёт слой подвыборки с окном 2×2 элемента и шагом 2. Входная карта признаков при подвыборке разбивается на области размером 2×2 элемента. Для каждой такой области выполняется процедура подвыборки, которая может проводиться по разным алгоритмам, например, выбор максимальных значений элементов, среднее значение для элементов области, сумма значений элементов и т.д. После процедуры подвыборки получается 6 карт признаков размером 13×13 элементов.
В случае подвыборки с использованием максимальных значений элементов (англ. max pooling) в выходное изображение записывается элемент с максимальным значением из каждого окна 2×2 элемента. В соответствии с результатами исследований из [22], данный алгоритм подвыборки работает лучше других, так как сокращает вычисления и обеспечивает независимость результата процедуры от изменения входных данных. Поэтому он и был выбран нами, что важно для увеличения производительности разрабатываемого устройства.
Для извлечения ключевых признаков весовые коэффициенты процедуры свёртки настраиваются с использованием обучающей выборки. Существует множество обучающих выборок, собранных для решения различного рода задач. С учётом поставленной задачи распознавания рукописных цифр, хорошо подходит база изображений рукописных цифр MNIST [4, 23]. Сегодня она содержит 60000 обучающих и 10000 тестовых пар (изображение – метка). Изображения нормализованы по размеру и отцентрированы. Размер каждой цифры не более 20×20 пикселей, но вписаны они в квадрат размером 28×28 пикселей.
Для решения задачи создания устройства необходимо не только обучить программно реализованную СНС, но и использовать полученные весовые коэффициенты свёрточных слоёв в дальнейшем при аппаратной реализации этой сети. В настоящее время существуют несколько библиотек программ для создания и обучения ИНС [24]. Ранее нами была выбрана библиотека Caffe, использующая для хранения весовых коэффициентов 32-разрядные числа с плавающей запятой [25], и предложена методика переноса весовых коэффициентов для их использования в аппаратной реализации СНС [26]. Эта библиотека позволила программно реализовать СНС предложенной архитектуры и провести её обучение на обучающей выборке из базы MNIST .
Обучение CНС проводилось с использованием процедур из библиотеки Caffe, реализующих метод обратного распространения ошибки и один из методов оптимизации – метод стохастического градиентного спуска (англ. Stochastic Gradient Decent – SGD ) [13, 14]. Параметры оптимизации взяты из обучающих примеров библиотеки. За одну итерацию выбиралось одно изображение из обучающей выборки. Всего осуществлялось 600000 итераций. Так как изображения из базы MNIST являются одноканальными, а на вход предлагаемой СНС необходимо подать трехканальное изображение, то на её вход одномоментно подавались три копии изображения. В качестве функции потерь (англ. loss function ) использовалась сумма квадратов разности между ожидаемым и полученным значением на выходе СНС. Веса сети инициализировались по методу Завьера [27].
-
3. Аппаратная реализация свёрточной нейронной сети
-
3.1. Блоки базовых операций над числами
В аппаратной СНС вычислительные блоки будут двух типов, реализующих соответственно процедуры свёртки и подвыборки. Поскольку в архитектуре СНС используются процедуры свёртки с разными значениями параметров, то при аппаратной реализации первого слоя необходимо 6 вычислительных блоков свёртки, для второго слоя – 6 вычислительных блоков подвыборки, для реализации третьего слоя – 32 блока свёртки, четвертого – 32 блока подвыборки. Для пя- того слоя необходимо 100 вычислительных блоков свёртки, а для шестого (полносвязного) – 10 блоков свёртки. Такие параллельно выполняемые вычислительные блоки используются в каждом слое с учётом того, что в СНС выходные карты признаков формируются независимо друг от друга.
Исходя из анализа архитектуры СНС, можно считать, что основными (базовыми) операциями при вычислениях являются сложение, умножение (используются в процедуре свертки) и операция выбора максимального числа (используется в процедуре подвыборки). При этом вычисления ведутся над числами с плавающей запятой. Однако во многих ПЛИС, в том числе в используемой нами, отсутствуют встроенные блоки для выполнения операций с плавающей запятой. В этой связи необходимо было реализовать базовые операции над числами с плавающей запятой.
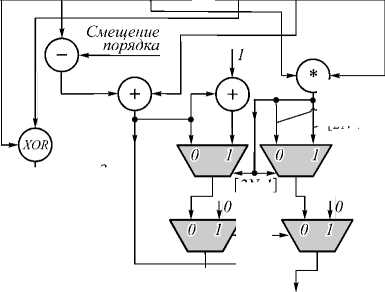
На рис. 2 показана функциональная схема разработанного базового блока (субблока – входит в состав вычислительного блока свёртки), реализующего операцию умножения над числами с плавающей запятой.
mult
________ Число 2 ________
Знак | Порядок | Мантисса
_________ Число 1 _________
Знак ^Порядок! Мантисса
[2N-1\
Знак сложения порядков
Знак | Порядок | Мантисса Произведение
Рис. 2. Функциональная схема блока, реализующего операцию умножения
A2N-LNA ^\2N-2:N-1}
Знак результата операции умножения получается путём выполнения логической операции исключающего ИЛИ над знаками множителей. Порядок произведения выбирается в зависимости от старшего бита результата умножения мантисс либо как сумма порядков множителей, либо как её инкремент. Мантисса произведения выбирается в зависимости от старшего бита результата умножения мантисс так: либо старшие N бит произведения мантисс, либо старшие N бит произведения мантисс, взятые на один разряд правее.
Аппаратная реализация операции сложения над числами с плавающей запятой является более сложной задачей, чем реализация операции умножения. Основная проблема в том, что согласно стандарту IEEE 754, необходимо сначала привести два числа к одному порядку, а затем произвести сложение [28]. Однако это требует больших вычислительных ресур- сов, поэтому операция сложения была реализована согласно работе [29], что позволило сократить использование ресурсов ПЛИС.
В соответствии с этим подходом была разработана функциональная схема блока, реализующего данную
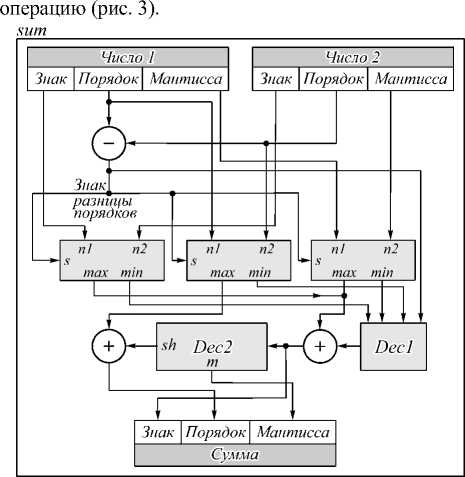
Рис. 3. Функциональная схема блока, реализующего операцию сложения
В субблоке упорядочивания исходных чисел на выход max подается n 1, а на выход min – n 2, если признак максимального числа s = 1; если же признак s =0, то max= n 2, min = n 1. Признак максимального числа s вычисляется на основе разницы порядков операндов. Субблок Dec 1 преобразует знак, порядок и мантиссу минимального слагаемого и формирует на выходе нормализованную мантиссу с учётом разницы между порядками слагаемых. Субблок Dec 2 формирует значение смещения для порядка максимального операнда, а на выходе m – мантисса суммы. На вход Dec 2 поступает результат сложения мантисс. Знак суммы вычисляется в результате сложения нормализованной мантиссы (выход Dec 1) и мантиссы максимального операнда со знаком. Мантисса суммы формируется на основе поиска первой старшей единицы в субблоке Dec 2. Порядок суммы вычисляется путём сложения порядка максимального операнда со значением смещения (выход sh субблока Dec 2).
Рассмотрим аппаратную реализацию операции выбора максимального числа . Она основана на вычислении разниц между порядками и мантиссами двух чисел с плавающей запятой. Функциональная схема базового блока comp для такой операции представлена на рис. 4.
Результат сравнения знаков входных чисел формируется логической операцией исключающего ИЛИ. Результаты сравнения порядков и мантисс чисел кодируются 0 или 1 в зависимости от знака разности. Dec декодирует поступающие на входы результаты сравнения знаков, порядков и мантисс входных чисел. Выбор максимального числа зависит от значения выхода элемента Dec: если оно равно 0, то максимальное число 1, если – 1, то число 2. На выход блока подается максимальное число.
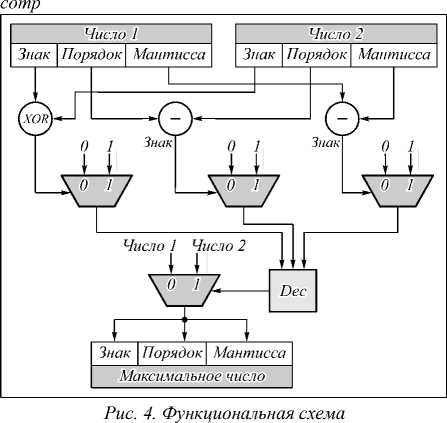
блока выбора максимального числа
3.2. Вычислительные блоки свёртки и подвыборки
Блоки (субблоки), реализующие базовые операции, использовались при создании вычислительных блоков свёртки и подвыборки. Так, для реализации блока свёртки используются блоки базовых операций умножения и сложения. Описание входных и выходных сигналов на функциональной схеме этого блока следующее (рис. 5): 1 – вход для значений весовых коэффициентов; 2 – входные значения нейронов; 3 – управляющий сигнал для вычисления свёртки; 4 – сигнал сброса автоматов; 5 – управляющий сигнал для окончания свёртки; 6 – вход для значения смещения нейрона; 7 – выходное значение нейрона.
Conv
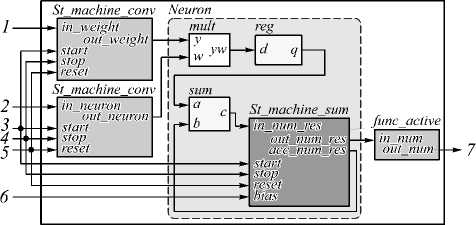
Рис. 5. Функциональная схема блока свёртки
Вычислительный блок свёртки содержит в себе субблок нейрона ( Neuron ) и управляющие автоматы St_machine_conv . Субблок Neuron состоит из автомата St_machine_sum и блоков операции умножения и сложения. Способ включения этих блоков операций позволяет организовать двухэтапный конвейер.
После поступления управляющего сигнала 3 начинают свою работу автоматы St_machine_conv и St_machine_sum. Два управляющих автомата St_machine_conv обеспечивают синхронизацию с внешними блоками, сброс и подачу входных значений и весов, считанных из блоков памяти SRAM, на нейрон. Автомат St_machine_sum обеспечивает функцию накопления после операции сложения. Автомат спроектирован с учётом возможности использования в нейросети значений смещения (bias на рис. 5). По умолчанию смещение на всех слоях равно 0.
Работа конвейера в субблоке Neuron происходит следующим образом. В момент времени t выполняет- ся умножение двух элементов и сложение результата умножения t–1 с предыдущими значениями суммы (накопления). Результат умножения хранится в промежуточном регистре reg. Данное решение позволяет одновременно выполнять две операции с плавающей запятой, что приводит к увеличению производительности устройства.
Разработанная функциональная схема вычислительного блока подвыборки представлена на рис. 6.
Pool
St machine poolign
comp
m_num_res start stop in_num
outjuim 1 out_num2
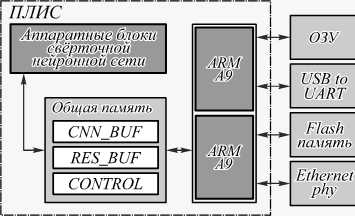
out_m • numl res - num2 Рис. 6. Функциональная схема блока подвыборки Описание входных и выходных сигналов на схеме следующее: 1 – управляющий сигнал для начала подвыборки; 2 – управляющий сигнал для окончания подвыборки; 3 – сигнал сброса автомата; 4 – входные значения для блока; 5 – выходное значение для блока. После поступления управляющего сигнала 1 начинает свою работу автомат St_machine_pooling, который обеспечивает синхронизацию с внешними блоками, сброс и подачу входных значений, считанных из блока памяти SRAM, на элемент comp. Затем происходит подача значений со входа 4 на выход автомата out_num1 и значений входа in_num_res на out_num2. Значения на входе in_num_res формируются блоком comp. По завершении процедуры подвыборки получаем максимальное число ядра 2×2, которое подаётся на выход 5. Такая реализация позволяет производить поиск максимального числа за количество тактов, равное числу элементов в ядре. 3.3. Контроллеры памяти 4. Особенности разработанного устройства При аппаратной реализации СНС необходимо хранить входные, промежуточные и выходные данные нейросети, а также в разных слоях следует обеспечить различные варианты доступа к памяти блокам свёртки и подвыборки. Для этого необходимы контроллеры памяти трёх видов. Первый из них – контроллер памяти для чтения входных и промежуточных значений карт признаков. Он используется в двух режимах: работа с общей памятью CM и разделенной памятью CI. Другой контроллер памяти CO предназначен для записи выходных значений слоев нейросети. Последний из них – контроллер памяти CW – обеспечивает чтение весовых коэффициентов связей между нейронами в слоях свёртки Рис. 7. Функциональная схема СНС Структурная схема созданного устройства на ПЛИС с учётом окружения на плате Terasic SoCkit показана на рис. 8, а фотография устройства – на рис. 9. Отладочная плата Terasic SoCkit Подклю чение по RS-232 Подключение по SSH Рис. 8. Структурная схема устройства для распознавания рукописных цифр Взаимодействие между аппаратной реализацией СНС и двухъядерным процессором ARM Cortex – A9 происходит через область общей памяти, к которой имеют доступ как аппаратная СНС, так и ядра процессора. Область общей памяти разделена на несколько полей, которые имеют различное функциональное назначение. Область CNN_BUF является входной памятью для работы СНС. Область RES_BUF является памятью для записи результатов с выходов нейронной сети. CONTROL – регистр управления нейронной сетью. Взаимодействие с устройством происходит через терминалы по протоколам RS-232 или SSH. Рис. 9.Устройство для распознавания рукописных цифр на основе платы Terasic SoCkit При реализации СНС на ПЛИС изначально планировалось использование 32-разрядного представления чисел с плавающей запятой, как наиболее распространённого формата чисел в случае СНС. Однако при синтезе устройства выяснилось, что для работы с числами в этом формате необходимо в 1,38 раза больше ресурсов (логических ячеек, регистров и т.п.), чем имеется у используемой ПЛИС. Поэтому было решено применять другие форматы представления чисел. В настоящее время при реализации СНС начинают использовать формат чисел с плавающей запятой половинной точности [30, 31]. Блоки базовых операций, описанные выше, позволяют проводить операции над числами с плавающей запятой других форматов, в том числе и этого формата. Первый вариант созданного устройства позволяет работать с числами с плавающей запятой формата половинной точности (16 разрядов). Второй вариант устройства использует формат 15-разрядного представления чисел с плавающей запятой. Данный формат не описан стандартом IEEE [28] и является собственным форматом. Он получен в результате сокращения на 1 бит мантиссы 16-разрядного представления числа с плавающей запятой. Остальные три варианта устройства с 14-, 13-, 12-разрядным представлением чисел получены таким же образом. Для оценки работоспособности всех вариантов устройства были проведены их логическая и физическая верификации. На этапе логической верификации проводилось сравнение значений выходов нейронов в устройстве, полученных моделированием работы устройства в программном пакете ModelSim [32], со значениями соответствующих выходов нейронов при программной реализации СНС. На этапе физической верификации значения выходов нейронов, полученные с помощью устройства и считанные при помощи программы SignalTapII [32], сравнивались с результатами логического моделирования. Верификация показала, что все пять вариантов устройства работоспособны. 5. Исследование эффективности программных и аппаратных реализаций СНС Эффективность всех вариантов устройства исследовалась в части их производительности, точности распознавания рукописных цифр и энергопотребления. С целью сравнения исследовались эти же три параметра ещё для двух установок, на которых исполнялась программная реализация СНС той же архитектуры. В качестве первой установки использовался персональный компьютер (ПК) с процессором AMD Phenom II 925 с тактовой частотой 2,8 ГГц и ОЗУ DDR3-1333 МГц. На ПК была реализована СНС, использующая 32-разрядные числа с плавающей запятой (вариант установки назван ПК_32), и реализована СНС, использующая 16-разрядные числа (вариант ПК_16). В состав другой установки входили двухъядерный процессор ARM – Cortex A9 с тактовой частотой 800 МГц и ОЗУ DDR3-800 МГц системы на кристал- ле Cyclone V SX. Программная реализация СНС на этой установке также выполнялась в двух вариантах: работа с 32-разрядными числами (вариант установки A_32) и с 16-разрядными числами (вариант A_16). Для реализации в первой и второй установках операций над 16-разрядними числами с плавающей запятой использовалась библиотека Half-precision floating point library из [33]. Программные реализации СНС компилировались с флагом оптимизации компилятора GCC – O2, а их выполнение проходило в одном потоке под управлением ядра ОС Linux в консольном режиме. Третья установка аналогична первой, но в её состав дополнительно входит видеокарта Nvidia GTX 1060, на которой производятся основные вычисления. При программной реализации СНС предложенной архитектуры на данной установке использовалась модифицированная компанией Nvidia библиотека Caffe – NVCaffe, в которую добавлены программы поддержки операций над числами формата половинной точности [34]. Благодаря этому можно провести реализацию СНС на видеокарте при выполнении операции с 32-разрядными числами (вариант установки ГП_32) и с 16-разрядными числами (вариант ГП_16). Варианты разработанного устройства в зависимости от формата представления чисел с плавающей запятой далее обозначены как АП_16, АП_15, АП_14, АП_13, АП_12. Тактовая частота аппаратных реализаций СНС – 50 МГц. Исследования эффективности разработанных вариантов устройства и вариантов СНС на трех установках проводились с использованием 10000 тестовых изображений рукописных цифр из базы MNIST. Результаты исследования точности распознавания рукописных цифр представлены в табл. 1, где Qпр – средняя точность распознавания цифр программным способом, а Qап – средняя точность, полученная аппаратным способом. Табл. 1. Результаты исследования точности распознавания рукописных цифр Точность, % Формат числа, бит Qпр Qап 32 98,71 - 16 98,64 98,34 15 – 98,33 14 – 98,27 13 – 97,85 12 – 93,48 Средние значения Qпр и Qап получены с учётом всех 10000 результатов распознавания цифр. Значения Qпр для ПК_32 и A_32 и ГП_32 (первая строка в табл. 1), а также для ПК_16 и А_16 (вторая строка) совпадают. Кроме того, совпадают значения точности для ГП_32 и ГП_16. Будем считать значение Qпр для вариантов установок ПК_32, А_32 и ГП_32 за эталонное. Падение точности распознавания при использовании вариантов установок ПК_16 и А_16 относительно эталона невелико (на 0,07 %), однако оно значительно больше при аппаратной реализации СНС для варианта устройства АП_16 (0,37 %). Падение точности для всех вариантов устройства объясняется использованием упрощённой процедуры аппаратного сложения двух чисел с плавающей запятой. Следует отметить, что усечение мантиссы на 1–2 бита у вариантов АП_15 и АП_14 по сравнению с вариантом устройства АП_16 не сильно ухудшает точность распознавания. Варианты устройства АП_13 и АП_12 из-за невысокой точности распознавания рукописных цифр, по-видимому, не будут востребованы в практических приложениях. Заметим, что результаты исследований точности распознавания согласуются с результатами из [35], где также сделан вывод о падении точности при уменьшении разрядности представления весовых коэффициентов СНС. Результаты исследования производительности вариантов устройства и трёх установок представлены в табл. 2, где Тоб – среднее время, за которое происходит распознавание одного тестового изображения из базы MNIST, начиная с его загрузки в память устройства и заканчивая получением результата распознавания, а Тпп – среднее время работы СНС по распознаванию одной тестовой цифры. Относительная ошибка измерений – не более 3 %. Видим, что производительность всех вариантов устройства ниже, чем у вариантов установки ГП_32 и ГП_16 и близка к производительности ПК_32, но значительно превосходит производительность вариантов установок A_32, ПК_16 и особенно А_16. Иными словами, невзирая на малую тактовую частоту 50 МГц при аппаратной реализации СНС, производительность вариантов устройства высока за счёт параллельной работы вычислительных блоков. Разница между Тоб и Тпп для всех вариантов устройства может быть уменьшена путём организации прямого доступа ПЛИС к общей памяти устройства. Табл. 2. Результаты исследования производительности устройства и установок Время, мс Варианты устройства и установок Тоб Тпп ПК_32 3,042 2,980 ПК_16 21,331 21,264 А_32 11,489 11,200 А_16 99,144 97,296 ГП_32 0,822 0,774 ГП_16 1,704 1,652 АП_16 3,262 2,417 АП_15 3,266 2,417 АП_14 3,270 2,418 АП_13 3,265 2,417 АП_12 3,271 2,418 В табл. 3 представлены результаты измерения энергопотребления P вариантов устройства и трёх установок. Относительная ошибка измерений не более 3 %. Самым низким энергопотреблением обладают варианты установок A_32 и A_16. Немногим больше энергии, чем А_32 и А_16, потребляет каждый из вариантов устройства, однако это потребление в десятки раз меньше, чем у ПК_32, ПК_16, ГП_32 и ГП_16. Табл. 3. Энергопотребление вариантов устройства и установок Энергопотребление, Вт Варианты устройства и установок P ПК_32 126,0 ПК_16 126,0 А_32 4,8 А_16 4,8 ГП_32 149,1 ГП_16 138,1 АП_16 5,1 АП_15 5,1 АП_14 5,1 АП_13 5,1 АП_12 5,1 В табл. 4 сведены результаты исследований эффективности разработанных вариантов устройства и требуемые для реализации этих вариантов вычислительные ресурсы ПЛИС: количество используемых логических ячеек LUT и регистров REG. Табл. 4. Результаты исследований вариантов устройства и требуемые ресурсы ПЛИС Варианты устройства Ресурсы ПЛИС Qап, % Тоб, мс P, Вт LUT, шт REG, шт АП_16 64 114 20 598 98,34 3,262 5,1 АП_15 56 928 19 733 98,33 3,266 5,1 АП_14 53 699 18 868 98,27 3,270 5,1 АП_13 49 720 18 003 97,85 3,265 5,1 АП_12 43 829 17 138 93,48 3,271 5,1 Из табл. 4 следует, что при уменьшении длины мантиссы чисел на 1 разряд наблюдается сокращение количества ресурсов (LUT и REG), используемых каждым из вариантов устройства, на 6– 11 %. При этом падение точности распознавания остается в пределах 1 %, кроме варианта устройства АП_12. Это указывает на возможность достижения компромисса между требованием к устройству по точности распознавания рукописных цифр и количеством необходимых для этого вычислительных ресурсов ПЛИС. Производительность и энергопотребление вариантов устройства практически не зависят от количества используемых вычислительных ресурсов ПЛИС, что важно при проектировании и эксплуатации таких мобильных устройств. Заключение Предложена архитектура СНС, подобная известной архитектуре LeNet5, для распознавания рукописных цифр. Учитывая значительную вычислительную сложность такой сети и весьма жёсткие требования к производительности и энергопотреблению мобильного устройства для распознавания рукописных цифр, решено было разработать его на основе ПЛИС-системы на кристалле Cyclone V SX. Была программно реализована предложенная СНС, которая обучалась на изображениях рукопис- ных цифр из известной базы MNIST. Полученные при обучении весовые коэффициенты сети затем использовались при её аппаратной реализации на ПЛИС. На базе платы Terasic SoCkit, включающей ПЛИС с аппаратно реализованной СНС, создано пять вариантов устройства, отличающихся форматами представления чисел с плавающей запятой. Проведены исследования точности распознавания рукописных цифр каждым из вариантов устройства и программно реализованной СНС на трёх различных вычислительных установках. Выяснилось, что программно реализованная СНС позволяет более точно распознавать цифры, чем любой из вариантов устройства. Однако варианты устройства с 16-, 15- и 14-разрядным представлением чисел с плавающей запятой дают практически приемлемые результаты распознавания рукописных цифр. Исследования производительности и энергопотребления вариантов устройства и трёх установок, на которых программно исполнялась СНС, показали, что за счёт параллельной работы вычислительных блоков производительность всех вариантов устройства близка к производительности используемого ПК с процессором AMD Phenom 925, но ниже, чем у установки с этим же ПК и видеокартой компании Nvidia. При этом энергопотребление каждого из вариантов устройства в десятки раз меньше, чем у этого же ПК и тем более чем у установки, в состав которой входят ПК и видеокарта. Полученные результаты разработки и исследований указывают на перспективность аппаратной реализации на ПЛИС с ограниченными вычислительными ресурсами СНС предложенной архитектуры и, соответственно, на возможность создания мобильных и энергоэффективных устройств для распознавания рукописных цифр с использованием этой сети. Исследования были поддержаны грантом Программы повышения конкурентоспособности Томского политехнического университета, проект № ВИУ-ИК-110/2017.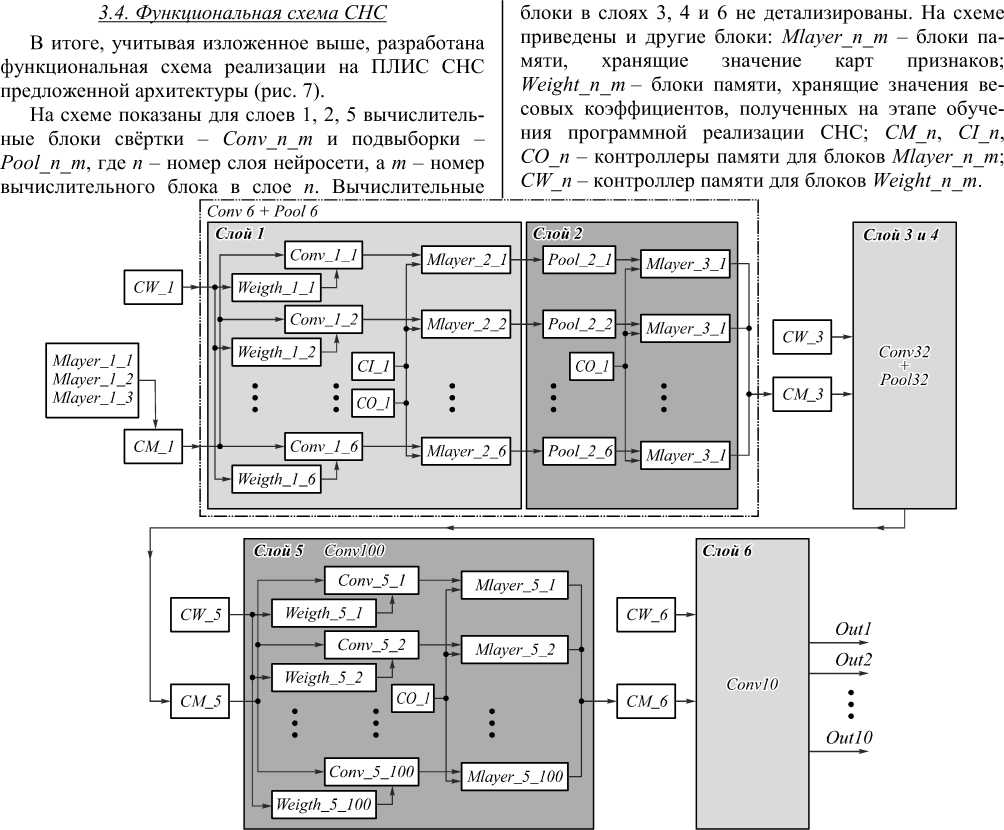

Список литературы Устройство на основе ПЛИС для распознавания рукописных цифр на изображениях
- Chatfield, K. Return of the devil in the details: Delving deep into convolutional nets/K. Chatfield, K. Simonyan, A. Vedaldi, A. Zisserman//Proceedings of the British Machine Vision Conference. -2014. - DOI: 10.5244/c.28.6
- Russakovsky, O. ImageNet large scale visual recognition challenge/O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A.C. Berg, L. Fei-Fei//International Journal of Computer Vision. -2015. -Vol. 115, Issue 3. -P. 211-252. - DOI: 10.1007/s11263-015-0816-y
- Goyal, S. Object recognition using deep neural networks: A survey /S. Goyal, P. Benjamin. -2014. -URL: https://arxiv.org/pdf/1412.3684.pdf (request date 26.07.2017).
- LeCun, Y. Gradient-based learning appelied to document recognition/Y. LeCun, L. Bottou, Y. Bengio, P. Haffner//Proceedings of the IEEE. -1998. -Vol. 86, Issue 11. -P. 2278-2324. - DOI: 10.1109/5.726791
- Reshma, A.J. An overview of character recognition focused on offline handwriting/A.J. Reshma, J.J. James, M. Kavya, M. Saravanan//ARPN Journal of Engeneering and Applied Sciences. -2016. -Vol. 11, No. 15. -P. 9372-9378.
- Tuba, E. Handwritten digit recognition by support vector machine optimized by bat algorithm/E. Tuba, M. Tuba, D. Simian//Proceedings of the 24th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision (WSCG 2016). -2016. -P. 369-376.
- Спицин, В.Г. Применение вейвлет-преобразования Хаара, метода главных компонент и нейронных сетей для оптического распознавания символов на изображениях в присутствии импульсного шума/В.Г. Спицин, Ю.А. Болотова, Н.Х. Фан, Т.Т.Ч. Буй//Компьютерная оптика. -2016. -Т. 40, № 2. -С. 249-257. - DOI: 10.18287/2412-6179-2016-40-2-249-257
- Elleuch, M. A new design based-SVM of the CNN classifier architecture with dropout for offline Arabic handwritten recognition/M. Elleuch, R. Maalej, M. Kherallah//Procedia Computer Science. -2016. -Vol. 80. -P. 1712-1723. - DOI: 10.1016/j.procs.2016.05.512
- Alom, M.Z. Handwritten bangla digit recognition using deep learning/M.Z. Alom, P. Sidike, T.M. Taha, V.K. Asari . -2017. -URL: https://arxiv.org/pdf/1705.02680.pdf (request date 10.10.2017).
- Maitra, D.S. CNN based common approach to handwritten character recognition of multiple scripts/D.S. Maitra, U. Bhattacharya, S.K. Parui//Proceedings of the 13th International Conference on Document Analysis and Recognition (ICDAR). -2015. -С. 1021-1025. - DOI: 10.1109/ICDAR.2015.7333916
- Glauner, P.O. Comparison of training methods for deep neural networks /P.O. Glauner. -2015. -URL: https://arxiv.org/pdf/1504.06825.pdf (request date 26.07.2017).
- Guerra, L. Comparison between supervised and unsupervised classifications of neuronal cell types: a case study/L. Guerra, L.M McGarry, V. Robles, C. Bielza, P. Larrañaga, R. Yuste//Developmental Neurobiology. -2011. -Vol. 71, Issue 1. -P. 71-82. - DOI: 10.1002/dneu.20809
- Bottou, L. Stochastic gradient descent tricks/L. Bottou. -In book: Neural networks: Tricks of the trade/ed. by G. Montavon, G.B. Orr, K.R. Müller. -Berlin, Heidelberg: Springer, 2012. -P. 421-436. - DOI: 10.1007/978-3-642-35289-8_25
- LeCun, Y.A. Efficient BackProb/Y.A. LeCun, L. Bottou, G.B. Orr, K.R. Müller. -In book: Neural networks: Tricks of the trade/ed. by G. Montavon, G.B. Orr, K.R. Müller. -Berlin, Heidelberg: Springer, 2012. -P. 9-48. - DOI: 10.1007/3-540-49430-8_2
- Солдатова, О.П. Применение свёрточной нейронной сети для распознавания рукописных цифр/О.П. Солдатова, А.А. Гаршин//Компьютерная оптика. -2010. -Т. 34, № 2. -С. 252-259.
- El-Sawy, A. CNN for handwritten arabic digits recognition based on LeNet-5/A. El-Sawy, E.L.B. Hazem, M. Loey//Proceedings of the International Conference on Advanced Intelligent Systems and Informatics 2016. -2016. -P. 566-575. - DOI: 10.1007/978-3-319-48308-5_54
- SoCKit -The development kit for new SoC device . -URL: http://www.terasic.com.tw/cgi-bin/page/archive.pl?CategoryNo=167&No=816 (request date 26.07.2017).
- Farabet, C. An FPGA-based stream processor for embedded real-time vision with convolutional networks/C. Farabet, C. Poulet, Y. LeCun//IEEE 12th International Conference on Computer Vision Workshops (ICCV Workshops). -2009. -P. 878-885. - DOI: 10.1109/ICCVW.2009.5457611
- Zhang, C. Optimizing FPGA-based accelerator design for deep convolutional neural networks/C. Zhang, P. Li, G. Sun, Y. Guan, B. Xiao, J. Cong//Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. -2015. -P. 161-170. - DOI: 10.1145/2684746.2689060
- Motamedi, M. Design space exploration of FPGA-based deep convolutional neural networks/M. Motamedi, P. Gysel, V. Akella, S. Ghiasi//21st Asia and South Pacific Design Automation Conference (ASP-DAC). -2016. -P. 575-580. - DOI: 10.1109/ASPDAC.2016.7428073
- Krizhevsky, A. ImageNet classification with deep convolutional neural networks/A. Krizhevsky, I. Sutskever, G.E. Hinton//Proceedings of the 25th International Conference on Neural Information Processing Systems. -2012. -Vol. 1. -P. 1097-1105.
- Scherer, D. Evaluation of pooling operations in convolutional architectures for object recognition/D. Scherer, A. Müller, S. Behnke. -In book: Artificial Neural Networks -ICANN 2010/ed. by K. Diamantaras, W. Duch, L.S. Iliadis. -Berlin, Heidelberg: Springer, 2010. -Part III. -P. 92-101. - DOI: 10.1007/978-3-642-15825-4_10
- The MNIST database of handwritten digits . -URL: http://yann.lecun.com/exdb/mnist (request date 26.07.2017).
- Bahrampour, S. Comparative study of deep learning software frameworks/S. Bahrampour, N. Ramakrishnan, L. Schott, M. Shah . -2016. -URL: https://arxiv.org/pdf/1511.06435.pdf (request date 26.07.2017).
- Jia, Y. Caffe: Convolutional architecture for fast feature embedding/Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, S. Guadarrama, T. Darrell//Proceedings of the 22nd ACM international conference on Multimedia (MM '14). -2014. -P. 675-678. - DOI: 10.1145/2647868.2654889
- Береснев, А.П. Методика переноса весов нейронной сети из программной в аппаратную реализацию/А.П. Береснев, И.В. Зоев, А.Н. Мальчуков. -В кн.: Сборник трудов XIV Международной научно-практической конференции студентов, аспирантов и молодых ученых. -Томск: Изд-во ТПУ, 2016. -Т. 1. -С. 22-23
- Glorot, X. Understanding the difficulty of training deep feedforward neural networks/X. Glorot, Y. Bengio//Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS). -2010. -P. 249-256.
- 754-2008: IEEE standard for floating-point arithmetic. -Revision of ANSI/IEEE Std 754-1985. -New York: IEEE Publisher, 2008. - DOI: 10.1109/IEEESTD.2008.4610935
- Zoev, I.V. Implementation of 14 bits floating point numbers of calculating units for neural network hardware development/I.V. Zoev, A.P. Beresnev, E.A. Mytsko, A.N. Malchukov//IOP Conference Series: Materials Science and Engineering. -2017. -Vol. 177, Issue 1. -012044. - DOI: 10.1088/1757-899X/177/1/012044
- Tavallaei, S. Microsoft project Olympus hyperscale GPU accelerator (HGX-1) /S. Tavallaei. -2017. -URL: https://azure.microsoft.com/mediahandler/files/resourcefiles/00c18868-eba9-43d5-b8c6-e59f9fa219ee/HGX-1%20Blog_5_26_2017.pdf (request date 10.10.2017).
- Sánchez, O.M. Adapting deep neural networks to a low-power environment /O.M. Sánchez. -2017. -URL: https://upcommons.upc.edu/bitstream/handle/2117/106673/126470.pdf (request date 10.10.2017)
- Quartus II handbook volume 3: Verification . -2015. -URL: https://www.altera.com/content/dam/altera-www/global/en_US/pdfs/literature/hb/qts/qts_qii5v3.pdf (request date 26.07.2017).
- Half 1.12. IEEE 754-based half-precision floating point library . -URL: http://half.sourceforge.net/index.html (request date 10.10.2017).
- NVIDIA: Caffe . -URL: https://github.com/NVIDIA/caffe (request date 10.10.2017).
- Rastegari, M. XNOR-Net: ImageNet classification using binary convolutional neural networks/M. Rastegari, V. Ordonez, J. Redmon, A. Farhadi//Proceedings of the European Conference on Computer Vision. -2016. -P. 525-542. - DOI: 10.1007/978-3-319-46493-0_32


