Уточнение закона Био-Савара-Лапласа

Закон Био-Савара-Лапласа (БСЛ) получен экспериментально и его формула имеет известный вид:

|r-r I                                 (1)

Принято считать, что «этот закон является следствием двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля» [1]. Вывод заключается в следующем. Вводится векторный потенциал, удовлетворяющий уравнению

H=rot(A), (2) и условие калибровочной инвариантности div(A)=0. (3) Путем преобразования этих уравнений выводится закон БСЛ в виде уравнения (1). Этот закон устанавливает зависимость магнитной напряженности от постоянного тока проводимости. Известно также уравнение Максвелла, связывающее магнитную напряженность с постоянным током проводимости, а именно

ГО^Я) = J. (4)

Принято считать, что уравнение (4) является дифференциальной формой записи уравнения (1). Доказательство этого утверждения отсутствует. А ниже будет приведено доказательство того, что эти уравнения противоречивы. Отсюда следуют два утверждения

• 1.    Если согласиться с тем, что все явления в области электродинамики описываются уравнениями Максвелла, то необходимо признать, что уравнение (1) не является строгим и требует уточнения. Но это ни в коей мере не умаляет заслуги авторов этого закона, которые сумели его обнаружить и сформулировать на пустом месте, когда неоткуда было ждать подсказок. Уточнению этого закона посвящена предлагаемая статья.

• 2.    Векторный потенциал не имеет формальной связи с уравнениями Максвелла. Заметим еще, что условие калибровочной инвариантности может быть выполнено множеством способов, что привносит в физику произвол, который противоречит самому духу классической физики. В то же время применение этого условия в указанном доказательстве служит обоснованием дальнейшего использования векторного потенциала и в других областях физики [2]. Но поскольку векторный потенциал не имеет формальной связи с уравнениями Максвелла, его применение лишено этого обоснования.

2.    Математическая модель

Далее будет показано, что, по крайней мере, для длинного провода без векторного потенциала можно обойтись и решение получается полным, подтвержденным экспериментально, но более сложным, чем в существующем законе Био-Савáра-Лапласа.

В [3] показано, что уравнения Максвелла для провода с постоянным током имеют вид rot(/) = 0,(а)

rot(H)—J—Jo = 0,(b)

div(J) = 0,(с)

div(H) = 0.(d)

где H , J — магнитные напряженности и плотности токов. Мы будем использовать цилиндрические координаты г, ф, z и рассматривать

• •    плотность основного тока оси oz J _o ,

• •    плотности дополнительных токов J _r , J ф , J _z ,

• •    магнитные    напряженности     Н _г , H ф , H _z — радиальная,

окружная и продольная соответственно.

Важно отметить, что используется полная система уравнений Максвелла, а не сокращенная система двух уравнений ( b, d ), которая считается приемлемой для магнитостатики. Такая сокращенная система не позволяет найти решение даже для провода с постоянным током. Напротив, полная система уравнений позволяет найти это решение и найти уравнения для потока энергии внутри (а не снаружи) провода.

В [3] подробно рассматривается решение уравнений Максвелла для провода постоянного тока и доказывается, что решение существует только при ненулевых дополнительных токах J r , J ^ , J . Решение имеет следующий вид:

7г = 7г (г)cos( аф + /z), ф<р = j< (г)sin( аф + /z),

Jz = jz (r)sin( a< + /z),

Hг = hr (г) cos( a< + /z),

H< = h< (r)sin( a< + /z),

Hz = hz (г) sin( a< + /z), где

;(г), к(г) - некоторые функции координаты г, а, / — некоторые константы.

В [3] доказано, что в проводе постоянного тока траектория точки с постоянной плотностью тока и постоянной магнитной напряженностью на цилиндре постоянного радиуса является винтовой линией. Кроме того, через каждую окружность проходит множество траекторий, на которых напряженности и плотности токов изменяются синусоидально в зависимости от ϕ. Следовательно, линия на цилиндре постоянного радиуса r , по которой точка движется так, что все напряженности и плотности токов остаются постоянными, является винтовой линией.

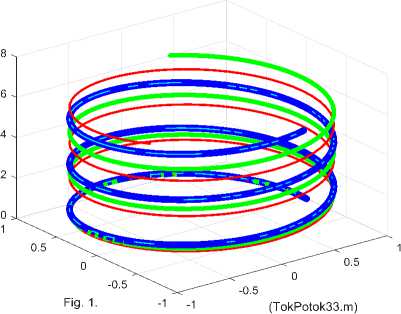
Например, на рис. 1 показаны три винтовые линии, описываемые функциями тока: толстая линия при а = 2, X = 0.8, средняя линия при а = 0.5, X = 2 и тонкая линия при а = 2, X = 1.6.

Далее будет показано, что и вне провода (где отсутствует ток) линия с постоянной магнитной напряженностью на цилиндре постоянного радиуса является винтовой линией.

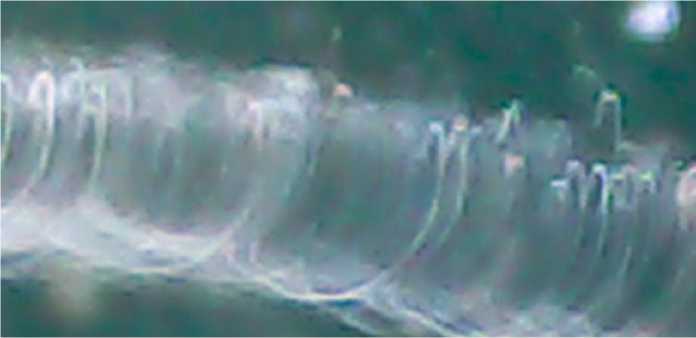
Рис. 2.

Сам факт существования вокруг проводника с постоянным током магнитного поля, имеющего спиралеобразную конфигурацию, установлен еще Эрстедом в 1820 г. [127, стр. 184].

На рис. 2 показана фотография провода, смоченного магнитной жидкостью (увеличено в 20 раз). Видны спиральные линии, образуемые магнитной жидкостью. Эта фотография свидетельствует о существовании спиральных линий магнитной напряженности.

3.    Напряженности в окрестности провода

Полученное в [3] решение позволяет найти магнитное поле, создаваемое током вне провода . Для этого достаточно взять решение при г > R, где R - радиус провода. При этом находим, что магнитные напряженности вне провода определяются следующими формулами:

^z (г) + hz (г) - hz (г) (— + 1) = 0(1)

к„(г) = -^,(2)

Мг) = у М'г).(3)

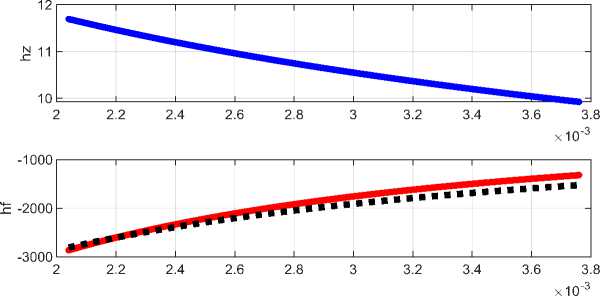
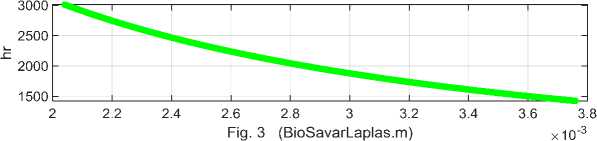
При известной функции ^г) могут быть найдены функции (2, 3). Решением уравнения (1) является модифицированная функция Бесселя. На рис. 3 представлены функции (1, 2, 3) при к= 0.25, / = 0.5,R = 0.002,г > R.(4)

В соответствии с законом БСЛ функция окружной магнитной напряженности бесконечно длинного провода имеет вид:

(г) = —.

4 пт

^b BSL

Эта формула, как частный случай закона БСЛ, многократно проверена экспериментально и в ней можно не сомневаться. Но наша задача состоит в том, чтобы уточнить закон БСЛ так, чтобы он стал действительным следствием уравнений Максвелла.

Во втором окне на рис. 3 пунктиром показана функция вида

Ь ф 2 (г) = ~^- .                             (6)

На этом примере видно, что функция (6) является хорошей аппроксимацией функции (2), т.е.

Ь ф 2 ⁽r)«h BSL ⁽r) .                                   (7)

Таким образом, получена аналитическая зависимость между напряженностью   h-BSL(r),   перпендикулярной проводу и определенной законом БСЛ для бесконечно длинного провода, и результатом Ьф 2 (г) решения уравнений Максвелла для провода с постоянным током.

Закон БСЛ устанавливает, что отсутствуют другие проекции напряженности, создаваемой током в проводе, кроме ^BSL(r). Для того, чтобы закон БСЛ полностью являлся следствием уравнений Максвелла, надо предположить, что существуют еще напряженности, направленные вдоль радиуса провода Ьг (г) и вдоль оси hz (г) провода. Итак, уточненный закон БСЛ состоит в том, что провод с постоянным током создает в окрестности провода вектор магнитной напряженности, цилиндрические проекции которого определяются по (1, 2, 3)

Все эти напряженности создаются током на участке, перпендикулярном радиусу г . Таким образом, напряженности бесконечно длинного провода имеют вид (2.15, 2.16, 2.17), где входящие в эти формулы величины Ь(г) определяются по (1-3).

На рис. 4 показан годограф вектора напряженности ^т—* __ > __ >

Hzf = Hz + Hf, (8) где слагаемые векторы определены по (2.12, 2.13) при фиксированных значениях координат г, ф. Годограф построен при условиях (4) и г = 0.0026, ф = 0, Ьф (г) = -2000, bz (г) = 11. (9)

На проводе выделена точка с определенными значениями векторов й; IE. Их сумма йТ указана точкой на годографе. Следует обратить внимание на то, модуль вектора й_; значительно меньше модуля вектора й ; - см. также рис. 3. Это явилось причиной того, что авторы закона БСЛ не заметили эту проекцию напряженности. Значение проекций й ; и й_г совпадают по порядку величин. Видимо в те давние времена трудно было определить направление вектора магнитной индукции. В наше время й_г можно обнаружить экспериментально.

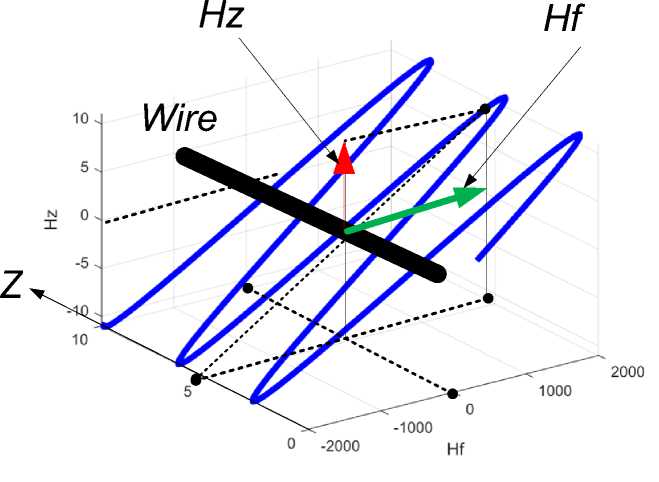
Рис. 4.

3.    Поток энергии

Рассмотрим энергетику взаимодействия тока в проводе с магниточувствительными элементами. Это взаимодействие требует затрат энергии от источника тока. Появление в окрестности провода ферритовой детали (например) вызывает увеличение тока и соответствующая дополнительная энергия расходуется на перемещение этой детали. Эта энергия может передаться детали только потоком энергии. Следовательно, кроме магнитного поля на деталь должен действовать поток электромагнитной энергии.

В [3] показано, что в окрестности провода, кроме магнитной напряженности, создается электрическая напряженность. Эти напряженности, по-прежнему, имеют вид (2.12-2.17), где для т >  R:

e'zQr) + eZ(r) ^ - ez(r) ^ + z2) = 0,(1)

_z х a e_z (г)

еф(Г = ;~,(2)

еЛГ = -^-eZOr),(3)

ez(R) = р- jz(R),(4)

где р - удельное соротивление. Плотность потока энергии, достигающей детали, определяется по формуле (как следует из [3])

Sv = Aez(T^‘ hт(т),(5)

где А — константа.

4.    Обсуждение

В [3] найдено решение уравнений Максвелла для провода с постоянным током. Приведенные выводы из этого решения обоснованы, по крайней мере, тем фактом, что они следуют из уравнений Максвелла.

Решение для провода с постоянным током легко переносится на область вне провода. Кроме того, это решение согласуется с экспериментом Эрстеда.

Существует уточненный закон БСЛ, являющийся следствием уравнений Максвелла. Уточнения сводятся к тому, что вектор магнитной напряженности, создаваемой постоянным током, направлен не строго перпендикулярно направлению тока, а имеет три проекции, причем величина окружной проекции превалирует.

Отсюда следует, что определение магнитной индукции в окрестности провода через дивергенцию векторного потенциала, является приближенным, а представление о том, что условие div(A)=0 естественным образом дополняет уравнения Максвелла, является неверным .

Уточненный закон БСЛ позволяет определить поток энергии, направленный от провода на магниточувствительный элемент.

6.    Эпилог

Векторный потенциал А вводится в уравнения Максвелла дополнением последних двумя строками:

ан rotCE) = -Ц -^,

(а)

div(E) = -Р (b) rot(H) = ] + Е^Е, (c) div(H) = 0, (d) rot(А) = рН, (e) div(А) = 0, (f) где р - плотность электрического заряда.

Сбросим с этих уравнений блистающую красоту векторной алгебры и получим 12 уравнений, которые в декартовых координатах имеют вид:

	дЕ2 _	дЕ у        дНх			(1)
	ду	" "27 = -РТ7	,
	дЕх "227"	дЕ2 _  „ дН у " "27 = -рТ7	,		(2)
	дЕ у	дЕх       дН2			(3)
	дх	" "27 = -рТ7	,
	дЕх  । дЕу  । дх    ду	дЕ. — _ р д2 =    Е ,			(4)
	дН2 ду	дН у     г " 17 = ! х + Е	дЕх дt ,		(5)
	дНх "27"	" дт = b + е дх      у	дЕ у дt ,		(6)
	дН у дх	дНх     ,   , - 77 = ] 2 + Е	дЕ2 дt ,		(7)
	дН х    дН у дх     ду	дН2 =о, д2			(8)
	дА2 ду	дАу _ „и - д2     рНх ,			(9)
	дАх 77-	д-А- = рНу , дх        у			(10)
	дА у "27-	дАх   „и ду     p 2 ,			(11)
	дАх | дАу  , 6 дх     ду     ।	'А7			(12)
		= о. 92
Из (1-3)	и (9-10) находим:
	д А дА2 _ дАу '	\     дНх	( дЕ 2	дЕу\	(13)
	дt V ду     д2 .	= Р-Г" = - )        дt	\ <)у	9z У,
	д 6ЭАх    дА2'	\     дН у	( дЕ х	_ дЕД	(14)
	дt \ д2     дх .	= Р.  = - /        дt	( д2	дх ',
	д ( дА у _ дАх	\     дН2	( дЕ у	_ дЕх Х	(15)
	дt \ дх     ду	) = Р-Е = - )       дt	( дх	ду /
В частности, из (13) получаем:

д дАу   д дАх _ дЕу дЕх

дt дх   дt ду     дх + ду или а дАу    дЕу at дх а аАх

дх , аЕх ду

at ду и т.д. В общем виде запишем:

д дАа дt дЬ

дЕ_а дЬ

Условия (16) выполняются только в том случае, если решение уравнений Максвелла является волновой функцией. Но волновая функция не может быть приемлемым для физики решением, поскольку не удовлетворяет закону сохранения энергии [3]. Таким образом, существование векторного потенциала противоречит закону сохранения энергии.