Уточненная модель термоупругопластического динамического деформирования гибких армированных цилиндрических оболочек

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2023PNRPU MECHANICS BULLETIN

Пластины и оболочки из композиционных материалов (КМ) широко используются в современной инженерии [1–6], причем они часто подвергаются интенсивному термосиловому нагружению [5–10], при котором материалы композиции могут деформироваться пластически [5; 8; 9; 11–14]. Поэтому актуальна проблема моделирования неизотермического упругопластического динамического деформирования тонкостенных элементов КМ-конструкций, которая на данный момент времени находится на стадии становления [5; 8; 9; 15–21]. В работе [21] была предложена математическая модель термоупругопластического деформирования многонаправленно армированного волокнами материала и проведены расчеты динамики гибких КМ-пластин из таких материалов. Однако аналогичное поведение оболочек до настоящего времени теоретически еще не рассматривалось.

Для моделирования волновых процессов в динамически изгибаемых тонкостенных КМ-конструкциях и учета их плохого сопротивления поперечным сдвигам традиционно используют простейшие неклассические теории Тимошенко – Рейсснера [4; 5; 8; 22–24], Амбарцумяна [21; 23; 25] и Редди [10; 26] или теории более высокого порядка точности [4; 7; 8; 20], использующие, как правило, гипотезу ломаной линии.

В [21] было показано, что при динамическом нагружении изгибаемых КМ-пластин разной относительной толщины температуру в поперечном направлении нужно аппроксимировать полиномом 7-го порядка. Изгибное же поведение армированных конструкций при этом описывалось теорией Амбарцумяна [25]. При кратковременном интенсивном силовом нагружении КМ-конструкций доминирующим источником тепловыделения служит диссипация механической энергии, представляющая собой полную свертку тензоров напряжений и скоростей деформаций [21; 27]. Поэтому, применяя различные теории изгибного поведения КМ-пластин и оболочек (Рейсснера, Редди, Амбарцумяна и более высоких порядков), можно с точностью разных порядков рассчитывать напряжения и скорости деформаций в армированных тонкостенных элементах конструкций, а значит и интенсивность тепловыделения в них. В работе [20] было показано, что упругопластическую (изотермическую) динамику армированных цилиндрических оболочек следует рассчитывать на базе уточненной теории их изгиба, а не на основе простейшего традиционно используемого ее варианта – теории Амбарцумяна. Следовательно, применение уточненной теории может привести к существенным поправкам в распределении температурного поля в таких КМ-конструкциях и их термомеханического отклика на внешние динамические нагрузки.

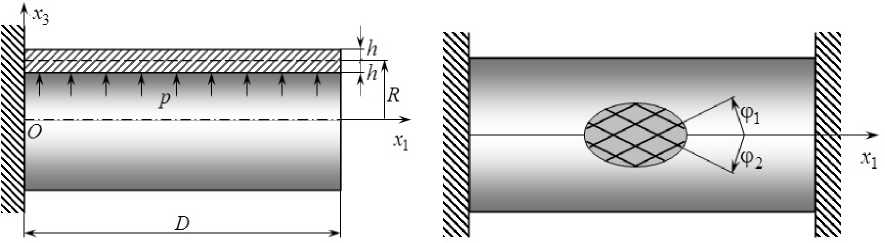
Рис. 1. Цилиндрические оболочки с жестким закреплением левой кромки ( а ) и с жестким закреплением обеих кромок ( b )

Fig. 1. Cylindrical shells with a rigid fixation of the left edge ( a ) and with a rigid fixation of both edges ( b )

Для численного интегрирования нелинейных динамических задач изгибаемых пластин и оболочек используют явные [8; 20; 21] и неявные [9; 28] (из семейства методов Ньюмарка) пошаговые схемы.

В силу всего вышеизложенного настоящая работа посвящена математическому моделированию неизотермической упругопластической динамики армированных гибких круговых цилиндрических оболочек при использовании уточненной теории их деформирования [20]. Связанная нелинейная термомеханическая начальнокраевая задача при этом численно интегрируется с применением явной пошаговой схемы [8; 20; 21].

1. Формулировка задачи и метод решения

Рассмотрим замкнутую круговую цилиндрическую оболочку радиуса R , длиной D и толщиной 2 h « min ( D , R ) (рис. 1), с которой свяжем цилиндрические координаты: x 1 - осевая (0 <  x 1 <  D ), x ₂ - окружная (0 <  x ₂ <  2 п ) и x 3 - радиальная ( R - h <  x 3 <  R + h ) координаты. Конструкция усилена N семействами волокон (возможно, пространственно) с плотностями армирования to _k (1 <  k <  N ). По толщине оболочки структура армирования однородна.

С каждым k -м семейством волокон свяжем ортогональную локальную систему координат x_i ^{( k )} так, что ось x ₁ ^{( k )} направлена вдоль траектории армирования. Ее ориентацию в пространстве x_j зададим углами сферической системы координат 9 _k и ф _k (рис. 2). Направляющие косинусы 1 — ⁾ локальных осей x ^{( k} ) в глобальной системе x - ( i , j = 1,3, ij

1 <  k <  N ) вычисляются по формулам (2.21) из [21].

Внешние распределенные касательные силы на лицевых поверхностях конструкции не учитываем. В случае пространственного армирования предполагается выполнение требования, предъявляемого к волокнистой структуре и изложенного в замечании в [21].

При традиционной перекрестной укладке волокон по эквидистантным цилиндрическим поверхностям (см. рис. 1, b , и рис. 2 при 9 _k = п /2) это требование выполняется заведомо. Согласно [20], при этом перемещения точек гибкой цилиндрической оболочки U_i и осреднён-ные деформации композиции е - в рамках уточненной теории изгиба запишутся так (геометрическая нелинейность моделируется в приближении Кармана):

M

U1 (t, r) = uv (t, x)- z51 w + £ f(”) (z ^m) (t, x), m=0

. . R + z

U2 ( t, r )= .. u 2 ( t, x ) + d 2 w + E f( ) ( z )е2з) ( t, x ),

R

U 3 ( t , r ) = w ( t , x ) ,     x = ( x 1 , x ₂ ) , r = ( x 1 , x ₂, x ₃ ) ;

M 1 ^е _п ( t , r ) = 5 1 u ^- z 5 j w + £ f ⁽ ) ( z Ц £2 1(3 ) +- ( 5 1 w ) , = 0                     ²

X

R + z

R

е22 (t, r)=^— X R + Z

M d2u2 +d2w + w + У f (m) (z)d2s(m) 22 2           2      223

m = 0

2 ^е 1 ₂ ⁽ t , r ) r + z

+

+ -

d 2 w ] R + z J

,

M d 2 U1 - z 5152 w +y f1(m) (z )d2 е1(зт)

m = 0

R + z

⁺ R 51 u 2 ⁺

+5 1 5 2 w +^5 / 2 m ) ( z ) d 1 s 2 m ) + -^ 5 1 w 6 2 w , m = 0                 ^{R +} z

_h ² - _z ² M ( _z A ^m , .

ei3 (t,r ) = —ГТ” Eki £3”) (t,x ),

h    m=0 V h J x3 ^ R + z, i = 1,2, x eQ, |z| < h, t > 10,

Q = { x :0 <  x 1 <  D , 0 <  x ₂ <  2 n } ,

+ (2)

где

f" (z) — 2[Ф" (z) — Ф"+2) (z■)]   (i = 1,2),

Ф*”) (z) —

m + 1 z

Ф^ ) — Rh + z ^V m ( z ) ^,

, _x   m — 1 (-1) l R l z m - ^l

^V m ( ² '   1        -- ^R m ln ( ^R + z ) ;

l = 0      m I

К равенствам (2) нужно присоединить двумерные уравнения движения гибкой цилиндрической оболочки (которые при учете выражений (1), (3) и (4) описываются формулами (13)–(15) и (17) из работы [20]) и определяющие уравнения для КМ, связывающие между собой скорости усредненных напряжений ст^, деформаций ёу и температуры 0. В данный момент времени t последние уравнения имеют следующий матричный вид [21]:

CT = Be + p,                       (5)

u ₁ , u ₂ – перемещения точек срединной поверхности ( z = 0) в осевом и окружном направлениях; w - прогиб точек этой же поверхности; z – введенная для удобства новая радиальная координата; t ₀ – начальный момент времени t ; M – целое число, задающее количество слагаемых в степенной аппроксимации деформаций поперечных сдвигов е i3 ; Q - область, занимаемая отсчетной поверхностью в координатах х 1 и x ₂; d i - оператор частного дифференцирования по координате x i ( i = 1,2). При значении M = 0 из равенств (1)-(3) получаются кинематические соотношения теорий Амбарцумяна [25] и Редди [10; 26]. В выражениях (1) и (2) неизвестны двумерные функции w , u i и e i ( m ⁾ ( i = 1,2, 0 <  m <  M ), зависящие и от времени t .

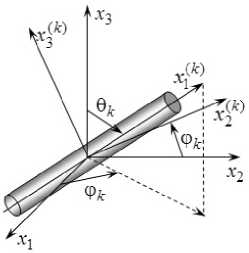
Рис. 2. Взаимная ориентация локальной (связанной с арматурой k -го семейства) и глобальной систем координат

Fig. 2. Mutual orientation of the local (associated with the reinforcement trajectory of the k -th family) and global coordinate systems

В данной работе КМ-оболочки рассматриваются как гибкие тонкостенные термомеханические системы, поэтому напряжение ст ₃₃ ( t , r ) в них с приемлемой для приложений точностью можно линейно аппроксимировать по z [24];

о(+)          r>               ст(+) (t xUст(—) (t

^U 33 ⁽ t , ^{x ) U} 33 ⁽ t , x ) ^U 33 ⁽ t , x ^{) + U} 33 ⁽ t , ^x )

^{;33 (} t ^{, r} ) =           2 h           ^{z +}             2            ^, (4)

x 6 Q, |z| < h,  t > t0, где G3±) (t, x) — ct33 (t, x, ± h) - нормальные напряжения на внутренней (–) и внешней (+) лицевых поверхностях конструкции, известные из силовых граничных условий.

где

T ст (ст , CT22, Cт33, CT23, CT31, СТ12 ) , е — (е11, е22, е33,2е23,2е31,2е12 ) ;

6 х 6-матрица B = ( b ij ) и шестикомпонентный

вектор-

столбец p = ( p₄ ) вычисляются по формулам (2.18) из [21] (которые здесь не приводятся в силу их громоздкости); точка – производная по времени t ; индекс T – операция транспонирования. Элементы Ъ_у и p i ( i , j = 1,6) матрицы B и вектора p определяются структурой армирования (углами 9 k , ф k и плотностями ю k ), физико-механическими характеристиками материалов фаз композиции и их текущим термомеханическим состоянием.

Согласно структуре вектор-столбцов <ст и е (см. (6)), из третьего уравнения системы (5) выразим скорость осредненной линейной поперечной деформации:

^е 33 = ^b 33 ^{( ст} 33    Р 3    ^b 31 ^e 11    ^b 32 ^e 22    ^{2 Ь} 34 ^е 23

^{— 2} b 35 ^e 31 ^— 2 b 36 ^e 12 ),

где скорость ст ₃₃ определяется дифференцированием по времени выражения (4), а скорости деформаций е._у в правой части получаются путем дифференцирования по t аппроксимаций (2), т.е. выражаются через двумерные функции w , vw , it_t и e i 3 m ) ( i = 1,2 , 0 <  m <  M ).

По толщине КМ-оболочки температуру 0 представим полиномом L -го порядка [21]:

L

0( t, r)—00=£© i(t, x) zl, l=0                               (8)

x 6Q,    |z| < h,    t > 10, где 00 = const - температура естественного состояния конструкции; 0l (0 < l < L) - двумерные функции, подлежащие определению.

Чтобы замкнуть постановку рассматриваемой связанной термоупругопластической задачи для КМ-оболо-чек, к соотношениям (1)–(8) нужно добавить уравнение теплового баланса (см. (4.5), (4.6) в [21]), механические (см. (24)–(26) в [20]) и тепловые (см. (4.7), (4.8) в [21]) граничные условия, заданные на кромках конструкций, а также начальные условия, заданные при t = 1 ₀ (см. (27), (28) в [20] и (4.22) в [21]).

Численное решение сформулированной нелинейной связанной начально-краевой задачи будем строить с использованием явной пошаговой схемы, т.е. неизвестные функции будем вычислять в дискретные моменты времени t = t n ( n = 0,1,2,...), причем предполагаем, что при t = t n _ 1 и t = t n заданы или определены значения следующих функций [20, 21]:

w ( x ) - w (tm , x) , ul”’ ( x ) - ul p) (tm , x) , mmn ry (p) == ry (t        СУ(±) fx^ — O"'1) (t X^ t/(r) fx^ —

° ij ( r ) ^- ° ij ( t m , r ) , ° 33 ( ^x )^- ° 33 ( t m , ^x ) , ^U ( ^x )^-

^- U ⁽ r ) ( t n , x ) , q i ( r )^- q i ( t n , r ) , @ s ( x )^- @ s ( t m , x ) ,

^ s ( x ) -® s ( t n __P x ) , q * ( x ) - q * ( t n , x ) ,       (9)

mm

° j ) ( r ) -° j ) ( t m , r ) , s j ) ( r ) -s j ) ( t m , r ) ,

X k ( r )^- X k ( t m , r ) , ^l = ^{1,2 0} <  P <  ^{M + 1} i , j = ^1,3

m = n - 1, n, 0 < r < L - 2, 0 < s < L, 0 < k < N, x e Q, |z| < h, конечно-разностными аналогами на трехточечном шаблоне {tn_1, tn, tn+1} . Это позволяет построить явную численную схему [20]. Заменив в двумерных приведенных уравнениях движения цилиндрической оболочки вторые производные по t от кинематических переменных w и ui(p) их конечными разностями, при учете выражений (1), (4) и (10), а также обозначений, аналогичных (9), получим [20]:

2 h П Г n + 1     n n _^       I ^{n n} n   _ⁿ      n \

—— w _ 2 w + w =5, M ,⁽₃⁰⁾ + M .(°) 5. w + M .(°) d₂ w + A² I                       i ¹1 ^{13         11 1           12 2} )

^+d 2

n n n __n n I n n n M 23)+M 20) di w + M 20) a 2 w I _ M220)+03+) _ °_), ex f n+1       n     n-1 A / n n nA

^P   7/( l ) ?7/( l )-L7/( l ) -Л A/f( l ) A/f( l W L

—— u _2 u + u   = d. M i 1 _ M u di w +

A ² I ^{1            1         1} i ¹ 1 ^{11          13 1} i

I _ⁿ     _ⁿ      n

+ d₂I M 1 ⁽ 2) _ M 23) 5 , w

nnn

_lM'3_1) + lM33_1) 51 w_ h n , n n o3+) _(-1) o3_) 51 w,

где

u < ^p ) ( t , x ) - J u l ( t , r ) z^p dz ,

_ h

U ^{( r} ) ( t , x ) - J u ( t , r ) Zdz ,

_ h

N

° ij ( t ’ ^r ) = z ® k ° ⁽ j^k ) ( t , ^r ) ,                   ⁽¹⁰⁾

k = 0

to0 = 1 _]T tok,   l = 1,2, 0 < p < M +1, i, j = 1,3, k=1

0 <  r <  L - 2;

* / n + 1       n     n_1 A / n n nA p (.)l) 7,/l)_!_,,(l) —Я    A/f(l)        l) Д _i_ u9 _2u9 + u9   = di Mi _Md? w +

A2 I 2            2         2 I 11      21          13     2 I

I _ⁿ     = n I ⁿ _ⁿ n

+ d₂ I M 22) _ M 23) d ₂ w | _ lM 2 3 ^_1) + lM 33 ^_1) d₂ w _

_ h^l

ⁿⁿ n ⁿ

( R + h ) ¹ о 3 + ) _ ( _1 )'( R — h ) ¹ ° 3 _ ) d₂ w + M 23) ,

0 <  l <  M +1, x e Q, n = 1,2,3,...,

где, согласно (3) и (4),

о j ) , s j ) - тензоры напряжений и деформаций в k -м материале композиции ( k = 0 - связующая матрица, k >  1 - волокна k -го семейства); % _k - параметр упрочнения (Одквиста) в том же материале; U - удельная внутренняя энергия композиции; q i - компоненты вектора осред-ненного теплового потока в композиции, связанные с градиентом температуры законом Фурье для армированной среды (см. (3.1)-(3.3) в [21]); q L± ⁾ - заданные значения тепловых потоков через внешнюю (+) и внутреннюю (-) лицевые поверхности КМ-конструкции. Неизвестные функции u i , S i 3 m ⁾ в соотношениях (1), (2) вычисляются через прогиб w и новые кинематические переменные ui^{(p )}, i = 1,2, 0 <  p <  M + 1 (см. выражения (10)) с помощью матричного равенства (29) из [20], в котором коэффициенты не зависят от решения исследуемой задачи, т.е. вычисляются только один раз.

Производные по времени t в механической составляющей рассматриваемой связанной неизотермической упругопластической задачи аппроксимируем их

P = Р 0 Ю 0 +] E P k ® k , M j ) ( t , x ) ^- J ° ij ( t , r ) zdz , ^k = 1                                 _ h

M ( ) ( t , x ) - J ° R^ zdz , M j ) ( t , x ) - _ h

- J          zdz - lM 33^_" ( t , x ) =