Уточненная модель упругопластического динамического поведения армированных искривленных панелей, чувствительных к скорости деформирования
Автор: Янковский А.П.
Статья в выпуске: 2, 2021 года.
Бесплатный доступ
Сформулирована начально-краевая задача динамического упруговязкопластического деформирования гибких искривленных панелей (пологих оболочек) с «плоско»-перекрестными и пространственными структурами армирования. Неупругое поведение материалов компонентов композиции описывается определяющими уравнениями теории пластического течения с изотропным упрочнением, причем учитывается их чувствительность к скорости деформирования. Геометрическая нелинейность задачи учитывается в приближении Кармана. Используемые кинематические и динамические двумерные соотношения и соответствующие им краевые условия позволяют описывать механическое изгибное поведение пологих композитных оболочек с разной степенью точности. При этом учитывается возможное слабое сопротивление таких армированных панелей поперечным сдвигам. В первом приближении используемые двумерные уравнения, начальные и граничные условия вырождаются в соотношения традиционной неклассической теории Амбарцумяна. Для численного интегрирования поставленной нелинейной динамической задачи применен алгоритм шагов по времени, базирующийся на использовании явной схемы типа «крест». Исследовано упругопластическое и упруговязкопластическое поведение армированных цилиндрических пологих оболочек под действием поперечной динамической нагрузки, порожденной воздушной взрывной волной. Рассматриваются металлокомпозитные и стеклопластиковые тонкостенные конструкции. Продемонстрировано, что отказ от учета зависимости пластических свойств компонентов композиции от скорости их деформирования не позволяет адекватно описывать неупругое динамическое поведение как металлокомпозитных, так и стеклопластиковых пологих оболочек. Показано, что при расчетах даже относительно тонких (с относительной толщиной 1/50) армированных цилиндрических панелей использование теории Амбарцумяна приводит к совершенно неприемлемым результатам по сравнению с уточненной теорией изгиба. Продемонстрировано, что даже для относительно тонких искривленных панелей из стеклопластика замена традиционно используемой «плоско»-перекрестной структуры армирования на пространственную структуру с наклонно уложенными некоторыми семействами волокон позволяет значительно уменьшить не только интенсивность деформаций в связующем материале, но и максимальные по модулю значения прогиба. Для металлокомпозитных пологих оболочек, имеющих слабо выраженную анизотропию композиции, положительный эффект от указанной замены структур армирования практически не проявляется.
Гибкие искривленные панели, пологие оболочки, пространственное армирование, «плоско»-перекрестное армирование, упругопластичность, упруговязкопластичность, чувствительность к скорости деформирования, теория Амбарцумяна, уточненная теория изгиба, динамическое нагружение, численная схема типа «крест»
Короткий адрес: https://sciup.org/146282049
IDR: 146282049 | УДК: 539.4 | DOI: 10.15593/perm.mech/2021.2.17
Текст научной статьи Уточненная модель упругопластического динамического поведения армированных искривленных панелей, чувствительных к скорости деформирования
ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2021PNRPU MECHANICS BULLETIN
Армированные искривленные панели и пологие оболочки широко используются в конструкторской практике [1–12]. Часто такие тонкостенные элементы конструкций из композиционных материалов (КМ) испытывают высокоинтенсивное нагружение [5, 8, 10–14], при котором компоненты композиции могут деформироваться неупруго [5, 10, 12]. При этом адекватность соответствующей механической модели, описывающей такое поведение КМ-конструкций, определяется точностью используемой теории расчета и количеством учитываемых экспериментальных фактов [15–18].
Жесткопластическое и упругопластическое поведение армированных и слоистых пластин моделировалось в [19–21], оболочек с изотропными слоями – в [12], а армированных искривленных панелей – в [22]. В работах [12, 22] использовалась теория пластического течения материалов с изотропным упрочнением. Однако известно, что при интенсивном динамическом нагружении пластические свойства многих материалов зависят от скорости их деформирования [16, 17, 23–25]. (Согласно терминологии, принятой в [26], такое поведение материалов называется упруговязкопластическим.) В связи с этим в [27] была разработана модель упруговязкопластического деформирования армированных гибких пластин.
Возможное слабое сопротивление волокнистых тонкостенных конструкций поперечным сдвигам традиционно описывают в рамках теории Тимошенко – Рейсснера [8, 10, 12, 28], теории Амбарцумяна [27, 29] или Редди – Немировского [4, 9]. Иногда используют теории изгиба более высоких порядков [8, 12, 22, 30], которые базируются, как правило, на гипотезе ломаной линии. В работе [22] было продемонстрировано, что для адекватного описания динамического упругопластического изгибного деформирования пологих КМ-оболочек следует использовать более точную кинематическую модель, чем в теориях Амбарцумяна и Редди – Немировского. Упруговязкопластическое поведение армированных гибких пластин в [27] рассчитывалось по теории Амбарцумяна. В силу этого остался открытым вопрос: нужно ли при расчетах динамики гибких волокнистых конструкций использовать более точные по сравнению с теорией Амбарцумяна теории изгиба в тех случаях, когда компоненты композиции чувствительны к скорости их деформирования?
Для численного интегрирования динамических нелинейных задач механики пластин и оболочек применяют явные схемы, как правило, типа «крест» [12, 22,
27], или же неявные схемы из семейства методов Ньюмарка [5, 31, 32].
В связи с вышеизложенным данная работа посвящена исследованию динамического упруговязкопластического поведения армированных гибких пологих оболочек и искривленных панелей в рамках уточненной теории. Интегрирование соответствующей нелинейной начально-краевой задачи осуществляется с использованием явной численной схемы типа «крест».
1. Постановка задачи
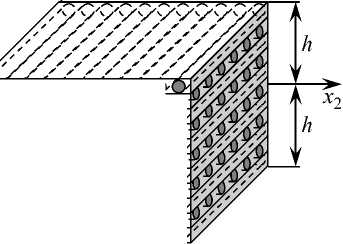
Рассматривается пологая оболочка или искривленная панель, которая имеет толщину 2 h и с которой связана система координат x, так, что поверхность x = 0 -срединная поверхность (| x | < h ), ортогональные линии x и x – линии главной кривизны срединной поверхности, координата x откладывается в поперечном направлении. КМ-конструкция может быть пространственно или традиционно («плоско»-перекрестно) усилена K семействами волокон; плотности армирования k -го семейства волокон обозначим юк (1 < k < K ). По толщине оболочки структура армирования квазиодно-родна. На рис. 1, а изображена ортогональная «плоско»-перекрестная 2D-структура армирования ( K = 2) [33, 34]; на рис. 1, б – пространственная 4D-структура ( K = 4) [34]. Искривленность элементов КМ-панели на рис. 1 не изображена в силу ее малости.
Для описания структуры армирования с k -м семейством арматуры свяжем локальную прямоугольную систему координат x*k ) , причем ось x* к ) сориентируем вдоль волокна, а ее направление зададим двумя углами сферической системы координат 0к и ^ (рис. 2). При этом направляющие косинусы l (к ) между осями x* к ) и Xj ( i , j = 1,3 ) вычисляются по формулам (2.12) из [27].
В [27] было показано, что в случае упруговязкопластического деформирования компонентов композиции при использовании теории изгиба Амбарцумяна явную численную схему типа «крест» для тонкостенных КМ-конструкций можно разработать лишь в частных случаях нагружения и пространственного армирования: на лицевых поверхностях учитываются только нормальные внешние силы; структура пространственного армирования должна обладать следующим свойством: если есть некоторое k -е семейство волокон, уложенное под наклоном (0 < 04 < п / 2), то обязательно должно быть и парное ему l -е семейство, изготовленное из того же материала и имеющее параметры армирования 0; = п — 0А ,
Ф, = Ф4 и ю, = ®к, 1 < k , l < K, l * к (см. рис. 2). Структуры пространственного армирования, обладающие таким свойством, достаточно часто встречаются в инженерной практике [34]. Так, к ним относятся ортогональные 3D-структуры армирования [35, 36], а также структуры, которые изображены на рис. 1. Учитывая эти обстоятельства, в дальнейшем предполагаем, что касательными силами на лицевых поверхностях КМ-конструкции можно пренебречь, а структура укладки волокон отвечает указанному выше требованию. Согласно результатам работы [22] осредненные деформации композиции е и перемещения точек искривленной
КМ-панели U в рамках уточненной теории изгиба ап-
проксимируем так (геометрическую нелинейность
зада-
чи
учитываем в приближении Кармана):
sy (t, r) = "^ (d,и, + 5yu,) — x36(6у w +
^ x m + 1 f h £ 0 h 2 ( m + 1
—
. 2
-4 l(d is^+dj£ ?))+ m + 3
5 ,W 1 „ „
+--+ —5,wd w,
R 2 ‘ j ’
Mm siз (t, r) = (h2 — x32 )E s(m) (t, x), i, j =1,2;
m = 0 h
.x 3
Х 1 ооооооооооо
ООООООООООО
ООООООООООО
ООООООООООО
ООООООООООО
а
ОООООООООО
t x 2
б
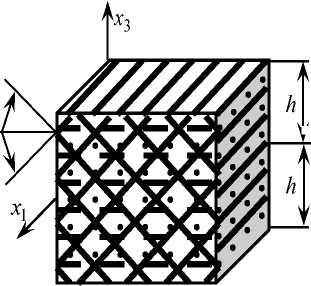
Рис. 1. Элемент искривленной КМ-панели: а – с ортогональной структурой 2D-армирования по эквидистантным поверхностям; б – с пространственной структурой 4D-армирования
Fig. 1. An element of a curved CM-panel: with an orthogonal structure of 2D-reinforcement along equidistant surfaces ( a ); with the spatial structure of 4D-reinforcement ( b )
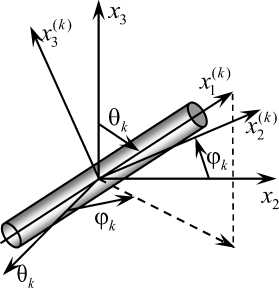
Рис. 2. Локальная прямоугольная система координат, связанная с арматурой k -го семейства
Двумерные уравнения движения элемента гибкой пологой КМ-оболочки в рамках уточненной теории при учете выражений (2), (3) имеют вид [22]
Fig. 2. A local rectangular coordinate system associated with reinforcement of the k -th family
Ut ( t , r ) = ut ( t , x ) - x 3 dz w +
Mm +12 2
+ 2У x|_h---x3_ L(m) (t, x), m?0 h2 (m +1 m + 3 J i3 V } (2)
U3 (t, r) = w(t, x), x gQ, |x3|< h, t > t0, i = 1,2, x = {x, x^}, r = {xx, x^, x3}, где w – прогиб; u – перемещения точек отсчетной поверхности (x3 = 0) в направлениях x ; Rt - главные радиусы кривизны этой поверхности; t – начальный момент времени t; d - оператор частного дифференцирования по координате x (i = 1, 2); M- целое число, задающее количество слагаемых, которые удерживаются в частичных суммах разложений по степеням поперечной координаты x3; Q - область, занимаемая конструкцией в плане. При M = 0 из равенств (1) и (2) получаются кинематические соотношения теорий Амбарцумяна и Редди – Немировского [4, 9, 27, 29]. В выражениях (1), (2) неизвестными являются функции w, ut и 8z(m) (i = 1,2 , 0 < m < M ), зависящие от времени t и только двух пространственных координат x и x .
В настоящей работе исследуется механическое поведение пологой КМ-оболочки как гибкой тонкостенной системы, поэтому напряжение с33 ( t , r ) в поперечном направлении x можно аппроксимировать линейно [27, 28]:
pu(1) = у d, M<1) - M(;) 5,. w - IM(l-1) + lM"-1)5Z w -i Z-^ j ij j3 i i333
j = 1
- h l ^- ( - 1 ) 1 0? ]d w + RT' M^,
2 hp w = У d,( M(0) + У M(0) d, w)-
1 Z—i j 13 Z— js s j=1 V ^=1
-x R- MS0' ■ -=3-), s=1
i = 1,2, 0 < l < M +1, x gQ, t > t0, где p^po ®o +]E pk to k, ®0 = 1 -X ® k, k=1 k=1
M j ) ( t , x )S J a i ( t , r ) x 3 dx 3 , - h
h u"-) (t, x) = j U (t, r) xldx3,
- h h
IM3 l - 1) ( t , x ) = l j a33 ( t , r ) x l - 1 dx3 = (5)
- h
= h - [ ( aM +a 33 ) ( 1 - ( - 1 ) l ) +
+— “(a - + ) -a ( - ) V1 + (- 1 У )! , l + 1V 33 33 ]
i , j = 1Г3, s = 1,2, 0 < l < M + 1;
где p0, pt - объемные плотности материала связующего и арматуры к -го семейства; оу - осредненные напряжения в композиции панели; точка – частная производная по времени t . Массовые силы в (4) не учитываются.
Как и в работе [27], материалы компонентов композиции пологой оболочки предполагаются изотропными и однородными, а их динамическое упруговязкопластическое поведение описывается моделью, которая разработана в [25, 27]. Согласно структурной модели, предложенной в [27], в произвольный момент времени t определяющие уравнения для рассматриваемой композиции можно записать в виде одного матричного равенства
O 33 ( t , r ) =
Q ( + ) ( t , x ) -Q ( 3 ) ( t , x ) 2 h
a = Be+p, где
x 3 +
a 3 ( t , x ) +o 3 - ) ( t , x )
+ 2 ,
x gQ , |x |< h ,
t > t o ,
a = {a 11 , a 22 , a 33 , a 23 , a 31 , a 12 } T ,
6 _ {e 11 , e 22
^ 33 ’ 2 6 23 , 2 б 31 ’ 2 6 12 } ;
где a ( ± ) ( t , x ) = q33 ( t , x , ± h ) - нормальные напряжения
a ,6 - шестикомпонентные векторы-столбцы осред- ненных напряжений оу и деформаций гу в КМ; шести
на нижней (–) и верхней (+) лицевых поверхностях панели, известные из соответствующих силовых граничных условий.
компонентный вектор-столбец p = { pt } и 6 х 6 -матрица
B={*«)
( i , j = 1, 6) вычисляются по матричным фор-
мулам (2.17) из работы [27], причем их элементы зависят от механических характеристик компонентов композиции, от их текущего упруговязкопластического состояния и от структуры армирования (углов 6^, фЛ и плотностей ср (1 < k < K ) армирования); индекс T -операция транспонирования.
Линеаризованное с помощью метода переменных параметров упругости [37] матричное соотношение (6) при учете обозначений (7) представляет собой систему шести алгебраических уравнений. Из третьего равенства этой системы можно выразить
8 33 = b33 ( ° 33 — p 3 — b 31 8 11 — Ь 32 8 22 —
— 2 Ь 34 8 23 — 2 b 35 ^ 31 - 2 b 36 ^ 12 ) , (8)
где производная от напряжения °33 известна после дифференцирования по t аппроксимации (3). Скорости деформаций композиции 8у в правой части (8) получаются путем дифференцирования по времени t кинематических соотношений (1).
Для однозначного интегрирования исследуемой задачи требуется задать граничные и начальные условия. На части кромки КМ-панели (обозначим ее Гс), на которой задаются внешние силы, в рамках уточненной теории изгиба должны выполняться граничные условия в силовых факторах, введенных в (5) [22]:
nx ( M ) — M (3 ) d w ) + n 2 ( M ) — M 23) 8 , w ) = P ( 1 ) ( t , x ) ,
Z n | M p + Z M j8 w | = P ( t , x ) , (9)
j =1 V 1 =1 )
i = 1,2, 0 < 1 < M + 1, x еГа , t > t 0;
на другой части кромки (обозначим ее Гм), на которой задаются перемещения, следует использовать граничные условия для двумерных кинематических величин, которые также введены в (5) [22]:
w(t, х)=U.3 (t, x), u1) (t, x)=u1) (t, x), i = 1,2, 0 < 1 < M +1, x еГ„, t > t0, где
P j1 ) ( t , x )^ ру ( t , r ) x> 3 ,
— h
h u" ’ (t, x) = J U.i (t, r) x^ < j = 1, 3, i = 1, 2), (11)
—h n = cos y, n = sin у;
Pj - внешние силы, приложенные к торцевой поверхности панели; U^ - прогиб, который известен на Гм; U*. - заданные перемещения точек торцевой поверхности в тангенциальных направлениях x ( г = 1,2 ); у -угол, который определяет направление внешней нормали к контуру Г = Г U Г , ограничивающему область Q .
Начальные условия при t = t0 имеют вид (см. соотношения (2) и (5)) [22]
w ( t 0 , x ) = U 03 ( x ) , w ( t 0 , x ) = V 03 ( x ) , u 1 ) ( t 0 , x ) = “ 0? ( x ) ,
U1) (10, x) = ^011 (x), x €Q i = 1,2, 0 < 1 < M +1, где ui’ (x) H J и0i (r)x3dx3, v0') (x) h J Vi (r)x3dx3,
— h — h ( 3)
i = 1,2, 0 < 1 < M + 1;
Uoj , V y ( j = 1,3) - известные в начальный момент времени t перемещения и скорости точек пологой КМ-оболочки.
Неизвестные двумерные функции w, u. и 8 < m ) (0 < m < M ), которые использованы в выражениях (1) и (2), и введенные соотношениями (5) кинематические переменные u < 1 ) ( г = 1, 2 , 0 < 1 < M + 1) связаны матричным равенством (27) из работы [22], элементы матрицы которого не зависят от решения рассматриваемой задачи.
2. Метод расчета
Как уже отмечалось, численное решение исследуемой задачи будем строить на базе алгоритма шагов по времени [5, 12, 22, 27, 31, 32, 37], поэтому неизвестные функции будем определять в дискретные моменты времени tn^ j = tn + т ( n = 0,1, 2...), где т = const > 0 - шаг по времени. Согласно результатам работ [22, 27] считаем, что при t = tm уже известны значения следующих величин:
w ( x ) H w ( t m , x ) , u S ) ( x ) H US * ) ( t m , x ) ,
CT m )('x') = a( ± 4t X 1 d m )('x1 = d< ± 4t xl
U33 (x) H U33 (tm , x) , U33 (x) — U33 (tm , x) , mm
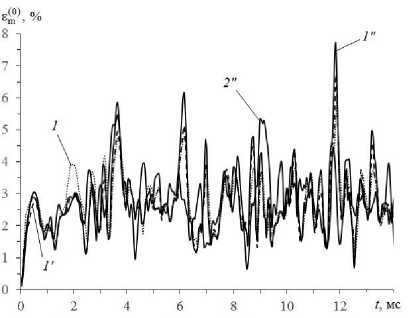
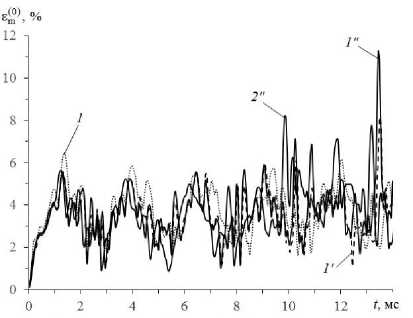
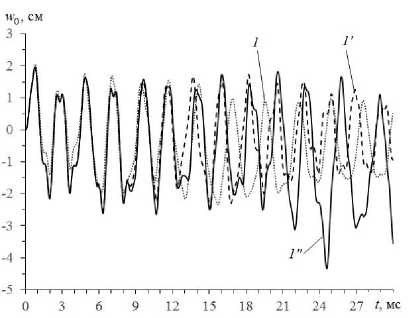
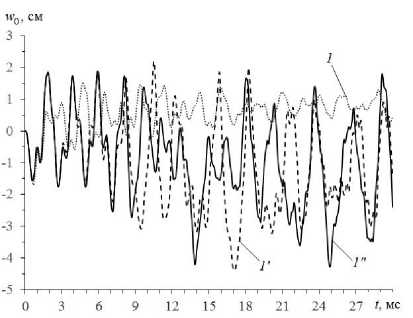
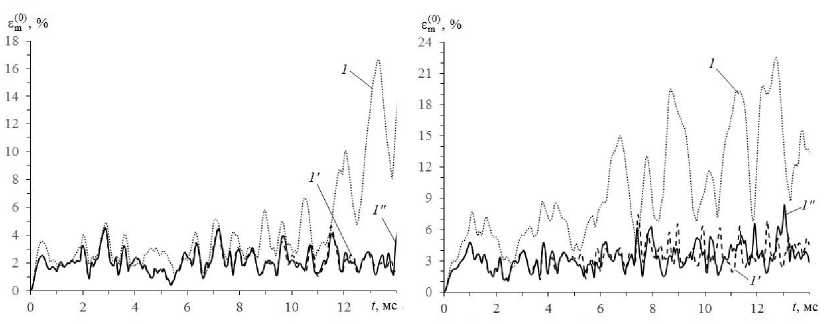
° j ( r ) H ° j ( tm , r ) , ® 8 < k )(r] = 8< k )(t 8< k 4a = 8< kHt 8ij (r )h8 ij (tm , 1 ) , 8 ij (r )H8ij (tn—1, r ) , ё—Чг^^k )(t r ) vmk )(r} = p-k 4tri 8 ij (r )H8ij (tn—1, r ) , x (r )hX (tm , r ) , s = 1, 2, i, j = 1,3, m = n — 1, n, 0 < 1 < M +1, 0 < k < K, x eQ, |x |< h, где ° Производные по времени далее аппроксимируем центральными конечными разностями на шаблоне {tn_j, tn, tn+J [22, 27] (исключение при этом составляют лишь случаи, которые оговорены формулами (2.8), (2.9) в работе [27]). Это позволяет разработать явную численную схему для интегрирования рассматриваемой начально-краевой задачи. Заменим вторые производные по времени в левых частях соотношений (4) их конечноразностными аналогами, тогда при учете обозначений, аналогичных (14), будем иметь Необходимые условия устойчивости построенной численной схемы типа «крест» вытекают из критерия Куранта и для однородных пластин и оболочек указаны в [12]. При выполнении этих условий для каждого материала композиции соответствующие условия устойчивости заведомо выполняются с запасом и для искривленной КМ-панели [22, 27]. 3. Обсуждение результатов расчетов 2 ho (n+1 n n—1 —— I w - 2 w + w т V n -Ya, m(0)+Ym(0) a, w -j j3 ji i 2 n nn Y R-1 Л/(°) -I- rV+)<-/-) -^ Ri M, + ’33 -’33 , i=1 _ ( n+1 n n-1 A 2 ( n n P| „ —I u - 2 ui + ui I-^aj I Mj -Mj з о iw I- т V ) j-1 V7 n n n - h ’(+) -(-1)1 °-) 5, w- lM„l-1) + +lMd3-1)d, w+ R1 MR, x eQ, i -1,2, 0 < l< M +1, n -1,2,3,... Рассмотрим упруговязкопластическое и упругопластическое динамическое изгибное деформирование относительно тонких цилиндрических КМ-панелей толщиной 2h - 2 см, занимающих в плане прямоугольную область Q : X|< a , |x2|< b (а - 3b , b - 50 см , h / b -1/50). Пологие оболочки имеют искривление в направлении х2(1 / R - 0 , R - const) со стрелой подъема f -12 см. Радиус кривизны срединной поверхности при этом определяется так [22]: R - (b2+ f2) / (2 f), 0 < f< 0,4b . По всей кромке Г-Гмпанели жестко закреплены (см. (10) и (11) при U^ = 0) и до момента времени t -10- 0 находятся в естественном состоянии (см. (12) и (13) при учете UOz= 0 и VOi = 0 , i -1,3). Конструкции нагружаются давлением p (t), которое порождается воздушной взрывной волной (см. (3), (4) и (15)) [31]: Согласно (5) и (14) правые части в (15) известны, поэтому после добавления к уравнениям (15) необходимых граничных условий (9), (10) при учете (11) можем по явной численной схеме рассчитать значения n+1 n+1 функций w и u(l) (0 < l< M +1) в момент времени tn+j. Далее по матричной формуле (30) из работы [22] опреде-n+1 n+ 1 ляем искомые функции u. и £(m) (i -1, 2 , 0 < m < M), затем на основании выражений (1) вычисляем осред-n+1 ненные деформации композиции пологой оболочки £„ . После этого решение исследуемой задачи при учете соотношений (6) и (8) строится совершенно так же, как и в работах [22, 27]. Структура левых частей равенств (15) свидетельствует о том, что для начала расчета по разработанной численной схеме необходимо предварительно опреде-0 0(l) лить значения функций w , u (они заданы начальны- ■-)('>-{-.p('), °- (' Hp ('), Рmax > 0, Рmax < 0, Рmax > 0, Рmax < 0, Р(')- p tit . 0 Р max max, i _Рmax exP [-«■(' - 'max )] , max , ’ ' > 'max , a-- ln(0,01)/ ( 'min - 'max )> 0, t »t . min max . В соотношениях (16) смысл параметров Ртах, 'тах и tminвполне очевиден и подробно описан в [22]. Согласно выражениям (16) в случае Ртах > 0 динамическое давление прикладывается к нижней (вогнутой) лицевой поверхности, а в случае Ртах< 0 - к верхней (выпуклой) лицевой поверхности. На основании экспериментальных данных [31] в дальнейших расчетах примем 'max - 0,1 мс и 'min - 2 мс . Пологие КМ-оболочки изготовлены из эпоксисвязующего [38], армированного стекловолокнами [33] (стеклопластик), или из магниевого сплава ВМ65 [23], усиленного стальной проволокой У8А [33] (металло-композиция). Упругопластическое деформирование материалов композиций при фиксированной скорости деформации характеризуется диаграммой растяжения -сжатия: ' E(k) e, |e| c = S sign (e)o( k) + Es k) (e-sign (e)eS k)), |e|>eS k), 0 < k < K, где a, e - осевое напряжение и соответствующая деформация; E(k), Esk) = Es(k) (E) - модули упругости и упрочнения k-го компонента композиции; a(k) = a(k) (Е) -предел текучести того же компонента при скорости деформации Е = const. Физико-механические характеристики материалов композиции приведены в таблице, где v - коэффициент Пуассона. (Аппроксимации зависимостей a(k) (Е), E(k) (E) по данным, представленным в таблице, подробно обсуждаются в [27].) Физико-механические характеристики материалов композиций [23, 33, 38] Physical and mechanical characteristics of materials of compositions [23, 33, 38] Материал Е, c 1 р, кг / м3 E, ГПа ν a, МПа Es, ГПа Эпоксидная смола 5 • 10-4 104,0 1210 2,8 0,33 20 22 1,114 1,238 Стеклянные волокна 5 • 10-4 104,0 2520 86,8 0,25 4500 4600 6,230 6,314 Магниевый 5 • 10-4 267 0,379 сплав 0,417 1800 43,0 0,33 306 0,589 ВМ65 (Mg) 104,0 385 1,010 Стальная проволока У8А 5 • 10-4 104,0 7800 210,0 0,31 3968 4100 6,973 7,035 Исследуется динамическое поведение КМ-панелей с двумя однородными (^ = const, 0^ = const и Ф^ = const) структурами армирования: 1) традиционное армирование в двух (K = 2) ортогональных направлениях, когда два семейства волокон укладываются по эквидистантным поверхностям в направлениях x , x с плотностями армирования ^ = ю2= 0,2 (см. рис. 1, а); 2) пространственное 4D-армирование (K = 4), когда первые два семейства волокон по-прежнему укладываются в направлениях x , x , а третье и четвертое семейства – наклонно по направлениям, задаваемым углами (см. рис. 2): 03= п /4, 04= 3п /4 и ф3= ф4= п /2 (см. рис. 1, б при 0 = п /4). Плотности армирования в последнем случае имеют значения: ^ = 0,1, ю2= 0,2 и ю3= ю4= 0,05 . В обеих структурах армирования общий расход волокон одинаков. На рис. 3 изображены осцилляции прогиба центральных точек (w0 (t) = w(t, 0, 0)) стеклопластиковых пологих оболочек при |pmaх| = 6 МПа; на рис. 4 - осцилляции наибольших значений интенсивности деформаций связующей матрицы e(0) (E(0) (t ) = max e(0) (t, r), |x | < a , |x1 < b и |x | < h) тех же КМ-панелей; на рис. 5 и 6 представлены аналогичные зависимости w0 (t) и Е^) (t), рассчитанные для Мд-У8А-конструкций при IРтах | = 20 МПа. Номера кривых на рис. 3-6 соответствуют номерам структур армирования. Кривые 1 и 1′ рассчитаны по теории Амбарцумяна (M = 0), а кривые 1” и 2” - по уточненной теории изгиба при M = 7 (см. (1) и (2)). Штриховые кривые 1′ и сплошные кривые 1″ и 2″ получены при учете чувствительности материалов композиций к скорости их деформирования; пунктирные кривые 1 определены без учета этой чувствительности (упругопластический расчет). В последнем случае были использованы механические характеристики материалов, соответствующие скорости деформирования Е = 5 -10"4c-1 (см. таблицу). Кривые на рис. 3, а -рис. 6, а соответствуют случаям pmaх > 0 , т.е. нагружению КМ-панелей со стороны нижних (вогнутых) лицевых поверхностей; на рис. 3, б - 6, б - случаям pmaх< 0, т.е. нагружению со стороны верхних (выпуклых) лицевых поверхностей. а б Рис. 3. Прогибы центральных точек пологих цилиндрических оболочек из стеклопластика, рассчитанные по разным теориям при нагружении конструкций снизу (а) и сверху (б) Fig. 3. Deflections of the central points of shallow cylindrical shells made of fiberglass, calculated according to different theories when the structures are loaded from below (a) and from above (b) Рис. 4. Максимальные значения интенсивности деформаций связующего материала искривленных панелей из стеклопластика, рассчитанные по разным теориям при нагружении конструкций снизу (а) и сверху (б) б Fig. 4. Maximum values of the intensity of deformations of the binder material of curved fiberglass panels, calculated according to different theories under loading of structures from below (a) and from above (b) Рис. 5. Прогибы центральных точек пологих цилиндрических оболочек из Mg–У8А-композиции, рассчитанные по разным теориям при нагружении конструкций снизу (а) и сверху (б) б Fig. 5. Deflections of the central points of shallow cylindrical shells made of Mg–U8A-composition, calculated according to different theories under loading of structures from below (a) and from above (b) б а Рис. 6. Максимальные значения интенсивности деформаций связующего материала искривленных панелей из Mg–У8А-композиции, рассчитанные по разным теориям при нагружении конструкций снизу (а) и сверху (б) Fig. 6. Maximum values of the intensity of deformations of the binder material of curved panels made of Mg-U8A-composition, calculated according to different theories when the structures are loaded from below (a) and from above (b) Сопоставление кривых 1 и 1′ на рис. 3 и 4 свидетельствует о том, что даже в случае относительно тонких стеклопластиковых панелей, материалы композиции которых имеют слабую зависимость пластических свойств от скорости их деформирования, расчет, выполненный без учета этой зависимости, приводит к неадекватным результатам. Еще большая разность в поведении кривых 1 и 1′ просматривается на рис. 5 и 6, т.е. в случаях металлокомпозитных панелей, связующий материал которых проявляет значительную чувствительность пластических свойств к изменению скорости его деформирования (см. таблицу). Следует отметить, что различие кривых 1 и 1′ в большей степени наблюдается на рис. 3, б – рис. 6, б (чем на рис. 3, а – рис. 6, а), т.е. при нагружении КМ-панелей сверху (со стороны выпуклых лицевых поверхностей). Таким образом, для получения адекватных результатов динамических расчетов неупругого поведения даже относительно тонких искривленных КМ-панелей нужно учитывать чувствительность материалов композиции к скорости их деформирования, причем даже в тех случаях, когда такая чувствительность слабо выражена. Сравнение штриховых кривых 1′ и сплошных кривых 1″ на рис. 3–6 показывает, что эти кривые существенно различаются как для стеклопластиковых КМ-панелей (рис. 3 и 4), материалы композиции которых слабо чувствительны к скорости их деформирования, так и металлокомпозитных пологих оболочек (рис. 5 и 6), связующее которых сильно чувствительно к изменению скорости его деформирования. При этом значительное различие кривых 1′ и 1″ наблюдается как при сравнении прогибов (рис. 3 и 5), так и при сопоставлении интесивности деформаций в связующей матрице (рис. 4 и 6). Следовательно, для проведения адекватных динамических расчетов упруговязкопластического поведения пологих КМ-оболочек целесообразно использовать уточненные (по сравнению с традиционной неклассической теорией Амбарцумяна) теории изгиба тонкостенных элементов конструкций. В связи с этим далее будем проводить сравнение расчетов, выполненных по уточненной теории при M = 7 (см. (1) и (2)). Сопоставление кривых 1″ и 2″ на рис. 3 и 4 демонстрирует, что замена традиционной 2D-структуры армирования 1 (см. рис. 1, а) на пространственную 4D-структуру 2 (см. рис. 1, б) даже в случае относительно тонких панелей из стеклопластика позволяет существенно уменьшить как максимальные по модулю значения прогибов центральных точек рассматриваемых пологих оболочек (см. рис. 3), так и наибольшие значения интенсивности деформаций эпоксисвязующего (см. рис. 4). Следовательно, даже в случаях относительно тонких искривленных панелей из стеклопластика, когда анизотропия композиции сильно выражена, замена традиционной ортогонально-перекрестной 2D-структуры армирования 1 на пространственную 4D-структуру армирования 2 позволяет существенно уменьшить максимальные прогибы пологой оболочки и наибольшие значения интенсивности деформаций связующего при упруговязкопластическом деформировании таких КМ-конструкций. Кривые 2″ на рис. 5 и 6 не изображены, чтобы их не загромождать. Соответствующие расчеты показали, что в случае относительно тонких металлокомпозитных искривленных панелей, композиции которых имеют слабо выраженную анизотропию, указанная выше замена структур армирования позволят незначительно уменьшить максимальное значение интенсивности деформаций связующего материала, но не приводит к уменьшению максимального по модулю значения прогиба. Таким образом, в металлокомпозитных пологих оболочках «жесткая» связующая матрица достаточно хорошо сопротивляется при изгибе поперечному сдвигу, поэтому замена «плоско»-перекретной укладки арматуры на пространственную 4D-структуру армирования в относительно тонких КМ-конструкциях не приводит к заметному положительному эффекту. Согласно же результатам, полученным в [27], в относительно толстых (с относительной толщиной 1/10) металлокомпозитных пластинах такой эффект проявляется весьма ярко. Заключение Построенная уточненная модель неупругого динамического изгибного деформирования пологих КМ-оболочек позволят более точно (по сравнению с традиционной неклассической теорией Амбарцумяна) определять неупругое поведение таких армированных элементов тонкостенных конструкций при учете чувствительности материалов композиции к скорости их деформирования. Проведенные расчеты упругопластического и упруговязкопластического поведения динамически нагружаемых в поперечном направлении искривленных КМ-панелей показали, что даже для относительно тонких конструкций неучет чувствительности компонентов композиции к скорости их деформирования дает совершенно неприемлемые результаты как для металлокомпозитных изделий (материалы которых сильно чувствительны к изменению скорости их деформирования), так и для стеклопластиковых пологих оболочек (компоненты которых слабо чувствительны к такому изменению). Особо ярко этот неучет проявляется при расчетах динамического поведения металлокомпозитных искривленных панелей. Кроме того, выявлено, что результаты расчетов упруговязкопластического поведения даже относительно тонких пологих КМ-оболочек, выполненных (расчетов) по теории Амбарцумяна и по уточненной теории изгиба существенно различаются как при определении прогибов конструкции, так и при определении деформированного состояния компонентов композиции. Сле- довательно, для проведения адекватных динамических расчетов упруговязкопластического деформирования искривленных армированных панелей необходимо использовать уточненную теорию их изгиба, а не простейшую неклассическую теорию Амбарцумяна. Продемонстрировано, что в случае пологих оболочек положительный эффект от замены «плоско»-перекрестной структуры армирования, которая традиционно используется в таких КМ-изделиях [33] (см. рис. 1, а), на пространственную структуру 4D-армирования [34] (см. рис. 1, б) проявляется не только в относительно толстых панелях (с относительной толщиной 1/10 [27]), но и в относительно тонких конструкциях (с относительной толщиной 1/50). Причем в последнем случае удается не только уменьшить максимальные значения интенсивности деформаций связующей матрицы, но и значительно уменьшить проги- бы искривленной панели. Эффективность указанной замены структур армирования проявляется тем больше, чем сильнее выражена анизотропия КМ-изделия. В силу этого данный эффект ярко проявляется, например, в стеклопластиковых панелях и значительно слабее в металлокомпозитных.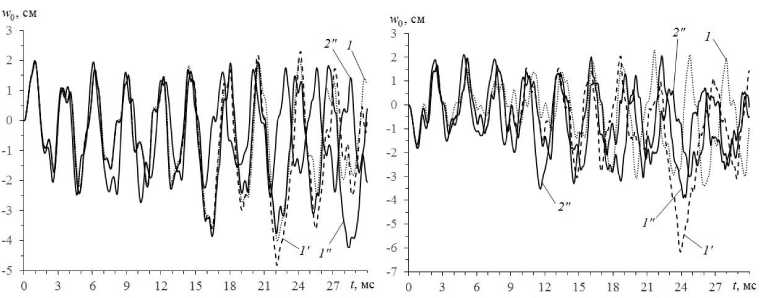
Список литературы Уточненная модель упругопластического динамического поведения армированных искривленных панелей, чувствительных к скорости деформирования
- Review of advanced composite structures for naval ships and submarines / A.P. Mouritz, E. Gellert, P. Burchill, K. Challis // Compos. Struct. - 2001. - Vol. 53, no. 1. - P. 21-42.
- Bannister M. Challenger for composites into the next millennium - a reinforcement perspective // Composites. - 2001. -Part A 32. - P. 901-910.
- Soutis C. Fibre reinforced composites in aircraft construction // Progress in Aerospace Sciences. - 2005. - Vol. 41, no. 2. -P. 143-151.
- Reddy J.N. Mechanics of laminated composite plates and shells: Theory and analysis / 2nd ed. - Boca Raton: CRC Press, 2004. - 831 p.
- Kazanci Z. Dynamic response of composite sandwich plates subjected to time-dependent pressure pulses // International Journal of Non-Linear Mechanics. - 2011. - Vol. 46. - P. 807-817.
- Gibson R.F. Principles of composite material mechanics / 4rd ed. - Boca Raton: CRC Press, Taylor & Francis Group, 2015. - 815 p.
- Gill S.K., Gupta M., Satsangi P. Prediction of cutting forces in machining of unidirectional glass-fiber-reinforced plastic composites // Frontiers of Mechanical Eng. - 2013. - Vol. 8, no. 2. - P. 187-200.
- Vasiliev V.V., Morozov E. Advanced mechanics of composite materials and structural elements. - Amsterdam: Elsever, 2013. - 412 p.
- Андреев А. Упругость и термоупругость слоистых композитных оболочек. Математическая модель и некоторые аспекты численного анализа. - Saarbrucken (Deutschland): Pal-marium Academic Publishing, 2013. - 93 c.
- Прикладные задачи механики цилиндрических оболочек / Ю.С. Соломонов, В.П. Георгиевский, А.Я. Недбай, В.А. Андрюшин. - М.: Физматлит, 2014. - 408 с.
- Димитриенко Ю.И. Механика композитных конструкций при высоких температурах. - М.: Физматлит, 2019. - 448 с.
- Абросимов Н.А., Баженов В.Г. Нелинейные задачи динамики композитных конструкций. - Н. Новгород: Изд-во ННГУ, 2002. - 400 с.
- Qatu M.S, Sullivan R.W., Wang W. Recent research advances on the dynamic analysis of composite shells: 2000-2009 // Composite Structures. - 2010. - Vol. 93. - P. 14-31.
- Alderliesten R.C., Benedictus R. Modelling of impact damage and dynamics in fibre-metal laminates - A review // Int. J. Impact Eng. - 2014. - Vol. 67. - P. 27-38.
- Malachowsky J., L'vov G., Daryazadeh S. Numerical prediction of the parameters of a yield criterion for fibrous composites // Mech. Compos. Mater. - 2017. - Vol. 53, no. 5. - P. 589-600.
- Hajlane A., Varna J. Identification of a model of transverse viscoplastic deformation for a ud composite from curvature changes of unsymmetric cross-ply specimens // Mech. Compos. Mater. - 2019. - Vol. 55, no. 3. - P. 519-552.
- Effect of degree of cure on viscoplastic shear strain development in layers of [45/-45]s glass fibre/epoxy resin composites / L. Pupure, S. Saseendran, J. Varna, M. Basso // J. Compos. Mater. - 2018. - Vol. 52, no. 24. - P. 3277-3288.
- Fedotov A.E. Hybrid model for homogenization of the elastoplastic properties of isotropic matrix composites // Mech. Compos. Mater. - 2017. - Vol. 53, no. 3. - P. 361-372.
- Jahangirov A. Load-carrying capacity of fiber-reinforced annular tree-layer composite plate clamped on its external and internal contours // Mech. Compos. Mater. - 2016. - Vol. 52, no. 2. - P. 271-280.
- Romanova T.P. Modeling the dynamic bending of rigid-plastic hybrid composite curvilinear plates with rigid inclusion // Mech. Solids. - 2019. - Vol. 54, no. 5. - P. 134-150.
- Starovoitov E.I., Leonenko D.V. Deformation of an elas-toplastic circular three-layer plate in temperature field // Mech. Compos. Mater. - 2019. - Vol. 55, no. 4. - P. 727-740.
- Янковский А.П. Уточненная модель упругопластиче-ского изгибного деформирования гибких армированных пологих оболочек, построенная на основе явной схемы типа «крест» // Вычислительная механика сплошных сред. - 2017. -Т. 10, № 3. - С. 276-292.
- Расчеты на прочность, устойчивость и колебания в условиях высоких температур / Н.И. Безухов, В.Л. Бажанов, И.И. Гольденблат, Н.А. Николаенко, А.М. Синюков; под ред. И.И. Гольденблата. - М.: Машиностроение, 1965. - 567 с.
- Белл Дж. Экспериментальные основы механики деформируемых твердых тел. Часть II. Конечные деформации. -М.: Мир, 1984. - 431 с.
- Каримбаев Т.Д., Мамаев Ш. Модель упругопласти-ческого течения при переменной скорости деформирования // Вестник Нижегород. ун-та им. Н.И. Лобачевского. Механика. - 2013. - № 5 (1). - С. 179-187.
- Коларов Д., Балтов А., Бончева Н. Механика пластических сред. - М.: Мир, 1979. - 302 с.
- Янковский А.П. Моделирование упругопластическо-го изгиба пространственно-армированных пластин при учете чувствительности компонентов композиции к изменению скорости деформирования // Прикладная математика и механика. - 2019. - Т. 83, № 4. - С. 660-686.
- Богданович А.Е. Нелинейные задачи динамики цилиндрических композитных оболочек. - Рига: Зинатне, 1987. - 295 с.
- Амбарцумян С.А. Общая теория анизотропных оболочек. - М.: Наука, 1974. - 446 с.
- Whitney J., Sun C. A higher order theory for extensional motion of laminated composites // J. of Sound and Vibration. -1973. - Vol. 30, no. 1. - P. 85-97.
- Houlston R., DesRochers C.G. Nonlinear structural response of ship panels subjected to air blast loading // Computers & Structures. - 1987. - Vol. 26, no. 1/2. - P. 1-15.
- Zeinkiewicz O.C., Taylor R.L. The finite element method. - Oxford: Butterworth-Heinemann, 2000. - 707 p.
- Композиционные материалы: справочник / под ред. Д.М. Карпиноса. - Киев: Наук. думка, 1985. - 592 с.
- Тарнопольский Ю.М., Жигун И.Г., Поляков В.А. Пространственно-армированные композиционные материалы: справочник. - М.: Машиностроение, 1987. - 224 с.
- Композиционные материалы, армированные системой прямых взаимно ортогональных волокон. 2. Экспериментальное изучение / И.Г. Жигун, М.И. Душин, В.А. Поляков, В.А. Якушин // Механика полимеров. - 1973. - № 6. - С. 1011-1018.
- Schuster J., Heider D., Sharp K., Glowania M. Measuring and modeling the thermal conductivities of three-dimensionally woven fabric composites // Mechanics of Composite Materials. - 2009. - Vol. 45, no. 2. - P. 241-254.
- Хажинский Г.М. Модели деформирования и разрушения металлов. - М: Научный мир, 2011. - 231 с.
- Справочник по композитным материалам: в 2 кн. Кн. 1 / под ред. Дж. Любина; пер. с англ. А.Б. Геллера, М.М. Гельмонта; под ред. Б.Э. Геллера. - М.: Машиностроение, 1988. - 448 с.


