Уточненная модель вязкоупругопластического деформирования армированных цилиндрических оболочек
Автор: Янковский А.П.
Статья в выпуске: 1, 2020 года.
Бесплатный доступ
Сформулирована начально-краевая задача вязкоупругопластического изгибного поведения цилиндрических круговых оболочек, перекрестно армированных по эквидистантным поверхностям. Мгновенное упругопластическое деформирование компонентов композиции оболочек описывается определяющими уравнениями теории пластического течения с изотропным упрочнением. Вязкоупругое деформирование этих материалов описывается определяющими соотношениями модели тела Максвелла - Больцмана. Геометрическая нелинейность задачи учитывается в приближении Кармана. Используемая система двумерных разрешающих уравнений и соответствующие им начальные и граничные условия позволяют с разной степенью точности определять перемещения и напряженно-деформированное состояние (в том числе остаточные) в материалах композиции гибких цилиндрических оболочек. При этом учитывается слабое сопротивление рассматриваемых композитных конструкций поперечным сдвигам. В первом приближении использованные уравнения, начальные и граничные условия соответствуют соотношениям широко применяемой неклассической теории Редди. Численное решение поставленной начально-краевой задачи строится с использованием явной пошаговой схемы типа «крест». Исследовано упругопластическое и вязкоупругопластическое динамическое деформирование относительно тонкой длинной круговой цилиндрической оболочки. Конструкция рационально армирована в окружном направлении и нагружена внутренним давлением взрывного типа. Продемонстрировано, что при интенсивном кратковременном нагружении даже относительно тонкой цилиндрической армированной оболочки внутренним давлением традиционная теория Редди не гарантирует получения величины максимума остаточного прогиба и интенсивности остаточных деформаций компонентов композиции с точностью до 10 % по сравнению с расчетами, выполненными по уточненной теории. Различие в результатах соответствующих расчетов возрастает с увеличением относительной толщины композитной конструкции. Обнаружено, что после пластического деформирования длинной армированной цилиндрической оболочки в ее остаточном состоянии проявляются не только зоны краевых эффектов, но и локальная зона интенсивного деформирования, расположенная в окрестности центрального сечения конструкции. Протяженность локальной центральной зоны сопоставима с протяженностью зон краевых эффектов. Показано, что амплитуда поперечных колебаний армированной оболочки в окрестности начального момента времени существенно (на порядок) превышает величину максимального по модулю остаточного прогиба. Поэтому расчеты, выполненные в рамках теории упругопластического деформирования материалов композиции, не позволяют даже весьма приближенно оценить величины остаточных перемещений и остаточного деформированного состояния компонентов композиции цилиндрической оболочки при ее динамическом нагружении.
Цилиндрические оболочки, эквидистантное армирование, вязкоупругопластическое деформирование, геометрическая нелинейность, динамическое нагружение взрывного типа, теория редди, уточненные теории деформирования оболочек, модель тела максвелла - больцмана, теория пластического течения, явная численная схема
Короткий адрес: https://sciup.org/146281976
IDR: 146281976 | УДК: 539.4 | DOI: 10.15593/perm.mech/2020.1.11
The refined model of viscoelastic-plastic deformation of reinforced cylindrical shells
The paper formulates the initial-boundary-value problem of the viscoelastic-plastic bending behavior of cylindrical circular shells cross-reinforced along equidistant surfaces. The instant elastoplastic deformation of the shell composition components is described by the governing equations of the theory of plastic flow with isotropic hardening. The viscoelastic deformation of these materials is described by the defining relations of the Maxwell - Boltzmann model of body. The geometric nonlinearity of the problem is taken into account in the Karman approximation. The used system of two-dimensional resolving equations and the corresponding initial and boundary conditions make it possible to determine displacements and stress-strain state (including residual one) in materials of the composition of flexible cylindrical shells with varying degrees of accuracy. In this case, the weak resistance of the considered composite structures to transverse shears is taken into account. In the first approximation, the equations are used, the initial and boundary conditions correspond to the relations of the widely used non-classical Reddy theory. A numerical solution of the initial-boundary-value problem posed is constructed using an explicit step-by-step "cross" scheme. The elastoplastic and viscoelastic-plastic dynamic deformation of a relatively thin long circular cylindrical shell is investigated. The structure is rationally reinforced in the circumferential direction and is loaded with an internal pressure of an explosive type. It has been demonstrated that under intense short-term loading even of a relatively thin cylindrical reinforced shell by internal pressure, the traditional Reddy theory does not guarantee that the maximum residual deflection and the intensity of residual deformations of the components of the composition are accurate to within 10% compared to calculations performed by the refined theory. The difference in the results of the corresponding calculations increases with an increase in the relative thickness of the composite shell. It was found that after plastic deformation of a long reinforced cylindrical shell in its residual state, not only appear zones of edge effects, but also a local zone of an intense deformation located in the vicinity of the central section of the shell. The length of the local central zone is comparable with the length of the zones of edge effects. It is shown that the amplitude of the transverse vibrations of the reinforced shell in the vicinity of the initial moment of time significantly (by an order of magnitude) exceeds the value of the maximum modulus of the residual deflection. Therefore, the calculations performed in the framework of the theory of elastoplastic deformation of composition materials do not allow a very approximate determination of the magnitude of the residual displacements and the magnitude of the residual deformed state of the components of the composition of the cylindrical shell.
Текст научной статьи Уточненная модель вязкоупругопластического деформирования армированных цилиндрических оболочек
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2020PNRPU MECHANICS BULLETIN
Цилиндрические оболочки из композиционных материалов (КМ) широко используются в инженерных приложениях в качестве тонкостенных силовых элементов [1-5]. Поэтому актуальной является проблема математического описания механического поведения таких оболочек, особенно при воздействии высокоинтенсивных динамических нагрузок [5].
В рамках классической теории деформирования слоистые и анизотропные оболочки изучались в [6-8], но при этом игнорируется экспериментально уста -новленный факт слабого сопротивления КМ-оболочек поперечным сдвигам, которые традиционно учитываются в рамках теории Рейсснера - Миндлина [5, 9-14] или теории Редди [7, 15-18], реже используются теории более высоких порядков точности [19-23]. При этом в подавляющем большинстве публикаций рассматривается линейно-упругое или линейно-вязкоупругое деформирование тонкостенных конструкций из КМ [5-7, 911, 13-17, 19-22]. Однако известно, что компоненты композиции могут деформироваться и пластически [4, 8, 18, 23-26]. Проблема моделирования неупругого поведения КМ-конструкций при высокоинтенсивных нагрузках находится сейчас на стадии становления. Так, в [8] исследовалось предельное состояние армированных цилиндрических оболочек на базе модели жесткопластического деформирования компонентов композиции; в [12] изучалось динамическое упругопластическое поведение слоистых тонкостенных конструкций с изотропными слоями; в [23] моделировалось упругопластическое деформирование волокнистых цилиндрических оболочек. Ранее в [15] было продемонстрировано, что при линейно -упругом деформировании компонентов композиции оболочек не требуется уточнять результаты расчетов, выполненные по теории Редди. Но в [23] показано, что для адекватного описания динамического неупругого поведения армированных цилиндрических оболочек необходимо использовать более точные, чем теория Редди, модели деформирования таких тонкостенных элементов КМ-конструкций.
Механическое поведение материалов композиции в [12, 23] описывалось определяющими соотношениями теории Прандтля – Рейсса – Хилла (ТПРХ) [27], в которых не учитываются демпфирующие свойства реальных материалов при осциллирующем деформировании [28]. Следовательно, модели, использованные в [12, 23], не позволяют рассчитывать остаточные перемещения и остаточное напряженно-деформированное состояние (НДС) в компонентах композиции при интенсивных динамических воздействиях на КМ-оболочки. Демпфирующие свойства материалов композиции волокнистых пластин учтены в [18], где была разработана структурная модель вязкоупругопластического поведения перекрестно армированного по эквидистантным поверхностям тонкостенного КМ-элемента.
Для численного решения динамических задач механики тонкостенных элементов КМ-конструкций используют явные схемы, например типа «крест» [12, 18, 23], или неявные методы, как правило, Ньюмарка [29–32].
В связи с вышеизложенным настоящее исследование посвящено математическому моделированию вязкоупругопластического поведения гибких цилиндрических волокнистых оболочек в рамках уточненной теории их изгиба при использовании явной численной схемы типа «крест».
1. Постановка задачи
Рассмотрим тонкую замкнутую круговую цилиндрическую оболочку радиусом R , длиной L и толщиной 2 h <$cmin ( L, R ) (рис. 1), с которой связана цилиндрическая система координат x , где x – осевая координата (0 < x < L ), x2 - угловая окружная координата (0 < x < 2 п ), x - радиальная координата ( R — h < x < R + h ). Оболочка усилена N семействами волокон с плотностями юк и углами ^к (1 < k < N ) армирования, отсчитываемыми от направления x . Волокна уложены по поверхностям, эквидистантным срединной поверхности конструкции ( x3 = const), и структура армирования однородна в радиальном направлении.
Как и в [23], ограничимся исследованием практически важного частного случая, когда на лицевых поверх- ностях оболочки можно пренебречь действием касательных внешних распределенных сил. Согласно этому предположению для учета слабого сопротивления рассматриваемой КМ-оболочки поперечным сдвигам аппроксимируем усредненные деформации композиции гу и перемещения U. точек конструкции следующими соотношениями [23] (геометрическая нелинейность задачи учитывается в приближении Кармана):
2 — т2 KLf
6з ( t , r ) = —тт- Е [т|е (3) ( t , x ) , h 3 = 0 V h )
x = { x , x 2} , r = { x , x 2, x 3} , x3 = R + z , i = 1, 2;
611 (t, r) = diU1 — Zd2W + Ef3’ (Z)diS*3) + 0,5(diw)2, s s22 (t, r) = (R + z) 1 [(R + z) R-1d2u2 + d2 w + w+
+ E f' 3 ) ( z ) d 2 6 3 ] + 0,5 ( R + Z ) -2 ( d 2 w ) 2 , s
2 e 12 ( t , r ) = ( R + z )— 1 [ 5 2 u — z 5 1 5 2 w + E ft3 ) ( z ) 5 2 e (3) ] + s
+ ( R + z ) R ^d u 2 + d1d2 w +
+ E f 2 3 ) ( z ) 5 1 e <2 3 3) + ( R + z )— 1 5 , w 5 2 w ; (2)
s
U 1 ( t , r ) = U 1 ( t , x ) — z 5 1 w + E /((3 ) ( z ) б (3) ( t , x ) , s
U 2 ( t , r ) = ( R + z ) R — 1 u 2 ( t , x ) +
+5 2 w + E / 2 3 ) ( z )6 23) ( t , x ) ; (3)
s
U 3 ( t , r ) = w ( t , x ) , x gQ, |z | < h , t > t 0,
Q = { x : 0 < x 1< L , 0 < x 2< 2 n } ,
./'- ' ( z ) . 2 h - [ h = ф ;- ( z ) — ф ;- -( z ) ] (i = 1,2), ф ( 3 ) ( z ) = h — 3 ( 1 + 3 )— 1 z 3 + 1 , Ф * 3 ) ( z ) = h — 3 ( R + z ) T 3 ( z ) ,
( — 1 ) m R m z 3 - m
( )-- R 3 In ( R + z ) ;
s — 1
^ 3 (z )-E m=0
3 — m
> ^3
p
O
X
h
h
R
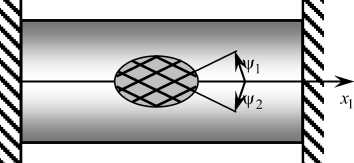
Рис. 1. Цилиндрические КМ-оболочки: а – жестко закрепленная только на левой кромке; б – жестко закрепленная на обеих кромках
Fig. 1. Cylindrical shells clamped only along the left edge ( a ) and clamped on both edges ( b )
е ( k ) - коэффициенты частичных сумм разложений деформаций поперечных сдвигов е.3 по степеням переменной z ; K - целое число, равное количеству слагаемых, удерживаемых в этих разложениях; z - введенная для удобства новая радиальная координата, отсчитываемая от срединной поверхности; w - прогиб точек этой поверхности ( z = 0); ux , u2 - продольное и окружное перемещения точек срединной поверхности; t0 - начальный момент времени t ; r - вектор места точки конструкции; x - вектор места точки срединной поверхности; Q - область, занимаемая этой поверхностью в координатах xx2 ; суммирование по индексу s проводится от 0 до K , как это указано в (1). Равенство (4) - традиционная для тонкостенных элементов конструкций кинематическая гипотеза, согласно которой изменяемостью поперечного перемещения U3 ( t , r ) в радиальном направлении х3 можно пренебречь [5-18, 21-23, 29]. Таким образом, в равенствах (1)-(4) при учете выражений (5) неизвестны функции w , и. и е ( S ) ( i = 1, 2, 0 < s < K ), зависящие от времени t и только двух пространственных переменных хх и х2 . При K = 0 из (1)(5) вытекают кинематические соотношения теории Редди [15-17, 23].
Поскольку исследуется динамическое поведение КМ-оболочки как гибкой тонкостенной механической системы, то напряжение о33 ( t , r ) с приемлемой для практических приложений точностью можно аппроксимировать линейно по поперечной координате z [11]:
О 33 ( t , r ) =
a ( + ) ( t , x ) -a ( 3) ( t , x ) Th z
+ °33) ( t , x W- ) ( t . x )
x gQ, |z | < h , t > t 0,
где a ^l) ( t , x ) . a33 ( t , x , ± h ) - нормальные напряжения на внешней (+) и внутренней (–) лицевых поверхностях, известные из соответствующих силовых граничных условий (так, на рис. 1, а изображен случай, когда a? . 0 и a 33) =- p ).
Двумерные уравнения движения тонкой цилиндрической оболочки, соответствующие аппроксимации перемещений (3) и (4), при учете (5) и (6) имеют вид [23]:
p u (1) =d ( M <Р - M ( l ) q w ) + S2 ( M 3 1 ) - M 3 1 : d w ) - - 1M 3 1 - 1) + lM 3 1 - 1) d w -
-
J
[a
+)
-
(
-
I
)
1
a
3)
]d
,
w
+
Xi1
)
(
t
,
x
)
,
p
u
31)
= d
(
M
-
M
3
1
)
d2
w
)
+ d2
(
M
3
1
)
-
M
3
1
)
d2
w
)
-
-
1M
3
1
1
+
1M
3
1
3
1) d2
w
-
- hl [(R + h)"' a+) -(-1)1 (R - h)"' a-) ] X x d2 w + M* 1) + X31) (t, x), 2hpw = 5, (Mp' + M^d w+M<20)d2w) +
+
62
(
M
230)
+
M
11
d
w
+
M
И
d
w
)
-
(7)
- M20) -a+) -оЗ-) + X230) (t, x), x gQ, t > t0, 0 < I < K +1, где p=p0 ®0+£ pk ®k, ®0=1 -]E ®k, k=1 k=1
X
31)
(
t
,
x
)
=
J
X
(
t
,
r
)
zdz
,
-
h
M
j
)
(
t
,
x
)
^
J
о
j
(
t
,
r
)
zdz
,
3
h
ML"
(
.
,
x
)
.
j
a
j
i
t
ii)
z dz, '' V ’ J, R
+
z
-
h
Й,
")
(
t
,
x
)
.
J
a
j
i
t
iL
1
z dz,
i
j V ’
-
h
(
R
+
z
)
2
um (t, x).JUm(t, r)z dz, - h iM<3-1) (t, x)=1J озз (t, r) z-1 dz = h- [(a3+)+ a33) )x
3
h
2
x (13 (-1)1)+txj (a3+)3 °33) )(1+(-1)1)], Im<1-1) (t, x ) = 1J O33r (t ’r) z31 dz = = ^(o3+) +o3 3) )(X( h )-T1(-h)) + + 1(a3+) -a33) )(X-1 (h)-X-1 (-h)), 0 < 1 < K +1, i, j = 1,3, m = 1, 2;
о
у
- усредненные напряжения в композиции; p0, p^ -объемная плотность материала связующего и арматуры
k
-го семейства;
X
- компоненты объемной нагрузки, действующей на КМ-оболочку; точка - производная по времени
t
. Согласно четвертому равенству (8), в рамках гипотез, используемых для тонкостенных элементов конструкций, некоторым из введенных силовых факторов можно дать механическую трактовку:
M
(0)
.
F
,
M
(у)
.
My
- приближенные выражения для мембранных усилий и изгибающих и крутящих механических моментов;
M
z
(
3
0)
.
F
3 (
i
,
j
=
1, 2) - приближенно представляют собой поперечные силы; остальные силовые факторы
M
(
1
)
,
M1р
и
M^
, определенные в (8), - моменты высших порядков от напряжений, вычисленные с весами
z1
,
(
R
+
z
)
1
z
1
и
(
R
+
z
)
2
z
1
соответственно.
Материал
k
-го компонента композиции предполагается однородным и изотропным, а его определяющие уравнения вязкоупругопластического деформирования при учете (6) можно записать в матричной форме [18]:
a
k
=
Z
k
=
k
+
Vk
„
к
+
w
к
У'.
+
(
B
(
k
)
-
D
(
k
)
)
„
33
] +
q
k
„
33
,
=
(
k
)
=
g
T
4-
e
T
O
+
z
(
k
)
[„33
+ (
B
(
k
)
-
D
(
k
)
)o33] , 0
<
k
<
N
.
33
OK k k k
33 33
Здесь и далее:
Z
k
=
Z
.
-
Z
k
,
V
k
=
V
k
-
V
k
,
к
=
0,1
N
; (10)
a
k
=
{
„^
di\
a
-
\ „м
-
)
)
T,
■И1,
as,
„
1;'
,
„
';'
,
a
-
'
}
T
,
•
,
=
(
=
;
-
-
.
=
^
-
>
,
=
(
",
=4"
,
=
5
k
'
)
T
.
= U
(
k
) P(
k
)
k
)
k
)
k
'IT
~ {=11 , =22 , ^=12 , ^=13 , ^=23 } , s, ={ si), s 2 ", s"^4*\ s5 "}T .
= L(
k
) „(
k
) Д
k
) „(
k
) л
k
)1T.
~
{
s
11
,
s
22
,
s
12
,
s
13
,
s
23
}
;
(k)\ /=(k)\ _/-(k)\ k)\ z- =(zj ), zk =(zu ), Vk =(vj ), Vk =(vj ) - 5х5-матрицы, wk {ni k)}, q = {qik)}, gk ={gk)} , ek = {ek)} - пятикомпонентные вектор-столбцы, ненулевые элементы которых определяются так:
z
(kk
)
=
25^
G
(
k
)
+ A
(
k
)
,
z
(
k
)
=
G
(
k
)
,
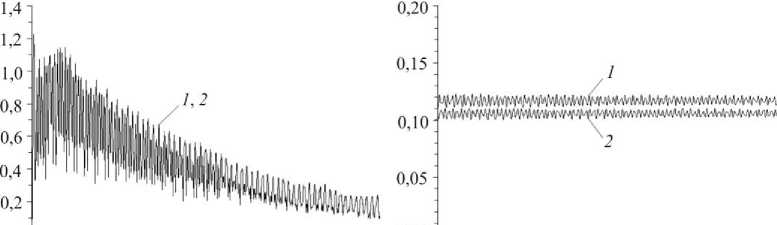
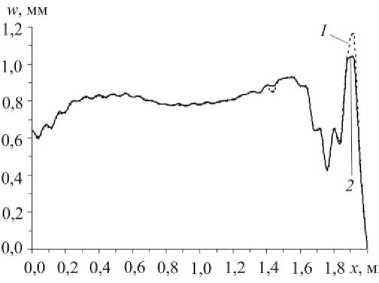
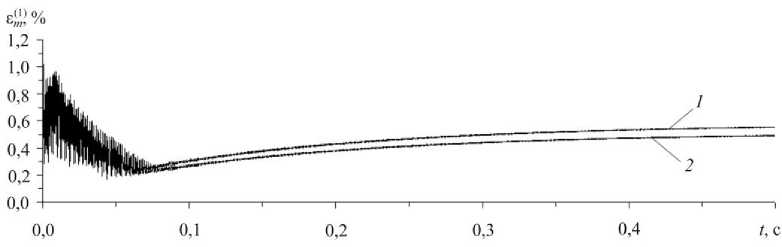
z*k) = A(k)s(k)s = A - s“ - [ s‘ - - z“) s; k) (xui-A") s“' s; k')], l v* k) = -5.B(k) + D(k), v(k) = - B(k), V<k>= D(k>z(k) (a(k) - A<k)s,:k)s(k)), Z(k) - _ n(k) z(k) д(k) e(k) v(k) и/k) - z(k) h (k) _ Д'k) v(k) s' k) 1 vlj — z sZ s33 , ’*! — z I '^ si s33 J, w;(k) =- A(k) z(k) a( k) s(k), q,(k) = D(k), g p(k>(';<k) G)k) ( (kk) (k) = c G----- (k) =G_c---- (1+g(k)) T<k>2, n(k) I 1+g(k) 1 ( К(k) G)k) П (k )=- R( k)- K__ a( k) =G__ D 3 (B ц(k)J, g G(k), E(k) (k)_ v(k)E(k) 2 (1 + v(k)), (1 + v(k))(1 - 2v(k)), ТГ (k) 1 5 K(k) _ E T).k)2 _ £ ( (kk)2 (k)2 (k)2 \ X- (k)2 K = 3(1 -2v“)),T = 2(s' +s2 +s” )+;:r„ , s*) = ak)-6,„4" У, j = 173), r, 1 ]Г„Ц w _ Jo при T(k) < T(k) или T(k) = T(k) и W(k) < T(k)2 / Пk), = [1 при T(k)= T(k)и W(k)> T(k)2/ n(k), W“).>;=, + z")s“){[*„ +(B*'-D"))a„]- -D(k4ty(kk))- X(kЧё(k)+£(k)1 + Л)k)s(ki D („11 +„22 ) A (=11 += 22 ) + A s33 sk = k } , Tjk)= max{Tp), Tmk’}, 0<k<N; (12) „(k), =(k)- компоненты тензора напряжений и деформаций; E^k), v(k)- модуль Юнга и коэффициент Пуассона; n(k)— коэффициент линейной вязкости при сдвиге; ц(k)- коэффициент объемной вязкости; T(k)- значение интенсивности касательных напряжений T(k), при котором впервые достигается пластическое состояние; T^k)- максимальное значение T(k), достигнутое за всю предыдущую историю деформирования элемента материала; 5у - символ Кронекера; индекс T - операция транспонирования; индекс k – номер компонента композиции (k = 0 - связующее, k > 1 - волокна к -го семейства). Соотношения (11) задают соответствия между пятью компонентами f.(k)(i = 1, 5) некоторого вектор-столбца f и компонентами симметричного тензора второго ранга f (kk)(j, l = 1,3, 0 < k< N). Соотношения (9) при учете (10) и (12) получены в предположении, что малые деформации =(k)могут быть разложены на вязкоупругие e<k)и пластические p(k) (несжимаемые) составляющие. При этом мгновенное пластическое деформирование определяется уравнениями теории течения с изотропным упрочнением [27], а вязкоупругое деформирование – уравнениями модели тела Максвелла – Больцмана [18, 28]: А ( k ) Д k ) e(k)= sj + siu_ e(k) ij 2G(k) 2n(k) , й (k) су(k) k)_ „0 =0 3K(k) 3ц(k), (13) i, j = 1,3, 0 < k < N, где 1 3 13 e (k) - AV e(k) g(k) -АУе( k) =0 = a ^ = ll , e0 = 2 ^ ell , 3 l=1 ^k)= ej)-5ieok\ i, j=173. Если вязкие свойства в (13) не учитываются (n(k)^^ и ц(k)^да), то эти соотношения при учете (14) редуцируются в закон Гука, а равенства (9) – в определяющие уравнения ТПРХ [23, 27], так как согласно (10) и (12) имеем B(k)= D(k)= 0 и V(k)= 0. Используя соотношения (9) и повторяя рассуждения из [18], для текущего момента времени t получим следующее определяющее уравнение, записанное в матричной форме и описывающее вязкоупругопластическое деформирование волокнистой композиции рассматриваемой цилиндрической оболочки: d = Ве+р,(15) где В н. Во + £ЮkВk Еk)H-1, k=1 N p - f - Bg, f .„p,, +X®k (Pk + В krk ) , k=1 NN H=^„I+X®kЕk, g-E®krk, k=1 rk - D-^, Ek — D-1Ck, 1 < k< N; d, e - пятикомпонентные вектор-столбцы скоростей усредненных напряжений 6у и деформаций гу в композиции, по структуре аналогичные (11); B, Е^, Ck -5х5-матрицы; D-1, H-1 - матрицы, обратные 5x5-матрицам D и H; p, f, g, r, с — пятикомпонентные векторы-столбцы. Элементы c(k), d(.k) матриц Ck, D и компоненты с(k) вектор-столбцов с определяются по формулам (55) и (56) из [18] и зависят от механического состояния k-го материала композиции и направлений армирования, т.е. от углов ^к (см. рис. 1, б). Для однозначного интегрирования исследуемой начально-краевой задачи необходимо задать начальные и граничные условия. Если на торцевой поверхности КМ-оболочки (x = 0 и/или x = L) заданы силовые граничные условия, то для силовых факторов, введенных в (8), получим [23]: n (м*p - м (1) at w) = p(1) (t, x), n (м- м*;)a2w) = p(1) (t, x) (0 < i < k+1), и (м (0) + м (0) a, w+м^ а2 w) = р(0) (t, x) , х, = 0 ’ (17) и/или x = L, 0 < x2 < 2n, t > t0, где P1) (t, x) - \Pj (t, r) zldz, j = 1,3, x = 0 (18) и/или x = L, 0 < x< 2n, |z| < h; ру - заданные на торцевой поверхности внешние распределенные нагрузки, действующие в направлениях X (j = 1,3); и = 1 при х = L и и = -1 при х = 0 • Если на торцевой поверхности оболочки заданы кинематические граничные условия, то для обобщенных кинематических переменных, введенных в (8), при учете (4) имеем равенства [23]: w(t, x) = U,3 (t, x), ui1) (t, x) = u(1) (t, x), x = 0 и/или x = L, 0 < x2 < 2n, t > t0, (19) i = 1,2, 0 < I < K +1, где u(l)(t, x)-Ju.(tt, r)zldz, i = 1,2, 0< 1<K +1; (20) - h U - заданный на кромке прогиб; U - заданные на торцевой поверхности оболочки тангенциальные перемещения в направлениях x. (i = 1, 2). При t = t0 следует использовать начальные условия (см. (4) и (8)) [23]: w ( t0, x) = U03 ( x), w ( t0, x) = V03 ( x), ui1) ( t0, x) = u0? ( x), (21) U(1) (t0, x) = v(।) ( x), x gQ, i = 1,2, 0 < 1 < K +1, где hh u0 ? ( x )-j U0i( r ) z'dz , v01) ( x )-j V0i( r ) z'dz , z?9x - h - h (22) i = 1,2, 0 < 1< K +1; U^j, V7(j = 1,3) - известные в начальный момент времени t перемещения и скорости точек КМ-оболочки. Кинематические переменные w, u. и e(S) (0 < s< K), использованные в (1)–(4), и обобщенные кинематические переменные u(1) (i = 1, 2 , 0 < 1< K+1), введенные в (8), связаны матричными равенствами [23] Ei. = C-’u,.+ wdw, i = 1,2, где u,={uf’, u,(1), u,<2’,..., uiK), u(K+1) }T, о =su F(0) F(i) F Ei {ui, ei3 , ei3 , ..., ei3 , ei3 } ; C-1- матрицы, обратные (K + 2) x (K+2) -матрицам Cz , wz - (K + 2) -компонентные вектор-столбцы, элементы которых определяются по формулам (31) и (33) в [23] независимо от решения исследуемой задачи. Если в текущий момент времени t из каких-либо соображений известны значения функций w и u(1) (0 < 1< K+1), то из уравнений (23) при учете (24) можно вычислить значения функций uz., e(s) (i = 1, 2 , 0 < s< K), характеризующих усредненные деформации композиции (1), (2) и тангенциальные перемещения (3) точек цилиндрической КМ-оболочки. 2. Метод расчета Как отмечалось выше, для численного интегрирования рассматриваемой задачи используем метод шагов по времени [12, 18, 23, 29-32], т.е. будем определять неизвестные функции в дискретные моменты времени tn^j — tn + t (n — 0,1,2,...), где t — const > 0 - шаг по времени. При этом, согласно [18, 23], предполагаем, что в моменты времени t — t уже известны значения следующих функций: mm w ( x ) = w ( tm , x ), u( l) ( x ) = u( l) ( tm , x ), am± Чх^о*±4t x ) dm± 4x) = d( ±Ht x) °33 (x) —°33 (tm , x) , °33 (x) —°33 (tm , x) , mm °j( r >° A tm , r ) ’ ° k ( r I ° k ( tm , r ) ’ (25) m Xj( r )S Xj( tm , r ), i — 1, 2, j — 1,3, m — n -1, n, 0 < l< K +1, 0 < k< N, x eQ, |z| < h. Используя выражения (8) при учете (25), в данный момент времени t можно вычислить все силовые факторы M), M>и M) , входящие в уравнения (7), и граничные условия (17). Как и в [18, 23], производные по времени t аппроксимируем центральными конечными разностями на трехточечном шаблоне {t1, t, tj }. Это позволяет построить явную численную схему типа «крест». Замена вторых производных по времени в левых частях равенств (7) при учете обозначений, аналогичных (25), приводит к уравнениям Thn (n+1 n n-1^ ( n n n _nn\ -^-l w -2 w+ w I = 5,1 M^ + M^ d w + M‘^ d2 w 1 + t V 7 I7 n =„..n + S2 Mg> + M^ d w + M^ d2 w nnnn - M £) + °3+)-о'-)+ X3(0), _ ( n+1 n n-1 A ( n n _P_| „(1)_?7/i)+,/i) I-я I д/f*i)-A/f(i)я 2 U^ 2 u^ + u^ — d| 1V± 11 1V± jg C^ ^w t2 v1 11 7 11 11 13 1 + d21 Mn(l) - Mn'’ 5; w | - l Mg1' +1M^' 5, w- hl X X nn °+’-(-1)l ° nn 5, w + X*l), _ ( n+1 n n-1 Л ( n n P I 7/(l) ?7/(l1) I-Я I /f(l) Д?(l)Я — l U2- 2 U + U I = d) l M21 - M13 ^2 w I + n n n + d2M nnn - lM X (R + h)-1 о*+ ’-(-1)l (R-h)-1 о*-’ nn n S2w + M<l’ + X<l), 0 < l< K +1, x eQ, n —1,2,3,... На основании (8) и (25) получаем, что правые части в (26) известны. Добавив к этим уравнениям необходимые граничные условия (17) и/или (19) при учете (18) и (20), можем определить по явной схеме значения функ- n+1 n+1 ций w и ui(l) (i — 1, 2 , 0 < l < K+1) в следующий мо мент времени tn^г. Далее по формулам (23) при учете n +1 n+1 (24) вычисляем функции ut и s(3) (i — 1, 2 , 0 < s< K), используя которые по формулам (1) и (2) получаем n +1 усредненные деформации композиции s. в каждой точке конструкции. Последующее решение рассматриваемой задачи при учете соотношений (15) и (16) строится совершенно так же, как и в [18, 23]. Согласно структуре левых частей уравнений (26), для начала расчета по разработанной явной схеме тре-0 0 буется знать не только значения функций w и uz(l) , из вестные из начальных условий (21) при учете (22), но и 1 1 значения функций w , ui(l) (см. (26) при n — 1). Значения этих функций определим по формуле Тейлора при учете начальных условий (21) и уравнений движения (7), рассмотренных в момент времени t —10 [23]: 1 0 w ( x) — w (x) + t w ( x) T2 0 / X + y w(x) +O (T) , 1 0 0 _2 0 (l) u)l) й(l) H)l) 3 ui ( x) — ui ( x) + T ui ( x)+ 2 ui ( x) + O (T ) , i — 1,2, 0 < l < K +1, x eQ. В случае замкнутой круговой цилиндрической КМ -оболочки область Ω (см. (4)) является прямоугольной, поэтому после аппроксимации в равенствах (17) и (26) производных 8. (•) по пространственным перемен ным xt их конечно-разностными аналогами от уже известных (см. (8) и (25)) в данный момент времени t сеточных функций окончательно получим явную численную схему «крест» [12, 18, 23]. Необходимые условия устойчивости схемы «крест» вытекают из критерия Куранта - Фридрихса - Леви и для тонкостенных элементов конструкций приведены в [12]. В случае волокнистой оболочки эти условия выполняются с запасом, если выполняются для каждого компонента композиции в отдельности. 3. Обсуждение результатов расчетов В качестве конкретного примера рассмотрим динамическое вязкоупругопластическое и упругопластическое поведение тонкой длинной цилиндрической оболочки радиусом R — 1 м , длиной L — 4 м и толщиной 2h — 1 см (2h / R —1/100). Конструкция жестко закреплена на обеих кромках: U3 = 0 и u*l) = 0, i — 1, 2 , 0 < l< K+1, x — 0 и x — L (см. (19), (20) и рис. 1, б), и нагружается равномерным внутренним давлением по закону (см. (6)-(8), (25) и (26)) [29]: ^3+) S 0, -Q<-) = p (t ) = _ ^Pmax t / tmax,0< t< tmax, (27) _Pmax exP [-« (t - tmax )] , t > tmax , где (28) , min max , min max; tmax— момент времени, в который p (t) достигает наибольшего значения (p = p^ > 0); t^ - момент времени, при превышении которого можно пренебречь p (t) по сравнению с p^ (согласно (28), p (tmin )= 0,01pm,x ). Примем pmax = 3 МПа , tmax = 0,1 мс и t^n = 2 мс . Эти значения условно соответствуют давлению, вызванному воздушной взрывной волной [29]. Внешние массовые нагрузки не учитываем: X. = 0, i = 1,3 (см. (8)). В начальный момент времени t = t0 = 0 оболочка покоится: UOi = 0 и Vo. = 0, i = 1,3 (см. (21) и (22)). Конструкция изготовлена из эпоксисвязующего и усилена стеклянными волокнами марки S-994. Мгновенное упругопластическое деформирование материалов композиции при активном нагружении определяется билинейной диаграммой растяжения – сжатия ' E(k)8, 18|<8S k) =aSk)/ESk), CT = < sign (8) CT(k) + Esk) (8 - sign ( 8 ) 8(k) ), Is|>8Sk), 0 < k < N, где ст и 8 - осевое напряжение и деформация; Ek) -модуль линейного упрочнения материала k-го компонента композиции; ст(k), 8(k) - условный предел текучести и соответствующая ему деформация того же мате- риала. Физико-механические характеристики компонентов композиции приведены в таблице, в которой принято ц(k) ^^, т.е. объемная вязкость материалов не учитывается (см. (12) и (13)). Физико-механические характеристики компонентов композиции [24, 25] Physical and mechanical characteristics of components of the composition [24, 25] Материал p, кг / м3 ν CTs, МПа E, ГПа Es, ГПа n, МПа • с ц, МПа • с Эпоксисвязующее 1210 0,33 20 2,8 1,114 150 ^ Стекловолокно S-994 2520 0,25 4500 86,8 6,230 600 ад Конструкция армирована в окружном направлении (^=п /2; см. рис. 1, б) с постоянной плотностью ц = 0,3 . Для длинной тонкой цилиндрической оболочки такая структура армирования является рациональной [8, 23, 33]. При указанных условиях закрепления, нагружения и армирования рассматриваемой оболочки она деформируется не только осесимметрично (решения соответствующей начально-краевой задачи не зависит от окружной координаты x ), но и симметрично относительно центрального сечения ^ = L /2 (т.е., например, w(t, x) = w(t, -x), |x| < L /2, x = x -L / 2 и т.п.). На рис. 2 изображены поперечные колебания точек центрального сечения оболочки (w* (t) = w(t, x) , x = 0), полученные по ТПРХ (рис. 2, а, который полностью совпадает с рис. 3, б в [23]) и по теории вязкоупругопластического деформирования материалов композиции конструкции (рис. 2, б). Рис. 2. Осцилляции прогибов точек центрального сечения тонкой длинной цилиндрической КМ-оболочки, рассчитанные по ТПРХ (а) и по вязкоупругопластической теории (б) деформирования компонентов композиции Fig. 2. Oscillations of the deflections of the central section points of a thin long cylindrical CM-shell calculated by the Prandtl-Reuss-Hill theory (a) and by the viscoelastic theory (b) of the deformation of the composition components wm,CM Wm,CM 0,0 -I----1—।----1—।—i—।—।—।----1—।—।—।—।----1—।—i 0,00 —r—।—।—।—।—।----1—।—।—।—।----1—।----1—।----1 0 10 20 30 40 50 60 70 80 90 6 mc 400 410 420 430 440 450 460 470 480 490 Г, mc а б Рис. 3. Осцилляции максимального по модулю значения прогиба вязкоупругопластической КМ-оболочки в окрестности начального момента времени (а) и в окрестности момента времени t = 500 мс (б), рассчитанные по разным теориям изгибного деформирования Fig. 3. Oscillations of the maximum modulus of deflection of the viscoelastic-plastic CM-shell in the vicinity of the initial instant of time (a) and in the vicinity of the instant of time t = 500 mc (b), calculated according to different theories of bending deformation Расчеты проводились по уточненной теории изгиба КМ-оболочек при K = 5 (см. (1)). Согласно поведению зависимости w, (t), приведенной на рис. 2, а, при расчете рассматриваемой конструкции по ТПРХ она неограниченно долго осциллирует, что не позволяет определить величину остаточного прогиба точек центрального сечения оболочки. Поведение же кривой на рис. 2, б свидетельствует о том, что при расчете по вязкоупругопластической модели колебания прогиба точек центрального сечения к моменту времени t = 150 мс практически полностью прекращаются и остаточный прогиб имеет значение порядка 1 мм. На рис. 3 изображены зависимости от времени наибольшего по модулю значения прогиба КМ-оболочки (wm (t )= max |w(t, %! )|), рассчитанные в окрестности начального момента времени (рис. 3, а) и в окрестности момента времени t = 500 мс (рис. 3, б). Кривая 1 получена по теории Редди (K = 0), а кривая 2 - по уточненной теории при K = 5 (расчеты проводились по вязкоупругопластической модели деформирования компонентов композиции). На рис. 3, а кривые 1 и 2 визуально практически неразличимы. Поведение этих кривых на рис. 3, а показывает, что с течением времени поперечные осцилляции конструкции затухают и к моменту времени t = 500 мс почти полностью прекращаются (см. рис. 3, б). Из рис. 3, б видно, что при t ~ 500 мс кривые 1 и 2 заметно различаются, причем остаточный прогиб, определенный по теории Редди (кривая 1), примерно на 10,4 % больше аналогичной величины, рассчитанной по уточненной теории (кривая 2). В связи с этим представляет интерес рассмотрение эпюр остаточных прогибов, рассчитанных по разным теориям деформирования КМ-оболочки. На рис. 4 изображены зависимости w от x (х = % — L /2), определенные при t = 500 мс , когда поперечные колебания конструкции почти полностью уже прекратились. Кривые на рис. 4 рассчитаны при тех же условиях, что и на рис. 3. Поскольку решение исследуемой задачи обладает симметрией относительно центрального сечения оболочки х = 0 (х = L /2), то на рис. 4 приведены только правые участки соответствующих кривых (при х > 0). Сравнение максимальных значений ординат точек на кривых рис. 4, которые достигаются при х ~ 1,9 м (т.е. в зоне краевого эффекта), показывает, что при t = 500 мс значение w , полученное по теории Редди (кривая 1), на 11,7 % больше аналогичной величины, определенной по уточненной теории (кривая 2). Рис. 4. Эпюры прогибов армированной вязкоупругопластической оболочки в момент времени t = 500 мс, рассчитанные по разным теориям изгибного деформирования Fig. 4. Diagrams of deflections of a reinforced viscoelastic-plastic shell at a time instant t = 500 mc calculated according to different theories of bending deformation На рис. 5 изображены рассчитанные при тех же условиях осцилляции максимальных значений интен- сивности деформаций армирующих волокон s(1) (е™ (t) = maxs'1’ (t, Xi, z), z< h , 0 <X1 < L). Xi , Z Рис. 5. Осцилляции максимальных значений интенсивности деформаций арматуры вязкоупругопластической КМ-оболочки, рассчитанные по разным теориям изгибного деформирования Fig. 5. Oscillations of the maximum values of the strain intensity of the reinforcement of a viscoelastic-plastic CM-shell, calculated according to different theories of bending deformation Сравнение кривых на рис. 5 при t = 0,5 c свидетельствует о том, что расчет по теории Редди (кривая 1) примерно на 13 % завышает остаточную величину е® по сравнению с расчетом по уточненной теории (кривая 2). При t > 0,08 c кривые 1 и 2 монотонно возрастают, стремясь к соответствующим горизонтальным асимптотам и практически уже не осциллируя. Такая особенность поведения этих кривых объясняется ползучестью материала волокон, описываемой вязкими свойствами модели тела Максвелла – Больцмана (см. (13) и (14)). Эта ползучесть вызвана тем, что после пластического деформирования компонентов композиции в них возникают различные остаточные НДС, которые с течением времени стремятся выровняться. Заключение Разработанная уточненная математическая модель вязкоупругопластического поведения цилиндрических оболочек, армированных по эквидистантным поверхностям, позволяет более точно, чем в рамках широко используемой неклассической теории Редди, рассчитывать их затухающие колебания при кратковременных интенсивных механических воздействиях и определять остаточные перемещения и остаточное НДС в компонентах композиции после их пластического динамического деформирования. Выполненные расчеты показали, что даже для весьма тонких (с относительной толщиной порядка 1/100) и длинных цилиндрических КМ-оболочек традиционная неклассическая теория Редди, в первом приближении учитывающая искривление поперечной нормали конструкции, не гарантирует получения величины наибольшего остаточного прогиба и интенсивности остаточных деформаций компонентов композиции с точностью до 10 %. Как известно, для относительно толстых и/или корот- ких цилиндрических армированных оболочек (с относительной толщиной порядка 1/10) такое различие решений, полученных по уточненной теории и теории Редди, становится еще больше [23] и для остаточных деформаций может составлять несколько десятков процентов. Таким образом, для проведения адекватных динамических расчетов вязкоупругопластически деформируемых цилиндрических КМ-оболочек следует рекомендовать применение теорий повышенного порядка точности, в частности, предложенных в [23] и использованных настоящем исследовании. Продемонстрировано, что в тонкой длинной КМ-оболочке остаточный прогиб может сложным образом зависеть от продольной координаты. Так, помимо краевых эффектов в окрестности центрального сечения конструкции может возникнуть локальный эффект, протяженность которого сопоставима с протяженностью зон краевых эффектов (см. рис. 4). Такая сложная форма остаточного прогиба является следствием сложных неупругих волновых процессов, протекающих в динамически нагруженной тонкой КМ-конструкции. Высокопрочные армирующие волокна, имеющие большие пределы текучести и большие значения деформаций, им соответствующие, при деформировании запасают в большом количестве упругую энергию, поэтому амплитуды осцилляций прогиба точек цилиндрической КМ-оболочки в окрестности начального момента времени оказываются существенно (даже на порядок) больше максимальных значений величин остаточных прогибов (см. рис. 2, б и рис. 3). Аналогичное поведение наблюдается и для зависимостей от времени максимальных значений интенсивности деформаций компонентов композиции. Работа выполнена в рамках Программы фундаментальных научных исследований государственных академий наук на 2017–2020 годы (проект 23.4.1 – Механика деформирования и разрушения материалов, сред при механических нагрузках, воздействии физических полей и химически активных сред). AcknowledgementБиблиографический список The research was (partly) carried out within the framework of the Program of Fundamental Scientific Research of the state academies of sciences in 2017–2020 (project No. 23.4.1 – Mechanics of deformation and destruction of materials, media, under mechanical loads, the influence of physical fields and chemically active media).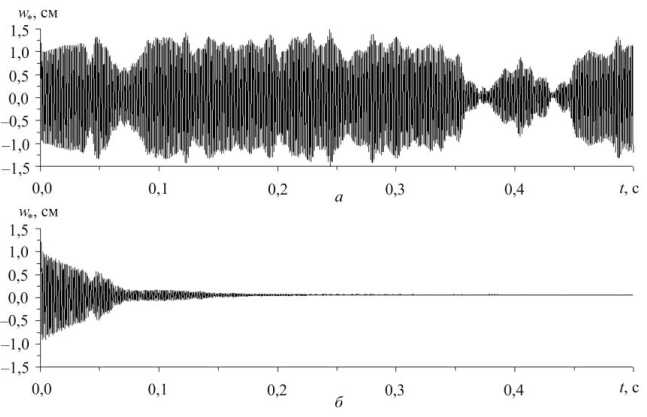
Список литературы Уточненная модель вязкоупругопластического деформирования армированных цилиндрических оболочек
- Bannister M. Challenger for composites into the next mil-lennium – a reinforcement perspective // Composites. – 2001. – Part A 32. – Pp. 901–910.
- Review of advanced composite structures for naval ships and submarines / A.P. Mouritz, E. Gellert, P. Burchill, K. Challis // Compos. Struct. – 2001. – Vol. 53, no. 1. – P. 21–42.
- Gibson R.F. Principles of composite material mechanics. – 3rd ed. – Boca Raton: CRC Press, Taylor & Francis Group, 2012. – 686 p.
- Gill S.K., Gupta M., Satsangi P. Prediction of cutting forc-es in machining of unidirectional glass-fiber-reinforced plastic composites // Frontiers of Mechanical Eng. – 2013. – Vol. 8, no. 2. – P. 187–200.
- Прикладные задачи механики цилиндрических оболочек / Ю.С. Соломонов, В.П. Георгиевский, А.Я. Недбай, В.А. Андрюшин. – М.: Физматлит, 2014. – 408 с.
- Григоренко Я.М. Изотропные и анизотропные слоистые оболочки вращения переменной жесткости. – Киев: Наукова думка, 1973. – 228 с.
- Амбарцумян С.А. Общая теория анизотропных оболочек. – М.: Наука, 1974. – 446 с.
- Васильев В.В., Елпатьевский А.Н. Прочность цилиндрических оболочек из армированных материалов. – М.: Машиностроение, 1972. – 168 с.
- Reissner E. On transverse vibrations of thin shallow elastic shells // Quarterly of Applied Mathematics. – 1955. – Vol. 13, no. 2. – P. 169–176.
- Mindlin R.D., Bleich H.H. Response of an elastic cylin-drical shells to a transverse step shock wave // Trans. ASME. Ser. E. J. Appl. Mech. – 1953. – Vol. 20, no. 2. – P. 189–195.
- Богданович А.Е. Нелинейные задачи динамики цилиндрических композитных оболочек. – Рига: Зинатне, 1987. – 295 с.
- Абросимов Н.А., Баженов В.Г. Нелинейные задачи динамики композитных конструкций. – Н. Новгород: Изд-во ННГУ, 2002. – 400 с.
- Баженов В.А., Кривенко О.П., Соловей Н.А. Нелинейное деформирование и устойчивость упругих оболочек неоднородной структуры: Модели, методы, алгоритмы, мало-изученные и новые задачи. – М.: ЛИБРОКОМ, 2012. – 336 с.
- Шкутин Л.И. Нелинейные деформации и катастрофы тонких тел. – Новосибирск: Изд-во СО РАН, 2014. – 139 с.
- Андреев А.Н., Немировский Ю.В. Многослойные анизотропные оболочки и пластины. Изгиб, устойчивость и колебания. – Новосибирск: Наука, 2001. – 287 с.
- Reddy J.N. Mechanics of laminated composite plates and shells: Theory and analysis. – 2nd ed. – Boca Raton: CRC Press, 2004. – 831 p.
- Андреев А. Упругость и термоупругость слоистых композитных оболочек. Математическая модель и некоторые аспекты численного анализа. – Saarbrucken (Deutschland): Pal-marium Academic Publishing, 2013. – 93 c.
- Янковский А.П. Моделирование вязкоупругопласти-ческого деформирования гибких армированных пластин с учетом слабого сопротивления поперечному сдвигу // Вычис-лительная механика сплошных сред. – 2019. – Т. 12, № 1. – С. 80–97. DOI: 10.7242/1999-6691/2019.12.1.8.
- Whitney J., Sun C. A higher order theory for extensional motion of laminated composites // J. of Sound and Vibration. – 1973. – Vol. 30, no. 1. – P. 85–97.
- Lo K.H., Christensen R.M., Wu E.M. A higher-order theory of plate deformation. Part 2: Laminated plates // Trans. ASME, J. Appl. Mech. – 1977. – Vol. 44. – P. 669–676.
- Куликов Г.М. Термоупругость гибких многослойных анизотропных оболочек // Изв. РАН. МТТ. – 1994. – № 2. – С. 33–42.
- Пикуль В.В. Механика оболочек. – Владивосток: Дальнаука, 2009. – 536 с.
- Янковский А.П. Моделирование динамического по-ведения армированных цилиндрических оболочек при упру-гопластическом деформировании материалов компонентов композиции // Вестник Пермского национального исследова-тельского политехнического университета. Механика. – 2018. – № 2. – С. 133–146.
- Композиционные материалы: справочник / под ред. Д.М. Карпиноса. – Киев: Наук. думка, 1985. – 592 с.
- Справочник по композитным материалам: в 2 кн. Кн. 1 / под ред. Дж. Любина; пер. с англ. А.Б. Геллера, М.М. Гельмонта; под ред. Б.Э. Геллера. – М.: Машинострое-ние, 1988. – 448 с.
- Maćko W., Kowalewski Z.L. Mechanical properties of A359/SiCp metal matrix composites at wide range of strain rates // Appl. Mech. Mater. – 2011. – Vol. 82. – P. 166–171.
- Зубчанинов В.Г. Механика процессов пластических сред. – М.: Физматлит, 2010. – 352 с.
- Фрейденталь А., Гейрингер Х. Математические тео-рии неупругой сплошной среды. – М.: Физматгиз, 1962. – 432 с.
- Houlston R., DesRochers C.G. Nonlinear structural re-sponse of ship panels subjected to air blast loading // Computers & Structures. – 1987. – Vol. 26, no. 1/2. – P. 1–15.
- Zeinkiewicz O.C., Taylor R.L. The finite element meth-od. – Oxford: Butterworth-Heinemann, 2000. – 707 p.
- Librescu L., Oh S.-Y., Hohe J. Linear and non-linear dy-namic response of sandwich panels to blast loading // Composites. – 2004. – Part B 35. – P. 673–683.
- Kazanci Z. Dynamic response of composite sandwich plates subjected to time-dependent pressure pulses // Internation-al Journal of Non-Linear Mechanics. – 2011. – Vol. 46. – P. 807–817.
- Muc A., Muc-Wierzgoń M. An evolution strategy in struc-tural optimization problems for plates and shells // Compos. Struct. – 2012. – Vol. 94, no. 4. – P. 1461–1470.


