Уточненная плоская механико-математическая модель для определения напряжений в основании ленточного фундамента и его упругой осадки

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2020PNRPU MECHANICS BULLETIN

Несущая способность оснований и фундаментов в значительной степени определяется правильной оценкой напряженно-деформированного состояния грунтов и рациональностью выбранных типов оснований [1-6].

Математическое моделирование и оптимальное проектирование современных зданий и сооружений во многом зависят от качества грунта в основании фундамента, которое без перенапряжения должно воспринимать все нагрузки, действующие на конструкцию, обеспечивая ее прочность, жесткость и устойчивость. И в этой связи любые исследования, связанные с модернизацией и совершенствованием методов расчета оснований фундаментов, являются актуальными и перспективными.

Представленная обзорно-тематическая научнопрактическая работа посвящена приложению новых формул фундаментальной двумерной задачи теории упругости [7, 8, 10-13, 17, 21, 27-29] к уточненной количественной оценке напряжений, деформаций и перемещений в основании длинного жесткого фундамента при его одноразовом нагружении [1, 3-6].

Рассмотрим сосредоточенную нагрузку Р , нормальную к границе х = 0 упругодеформируемой полуплоскости х > 0 , материал которой - однородный, сплошной,

изотропный и подчиняется закону Гука, а распределение силового параметра Р по координатной оси z является равномерным (рис. 1).

Существует фундаментальное решение этой задачи, называемое простым радиальным напряженным состоянием

,         2 • P cos 0

° r = ° r ( r ^,0 ) =---- ,

π r

°_в = т = 0, I 0

п I

2 J ,

которое получил в 1892 г. французский ученый А. Фламан [7-10] на основе осесимметричной пространственной математической модели Буссинеска [3, 14, 15]. Формулы (1) удовлетворяют двум уравнениям равновесия без учета объемных сил и условию сплошности среды или уравнению Мориса Леви в полярных координатах r , 0 [7, 8, 10-12, 27-23]:

1 д с„ д т 2 • т „ ---- + — +--= 0, r д 0 д r

r

1. dL + д°т. । °r - °0 =0. r д0 дr       r       ’

d ²     1 д 1

----2 +-----+--2 д r   r д r  r

д2 L

—7 • (°_r + °„) = 0;

д 0 ² J ^{( r 0} ’

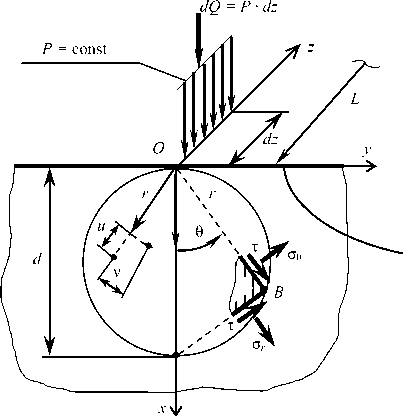
Рис. 1. Расчетная схема напряженного состояния в плоскости xOy

Fig. 1. Design scheme of stress-strain state in the xOy plane

P

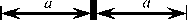
O

K y t—>

( r )

l

--->

где g, g₆, т - нормальные ( o_r, o₆ ) и касательное ( т ) напряжения в произвольной точке В полуплоскости (см. рис. 1).

Граничные условия также соблюдаются, вследствие того что функции о_е и т тождественно равны нулю, а результирующая P • dz внутренних усилий ^_г по принципу Сен-Венана [27–29] заменяется эквивалентной нагрузкой, распределенной по поверхности полуцилиндра малого радиуса ar , т.е.

ππ dz• J Gr ■ a• cosO• d6 = -^ ^ ^z • jcos26• d6 = -P• dz. (5)

"п                           п     0

Оказывается далее, что если провести окружность произвольного диаметра d с центром на оси х, касающуюся верхнего края полуплоскости, где приложена сила Р (см. рис. 1), то для любой точки В этого круга, за исключением нулевой [7, 8, 14], d • cosO = r                     (6)

и на основании (1)

2 • P

G_r =--= const.                 (7)

^r п • d

При этом и наибольшее касательное напряжение τ также остается постоянным [8, 20, 21]: max

° A — ^rP

T max = ^^^ = —7 = const.(8)

2п

Продолжая решение задачи в напряжениях (1), Фламан [9] вывел функциональные соотношения для радиального u = u ( r , 6 ) и кольцевого v = v ( r , 6 ) перемещений точек, расположенных на границе x = 0 по-

π луплоскости при 6 = ± — (см. рис. 1), что, как известно, имеет большое практическое значение для многих технических приложений, связанных прежде всего с физико-математическим моделированием плоских контактных задач [17–20], лежащих в основе расчета подшипников скольжения, цилиндрических катков [15, 17, 26, 32], балок на упругом основании [21, 33] и т.д. Соответствующие формулы применительно к плоской деформации выглядят следующим образом [2, 17]:

u

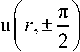
( 1 + ц ) ^ ( 1 - 2ц ) • P

2 • E

v _Г

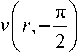
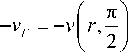
= const,

_ 2 • P . ( 1 - ц ² )

п • E

• ln - ; (10)

где E , μ – модуль упругости и коэффициент Пуассона материала; l – координата произвольно выбранной точки K оси y ( r ) (см. рис. 1), где

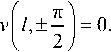
Перемещение v считается положительным, если оно направлено в сторону увеличения угла θ [7]. В дан-

„L п) п) ( ном случае vI r, — | = -vI r,— I (см. рис. 1), и это от-

ражено в равенстве (10).

Можно заметить, что классические зависимости (9), (10) содержат известные и физически не обоснованные противоречия о том, что в случае r = ^ (согласно принципу Сен-Венана [7]) обе функции – (9), (10) – должны равняться нулю, т.е.

^п u_r ад , ± —

Г I      2

п |         |

— = -v ад,— = 0,(12)

2 I      I

однако условия (12) не соблюдаются, так как при r = го

lim и _Б ( r ) = lim v _E ( r ) = 0.             (15)

r ^ro    ^{x 7} r ^to ^{x 7}

и_г = const, | v _r | = ro.

Парадоксальный результат (13) не соответствует и базовому решению Буссинеска (рис. 2) [7, 14, 21], в случае перпендикулярно направленной силы Р на полупространство, в котором отсутствуют вышеуказанные противоречия на граничной плоскости и x = 0 , как следствие,

-Б ( r         P . ( 1 - 2-, )^( . + и ) . 1 = и Б ₍ r ) ,

2 -п- E       r

P-(1-и2 ) 1

vб = v (r ,0) =------7.---= vб (r);

п- Er

откуда, в предельном случае r = ro, получаются нуле- вые ответы:

Для устранения физико-математической некорректности – парадокса (13) – вводим максимально расширенную, по сравнению с (1), модификацию напряженного состояния, возникающего в упругодеформируемой полуплоскости (см. рис. 1):

оr = оr (r,9) * 0, o8 = o8 (r,9) ^ 0, т = т (r,9) ^ 0,

π

0 < r < ro ,0 < 9 < ± —.

,2

Горизонтальная черта над буквенными символами является отличительным признаком принадлежности того или иного параметра к усовершенствованной расчетной модели, изображенной на рис. 1.

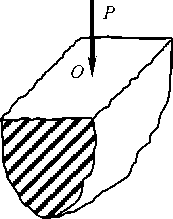
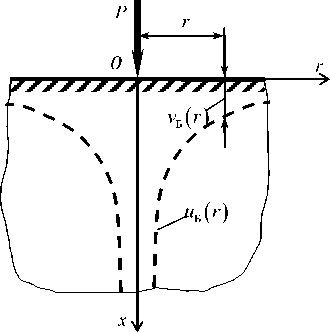
Рис. 2. Пространственная расчетная модель Буссинеска [7, 14, 17] и общий гиперболический характер изменения краевых функций v _E ( r ) , и_ь ( r ) в виде пунктирной кривой линии

Fig. 2. The Boussinesq spatial analysis model [7, 14, 17] and the General hyperbolic nature of the vE (r), uE (r) edge functions’ change - a dashed curve line

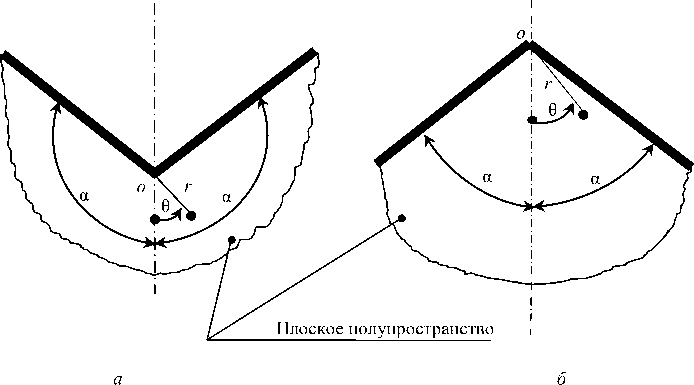
Рис. 3. Схемы углового выреза ( а ) и клиновидной области ( б ), математически аппроксимируемые выражением (17)

Fig. 3. Schemes of angular cut ( a ) and wedge-shaped region ( b ), mathematically approximated by the expression (17)

В процессе определения внутренних силовых характеристик о , d_e , т используем общую фундаментальную формулу [7]

Ф = ф ( r ,9 ) = r^{X + 1} •[ C_T • cos ( X + 1 ) 9 + C ₂ • cos ( X - 1 ) +

+ C • sin ( X + 1 ) 9 + C • sin ( X - 1 ) 9 _] ,          (17)

0 < r < го, 0 < 9 < ± a, функции напряжений ф = ф (r,9), применяемую для расчета элементов конструкций, имеющих форму вырезов и клиньев, включающих угловую точку «О» и плоские боковые поверхности, ограничивающие однородное изотропное полупространство (рис. 3).

Зависимость (17) содержит 6 констант X >  0 (любое число), 0 <а<п,C , C , C ₃, С ₄, которые подбирают, руководствуясь конкретной расчетной схемой, граничными условиями и физико-математическим смыслом рассматриваемой задачи. Доказано также [7], что функция (17) является точным решением однородных дифференциальных уравнений (2)-(4) [7-11, 23, 27] в случае

_   1 дф   1 д2 ф      _   д2 ф о r = о r =---+ —г--7, о9 = о9 = —-, r dr r2  д92             дr2

_   1   д ф   1 д ² ф       д f 1 д ф )

т = т = —-------=------ .

r ²   д 9    r д r • д 9      д r у r д 9 J

Учитывая специфические особенности осесимметричной модели рис. 1, сформулированную уточненную задачу в напряжениях (16) и возможность устранения противоречий (13), принимаем в аппроксимации (17) и на рис. 3, а, б: X = -2 ,а = П = 90°, С = С = 0. В результате, на основании (18) и [7, 22] будем иметь:

О = -2• r"3 •(C • cos9+5• C • cos39),

О = -2 • r3 •(C • cos9+C • cos39), т = 2• r"3 •(C • sin9+3^C2 • sin39),

Первое граничное равенство ов| r, ± П | = 0(22)

θ выполняется, а из второго краевого условия т| r,±П | = 0(23)

I 2J находим

С1 = 3-С2, и тогда, с учетом известных замен [22], cos 39 = 4 • cos39 - 3 • cos9, sin 39 = 3 • sinO - 4 • sin3O,

получаем с точностью до постоянной С 2 функциональные соотношения:

о = о(r,9) = -8• C • r 3 •(б• cos39-3*cos9),

О = о (r, 9) = 8 • C • r-3 • cos39, т = т(r,9) = 24• C2 • r3 •(sin9-sin39).

Для определения коэффициента С 2 , по аналогии с моделью (1)  [7-11], вырезаем из полуплоскости

(см. рис. 1) элемент, ограниченный цилиндрической поверхностью малого радиуса а <^ r. Далее проектируем на ось х внутренние силы, действующие по криволинейной границе полуцилиндра, и внешнюю нагрузку Р :

п

УX = 0, ^2• dz• J(or • cos9-т^sin9)| ^ х х а • d9+P • dz = 0.               (29)

Раскрывая с помощью [22, 25] и (26), (28) интегралы в уравнении равновесия (29) при r = а , вычисляем константу С 2 :

п

16 • С L .         ,         ,         .

—• j( 5 • cos ⁴ 9 - 3 • cos ² 9 + 3 • sin 2 9 - 3 • sin ⁴ 9 ) • d 9 = P , (30) a ₀

16 • С, f 15 • n 3 •п 3 •п 9 • п)   „    „ P • a ²

-+= P, ^ С = a2   ( 16     4     4    16 J          2   6 • n

Исключая С 2 в соответствии с (31) из зависимостей (26)-(28), представляем три компоненты напряжений согласно предпосылке (16):

-   " (         4 • P• а о r =о r (r,9 ) =-------

3 • п

( 5 • cos³9 - 3 • cos9 )

- /        4 • P • а² cos ³ 9

°е ( r,9 )         

3 • п

_             4• P • а ² ( ^{sin9 - sin3}

т = т ( r , 9 ) =--------

π

0 < r <^ ,0 < 9 <± ^П . 2

Подтверждено практическими расчетами и исследованиями, что фактическое перераспределение давления по подошве жесткого фундамента с равнодействующей P незначительно изменяет напряжения в грунте на глубине менее половины размера 2 а [1, 3-6].

Полученные функции (32)–(34), в отличие от известных формул (1) [7–11], включают дополнительный параметр а ², появление которого возможно обосновать [7], так как расчетная схема рис. 1 является идеализированной. В точке приложения линейной сосредоточенной нагрузки Р теоретические напряжения О_г=О_г ( 0,9 ) =

= О = О ( 0,9 ) = т = т ( 0,9 ) = го , поскольку конечная сила Р при r = 0 действует на бесконечно малой площади.

a

° ■“ r _P

a

0,4502

45° 45°

0,4502

б

P

a

0,3796

9,2

0,8488

ст „ • — θP

0,49

a

aa

ст9 ■ — = т ■ — = 0

Ось симметрии

–35,26

a

т ■ —

P

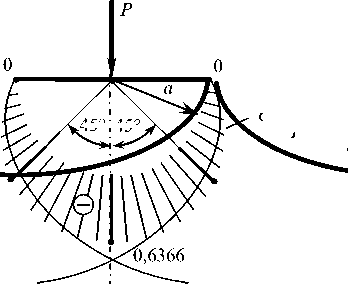
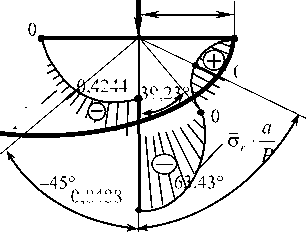
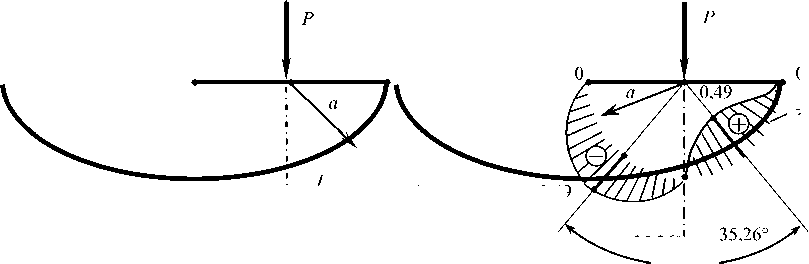
Рис. 4. Безразмерные эпюры напряжений на полуокружности произвольного радиуса r = a : а – по фундаментальной модели (1) [9]; б – в соответствии с выведенными формулами (32)–(34)

Fig. 4. Dimensionless stress diagrams on a semicircle of arbitrary radius r = a : a ) on the fundamental model (1) [9]; b ) according to the derived formulas (32)–(34)

Фактически же нагрузка Р распределяется на площадке хотя и малой, но конечной ширины, в качестве которой будем принимать линейный размер 2 а (см. рис. 1). Численное значение а либо может быть задано, как при исследовании давления жесткого плоского штампа шириной 2 а на упругое тело-полуплоскость [18–20], либо определяется в ходе решения конкретной прикладной задачи, например – контактной о первоначальном взаимодействии по линии z (см. рис. 1) двух параллельных цилиндров, когда параметр а является переменной величиной [17–19], зависящей от Р и физико-геометрических характеристик рассматриваемой механической системы.

Сравнительная оценка решений (1) и (32)–(34) наглядно проиллюстрирована на рис. 4 в количественном и качественном отношениях. Продолжая уточненное решение задачи с использованием формул (6), (32)– (34), легко доказать, что, как и в классическом случае (1) (см. рис. 1), существуют круги Буссинеска [14, 27], или линии равных напряжений (изобары [1, 8]), наличие которых экспериментально подтверждено результатами поляризационно-оптических исследований на лабораторных образцах из прозрачных материалов [28]. В расширенной модели (32)–(34) такими изобарами будут окружности с одинаковыми растягивающими напряжениями (рис. 5)

_    4 ■ P ■ aг

СТ =^--

3 ■ п

cos ³ θ

4 ■ P ■ аа

■

( d ■ cos 0 ) 3     ³ ■ ^п ■ d 3

= const. (35)

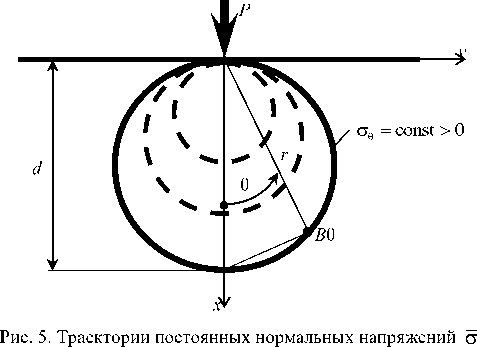
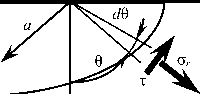
Fig. 5. Trajectories of ст_д constant normal stresses

θ

В инженерной практике при расчете фундаментов необходимо знать распределение напряжений в массиве основания фундамента по горизонтальным и вертикальным сечениям [1–6]. Поэтому переходим с помощью известных аналитических зависимостей [7, 8, 11, 27] (см. рис. 1)

r = 4x 2 + У ², cos0 = x , sinQ = y ;        (36)

rr для одного горизонтального уровня х = а (эпюры ох, ох, т, т^ ) и одного вертикального сечения у = а п = о • cos2 0 + оА - sin2 0 - 2 - т - sin0 - cos 0, xr     θ о = ог - sin2 0 + ое - cos2 0 + 2 - т - sinO - cosO,

^ (37)

т^ = т^ = (о_г - о₉) - sin 0 - cos 0 + т - ( cos ² 0 - sin ² 0 )

(эпюры о , о, ). Наибольшие расчетные значения функций о x ( a , y ) , т yx ( a , y ) , о x ( 2 a , y ) , т yx ( 2 - a , y ) , о ( x , a ) , о ( x ,2 - a ) в виде [8, 29]

от напряжений (32)-(34), т.е. о_г ( r ,0 ) ,о₀ ( r ,0 ) , т ( r ,0 ) , выраженных через полярные координаты r ,θ , к соответствующим внутренним силовым факторам о x ( x, y ) , о y ( x, y ) , т xy ( x, У ) = т yx ( x, y ) в декартовой си стеме отсчета xOy (рис. 6) при допущении [1–6], что грунт представляет собой сплошное линейно-деформи-руемое однородное тело:

o ⁽⁽ max ) ( a ,0 ) =- 0,6366 - P , о⁽_т ^тах ) ( 2 - a ,0 ) =- 0,3183 - P ;

_    _ , x 8 - P - a2x о= о( x, y) =----г,(38)

xx3

^{3 - n}     ( x ² + y ² )

т⁽”^ах >( a , ± 0,577 a ) = +0,207 - P , 4 m ^x >( 2 - a , ± 1,15 a ) = +0,104 - P ;

>

^о у = ^о y ^{( x} , у ) =

4 - P-a^{2 x -} ( ^{x 2 + 3 -} У ² ) 3п ^-   ( x 2 + y 2 ) ³   ,

^т xy =^т yx ^{( x} , У ) = "  4-P- π

a ²

x ⁴ - y

( x ²+ y ² ) 4 ,

о ( ^max ) ( 0,577 - a , a ) = - 0,207 - P , a

о ( max ) ( 1,15 - a ,2 a ) = - 0,104 - P

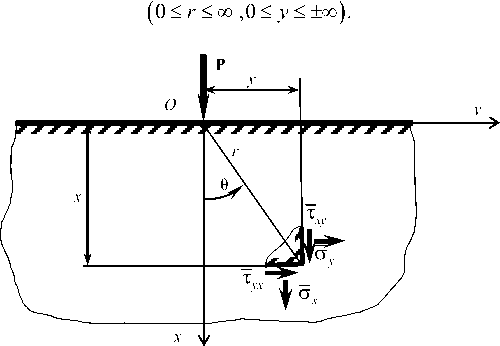
Рис. 6. Схематическая модель к определению напряжений о_х, о _y , т _xy , =т _yx по формулам (38)-(40)

Fig. 6. The schematic model for stress determination о_х , о_у , т xy , =т yx by formulas (38)-(40)

отмечены на рис. 7, б для двух сечений x = a и y = a , а экстремумы зависимостей о_х ( a , у ) , о_х ( 2 - a , у ) , т yx ( a , У ) ,    т yx ( 2 - a , y ) ,   о y ( x , a ) ,   о y ( x ,2 - a ) , как и

( max )                       ( max )

упрощенные      -      ох   (a,0) ,       т^ (a,0) , о^max) (0,577 - a, a) (см. (42)-(44)), удовлетворяющие необходимым условиям [22, 29]

дт    д т      до   д о

^Z x. = ^°l = о, _ x L = _x L = о, =    = о, (45)

д y   д у      д у    д у     д x    д x

записываются следующим образом (см. рис. 7, а ):

о^ )( a ,0 ) = - 0,8488 - P , о ( max ) ( 2 - a ,0 ) =- 0,1061 - P ;

>

т У т” ) ( a , ± a ) = +0,0796 - P , yx                            _a

Vmax ) ( 2 - a , ± 2 - a ) = +0,0099 - P ;

yx                                 _a

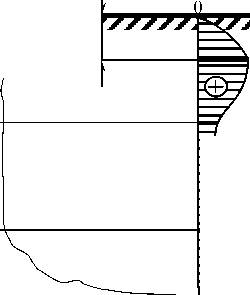
Рис. 7, а , б иллюстрируют соответственно уточненные эпюры о_х, о^ , т и построенные по классическим аналитическим соотношениям [8, 11, 27, 29]

ох = ох (x, У ) = 2 - P — x3 π (x2 + У2)' ■ о У = о У ( x, У ) = 2 - P — xy2 1         (41) π (x 2 + У 2)’ т xy = т yx ( x, У ) = 2 - P — x2y - π (x2 + у2 )2 J оУ”ах) (0,486 - a, a) = -0,54 - P, a _

о (, max ) ( 0,972 - a ,2 - a ) = - 0,0675 - P ;

где место максимума функции о^ (x, y), т.е. координата хо, в общем случае при любой величине переменной y, определяется выражением xo = у - 445-2.

Анализ расчетных данных (42)–(44), (46)–(48) и характера эпюр рис. 7 позволяет отметить некоторые принципиальные особенности новых формул (38)–(40).

Прежде всего, это существенно большие численные абсолютные значения экстремальных нормальных ( max )        ( max )         ( max )        ( max )

напряжений a;  7 > a;  7 , aу 7 > aу 7 и пони женная касательная составляющая |тУmax)| <с | T^mах^| в прямоугольной области 0 < x < a , —a < у < a, близкой к границе (подошве) фундамента. Во-вторых, равенство нулю параметра σ в точках, расположенных на оси симметрии х при у = 0 (см. (41)), по сравнению с

.    4. P • a3

av (x, 0) =-------- ^ 0, 0 < x < ад,

yV 7    3 • п • x3

и различие в знаках напряжений a_y <  0, a >  0. По мнению авторов этой работы, граничное неравенство a >  0 и условие (50) являются более объективными с физико-механической точки зрения (см. рис. 6, 7).

С целью вычисления перемещений u и v верх- ней границы x = 0 материала упругой среды (см. рис. 1) дополняем соотношения (32)–(34):

• дифференциальными    уравнениями    Коши

[7, 8, 10, 11]

8, = 8 r ( r , 9 ) = dL,

- * а - эпюра q

*

б – эпюра σ

—*

а - эпюра т xy

*

б – эпюра τ yx

a

a

Р

O

x

—*

а - эпюра a

P

*

б – эпюра σ

0,486 a

0,54

0,2122

0,0238

О

0,577 a

0,207

a

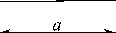
a

x

0,1592

0,0509

a

Ось симметрии

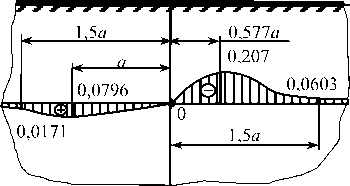
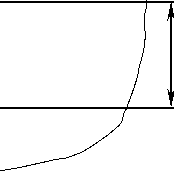
Рис. 7. Эпюры безразмерных напряжений a*, a*, т*у, T*yx, a* , a* в виде соответствующих размерных характеристик, умноженных на  a • P—1: а - по уточненной физико-математической модификации (38)-(40); б - в соответствии с формулами (41), базирующимися на фундаментальном решении Фламана (1)

Fig. 7. a*, a*, т*,, T* , a* , a* dimensionless stress epures in the form of the corresponding dimensional characteristics multiplied x     x     xy     yx     y      y by a • P—1: a - on the refined physical and mathematical modification (38)-(40); b - according to the formulas (41) based on Flamant fundamental solution (1)

-   - /       1 dv  и e6 =e6(r,6)             ■ r 56 r

_           5 v  v 1 5 u

Y = Y( r,6 ) = ----+ - —, dr  r r d6

связывающими относительные деформации с функциями u = u ( r , 6 ) , V = V ( r , 6 ) ;

^e r ,

(52)	X                   r 2
(53)	v = v ( r , 6 ) =
e , у	[ 3 • ц • sin6 + ( 1 — 4 • ц )

2 • P • a ² • ( ! + ц )

3 • п • E r2

• (1 — ц) • cos6 — (5 — 4 • ц) • cos ³ 6 1

⁽      )          ⁽----------------- ^] + Z ( 6 ) ,

• sin ³ 6 1

------^] — fz ( 6 ) • d 6 + ^ ( r ) ;

• зависимостями закона Гука для плоской деформации

где из очевидных кинематических условий задачи

^e _z =e _г ( r , 6 ) = 0

u ( ro , 6 ) = 0, v ( r , 0 ) = 0

в классической интерпретации [8-12]:

° _г = ° _г ( г , ⁶ ) = р( ° r +О б ) =

4 • P • a^г

ц- ( 3 • cos 6 - 4 • cos³

3 • п

r ³

,

следует принять при r = от и 6 = 0 (см. рис. 1)

С ( еМ ( r ) = 0.

1 ^e r ="

—

μ ²

•

E

μ r — 1--°6

^{1 —} ц

4 • P • a ² - ( 1 + ц ) [ 3 -( 1 — ц ) • cos6 — ( 5 — 4 • ц ) • cos³6 ]

Выражения (61), (62) с учетом (64) подставляем в третье физико-геометрическое равенство правых частей соотношений (53) и (58), которое соблюдается тождественно.

Наличие аргумента r ² в знаменателе гиперболических зависимостей (61), (62) гарантирует выполнение необходимых пределов

3 • п • E

r ³

, (56)

lim u ( r , 6 ) = lim v ( r ,6 ) = 0 r ^ro             r ^ro

^{1 ц} 2 ^{e 6}     E

•

μ

6 ^— 1-- ° r

^{1 —} ц

4 • P • a ² * ( 1 + ц ) [ ( 1 + 4 • ц ) • cos 3 6 — 3 • ц • cos6 ]

3 • п • E

r ³

, (57)

Y =——

E

• т =

8 • P • a ² • ( I + ц ) ( sin6 — sin³6 )

п • E

r ³

;  (58)

где ° - нормальное напряжение по направлению оси z (см. рис. 1).

Путем совместного рассмотрения формул (51), (52), (56), (57) получаем систему неоднородных дифферен-

циальных уравнений относительно перемещений V [7, 17, 23]:

u и

при нулевых значениях (64) произвольных переменных интегрирования Z ( 6 ) , ^ ( r ) для всех точек упругоде-формируемого материала рис. 1, аналогичных трехмерной модели Буссинеска (14), (15) [7, 14, 15] (см. рис. 2). В итоге полностью исключаются вышеуказанные противоречия (13) двумерного процесса Фламана [7-12], касающиеся полученных (61), (62) функциональных параметров u = u ( r ,6 ) , v = v ( r , 6 ) в ходе решения данной плоской задачи.

Воспользовавшись соотношениями (36) между переменными r ,6 и x, у , выражаем деформационные характеристики (61), (62), учитывая (64), через декарто-вые аргументы x , у (см. рис. 1):

X

d u _ ⁴ • ^P • a ² ■ ( ! ⁺ ц ) d r        3 • п • E

_          .     2 • P • a ² ^ ( 1 + ц )

u = u (x, у) =--------- X v 7          3 • п • E

[ 3 • ( 1 — ц ) • cos6 — ( 5 — 4 • ц ) • cos ³ 6 j

x •

X —

[ ³ • ( ¹ ц ) • У 2 ^— ( ^{2 —} ц ) • x ² ]

r ³

,

( х ² + У 2 ) ²

,

X

5 v  _   4 • P • a ^ ( 1 + ц )

--+ u =-------------- X 5 6           3 • п • E

[ ( 1 + 4 • ц ) • cos ³ 6 — 3 • ц • cos6 J

r ²

,

откуда, после интегрирования [22, 25],

_  _          2• P • a ² •П + ц )

u = u ( r ,6 ) =--------- x

^{V 7}          3 • п • E

_  _         2• P • a ² ^ ( 1 + ц )

v = v ( x , у ) =---------------- x

⁽     )         3 • п • E

X

У ^[ 3 • ц • x ^{2 +} у ² ( ^{1 —} ц ) ]

( х ² + У ² ) ²

.

Полагая в (66), (67) x = 0 , находим горизонтальное u_r и вертикальное v_r перемещения границы полуплоскости:

u_r = u ( 0, у ) = 0,                 (68)

_             x 2 ' P ' a ² '( 1 — H² ) Г 1 )

V r = V r ( 0, у ) =-----—^------I —I .     (69)

3 ■ n ■ E      у у )

Правомерность расчета u _r = 0 (см. (68)) можно обосновать тем, что в инженерно-технических задачах, например контактных [1–3, 18, 19, 27, 28], на действие поперечной эквивалентной силы P ± у при малых смещениях решающее влияние оказывает функциональный параметр V _r = V _r ( у ) , а компонента u _r<с V_r не принимается во внимание.

В связи с неопределенностью (произвольностью) координаты r = | у | = l^a закрепленной точки K (см. рис. 1) невозможно количественно сопоставить неправильное решение (10) [2, 7, 9, 17] и новый результат (69), однако в качественном отношении такую сравнительную оценку сделать вполне реально, и это показано на рис. 8, графики которого построены по безразмерным формулам

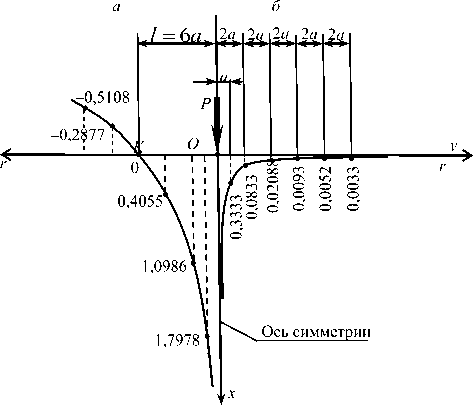
Рис. 8. Общий характер изменения функциональных зависимостей (10) и (69) в безразмерных интерпретациях (70) и (71): а - из решения Фламана [9, 10-12] при l = 6 a ;

б – по выведенной формуле (71) на основе (69)

* ^v Г^*

= ^V Г (I у |)'

п ■ E

2 ■ P - ( 1 - н ² )

-  6 ■ a

= ln-гт

*

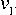
= ^V Г ⁽ У ) '

п ■ E

2 ■ P - ( 1 - H ² )

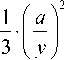
Fig. 8. General nature of changes in functional dependencies (10) and (69) in dimensionless interpretations (70) and (71): a – from

Flaman solution [9, 10-12] at l = 6 a ; b - according to the derived formula (71) based on (69)

адекватным выражениям (10), (69), и по численным данным табл. 1.

Таблица 1

Значения функций (70) (71) при r = | у | >  0, l = 6a

Table 1

Functions value (70) (71) at r = | у | >  0, l = 6a

r =1 у	0	a	2 a	4 a	6 a	8 a	10 a	∞
* v Г	∞	1,7918	1,0986	0,4055	0	–0,2877	–0,5108	–∞
* v Г *	∞	0,3333	0,0833	0,0208	0,0093	0,0052	0,0033	0

Из сравнения выражений (10) и (69) также следует, во-первых, полная определенность в знаке гиперболической функции V _r ( у ) >  0, в отличие от логарифмической зависимости (10), вследствие четности V _r ( у ) по переменной у² при направлении смещения V _r >  0 в сторону увеличения координаты х , а во-вторых – тот очевидный факт, что некорректная формула (10) аппроксимирует только относительную величину v _r (| у |) на замкнутом интервале —1 < у <  l , в отличие от уточненной квадратичной гиперболы (69), позволяющей определять абсолютную осадку границы % = 0 полуплоскости без привязки к точке K (см. рис. 1, 8) в неограниченном теоретически диапазоне —то <  у < то.

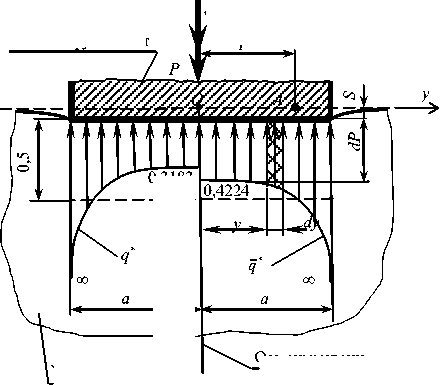
Далее переходим к определению реактивного давления q = q (у) и соответствующей ему упругой осадки S ленточного фундамента [1, 3–6] с шириной подошвы 2a (жесткого штампа) из решения классической контактной задачи [7, 10–12, 19, 20], основу которой, в соответствии с формулой (69), представляет новое неоднородное интегральное уравнение Фредгольма первого рода [10, 11, 30, 31] (рис. 9)

² ■ a ² ■ ( ^{1 —} н ² ) a q(y )■ dy

--^V)    = f ( t ) = S = const, (72)

3 ■ п ■E     —a (t — у )2    JV)V где q = q (у) - искомая силовая функция в виде реакции полуплоскости на участке

—a < у < a, приводимая к известной равнодействующей Р, согласно условию равновесия [10, 11, 17–19]

a

Jq (у )■ dy = P(74)

—a при допущении, что сила Р проходит через середину фундамента (см. рис. 9); t – вспомогательная переменная, изменяющаяся в пределах —a < t < a и представляющая собой координату произвольной точки А, вертикальное перемещение которой от элементарной нагрузки dP = q (у )■ ау                (75)

составляет (см. (69) и (72))

2■ a2 ■(!—ц2) q (у)■ dy d vT =-------- ■ ——--

3 ■ п ■ E

C

a

j ^

—

y ²

V а ² — у²

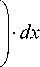
с учетом обоснованного практикой допущения [1, 4, 5] об отсутствии касательных напряжений τ (сил трения) на жесткой прямолинейной границе x + 5 , когда заданная функциональная зависимость f ( t ) [30] равна осадке 5 = const фундамента (рис. 9 и формула (72)).

Q = p_- р ■ а Заданная нагрузка

Жесткий фундамент

0,3183

Ось симметрии

Упругое основание

Рис. 9. Расчетно-графическая модель контактной задачи

Fig. 9. Computational and graphical model of the contact problem

т.е.

' а ² — у^г

a ²        y           y

--arcsin — + а ■ arcsin —

a

a

a

— а

3 -л- а²

C =

2 ■ P

3 ■л■ а²

Подставляя q ( у ) в соответствии с (77), (79) в исходное уравнение (72), получаем, раскрывая необходимые для этой процедуры интегралы [22, 25]:

q ( у ) =

2 ■ P

3 "Л" а а

—

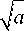
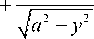
— а <  у <  а ; (80)

4-(1—ц2)■р J 9■П ■ E j

y ²

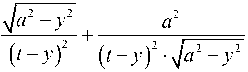
■ йу =

В отличие от абстрактно-идеализированного оригинала (69), в котором направления силы P и перемещения v _r > 0 совпадают (см. рис. 8), в формулах (72), (76) знак «минус» указывает на противоположность действия контактного давления q ( у ) - вверх и кинетической характеристики v _r > 0 - вниз (см. рис. 9).

Уравнение (72) решаем обратным методом [27, 30, 31], руководствуясь экспериментальными данными [1, 5, 6], показывающими, что реактивная нагрузка q ( у ) распределяется неравномерно по подошве жесткого фундамента (штампа), увеличиваясь теоретически до бесконечности по краям у = ± а и понижаясь к центру поверхности контакта (см. рис. 9). Основываясь на опытных результатах [1, 3–6] и после многократных проверок различных функций, аппроксимируем контактное давление q ( у ) следующей аналитической зависимостью:

Замена переменной у :

t — у = w, ^

у = t — w, йу = — dw

4■(l— ц2)■P

--------5-------X

9 ■п ² ■ E

X In

q =

q (У ) = C ■ Vа 2 — у2

2 a ²

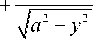
где С – постоянный коэффициент.

Вычисляем константу С из равенства (74) с использованием справочных таблиц [25]:

X j

V

V— w ² + 2 ■ t ■ w + а ² — t¹ w ²

+ а2 ■ j

dw

w

—w2 + 2 ■ t ■ w + а2

4■(l— ц2)■P

= -------9--- X

9 ■ п ² ■ E

dw +

—

t ²

( 2 ■ а ² — t ² ) ■ V — w ² + 2 ■ t ■ w + а ² — t ² w ■ ( а ² — t ² )

+ t l_ ( а ² — t ² ) ■ V O ⁷— ? ⁷

2 ■ t ■ w + 2 ■ ( а ² — t ²) + 2 ■ V а ² — t² ■ V— w ² + 2 ■ t ■ w + а ² — t²

w

—2 ■ w + 2 ■ t

+ arcsin                — =

J4 ■ t ² + 4 ■ ( а ² — t ² )

4^(1— Ц2)■р Г .    —2■ t + 2■ у + 2■ t

—-—— --arcsin—=      =

9^п ■E L       V4■ t2 + 4■ а2 — 4■ t2

( 2 • a ² - t ² ) • 7 - t ² + 2 • t • y - y ² + 2 • t ² - 2 • t • y + a ² - t²

( t ^{- y} ) • ( a ^{2 -} t 2 )

t ³

+--,         x

( a ² - 1 ²) • xa 1

полученным на основе логарифмической зависимости (10), базирующейся на упрощенной модели Флама-на [7–11] простого радиального напряженного состояния (1) (см. рис. 1). Итоги этого сравнения приведены в табл. 2 и на эпюрах рис. 9 в безразмерной модификации

x In

X In

2 • 1 ² - 2 • 1 • y + 2 • a ² - 2 • 1 ² + 2 • V a ² - 1 ² • 4 a ² - y y t - y

t ³

( a ² - 1 ² ) • x!T7

3 • n

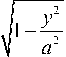
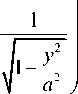
2 • 1 ² - 2 • 1 • y + 2 • a ² - 2 • 1 ² + 2 • 4a ² -

1 ² •

y ²

*

a

t - y

q = q • P⁼ —г Пч /1

—

y ² a ²

- a <  y <  a .

4 • ( l -ц ² ) • P

9 •n ² • E

•

^y arcsin

( 2 • a ² - 1 ²) • ДО" - ?

( ^{t - y} ) • ( a ^{2 - 1 2} )

t ³

⁺ ( a ² - 1 ²) • Ди² - !

Таблица 2

Численная информация к построению эпюр реактивных давлений

x ln

- 2 • 1 • y + 2 • a ² + 2 • V a ² - 1 ² • 4a ² - y² t - y

Numerical information to plot the reactive pressure epure

4 • ( l -ц ² ) • P

—-----X

9 • n ² • E

1 ³             ,   ( - 1 + a ) • a • ( 1 + a )

+-- - • In -----------------------

( a ² - 1 ² ) • V a ² - 1 ²        ( ^{1 -} a ) • a • ( ^{1 +} a )

4 • ( l -ц ² ) • P =    9 •n ² • E

•

откуда будем иметь

S =

n +--

( a ²

t ³

—

t ² ) • ДД

—

= • ln| - 1| ,  (81)

t ²

4 • ( l -Ц ² ) • P

9 •n ² • E

= const,

что подтверждает правильность подобранной функциональной зависимости (80), являющейся точным решением интегрального уравнения (72), когда P = const (см. рис. 1), а ширина подошвы фундамента 2 а и ее проектная длина L находятся в соотношении L ( 2 a ) 1 >  10 [1, 4–6], обеспечивающем адекватность и механикоматематическую корректность использованной здесь расчетной схемы плоского деформированного состояния (32)–(34), (38)–(40), (54)–(58).

Представляет практический интерес оценка предложенной уточненной аппроксимирующей формулы (80) с точки зрения ее сопоставимости с классическим результатом С.А. Чаплыгина и М. Садовского [7, 8, 11]

P q=q(y)=—/2   2, - a - y" a,      (83)

n 4a - y

Table 2

y	0	±0,2 a	±0,4 a	±0,6 a	±0,8 a	±0,9a	±a
—* q	0,4244	0,4245	0,426	0,435	0,481	0,5793	∞
q *	0,3183	0,3249	0,3473	0,3979	0,5305	0,7302	∞

Приводим также характерные величины реактивных распределенных сил, согласно выражениям (84), (85) (см. рис. 9):

– минимальные давления в центре « О » площадки контакта при y = 0

_        PP qmin = 0,4224 • -, q_ = 0,3183 • -;

aa

– средние значения

P q ср = q ср =0,5 • -.

a

В обоих случаях (84) и (85) мы имеем для угловых точек у = ±a (см. табл. 2 и рис. 9)

q ( ± a ) = q ( ± a ) = да.                (88)

Совершенно очевидна зависимость осадки S от линейного размера 2 а . Для учета этого параметра в соотношении (82) отметим прежде всего тот факт, что в условиях плоской деформации (54)–(58) теоретическая длина линейно-полосовой сосредоточенной силы P равна бесконечности по направлению координаты z <да (см. рис. 1). Вследствие этой особенности вводим в решение поставленной контактной задачи общую известную рабочую нагрузку Q на фундамент, распределяя ее равномерно по реальной длине L = в • a его подошвы (см. рис. 1 и 9):

L

dQ = P■ dz,Q = P-Jdz = P■ L, оP =

Q Q

L в ■ a ’

где в — 20 - параметр, учитывающий необходимую для реализации плоской деформации фактическую разницу между продольным L и поперечным 2 а размерами контактной поверхности [1, 3–6], о чем уже было отмечено ранее в пояснении к зависимости (82); с другой стороны, произведение Q ■ в ^{- 1} можно считать частью нагрузки Q , действующей на элемент штампа с площадью основания 2 a х а.

С учетом (89) формула (82) приобретает необходимый окончательный вид

S = S ( а ) =

4 ■ Q-(1 -ц2)

9 ■ п ■ E ■ в ■ а ’

и при этом в случае а ^ 0 абсолютная деформация грунта S ^го при фиксированной нагрузке Q . В этой же связи с увеличением а , т.е. ширины граничной плоскости x = 0 (см. рис. 1), осадка S будет уменьшаться, что реально и конструктивно обосновано.

За пределами фундамента (см. рис. 9) на интервале — а >  у >  а , по аналогии с базовой квадратичной функцией (69), его вертикальное перемещение S y может быть аппроксимировано гиперболической зависимостью

S y = S y ( у ) = S ■    .                (91)

Естественно, что когда у = ± а ,

Sy = S =

4 ■ Q ■(I—ц2)

9 ■ п ■ E ■ в ■ а ’ а если у ^±го, то S (±го) ^0 ; например, уже на расстоянии у = ±5а и у = ±10а будем иметь соответственно: Sy (±5а) = 0,04 ■ S и Sy (±10а) = 0,01 S.

Комплексный анализ проведенных исследований позволяет сделать следующие выводы:

• 1.    Представленное в данной фундаментально-прикладной работе усовершенствованное инновационное решение известной многофункциональной классической задачи Фламана [7–13, 27–29] является принципиально новым и уточненным по существу, так как учитывает три напряжения □ ,., а_д, т , в сравнении с одной компонентой σ в [7–11], а также дополнительный параметр 2 а , характеризующий ширину малой площадки распределения ло-

• кальной нагрузки Р, действующей по направлению нормали к границе полуплоскости (см. рис. 1).

• 2.    Доказано существование цилиндрических поверхностей, где растягивающие тангенциальные напряжения □;, = const >  0 (35) остаются постоянными на круговых образующих – изобарах (см. рис. 5). Аналогичные окружности Буссинеска [8, 11, 14, 27, 29] в виде сжимающих радиальных напряжений a_r = const <  0 (7) выявлены и подтверждены экспериментально-теоретически (см. рис. 1) в упрощенной модели Фламана [28].

• 3.    На основе классической модификации плоской линейно-упругой деформации (54)–(58) выведены формулы функций перемещений (61), (62), (66)–(69), не имеющие противоречий – парадокса (13) [7, 11, 12, 17], вследствие равенства нулю, когда радиальная переменная r стремится к бесконечности, что свидетельствует о их корректности и адекватности с физико-механической точки зрения (см. рис. 8).

• 4.    Получено точное решение (80), (90), (91) фундаментально-прикладной контактной задачи теории упругости о взаимодействии бесконечно длинного жесткого штампа с прямолинейной границей x = 0 деформируемого однородного полупространства (см. рис. 9), материал которого подчиняется обобщенному закону Гука (55)–(58). В отличие от существующего типового решения (1), (9), (10), предложенная механико-математическая модель (32)–(44) позволяет определять не только реакцию основания (80), но и абсолютные вертикальные перемещения (90), (91) (а не идеализированное относительное (10) [17–20] с привязкой к произвольно расположенной точке K (см. рис. 1)) поверхности контакта в неограниченном диапазоне изменения переменной —го <  у < го (см. рис. 9). С помощью существующих методик и алгоритмов [7, 8, 17–20] можно вычислить только контактные усилия, но не граничные перемещения края полуплоскости [19], где x = 0 (см. рис. 1 и 9).

• 5.    Результаты разработанной физико-математической модели, доведенные до расчетных аналитических зависимостей (38)–(40), (90), (91) в декартовых координатах х , y (рис. 6) и проиллюстрированные соответствующими характерными эпюрами (см. рис. 7 и 9), возможно непосредственно использовать для уточненной оценки напряженно-деформированного состояния оснований жестких длинных (ленточных) фундаментов и их упругой осадки [1–6], а также при решении специальных задач [12, 13, 18–20], возникающих в процессе проектирования разнообразных контактирующих деталей и конструкций, применяемых в современном машиностроении [2, 15, 26, 32] и строительстве [1–6, 33].