Уточненный метод расчета устойчивости оболочек вращения в осесимметричном случае

Рассматриваются задачи устойчивости сферической и торообразной оболочек в осесимметричном случае. Для решения используется вариационный подход. Упругая энергия оболочки вычисляется по формуле, приведенной А.В. Погореловым в [1]. Работа сил внешнего нормального давления определяется по точной термодинамической формуле в соответствии с теоремой Эйлера–Бернулли. Вариационный подход с использованием работы внешних сил применялся авторами этой статьи для решения задач устойчивости упругих колец с односторонним подкреплением в работах [2, 3], где приводятся аналитические решения некоторых новых вариационных задач.

Постановка задачи

Предположим, что оболочка вращения, срединную поверхность которой обозначим через S , в результате деформации приобрела форму S . Обозначим через g ij , h ij , g j , hij , i,j = 1 , 2 коэффициенты первой и второй квадратичных форм недеформи-рованной и деформированной поверхности соответственно.

Предполагается, что деформация является осесимметричной. Согласно работе [4], энергию деформации, связанную с переходом из состояния S в состояние S , можно вычислить по формуле:

U s

jj Ф 1 ( е 1 , е 2 , к 1 , к 2 ) ds,

где

Ф 1 =

Eh ³     2    2

24(1 _ _v 2 ) ^{( К} 1 ^{+ к} 2 ^{+ 2 VK} 1 ^к 2 ^{) +}

Для поверхности вращения первая и вторая квадратичная формы поверхности записываются в виде (7) . Для недеформированной поверхности:

Eh _{2   2}

⁺ 2(1 _ _V 2 ) ^{( £} 1 ^{+ £} 2 ^{+ 2 V£} 1 ^£ 2 ) ’

E – модуль Юнга, ν – коэффициент Пуассона, ε 1 – экстремальные значения отношения

Y 2 j =1 ( g j   g ij ) du i du j

Y i, j =1 g ij du i du j

κ 1 и κ 2 – экстремальные значения отношения

и ε 2

{ 1 0 = a ² d9 ² + ( R + a cos 9 ) ² dA ² , [ II о = ad9 ² + cos 9 ( R + a cos 9 ) dA ² .

Используя формулы (3) , (4) , (7) , (8) , (10) , можно получить выражения для деформаций ε 1 , ε 2 и кривизн κ 1 , κ 2 . Квадратичные формы I и II в случае осесимметричной деформации имеют диагональный вид. Поэтому

Y 2 j = 1 ( h ij _ h ij ) du i du j E ij =1 g ij du i du j

Пусть S – является поверхностью, образованной вращением некоторой кривой γ вокруг оси Z :

X = ф ( 9 ) ’ z = E ( 9 ) .                   (5)

Здесь θ – полярный угол в плоскости меридиана. Тогда уравнения поверхности вращения будут иметь вид [4]

ф ‘ ² + г' ² _ a²

£ 1                о ’ a2

ф — ( R + a cos 9 )

^{£ 2}        ( R + a cos 9 ) ² ’

«    = ф ф _ фф _ 1                 (11)

^К 1    a ² V ф ' ² + ^{ф 2} a’

E ф _ cos 9 ( R + a cos 9 ) V ф ' ² + E ' ²

. ^{К 2} = cos ² 9 ( R + a cos 9 ) ² V ф ' ² + E ^{2 .}

Для внешнего нормального давления в соответствии с теоремой Эйлера – Бернулли работа внешних сил равна

A = P Д V,                (12)

x = ф ( 9 ) cos A, y = ф ( 9 )sin A, z = E ( 9 ) ,

где λ обозначен угол в плоскости параллельного круга и 0 6 9 6 9 1 , 0 6 A 6 2 п. Предполагается, что деформация оболочки является осесимметричной. В общем случае первая и вторая квадратичная формы поверхности вращения будут иметь вид [4]

где Д V - изменение объема оболочки в результате деформации.

Как известно [5], объем тела, поверхность которого задается уравнениями x = x(9, A), y = y(9,A), z = z(9,A), определяется (с точностью до знака)

I = ( ф ' ² + /2^ d9 ² + ф ² dA ² ,

II = / E ^ф-фф ' A d9 ² ₊ ^{ф ф}   dA ²

φ ^{′ 2} + ψ ^{′ 2}               φ ^{′ 2} + ψ ^{′ 2}

V =

1   2 П п 2 П п

3 Уо Уо

det

x y x θ   yθ xλ  yλ

z

z _θ    dθdλ.

Устойчивость торообразной оболочки при одностороннем подкреплении

Рассмотрим задачу устойчивости тора, нагруженного внешним нормальным давлением.

Обозначим через w ( 9 ) и u ( 9 ) нормальное и касательное перемещения точек поверхности тора. Декартовы координаты до деформации будут определяться уравнениями

В случае осесимметричной деформации определитель в (13) не зависит от A .

Используя формулы (6) , (8) , (9) , (12) , объем оболочки после деформации можно вычислить по формуле:

2 п 2 П п               ‘ х

V = — J   Ф2 ^ w,u,w ,u‘J d9,

где

Ф 2 = det || a ij || ,i’j e 1:3 ,

x = (R + a cos 9) cos A, y = (R + a cos 9) sin A, 0 6 9 6 2п, 0 6 A 6 2п.   (8)

z = a sin 9,

т.е. для недеформированного тора ф = R + a cos 9 , E = a sin 9 .

После деформации уравнения поверхности будут иметь вид (6) , где

{ ф ( 9 ) = R + ( a + w ( 9 )) cos 9 — u ( 9 ) sin 9, [ E ( 9 ) = ( a + w ( 9 ))sin 9 — u ( 9 ) cos9.

Будем исследовать потерю устойчивости по осесимметричной форме, когда образующиеся выпу-чины имеют вид кольцевых складок в направлении координаты λ (перемещения не зависят от λ ).

элементы матрицы ||aij || имеют вид a 11 = R + a cos 9 + w (9) cos 9 — u (9) sin 9, a 13 = a sin 9 + w (9) sin 9 + u (9) cos 9, a21 = _a sin 9+w (9) cos 9_w(9) sin 9_u (9) sin 9_ -u(9) cos 9, a23 = a cos 9 + w (9) sin 9 + w (9) cos 9 + u (9) cos 9 _

-u(9) sin 9, a32 = R + a cos 9 + w (9) cos 9 — u (9) sin 9, a 12 = 0, a22 = 0, a31 = 0, a33 = 0.

Полная энергия деформации будет иметь вид

J = J1 _ PJ2, где

J 1 = 2 п

2 π

Ф 1 ( £ 1 , e 2 , к 1 ,к 2 ) a ( R + a cos 9 ) d9,

J 2 = A V.

£ = A ^{- 1} Bn.

В устойчивом положении равновесия полная энергия принимает минимальное значение. Таким образом, приходим к вариационной задаче

J ^ min , w,u

где функции w, u удовлетворяют условиям периодичности.

Численный метод

Будем аппроксимировать перемещения w ( 6 ) и u ( 6 ) интерполяционными кубическими сплайнами [6]

S ( g ; 6 i ) = g i , 6 i — 2 ni/n, i e [1 : n ] ,

Формула (20) в вычислительном отношении экономична, ибо матрицу A ^{- 1} B необходимо находить всего один раз.

Пусть y e Rm, m — 2n и yi = w(6i), yi+n = u(6i), i e 1: n.

Таким образом, подставляя интерполяционные сплайны в функционал полной энергии, вместо вариационной задачи получим задачу минимизации

^{f (} y ) ^ min ,                 ⁽²¹⁾

y ∈ R ^m

где gi — w(6i) или gi — u(6i).

Сплайн S ( g ; 6 ) для 6 e [ 6 i , 6 i +1 ] задается формулой

S ^{( g ; 6} i ) = g i ^{(1 —} t ^{2 ) 2 (1 + 2} t ) ⁺ g i +1 t 2 ⁽ 3 — ² t ^{) +}

+ m i ht (1 — t ) ² — m i +i ht ² (1 — t ) ,   (16)

где h — 2 n/n , t = ( 6 — 6 i ) /h . В (16) неизвестными являются коэффициенты m _i , которые определяются из условий непрерывности второй производной функции S ( g ; 6 ) в узлах сплайна. Также сплайн должен удовлетворять условиям периодичности, которые приводят к равенствам:

f 0 = f n , f n +1 = f 1 , ^m 0 = m n .

которую будем решать методом сопряженных градиентов [7]. Здесь f (y ) = J(S(w ),S (u )).

Пусть y _k – некоторое начальное приближение. Обозначим

g o =

^{df (} y o ) ∂y

градиент функции f ( y ) . Пусть уже получена точка y k ∈ R ^m . Если

r k = h ^d f ⁽ y^k^ h =0 , ∂y

Таким образом, для определения коэффициентов m 1 , m 2 , ..., m n необходимо решить систему уравнений

{ 2 m 1 + 2 m 2 + 2 m _n — c 1 ,

2 m i- 1 + 2 m i + 2 m i +1 = c i , i e [2; n — 1] ,    ⁽¹⁷⁾

2 m 1 + 2 mn-1 + 2 mn — Cn, где

C i = 2 h ( f i +1 — f i- 1 ) , i e [2; n — 1] ,

C1    2h (f 2 — fn ), cn = 2h (— f 1 + fn-1).

то выполнено необходимое условие минимума, и процесс прекращается. Если же

то на луче

Г к >  0 ,

y k ^{( a} ) = y k ^{— a} g k , ^a >  ⁰ .

Найдем точку y _k ( a ) такую, что

^{f (} y k ^{( a} )) = min ^{f (} y k ^{( a} )) , α >0

где

_ df (yk )   о gk —    гл    + ek gk-1,

∂y

вк = |

0 , k = 0; m ; 2 m ; ...,

r _k ² /r _k ²

1 , k = 0; m ; 2 m ;

..., .

Введем матрицы порядка n.

Если Лебегово множество

A —

B —

\

\

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

D ( y o ) — {y o e R m lf ( y ) 6 f ( y o ) }

.

.

.

.

.

.

,

.

.

.

.

.

.

.

.

.

/

.

.

.

.

.

.

.

.

\

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

/

ограничено, то любая предельная точка последовательности {y _k } , k — 0 , 1 , 2 , ... является стационарной точкой функции f ( y ) на R m , т.е. если y _ks ^ y * при k s ^ 0 , то

r * = h ^df^y*^ h = 0 .

∂y

Кроме того, известно, что метод сопряженных градиентов обладает ”квадратичной” скоростью сходимости [7]. Задача одномерной минимизации на луче решалась методом золотого сечения.

Обсуждение результатов

На рис.1 представлена зависимость максимального перемещения оболочки (ymax = max w2 + u2 – вдоль вертикальной оси) от внеш-i∈1:n i i него нормального давления (P˜ – по горизонтальной оси) при параметрах

R = 200 , a =80 , h = 1 . 28 , P = 1000 _D.

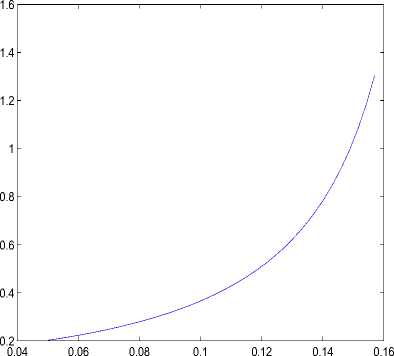
Рис. 1. Зависимость максимального перемещения торообразной оболочки от внешнего нормального давления.

экспериментально получено значение

^ = 0.32 х 10“3, что соответствует давлению P = 11.81. При k = 0.4, a/h = 33, R= 200, a = 80, h = 2.4242,

^ = 0.53 х 10“3, что соответствует давлению P = 37.06. Значение P∗, полученное решением задачи оптимизации (21), равно

P ∗ = 164 . 39 .

При этом отношение

P ∗ /P = 4 . 4357 .

Наконец, при k = 0.2, a/h = 62.5, R = 400, a = 80, h = 1.28

^ = 0 . 3 х 10 “ ³ ,

P ∗ = 32 . 26 , P = 11 . 07 , P ∗ /P = 2 . 91 .

Таким образом, критическое давление, полученное в результате анализа вариационной задачи, от трех до пяти раз превышает экспериментальные значения. Однако при сравнительном анализе рисунков в [8] на стр. 677 можно сделать вывод, что закритическая деформация не является осесимметричной, то есть зависит от угла λ в плоскости параллельного круга. Задача об устойчивости тороидальной оболочки также рассматривалась в работе [9].

Устойчивость сферической оболочки при одностороннем подкреплении

Из графика можно сделать вывод, что вначале перемещение растет линейно с увеличением P ^˜ , а начиная с некоторого значения, максимальное перемещение оболочки резко возрастает. Таким образом, кривая зависимости максимального перемещения от параметра P ^˜ хорошо аппроксимируется гиперболой

F(t) = c1t +c2t+c3 c4t + 1 , где t = P˜ , F (t) – максимальное перемещение. При заданных выше параметрах коэффициенты ci имеют значения

Обозначим через w ( θ ) и u ( θ ) нормальное и касательное перемещения точек оболочки. Декартовы координаты точек сферы будут определяться уравнениями

{

x = ф ( 6 ) = ( R + w ) sin 6 — u cos 6, z = ψ ( θ ) = ( R + w ) cos θ + u sin θ.

Используя формулы (3) , (4) , (7) , (10) , (25) , можно получить нелинейные выражения для деформаций ε 1 , ε 2 и кривизн κ 1 , κ 2 [2]

с 1 = 2 . 6467 , с 2 = 0 . 0554 , с 3 = 0 . 1386 , с 4 = - 5 . 3320 .

Критическим следует считать то значение P ^˜ ∗ , после которого F ( t ) начинает резко возрастать. Из рис.1 видно, что P * = 0 . 13 .

При E = 2 . 05 х 10 6 кг / см ² , v = 0 . 3 критическое давление

_P        0 . 13 D

* = 12(1 - v 2 )1000

0 - 1 ³ E ^Х ₂1 . 28 3 = 52 . 42 .

12(1 - v ² )1000

В работе [8] приведены результаты экспериментов над стальными, жестко закрепленными тороидальными оболочками. В введенных обозначениях

a    (1—v!p k = R, ψ = Eh

e 1 = R ( 2 w — 2 u ) +

+ R 2 ( w ² + u ² + 2 w u + w ² — 2 u w + u 2 ) , e 2 = i (2 w — 2 u cot 6 ) +

1R

+ R2 ^122 — 2wu ctg 6 + u2 ctg 2 6^ , 11

κ 1 =_{1 R} + _RK′ 3 u + w

+     f3 wu — u ² — w ²

_R 2 _K

1          ′′ ′′

+ R2K 1(u w — 2"u к2 = RK 2ww — u + R — 2u ctg 6 —

+ „  ( w ² — wu + uu ctg 6 — 2 wu ctg 6 ) +

R21K

+ ₉— f uw ctg ² 6 + u ² ctg ² 6 — ww ctg 6^) .

R ² K

′′

— R — 2 w +

3 uw + u u

+ w w

_w ′′ _u

В

при

— 2 w' ²) +

′ ^, w ctg θ +

выше приведенных формулах введено обозначе-

ние

k = 0 . 4 , a/h = 62 . 5 , R = 200 , a = 80 , h = 1 . 28

K = ( R ² +2 Rw + w 2 + u ² — 2 Ru — 2 wu ’ +2 uw ‘ + w 2 + u ² ) 1 / ² .

Для вычисления работы внешних сил применим формулы (12) , (13) . Объем оболочки после деформации вычисляется по формуле [3]:

V = П J Ф 2 ( 9,w,u, w ,u ) d9,

где

Ф 2 ^9, w,u,w , u^ = w ³ sin 9 + w ² ^3 R — u ) sin 9 +

+ w uww — 2 Ru + u ² + 3 R2^ sin 9 + R (u ² + uw ) sin 9 +

+ R ³ sin 9 + wuu — w ²

В устойчивом энергия принимает

u ³ + Ruu cos θ.

u — 2 Rwu — u ² w

положении равновесия полная минимальное значение. Таким

образом, приходим к вариационной задаче

J = / F ( 9,w,u,w ,u ,w ) d9 ^ min , ₀                                w,u

где F = Ф 1 — P Ф ₂ . Ниже приведен график зависимости максимального перемещения y max сферической оболочки от внешнего нормального давления P ^˜ при R = 80 , h = 1 . 28 .

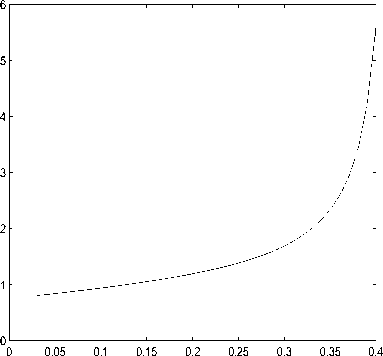
Рис. 2. Зависимость максимального перемещения сферической оболочки от внешнего нормального давления.

Из графика можно сделать вывод, что P˜кр = 0.35, это соответствует при E = 2.05 х 106 и v = 0.3 критическому значению Pкр = 137.79кг/см2 . Теоретическая формула для верхнего критического давления, полученная на основании упрощенной теории тонких 4. пологих оболочек [8], дает значение q в = 1.21E (h/R )2 = 635.008.                   5

Заметим, что там же в [8] на стр.666 указано, что для отношения h/R 6 250 критическое давление следует вычислять по формуле q = 0.3E(h/R)2.

Используя эту формулу, получаем q = 155 . 44 , что да- 6. ет достаточно хорошее совпадение с ранее полученным результатом P кр = 137 . 79 .