Уточнённая модель дисперсии для кварцевого стекла

Кристаллический кварц и кварцевое стекло не что иное, как различные формы диоксида кремния (SiO2). Кварцевое стекло обладает рядом замечательных свойств. Одним из них является устойчивость к резкому перепаду температур. Данный факт объясняется тем, что в кварцевом стекле оксид кремния находится в аморфной форме. Кварцевое стекло имеет очень низкий коэффициент температурного расширения (примерно в 20 раз меньше по сравнению с обычным стеклом) и теплопроводности. В кварцевом стекле содержится очень небольшое количество примесей других химических элементов, а его основу составляет оксид кремния. Поэтому кварцевое стекло обладает очень широким спектром пропускания, малым поглощением света, высокой оптической гомогенностью, стойкостью к ионизирующим излучениям и лазерному излучению высокой интенсивности, высокой рабочей температурой (более 1200 С, что в 4 раза больше, чем для обычного стекла) и т.д. Все эти свойства обуславливают широкое применение кварцевого стекла в оптических науках и промышленности [1–3].

Диоксид кремния имеет различные формы, включая три основные кристаллические разновидности: кварц, тридимит и кристобалит [4, 5]. Кремнезём может также существовать в некристаллической форме в виде кварцевого стекла [4], также он упоминается как аморфный кремнезём и стекловидный кремнезём [6, 7]. Есть четыре основных типа промышленных стёкол кремнезёма. Тип I получается электрической плавкой природного кристалла кварца в вакууме или в атмосфере инертного газа при низком давлении. Тип II производится из кварцевого порошка c помощью газопламенного способа. Тип III является синтетическим и получается путём гидролиза SiCl4 при распылении в кислородно-водородном пламени. Тип IV также синтетический и изготовлен из SiCl4 в паровой плазме, свободной от воды [8,9].

Каждый тип кварцевого стекла имеет свой собственный уровень примесей и оптических свойств. Например, тип I, как правило, содержит металлические примеси [6,7]. При этом типы III и IV намного чище, чем тип I, и лучше пропускают в ультрафиолетовом диапазоне частот [6,7]. Тем не менее тип III имеет более высокое содержание воды, что приводит к высокому поглощению в инфракрасном диапазоне [6, 7, 10]. Тип IV аналогичен типу III, но содержит меньшее количество воды и, следовательно, лучше пропускает в инфракрасном диапазоне [10].

Уточнению коэффициентов преломления и поглощения посвящено множество работ [11–14]. Из результатов экспериментального анализа оптических свойств кварцевого стекла следует, что общепринятая (трёхпараметрическая) модель Селлмейера применима в диапазоне от 0,21 мкм до 7 мкм [15]. При анализе процессов распространения ультракоротких импульсов, длительностью менее 3,5 фс необходимо использовать модель, учитывающую все особенности диэлектрической проницаемости кварцевого стекла. В работе [3] проведён анализ и обобщение большого числа экспериментальных данных, полученных в ходе экспериментов по измерению коэффициентов преломления и поглощения кварцевого стекла, в результате чего были построены экспериментальные дисперсионные «кривые» (облако экспериментальных значений для коэффициентов преломления и поглощения) для кварцевого стекла. Также в работе [3] была предложена модель дисперсии для кварцевого стекла, однако область её применимости охватывает диапазон от 7 мкм до 50 мкм.

В данной работе найдены параметры (резонансные длины волн, амплитуды и коэффициенты демпфирования) модели Селлмейера для более точного согласования (среднеквадратическое отклонение 6%) модельных кривых показателей преломления и поглощения с облаком экспериментальных значений дисперсионных кривых кварцевого стекла, приведённых в [3]. Сравнение результатов моделирования распространения Гауссова (по пространству и по времени) импульса длительностью 3,35 фс и длиной волны 532 нм в волноводах из кварцевого стекла, дисперсия которых описывалась стандартной и уточнённой моделями Селлмейера, показало существенное влияние дисперсии на процесс распространения импульса: высокое поглощение (в 10 раз больше) и замедление

(на 0,35 мкм). Уточнённая модель дисперсии приводит к тому, что фемтосекундный импульс в кварце теряет 90% своей энергии на расстоянии 7 мкм.

1. Модели дисперсии кварцевого стекла

Известно, что от диэлектрической проницаемости возможно перейти к коэффициенту преломления [3]:

n ( x , z , to ) = n Re ( x , z , to ) + i n Im ( x , z , to ) =

= JЁ ( x , z , to ) ,                                                ⁽¹⁾

где n ( x, z, ω) – комплексный показатель преломления; n_Re ( x, z, ω) – показатель преломления; n_Im ( x, z, ω) – коэффициент поглощения, i - мнимая единица.

Для учёта зависимости диэлектрической прони- цаемости кварцевого стекла от частоты излучения используют модель Селлмейера [15]:

Ё (x, z, X) = £_( x, z) +

+ z m

N£ m ( x , z ) 2²

2 ² - x m ( x , z ) - i All m ( x , z )

где λ – длина волны; ε ∞ ( x, z ) – диэлектрическая проницаемость на высоких частотах; Δε m ( x, z ) – величина резонанса; λ m ( x, z ) – резонансная длина волны; η m ( x, z ) – коэффициент демпфирования.

Параметры модели Селлмейера для кварцевого стекла представлены в табл. 1 [15].

Таблица 1. Параметры модели Селлмейера для кварцевого стекла

m	Δε m , мкм	λ m , мкм	η m , мкм
1	0,69616630	0,068404300	0
2	0,40794260	0,11624140	0
3	0,89747940	9,8961610	0
ε ∞ = 1

Формула Селлмейера (2) (с коэффициентами из табл. 1) не только даёт показатель преломления, но и учитывает поглощение на участках, близких к резонансам. Однако в ней только три резонансных слагаемых и отсутствует коэффициент демпфирования, который помогает регулировать величину всплесков вблизи резонансных длин волн. На рис. 1 приведены графики коэффициентов преломления и поглощения, полученных из диэлектрической проницаемости, рассчитанной по формуле (2) с использованием коэффициентов из табл. 1.

Из графиков видно, что оба коэффициента обладают существенными скачками в области трёх резонансов: коэффициент поглощения резко возрастает слева от резонанса, коэффициент преломления падает слева и возрастает справа от резонанса. Однако в работах [3] отмечено, что параметры из табл. 1 применимы только для излучения, находящегося в спектральном диапазоне от 0,21 мкм до 7 мкм. Но для фемтосекундных импульсов длительностью менее 10 фс ширина спектра больше указанного диапазона, и поэтому требуется уточнение модели дисперсии. Для более точного описания экспериментальных дисперсионных кривых [3] для коэффициентов прелом- ления и поглощения в модели Селлмейера (2) были подобраны новые коэффициенты (см. табл. 2).

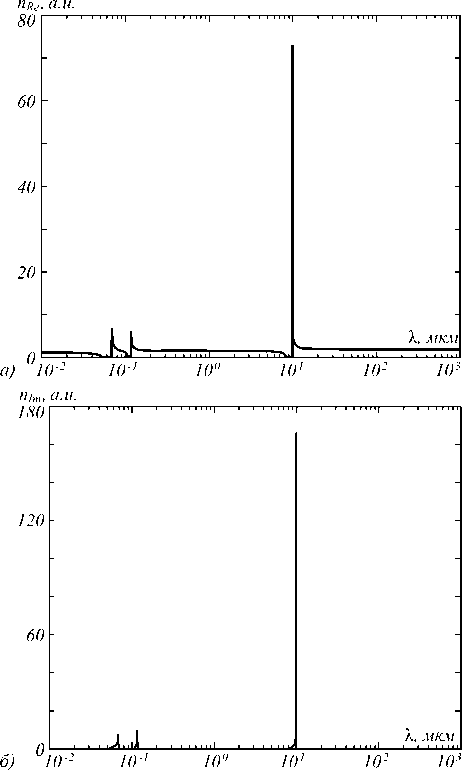
Риc. 1. Зависимость показатель преломления (а) и коэффициента поглощения (б) от длины волны для параметров в табл. 1

На рис. 2 представлены коэффициенты преломления и поглощения, полученные с помощью формулы (2) и коэффициентов из табл. 2. Заметим, что в табл. 2 в сравнении с табл. 1, все коэффициенты отличны от нуля.

Таблица 2. Новые параметры модели Селлмейера для кварцевого стекла

m	Δε m , мкм	λ m , мкм	η m , мкм
1	0,60616630	0,067404300	0,028
2	0,16	0,0983	0,017
3	0,440794260	0,11624140	0,01
4	0,59747940	9,04616108	0,35
5	0,00520045	12,6739082	0,05
6	0,75	22,1243678	1,8
ε ∞ = 1

Табл. 2 учитывает шесть резонансов дисперсионной кривой для кварца, и график на рис. 2 более точно отражает экспериментальные данные [3]. Среднеквадратическое отклонение построенных модельных кривых от облака экспериментальных данных составляет около 6%, в то время как среднеквадратическое отклонение для классической модели Селлмейера составляет 37%.

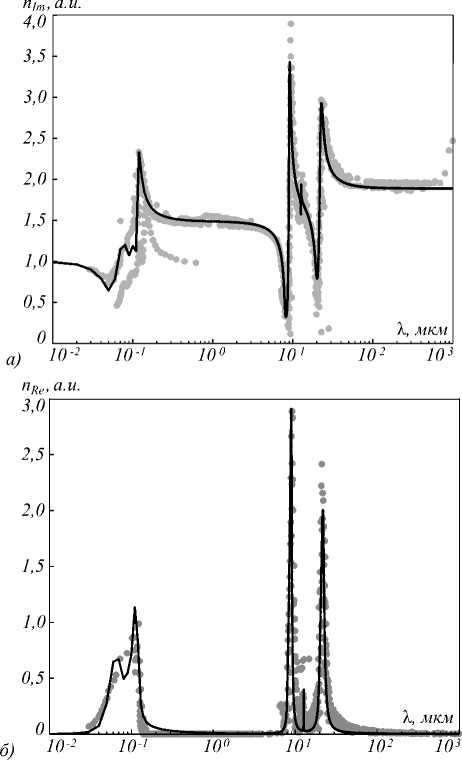
Риc. 2. Зависимость показателя преломления (а) и коэффициента поглощения (б) от длины волны для уточнённой модели Селлмейера (табл. 2) и «облако экспериментальных данных»

Моделирование проводилось с помощью пакета FullWave. Для моделирования были выбраны следующие параметры: l x = 1 мкм, l z = 15 мкм, T = 100,1 фс (время моделирования), h x = λ 0 /266 мкм, h z = λ 0 /354 мкм, h t = λ 0 /886 (шаги дискретизации) [16, 17] . На рис. 4 приведена зависимость интенсивности импульса от времени в точках ( x, z ) = (0, 3) мкм и ( x, z ) = (0, 7) мкм, полученная после распространения ультракороткого импульса вида (3) длительностью 3,35 фс внутри волновода из кварцевого стекла. Ошибка в расчётах составила 0,004λ₀.

2. Влияние модели дисперсии на процесс распространения ультракороткого импульса

Определим влияние уточнённой модели дисперсии на распространение ультракороткого импульса. Для этого промоделируем распространение Гауссова импульса в планарном волноводе из кварцевого стекла шириной l x и длиной l z , дисперсия которого описывается моделью Селлмейера (2), используя сначала параметры из табл. 1, а потом из табл. 2. Начальный импульс зададим следующего вида:

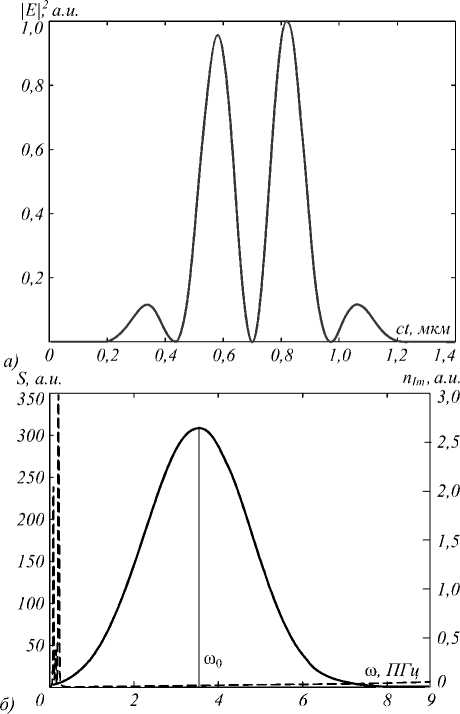
Риc. 3. Интенсивность |Ey|2 (а) и амплитуда спектра S (б)

V ( x, t ) = exp

x

^^^^^^s

a

• exp

I

t ts

^^^^^^s

td

sin ( to ₀ 1 ) ,

где a = w /2; w – ширина волновода; t s – время импульса по полуспаду интенсивности; t d – время задержки; ω 0 = 2π с/ λ 0 – несущая частота; с – скорость света в вакууме; λ 0 – несущая длина волны.

Зададим параметры входного излучения для моделирования: w = 1 мкм, t_d = 6,67 фс; t_s = 1,17 фс, λ₀ = 0,532 мкм. На рис. 3 представлен начальный импульс и его спектр.

входного Гауссова импульса (сплошная линия) длительностью 0,7 фс в точке (x,z)=(0,0) мкм, коэффициент поглощения (пунктирная линия)(табл. 1)

Из рис. 4 видно, что максимальная интенсивность импульса, распространяющегося в волноводе из кварцевого стекла, диэлектрическая проницаемость которого описывается классической моделью Селлмейера (линия 1), больше максимальной интенсивности импульса, распространяющегося в аналогичном волноводе, дисперсия которого описывается уточнённой моделью Селлмейера (линия 2), в 3,3 раза в точке ( x, z ) = (0, 3) мкм и в 9,5 раз в точке ( x, z )=(0,7) мкм. Также необходимо отметить большее запаздывание импульса, распространяющегося в волноводе, дисперсия которого описывается уточнённой моделью (табл. 2): в точке ( x, z ) =(0, 3) мкм импульс отстаёт на 0,35 мкм, а в точке ( x, z )=(0,7) мкм – на 0,32 мкм.

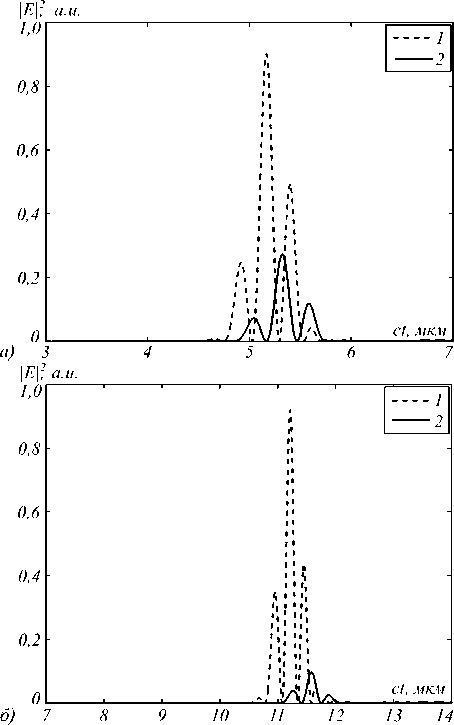
Рис.4. Временная зависимость интенсивности импульса в точках (x,z) = (0,3) мкм (а) и (x,z) = (0,7) мкм (б), полученная с учётом частотной дисперсии с помощью модели Селлмейера и табл. 1 (линия 1) и табл. 2 (линия 2)

Импульс, распространяющийся в волноводе из кварцевого стекла, диэлектрическая проницаемость которого описывается классической моделью Сел-лмейера, движется в 1,5 раза медленнее скорости света, в то время как импульс, распространяющийся в таком же волноводе, дисперсия которого описывается уточнённой моделью Селлмейера, движется в 1,58 раза медленнее скорости света.

В процессе анализа результатов численного моделирования сравнивались поглощательные способности кварцевого стекла, получаемые за счёт использования разных моделей. При преодолении импульсами расстояния в 3 мкм в первом случае поглотилось 6,4% энергии, в то время как во втором случае (уточнённая модель) – 69% энергии. На расстоянии в 7 мкм в первом случае – 8,5%, а во втором – 87,5%. Поглощение фемтосекундного импульса в кварцевом волноводе с обычной дисперсией в 10 раз слабее, чем в волноводе с уточнённой дисперсией.

Исходя из полученных данных, можно сделать вывод, что в процессе моделирования распространения ультракоротких импульсов в кварцевом стекле необходимо максимально точно учитывать зависимость диэлектрической проницаемости от частоты. В противном случае полученные результаты могут расходиться как в количественных, так и в качественных характеристиках: максимальной интенсивности, энергии импульса и времени появления.

Заключение

В работе получены следующие результаты:

– найдены параметры (резонансные длины волн, амплитуды и коэффициенты демпфирования) модели Селлмейера (2) для более точного согласования (среднеквадратическое отклонение 6%) модельных кривых показателя преломления и коэффициента поглощения с облаком экспериментальных значений дисперсионных кривых кварцевого стекла;

• –    сравнение результатов моделирования распространения Гауссова (по пространству и по времени) импульса длительностью 3,35 фс с длиной волны 532 нм в волноводах из кварцевого стекла, дисперсия которых описывалась стандартной и уточнённой моделями Селлмейера, показало существенное влияние дисперсии на процесс распространения импульса: высокое поглощение (в 10 раз больше) и замедление (на 0,35 мкм) за 7 мкм;

• –    фемтосекундный импульс теряет 90% энергии в кварце на расстоянии 7 мкм.

Работа выполнена при поддержке грантов РФФИ (13-07-97008) и (14-07-31218).