Уточнённый метод аппроксимации равноамплитудных полиномов

Оренбургский государственный университет

В работе показана недостаточная эффективность применения современных источников измерительных сигналов для измерения частотных характеристик в области инфранизких частот. Предложен к применению сигнал на основе тригонометрического полинома с равномерным дискретным спектром и метод его аппроксимации. Получены аналитические выражения дискретного гармонического спектра аппроксимирующей функции. Предложена методика оценки погрешности аппроксимации в виде коэффициента гармоник паразитного спектра и неравномерности амплитудного спектра в рабочей области частот.

В процессе разработки, производства и эксплуатации отдельных образцов радиоэлектронной аппаратуры и средств телекоммуникаций остаются востребованными измерение, контроль и идентификация их частотных характеристик (ЧХ) в диапазоне от инфраниз-ких частот до нескольких десятков герц [1].

Ручные высокоточные методы анализа частотных характеристик (ЧХ) малопроизводительны, и в указанном диапазоне потребуют значительных трудозатрат – до нескольких десятков человеко-часов.

Самая низкая анализируемая частота современных автоматизированных измерителей амплитудно-частотных характеристик (АЧХ), в которых в качестве источника испытательного сигнала используется генератор качающейся частоты (ГКЧ), ограничена величиной 20 Гц [2]. Ограниченность применения таких устройств на низких частотах связана с тем, что спектр испытательного сигнала на выходе ГКЧ – частотно-модули-рованного импульса – неравномерен в полосе качания. Известно, что степень неравномерности спектральной плотности одиночного линейно частотно-модулированного (ЛЧМ) импульса напрямую связана с величиной так называемой базы [3]

B =∆ f ⋅ τ и , (1) где Δ f – девиация частоты ЛЧМ-импульса или ширина полосы измерения АЧХ; τ_и – длительность ЛЧМ-импульса.

С увеличением величины базы B спектральная плотность ЛЧМ-импульса становится более равномерной в полосе качания [3]. Из выражения (1) следует, что для улучшения равномерности спектра с той же шириной полосы качания необходимо увеличивать длительность ЛЧМ-импульса. Для одного из лучших измерителей АЧХ [2] Х1-41 минимальная величина ширины полосы качания – 100 Гц, нижняя граничная частота полосы - fн =20 Гц, максимальное значение длительности рабочего хода развёртки (длительности ЛЧМ-импульса) – 10 с. Соответственно, величина базы не превысит значения B=1000, при котором обеспечивается паспортная величина неравномерности уровня выходного напряжения ГКЧ δU =0,5 Дб, или 5,92%. Для измерения ЧХ на более низких частотах неизбежно встанет необходимость сужения полосы качания. Для сохранения или улучшения той же равномерности напряжения на выходе ГКЧ необходимо обеспечить величину базы B ≥ 1000 , то есть, в соответствии с (1) – увеличить длительность ЛЧМ-импульса τи . Для измерения ЧХ на частотах f ≤ 20 Гц потребуются величины τи от сотен до нескольких тысяч секунд. То есть для измерения потребуется время, соизмеримое с временными затратами в ручных методах, а в структуре измерителя АЧХ потребуются дополнительные устройства стабилизации внутренних параметров измерителя для уменьшения влияния внешних дестабилизирующих факторов – колебаний температуры, влажности, напряжения внешней питающей сети и так далее. Кроме того, ЛЧМ-импуль-сы, другие частотно модулированные сигналы имеют ненулевой нелинейный фазовый спектр, что делает их малопригодными для измерения фазо-частотных характеристик.

Кроме ЛЧМ-сигналов в современных измерителях ЧХ в качестве зондирующих сигналов применяются импульсные сигналы с короткой длительностью прямоугольной или произвольной формы [4, 5], а также многочастотные сигналы [6, 7].

Спектральная характеристика известной дельта-функции бесконечна и постоянна [3]. Импульсные сигналы короткой длительности стремятся приблизить к свойствам дельта-импульсов, однако в виду бесконечности амплитуды дельта-функции полностью они им соответствовать не могут. Например, форма спектральной плотности одиночного прямоугольного импульса (рис. 1) короткой дли- тельности τи от идеальной равномерности далека, и для измерения ЧХ в области низших частот с точностью до 5% пригодна лишь часть главного лепестка спектра импульса – диапазон частот

A f = 0,...,0.17 • -1

τ ^, и

при этом энергия испытательного сигнала используется неэффективно. Для повышения точности измерения ЧХ в том же диапазоне необходимо уменьшить длительность импульса, а соответственно и увеличить скваж-

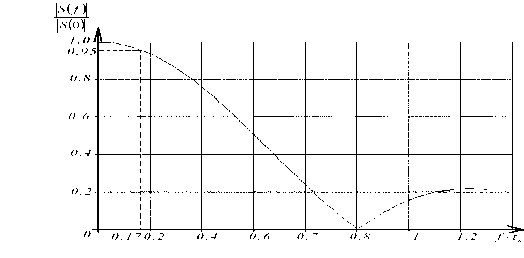
Рис. 1. Форма спектральной плотности одиночного прямоугольного импульса ность импульсного сигнала, что потребует увеличения требований к точности задания длительности τии его долговременной нестабильности.

В некоторых измерителях ЧХ, использующих зондирующие импульсные сигналы произвольной формы, для измерений используют более широкий участок спектра, то есть и участок, где его относительная неравномерность далеко превышает требуемую точность измерения. Но в таком случае используется дополнительная операция нормирования спектра [4, 5] сигнала, принятого с выхода исследуемого объекта, а в конструкции измерителя ЧХ необходимо предусматривается дополнительное запоминающее устройство с информацией о спектре испытательного сигнала.

Измерители ЧХ, использующие многочастотный сигнал – суммарный сигнал с выходов нескольких синхронизированных генераторов гармонических сигналов разных частот, пригодны для измерения в ограниченном диапазоне частот. Кроме того, для изготовления одного синусоидального генератора инфранизкой частоты требуются реактивные элементы (в основном конденсаторы) с большими значениями параметров, а соответственно и габаритных размеров, а также дополнительное устройство стабилизации частоты и амплитуды [6]. Таким образом, структура многочастотного генератора в области инфранизких частот получится очень громоздкой и ограничена в плане универсальности применения.

Поэтому для усовершенствования измерителей ЧХ в плане снижения трудоёмкости, повышения производительности измерений с сохранением приемлемой точности предлагается использовать в качестве генераторов испытательных воздействий генераторы равноамплитудных полиномов – функций, разлагающихся в тригонометрический ряд Фурье с одинаковыми амплитудами и нулевыми начальными фазами [8].

При вычислении значений полиномов применяются операции умножения и деления, поэтому для реализации их генераторов требуются устройства умножения и деления.

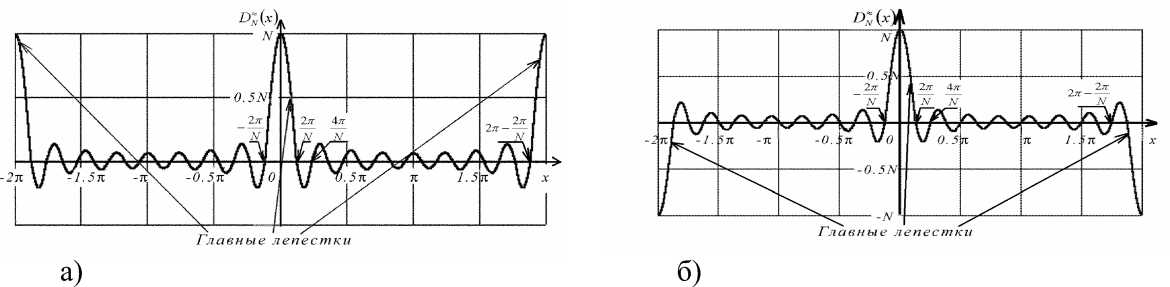
Рис. 2.

Но в виду наличия в полиномах точек с неопределённостью вида “ноль на ноль” реализация генераторов на аналоговых схемах невозможна.

Один из вариантов решения задачи генерации полиномов – разработка метода аппроксимации равноамплитудного полинома. В настоящей работе предлагается метод аппроксимации функции sin (Nx)

D n ( x ) =     ² , N = 3,4,         ₍₃₎

sin ( 2 )                ^{,       (3)}

который представляется ограниченным косинусоидальным рядом Фурье [8]

D n ( X ) = ^

0.5 ( N -1 )

• 1    + 2 £ cos ( n • x ) при нечётных N, n =1

0.5 N

• 2    £ cos ( ( 2 n - 1 ) X ) при четных N .

n =1

В работе [9] одним из авторов предложен вариант несложного метода аппроксимации равноамплитудного полинома (3). Однако количественные и качественные характеристики дискретного спектра аппроксимирующей функции в предложенном методе невысоки – коэффициент гармоник паразитного спектра k_{г , N} превышает 5%, а максимальная величина относительной неравномерности основных гармоник приближается к 10%.

В настоящей статье предлагается уточнённый метод аппроксимации, суть которого в следующем:

• 1)    Главные лепестки – отрезки кривых функции (1) на промежутках

X e(- 2n + П,2п + 2л/) j e Z, (5) и несколько k < N-2 соседних пар полуволн функции (1) (рис. 1) для x e (- ^nN±i) + 2n/,-ini + 2/о [n + 2nj, П+П + 2nj) i1 = 1, ^, k; j e Z

(6) аппроксимируются произведением гармонических функций

H ni = cos ( Nx ) • cos ( Nx ) • ^ • cos (^ x ) = П cos ( ^X ) ^{x 4 8} 4 ^ 2 ^l ’ i '=o 4^ 2

Здесь Z в выражениях (5) и (6) – множество целых чисел, l в выражении (7) – порядок произведения. На интервале (5) функция (3) аппроксимируется с помощью выражения

D2N,i,fc (x) = (-1)j(N+1) • N ■ nN,, (x - 2П), (8) а на интервале (6) – с помощью выражения m - zY x (-1)j(N+1)" Dn (x 0n )„ /   ..x

D 2 , ( x ) =------------, ----x----- П м 7 ( x - 2nj )

• ^N ■ l ,'          H n ,i ( x0 1 )         ^N ,^{Л       J)}’

(9) где x 0 _{i 1} – локальный экстремум i1- й полуволны.

• 2)    На остальных интервалах:

x e (- 2N> + 2nj,- 2ni + 2nj] о [2ni + 2nj, ^ + 2nj), i=k+1,_, N - 2; jeZ,

(10) полином (3) аппроксимируется полуволнами синусоидальной функции

D 2 N , i , k ( x ) = ( - 1 ) ^{( N + 1 )} • D n ( x 0 i |). sin (^)

x 0 i =

n ( 2 i + 1 ) N

Общее выражение для аппроксимирующей функции примет вид

■ (-l) ^{j (} N ^+l). ( - l) ^{j (} N ^{+ l )}

^{П (} j ^N'^X , ^{g (} - N ^П )

,'V "- ⁽ ) 'X J- t ² ^^     ■ ')

⁽ x ⁰ . l )

^ПN , l

( - l) ^{j (} N ^{+ l )}

=

^D2Nlk ( * ) = 1

d n ⁽ x ⁰ . 1 H N j |xj |^- [^ ni ,     ⁺ )

Xj= x - 2nj, j c Z, il = 1...k, i = k + 1...f, x0. = N, x0i, - il - й локальный экстремум.

Локальные экстремумы x 0 _{i 1} в выражениях (9) и (12) получены следующим способом:

• 1)    Для функции (3) изменён масштаб аргумента в N раз

D (- j ₌ sin⁽ 2 ) у 34

D N ⁽ N ) Sin (, N ) ^, "   3 ^ .      ^(l3)

Длительность каждой полуволны A x теперь не зависит от N

A x = 2 n'

от N зависит период повторения, а точки локальных экстремумов при разных значениях N, как показал вычислительный эксперимент в программной среде MatchCad, достаточно близки.

• 2)    Выражение для первой производной функции (11) имеет вид

dD N ⁽^ ' = N co ^{s ( x ) sin (} N ^{)- sin ( x} ) ^{cos (} N )

dx                 N sin ² ( NN )            . ^(l4)

• 3)    В программной среде MathCad решено уравнение

f ( x ) = N cos ( x ) sin ( n ) - sin ( x ) cos ( n ) = 0 (15) для i1=1…3 для N=6…200 относительно x , после чего получены корни X 0 _{i 1, N} . Точность методов решения уравнения (15) такова, что величина абсолютного отклонение производной (14) от нуля не превышает значения io ^{- 13} .

• 4)    Соответствующие точки экстремумов не масштабированной функции (3) для каждого N пересчитаны при помощи выражения x 0_й , n = ^^ ^^N .             (16)

Эксперимент в программной среде MathСad показал, что с ростом порядка про- изведения l погрешность аппроксимации главного лепестка и нескольких k соседних пар боковых полуволн уменьшается при условии, что k не превышает значения 21 -1, так как для следующих полуволн характеры поведения функции произведения (7) и аппроксимируемой функции (3) существенно различаются. Применение модели (12) при l >2 нецелесообразно, так как потребует непропорционально большего количества аналоговых умножителей при схемотехнической реализации. При l=2 и k=3 значение относительного, приведённого к N отклонения

A N , , , . ( x ) = tz^ k l N Z D N A , |oo-% (17)

не превышает 0,4%, что более чем на порядок меньше, чем при аппроксимации предыдущим способом [9].

Меньшее значение погрешности аппроксимации должно снизить степень отличий спектральных свойств аппроксимирующей функции (12) полинома (3). Особый интерес представляют следующие отличительные особенности дискретного спектра модели (12):

• 1)    степень неравномерности амплитудного дискретного спектра модели (12) в рабочей области – на частотах, для которых определён спектр полинома (3) или (4);

• 2)    отличие от нуля значений фазового спектра для тех же частот;

• 3)    количественные характеристики новых “паразитных” гармоник.

Для оценки указанных характеристик необходимо рассчитать дискретный спектр функции (12). Так как полином (3) на промежутках (5), (6) и (10) аппроксимируется функциями разного вида, то определение спектра целесообразно выполнять, придерживаясь следующей последовательности:

• 1)    определить выражения спектральных плотностей одиночных аппроксимирующих функций каждого интервала в выражении (12) для множества x e ( - 2 n ,2 n ) — то есть для кривых одного периода колебаний функции (12) при чётных значениях N и для двух периодов при нечётных N ;

• 2)    приняв за величину периода повторения одной аппроксимирующей кривой выражения (12)

T = 4п, определить выражения для комплексных амплитуд гармоник её дискретного спектра как выборки из соответствующего выражения спектральной плотности на частотах, кратных частоте первой гармоники [10]

2 π 1

^го 1 = у - 2;             (18)

• 3)    воспользовавшись принципом суперпозиции для каждой гармонической составляющей спектра сложить все полученные выражения для её комплексной амплитуды. Несмотря на то, что для нечётных значений N величина периода Т избыточна – действительный период повторения в этом случае в два раза меньше, величины амплитуд “новых” гармоник с частотами го = го ₁ , го 3 , го 5 , . будут равны нулю, и останутся лишь гармоники с частотами, кратными реальной частоте повторения 0.5 го, = 1.

Итак, определим спектр функции (12).

• 1)    Определение спектра главных лепестков на интервалах

X ^е ( - N + ⁴ п ■ j, N + 4 п ■ j )         (19)

и

X g (2n(2j - 1),2п(2j -1)+ n)и и (2п(2 j +1)- N ,2п(2 j -1)), j 1 g Z. (20)

• а)    Выражение спектральной плотности на промежутке (20) при j=0 примет вид

2 π

So (го ) = 2 N fH cos(Nxr )cos(гox) dx (21) 0 -=oV2

Произведение (7) представляется конечным рядом Фурье

П                     ) - —У c ^{( 2} ” '^{-1 ) Nx} )

Un, 1 (x) И cos(4.2-/ ni ^ cos( 421 ) . (22) i=0       42       2 n '=1

В связи с этим выражение (21) преобразуется к виду

N (21       (           \1

S ₀ ( го ) = 2 N № cos ( ( 2 n ^^)cos ( гox ) f dx =

2 0 I nM       ' 4-21 'I

. ( _ , ,A_Ar - ⁽2 n -1) п      2 пго     V+^{2        (}2 n -1) n . 2 пго

2 ¹ 12 n -1 I N sin—,,, cos ^7- - 2    го cos—,, / sin —xr-

ZX /        1 l + 1        N                   il + 1

• б)    Выражение для комплексных амплитуд составляющих дискретного спектра главного лепестка определим, сделав выборки из выражений спектральной плотности (23) для частот, кратных частоте первой гармоники [10] го = пго ₁ , n = 1,2,(24) и для _го = 0 . Для n- й гармоники это выражение примет вид

2 S о ( и_Ю 1 )

0, n

(" ⁽² n ' ^{- 1} ) ^П nn       -^{1 +1        ( 2} n ' ^{- 1} ) ^п - nn

4 N 2 (2 n-1)N sln^T+^cos N - n 2 c-s 2 .■ si- NT

П n ' = 1                   ( 2 n ' - 1 ) N - 2 n

Для значений N, кратных 21+1 для гар- моник с номерами n <

2 ^{1 + 1} - 1) N

2 - 2 ¹

найдётся некоторое число p, при котором выполниться равенство

_ (2-p-1)N n       21+1   , p = 1,...,21.

Составляющая суммы с номером p в выражении (25) преобразуется к виду f n ЙЛАо’п (2 p-1')П nn

4 N ^{( 2 p - 1 ) N sin} .1 - 1 ^cos NT lim                        ²

-^2^ n    ( 2 p - 1 ) ² N² - 2 ^{2 1 + 2} n²

n ^{2 1 + 1} c ^os ( 2^ ^sin ^ Nn 1 _ 1 ₊ N sin ^ Nn

( 2 p - 1 ) ² N² - 2 ^{2 1 + 2} n²      2 ¹ + 2 ^{1 + 1} n , ⁽²⁷⁾

а выражение (25) следующим образом

A'n

0, n

Для чётных значений N постоянную составляющую аппроксимирующих функций каждого интервала выражения (12) вычислять не имеет смысла, так как функция (12) при этом нечётная и результирующая постоянная составляющая спектра примет нулевое значение.

в) Отрезки главных лепестков на промежутке (20) при j=0

x e ( - 2 п , - 2 п + N ) и ( 2 п - 2n ,2 п ) . (30) симметричны относительно оси Oy , поэтому их спектральная плотность определится как удвоенная действительная часть спектральной плотности одного из отрезков. Отрезок для левой части промежутка (30) можно получить параллельным переносом половинки лепестка на промежутке x e ( 0, 2 п ) вдоль оси Ox на - 2 _П . Согласно теореме запаздывания выражение спектральной характеристики для множества (30) примет вид

_{2 l} 2 _N π

S g ( to ) = ( - 1)^* 2 N e 2 ^пш Z f cos ^{( 2} "⁴*^Nx cos ( to x ) dx = 0                               il                               4 * 2

²              " '=1 0

c^±fo⁴             Э sin ⁽ 2 " L1 ⁿ

= ^S 0 ^{( 0 )} = ( - 1) N + 1 2 Z       2 ^{l + 1}   =

T               к n =1 2 n ' - 1

• д ) Выражения для составляющих суммарного спектра лепестков:

• -    для постоянной составляющей для нечётных значений N :

A 0,0 = A'„ + A 1. = ( 1 - ( - 1 ) N K- = 2 • A'„ ;(34)

• -    для комплексной амплитуды n- й гармоники:

8 N ( - 1 ) ^{N + 1}

2 ^l Z n ' = 1

' ^{( 2} n ' - 1 ) ^N sin (( I n ^ ^{- 2} to ^{П ) cos}    "

( 2 n '- 1 ) 2 N ² - 16 • 2 2 ^l to ²

A„ = A* + A ± = ( 1 - ( - 1 ) N ⁺ n )a* . (35) 0, n            0, n        0, n                                     0, n .

• 2)    Определение спектральной характеристики отрезков функции (12) на промежутках

x e ( - ^ h¹ ) + 4 n • j , - 2Ni1 + 4 n • j ] u

u [2 ni l + 4 n • j , ⁿ + ¹ + 4 n • j ) ,    (36)

x e ( - 2 n ( 1 - 2 j ) + N , - 2 n ( 1 - 2 j ) + 2^ ] и u [ 2 n ( 1 + 2 j ) - ^{2 n} ( N + l ⁾ ,2 n ( 1 + 2 j ) - ²4 ), i1 = 1 _ k .

• а) Выражение спектральной плотности на интервале (36) при j=0 имеет вид

+

5 1 ( to ) =

2 D N ⁽ x 0 . , )

2 l + 2 to sin ( 2 nto ) - 2 l + 2 to cos^ ^ r+ r ¹ ) - 2to ) n ) sin^ Лт

⁺              ( 2 n '- 1 ) 2 N² - 16 • 2 ^{2 l} to²             _v

n Nl ^{( x} 0 . 1 )

N ⁽r⁺¹⁾_n             8| D N ⁽ x 0 1 ⁾_х

J n N i ( x ) cos ( to x ) dx = —--- j ----г x 2 ^П . 1    ’                          n N , l ⁽ x ⁰ . 1 )

г) Выражения составляющих дискретного спектра на интервалах (20):

- для комплексной амплитуды n-й гармоники

/ РГ^<ч11 ^{2 n} 1-1- ^to Vrf^jl -I- 1 ПЧ1П II^{2 n 1} -I- ^to J77" I 2 l , I ^cos((^ l + T ⁺ NПх^{2 1 +} ^sin((^ l + T ⁺ NП )

^Z I            ( 2 n ’- 1 ) N + 4 • 2 ^l to

+

A ±

0, n

2 S 0 ^{( n to} , ) = ( - 1 ) N + n + ! ^{4 N} *

Tπ

2 ^l

*Z

n ' = 1

( ( 2 n ’- 1 ) N sin I² " -* cos ™

2 ^{l + 1} N_

( 2 n ’- 1 ) ² N² - 2 ^{2 1 + 2} n²

^{l +1} cos⁽² " '-^{1 П} sin ™ " 2 ^cos ₂ 1 + 1 ^sin N

( 2 n '- 1 ) 2 N² - 2 ^{2 1 +2} n²

= ( - 1 ) ” ⁺ " + ' A‘ 0, , .

2 n ' - 1 to L/Qj-l । 1           2 n ' - 1 to L I

, ^Co s ((^ l +2 - N П\2 ^{г 1 +} ^sin ((^ l n - N П ) ⁺             ( 2 n ’- 1 ) N - 4 • 2 ^l to            * .

б) Выражения составляющих дискретного спектра на интервалах (36):

- для постоянной составляющей для нечётных N :

f X cosl⁽2²¹⁺¹⁾⁽2 n '-!) n Lin ^{(2 n} '^-1) ⁿ A ,      S . 1 (0) ⁴ • D N ⁽ x 0 , 1 ) ,²Л ^co0 2 1 + 2     /^Sin^ T +T- ;

, ^T       n N • n N , l ^{( x} 0 , 1 ) " '=1               ² n ^1-1               ’

(39) - для комплексной амплитуды n- й гармоники:

- для постоянной составляющей для

нечётных значений N :

A '-!

1, n

2 S„ ( "to 1 ) = 4 D , ⁽ x 0 , 1 ) _x T        ПП . , l ( x 0 , 1 )

2 ^l х ^ _и ‘ = 1

2n'-1 n )^(2-i 1+1))sinH2”'-1

^COS\\ ₂ . ₂ 1 ⁺ N)   2 Г  \\_{2 - 2} 1 ⁺ N /2/

(2 n '-1) N + 21+1n

+

2n'-1     ” )n(2.1+1)kinH2”'-1

^CO s\\₂ . ₂ 1     N) 2 /sin\\₂ . ₂ 1     N /2 ) I

( 2 n ’- 1 ) N - 2 ^{1 + 1} n           I . ⁽⁴⁰⁾

Для N, кратных 2 ^{1 + 1} , для гармоник с номерами n , удовлетворяющих условию (26), после определения предела для соответствующих членов суммы в выражении (40), преобразуем выражение (40) к виду

A^' i1,n

n _ ( 2 p - 1 ) ^N 2 - 2 ¹

' cos sin ^K ₊ п ₊

2 ^{1 + 2} n          2 ^{1 + 2} N

2 ^l

+ Z | n S

cos ( ( 2 n .¹ + n ) ^{n (2}^ ) sin I ( 2 n ' ^- 1 + n ^- )

W 2 . 2 1 N / ² /      \\ 2 . 2 1 N /2 )

+

( 2 n ’- 1 ) N + 2 ^{1 + 1} - n

COsll 2 n '- 1 n ^{— (2-}*¹⁺¹⁾ Tll|2 n '- 1 n K O jin / Л M ₊ ^cos W 22 1 ^- N           \⁽ 2 2 1 - N Г2 1    4| D N ⁽ X 0_n)

( 2 n '-1 ) N - 2 ^{1 + l} - n        | J п П , , , ( x 0,, ) •

(41) где p удовлетворяет условию (26).

• в)    Отрезки кривых модели (12) для множества (37) симметричны оси Oy и их можно получить аналогичным параллельным переносом, что и отрезки кривых на множестве (20). Поэтому выражения для составляющих дискретного спектра множеств (36) и (37) будут обладать свойством, аналогичным свойствам (19) и (20):

• -    для постоянной составляющей для нечётных значений N:

A , 1 , o _ ( 1 - ( - 1 ) N ) A i 1,0 _ 2 A (42)

• -    для комплексной амплитуды n- й гармоники:

• A , 1, . _ ( 1 - ( - 1 ) N ⁺ " ) A „. . .           (43)

Показанное свойство справедливо и для спектральной функции всех остальных отрезков аппроксимирующей модели (12).

• 3) Определение спектральной характеристики отрезков функции (12) на промежутках

x e ( - 2Ф¹ ) + 4 п - j , - 2Л. + 4 п - j ] u

u [ Ni + 4 п - j ,^№ + 4 п - j )       ⁽⁴⁴⁾

x e (- 2п(1 - 2 j) + 2п ,-2п(1 - 2 j) +     ] и и [2п(1 + 2 j)- П+1) ,2п(1 + 2 j)- 2n), j e Z, где

Г 1,..., ( 0.5 N - 1 ) при чётных N ,

[ 1,..., ( 0.5 ( N - 1 ) - 1 ) при нечётных N .

• а)    Выражение спектральной плотности на интервале (45) при j=0

2 ( i + 1 ) -

N

S i ( ю ) _ 2 D N ( x 0 i ) j sin ( N 2 ^X ) cos ( tox ) dx _ 2 πi

N

( - 1 ) i 8 d n ( x 0 , ) N

cos ( ² ‘ ⁺N^-® cos ^ю N² - 4 to²

При № _ 0,5 N спектральная плотность примет значение

Kto ⁽ 2 i ^{+1 )} пю

S ( ю _ N ) _ ( - 1 ) I d ( x 0 ) 8 N lim ^cos       cos N _ 0

2       N          22     .

ю ^ N N - 4 ю

• б)    Выражения для составляющих дискретного спектра на интервале (45):

• -    для постоянной составляющей при нечётных значениях N :

  A ^'

  ,0

  
  

S , (0) _ ⁽ - ^{1 ) 1} 21 D N ⁽ x 0 , ) ^N _ ^(- 1 ) ' ²| D N ⁽ x ⁰ , ⁾|

T           πN ²              πN

- для комплексной амплитуды n- ой гармоники:

A ' _ S , ⁽ n№ 1 ) _ ^(- 1 ) ' 4 dn ^{( x} 0 , ) N cos ⁽²' + NN^- cos f N .

' • ”       T                 k ( N² - n ²)          ^;

• -    для гармоники с номером n=N:

A i , n _ 0.                (50)

• в)    По аналогии с выражениями (34)-(35) и (42)-(43) выражения для составляющих

суммарного дискретного спектра -ых полуволн на интервалах (44) и (45) примут вид:

• -    для постоянной составляющей при нечётных N:

A , 0 _ ( 1 - ( - 1 ) N ) A i ,₀ _ 2 A ' ,, ;      (51)

- для комплексной амплитуды n- й гармоники:

A„ = ( 1 - ( - 1 ) N + ■ ) a i , n ;          (52)

• -    для составляющей с номером n=N :

A i,N = 0 .                     (53)

• 4)    Спектральная характеристика “хвостов” - отрезков кривых функции (12) для нечётных значений N на интервалах

x e (- n + 4n • j,-n + N + 4n • j] и u[n - N + 4n • j, П + 4n • j)     (54)

и x e(- n(l - 4 j) - N ,-n(l - 4 j)] U .

u [ n ( 1 + 4 j ) ; n ( 1 + 4 j ) + N ), j e Z .    (55)

• а) Спектральная плотность пары “хвостов” на интервале (55) при j=0:

S_k ( ® ) = 2 • J sin ( Nx "j^ dx =

π

П

N

= 4 • ( - ₁ ) 0.5 ^{( N + 1 )} •

2 ® sin ( n® ) - Ncos ( n® - 5® )

, (56)

N ² - 4 ® ²

где k = 0.5 ( N - 1 ).

При _ю = 0.5 N

S k ( ® = NN ) = к

A k , n = ( 1 - ( - 1 ) N ^{+ n} ) A ' k , n = ( 1 + ( - 1 ) ⁿ ) A ' k , n ; (62) - для составляющей с номером n=N :

A k , n = 0.                  (63)

• 5)    Выражения составляющих общего дискретного спектра функции (12):

• а)    Для постоянной составляющей:

• - для чётных значений N :

a 0 = 0;

- для постоянной составляющей при нечётных значениях N :

k             0.5 ( N - 1 ) - 1

^A 0 = ^A 0,0 ⁺ E ^A i 1,0 ⁺ E ^A i ,0 ^{+ A} k ,0 . (64) i 1 = 1                   i = k + 1

• б)    Для комплексной амплитуды n- й гармоники

• -    при чётных значениях N для n ^ N :

k             0.5 N - 1

A = A„ + TA, + TA. •

• n           0,n               i1,ni

i 1=1

• -    при нечётных значениях N для n ^ N :

k              0.5 ( N - 1 ) - 1

A = A_n + TA, + TA. + A_n^„,. ■ n          0, n               1 1, n                    i , n          0.5 ( N - 1 ) , n ^;

i 1 = 1                   i = k + 1

• -    при нечётных значениях N для гармоники с номером n=N :

  б) Выражения для составляющих дискретного спектра на множестве (54):

  - для постоянной составляющей при нечётных значениях N :

  
  

  S k (0)

  ^A k ,0 t

  
  

  - ( ₁ ) 0.5 ⁽ N ^{+ 1 )} N ( ₁ ) 0.5 ⁽ N ^{- 1 )}

  
  

  π N ²

  
  

  π N

  
  

  ;(58)

  
  

  - для комплексной амплитуды n- ой гармоники

  
  

  A ' k , n

  
  

  _ 2 S k ^{( n} ^ i )

  
  

  T

  
  

  ПП    i т     nn ( N -1 )

  .0.5( N + 1) ■ • Sin -у - N COS 2 N

  22    ;

  n ( N - n )

  
  

  - для гармоники с номером n=N:

  ^A ' k , N = nN .                 ( ⁶⁰ )

  в) Выражения для составляющих суммарного спектра на множестве (54)-(55):

  - для постоянной составляющей для нечётных значений N :

  
  

  A n = 0.            (67)

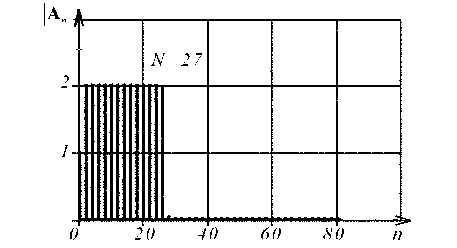
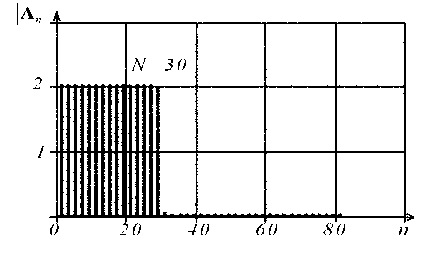
  По графикам полученного амплитудного (рис. 3,а,в) и фазового (рис. 3,б,г, где Ф _п = arg ( A _n ) ) спектров для чётных и нечётных значений N видим:

  • 1)    появление в спектре функции (12) паразитных гармоник;

  • 2)    искажение равномерности основного амплитудного спектра;

  • 3)    фазовый спектр принимает два значения – 0 и 180 градусов, причём в рабочей полосе частот фазовый спектр нулёвой.

  Вклад паразитных гармоник определён выражением для коэффициента гармоник

  
  

  ^k г , N

  
  

  kN ■ N

  0.5 E A n

  n = N + 1

  N

  A ,^{2 +} o.5 E A n

  n = 1

  
  
  
  

  A k ,0 = 2 A ' k ,0   ;

  
  
  
  

• -    для комплексной амплитуды n- й гармоники:

Так как в рабочей области значения амплитудного спектра модели (12) колеблется относительно значения Am=2 – значения

а)

в)

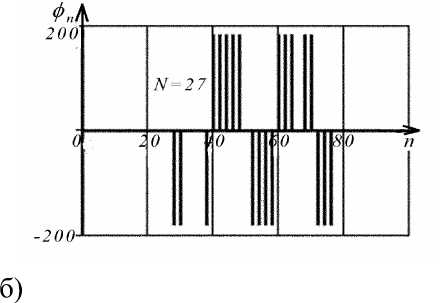
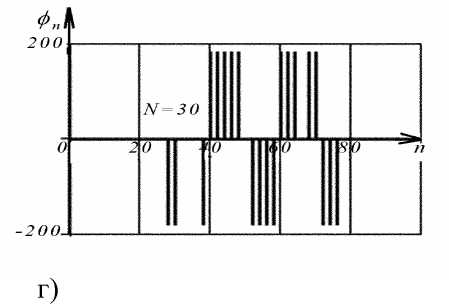
Рис. 3. Графики амплитудного (рис. 3,а,в) и фазового (рис. 3,б,г, где ф_п = arg ( A n ) ) спектров

амплитуд косинусоидального спектра полинома (4), то неравномерность предлагается оценивать с помощью выражения

А

max, N

max ( -^ ■ 100 )

=2,4, _ , N -1 Am           '

max ( A - Am ■ 100 )

;1,3,..., N-1 Am при нечётных N, при чётных N.

Указанные характеристики просчитаны в среде MathCad для N=10,…,200 при l=2, k=3 и для N=6,…,200 при l=1, k=1 . Расчеты показали, что величина коэффициента гармоник паразитного спектра не превышает значения 0.6%, а степень неравномерности -2,2%.