Увеличение зоны просветления оптических деталей большой кривизны

Оптические детали, поверхности которых имеют сферическую форму большой кривизны (полусфера), часто используются как фокусирующие и коллимирующие детали, идеально подходят для применения во многих системах, используемых в волоконной связи, эндоскопии, микроскопии, оптических приёмных устройствах, широкоугольных объективах и лазерных измерительных системах [1, 2]. Для повышения эффективности таких линз на их поверхности обычно наносят просветляющие интерференционные покрытия, основной целью которых является снижение коэффициента отражения от границы раздела двух сред с разными показателями преломления, что позволяет увеличивать пропускание таких элементов [3–6].

Наиболее распространённым методом получения интерференционных слоёв на поверхностях оптических элементов является метод термического испарения плёнкообразующих материалов в вакууме, разновидностями которого являются осаждение материала резистивным или электронно-лучевым способом [7, 8]. При осаждении плёнкообразующих материалов в вакуумной установке на оптическую деталь часто применяют систему двойного вращения оптического элемента. Применение этой системы вращения обеспечивает большую равномерность и симметричность распределения толщины слоя на поверхности детали [9, 10].

В работах [11 – 13] рассмотрены методы получения равномерного распределения относительной толщины слоёв, формирующих покрытие, на сферических поверхностях оптического элемента. Недостатки таких слоёв на сферических поверхностях описаны в работе [14]. В работе [15] описан метод получения слоёв с переменной толщиной при двойном вращении с использованием круглой диафрагмы на сферической поверхности оптических элементов, имеющих большие габариты (радиус больше 50 мм) и малую крутизну, в связи с этим в работе не были рассмотрены экранируемые зоны. Использование наклонного испарителя [16] для формирования слоёв на сферических поверхностях неприменимо, поскольку экранируемые зоны будет асимметричны.

В данной работе рассмотрены анализ траектории движения произвольной точки на сферической поверхности детали большой кривизны, совершающей двойное вращение, и распределение относительной толщины слоя на этой поверхности при формировании его в вакуумной установке. Помимо этого, рассмотрено применение слоя с заданным распределением толщины слоя для увеличения зоны просветления. Зона просветления определяется как отношение радиуса области поверхности оптического элемента, в которой энергетический коэффициент отражения меньше некоторой величины, к его радиусу ( р / R ).

Постановка задачи и ход её решения

При формировании слоёв равномерной толщины, формирующих просветляющие покрытия [17] на сферических поверхностях большой кривизны, размер зоны просветления незначительный, что было показано в работе [14]. Также в работе [14] были рассмотрены интерференционные слои, входящие в состав просветляющих покрытий, геометрическая толщина которых плавно увеличивается вдоль радиальной координаты оптической детали по некому закону от центра к краю. Зона просветления при формировании таких слоёв составляет примерно р / R = 80%, такой размер зоны просветления достаточно велик. Обычно на практике при формировании слоёв, входящих в состав просветляющих покрытий, на сферических поверхностях оптических деталей большой кривизны, совершающих двойное вращение, методом термического испарения плёнкообразующих материалов в вакууме, их толщина уменьшается от центра к краю оптической детали [16]. Получение слоёв, геометрическая толщина которых постепенно увеличивается по поверхности детали, практически невозможно при существующих габаритах вакуумных установок. Уменьшение геометрической толщины слоя от центра к краю оптической детали вызывает существенное увеличение энергетического коэффициента отражения, и при этом размер зоны просветления будет незначительным. Быстрое уменьшение энергетического коэффициента отражения объясняется тем, что при нормальном падении пучка излучения угол падения на краю оптической детали существенно увеличивается (рис. 1), при этом фазовая толщина слоя уменьшается от центра к краю детали, что нарушает условие просветления [18] и энергетический коэффи- циент отражения увеличивается.

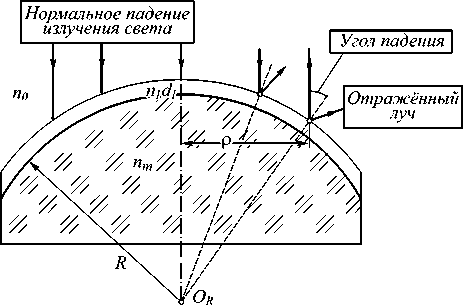
Рис. 1. Изменение угла падения при нормальном падении излучения света на поверхности оптической детали большой кривизны

Для увеличения размера зоны просветления необходимо корректировать уменьшение фазовой толщины слоя в точках, удалённых от центра оптической детали, в области, где коэффициент отражения велик. Для достижения этой цели сначала на поверхность оптической детали наносят слой, выполняющий функцию просветляющего покрытия, то есть его оптическая толщина соответствует условию просветления. Далее в области, в которой коэффициент отражения существенно увеличивается, наносят дополнительный слой из того же материала, но толщина его меняется в зависимости от координаты поверхности оптического элемента. Формирование этого слоя осуществляется при использовании круглой диафрагмы. Такой комбинированный слой, вид которого показан на рис. 2, может существенно увеличить зону просветления. При формировании дополнительного слоя существуют некоторые трудности, которые будут рассмотрены далее.

Рис. 2. Схема комбинированного слоя

Формирование дополнительного переменного слоя

Воспользуемся способом, предложенным в работе [19], для получения дополнительного слоя с заданным распределением толщины на сферических поверхностях.

На рис. 3а показана схема формирования слоя на сферической поверхности. Как показано на схеме, в неподвижной системе координат XYZ сферическая деталь большой кривизны вращается вокруг своей оси O''Z'', удалённой от оси вращения OZ подложко-держателя на расстояние r, и её полюс находится на расстоянии H от плоскости, в которой расположен испаритель, a – расстояние от малого поверхностного испарителя до оси вращения подложкодержателя, θ – угол между линией, соединяющей точку Р на испарителе и исследуемую точку А на поверхности сферической подложки (PA), и нормалью (n) к плоскости, в которой расположен испаритель, θ' – угол между нормалью (n') к сферической поверхности в точке A и направлением (AP) на испаритель, R – радиус сферической детали, ρ0 – габарит сферической детали, ρ – радиальная координата исследуемой точки на поверхности сферической подложки, отсчитываемая по нормали к оси вращения, Нρ – расстояние от плоскости, на которой расположена исследуемая точка с радиальной координатой ρ, до плоскости испарителя. Диафрагма, имеющая радиус rd, удалена от плоскости испарителя на расстояние h и находится в плоскости О'X'Y', параллельной плоскости ОXY, в которой расположен испаритель. Центр диафрагмы Od лежит на оси вращения оптической детали и вращается с угло- вой скоростью ω'.

б)

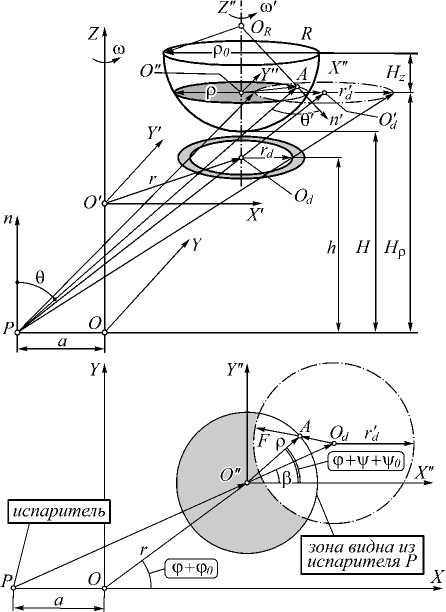
Рис. 3. Схема формирования слоя с заданным распределением через круглую диафрагму на выпуклой сферической поверхности оптической детали, совершающей двойное вращение (а); вид сверху плоскости, на которой расположены исследуемая точка А и проекция окружности диафрагмы в некий момент времени t (б)

Определим распределение толщины слоя как функцию периода обращения Т оптической детали, расположенной на подложкодержателе, вокруг оси вращения OZ . Допустим, что в начальное время ( t = 0, ϕ = 0) в системе координат XYZ положение оси вращения оптической детали имеет некую начальную угловую координату ϕ 0 и исследуемая точка А , расположенная на поверхности детали, имеет начальную координату вращения ψ 0 ( ψ = 0). Через некий момент времени t , если подложкодержатель вращается вокруг свой оси OZ со скоростью ω , положение центра вращения оптической детали O'' в системе координат XYZ определяется угловой координатой ( ϕ + ϕ 0 ), где ϕ = ω t , а оптическая деталь вращается вокруг своей оси О''Z'' со скоростью ω ' , и положение исследуемой точки А в системе координат XYZ определяется угловой координатой ( ϕ + ψ + ψ 0 ), где ψ = ω 't . При равномерном вращении подложкодержателя и подложек ω ' = ωα , тогда величина ψ = ϕα , где α – коэффициент, определяющий отношение углов поворота подложко-держателя и оптической детали. Вследствие этого можно определить координаты точки А в системе координат XYZ таким образом:

-а = r cos(^ + ^o) + p cos(9 + v + Vo), ” Уа = rsin(^ + ^0) + Psin^ + V + Vo), _Za = Hp= H±(R- VR2 -p2).

В этой системе координаты испарителя P и центра O R сферической поверхности могут быть определены следующим образом:

x_P =- а , y_P = 0, zP = 0, x_OR = r cos( ϕ+ ϕ ₀), y_OR = r sin( ϕ+ ϕ ₀), zO_R = H ± R ,

где знак «+» относится к выпуклой, знак «–» – к вогнутой поверхностям.

Если исследуемая точка А полностью видна из испарителя, тогда толщина слоя в зоне исследуемой точки А может быть определена следующим образом [20]:

d =

β mN ^T cos θ cos θ ' d ϕ

π g ⁰      PA ²

где N – количество периодов обращения T , ϕ – угловая координата оси вращения оптической детали, β – коэффициент конденсации, g – плотность образовавшегося слоя, m – масса осаждаемого вещества.

Для того, чтобы определить толщину слоя, необходимо определить cos θ, cos θ ' , расстояние P A между исследуемой точкой A и испарителем P и период обращения Т. Три первых параметра вычисляются таким образом:

PA = Px ² + Py ² + Pz ² ,

Hρ H±(R- R2-ρ2) cosθ= = p       P

PA           PA

cos θ ' =

nP + nP + nP xx yy zz

PA где (nx, ny, nz) – составляющие единичного вектора ORA и (Px, Py, Pz) – составляющие вектора АР, определяющиеся при известных координатах точек A, P и OR, описанных в выражениях (1), (2) и (3) соответ- ственно:

p cos(^+v + Vo)

n- =±-------R• p sin^+v+Vo)

n = ±-------R’

Л^,(

^P- = ^{- (} a ⁺ r ^cos( V ⁺ Ф о ) ⁺ p ^cos( V ⁺ V ⁺ V o )) , Py =- ( r sin( ^ + ^ o ) + p sin( ^ +V +V o )), _ Pz =- ( H ± ( R - 4R ² -p ²)).

Вычисление последнего параметра T вызывает некоторые трудности: во-первых, любая точка на поверхности оптической детали имеет начальную угловую координату ψ0 и движется по своей траектории при двойном вращении детали; во-вторых, скорости вращения оптической детали и подложкодержателя разные, они могут быть кратными или некратными друг другу, то есть коэффициент α может быть целым или дробным числом; в-третьих, использование диафрагмы, которая перекрывает часть потока испаряе- мого вещества, падающего на поверхность детали, приводит к тому, что при движении вокруг оси OZ точка А может быть частично, а не полностью видна из испарителя.

Действительно, при анализе системы уравнений (6) в программе MatLab удаётся моделировать и наглядно рассмотреть траекторию движения точки А, расположенной на поверхности оптической детали, имеющей радиальную координату ρ. На рис. 4а представлена траектория движения некоторых точек радиальной координаты ρ =6 мм на выпуклой сферической поверхности детали, ось вращения которой расположена на расстоянии r =30 мм от оси вращения подложкодержателя. Параметры оптической детали: R = 10 мм, ρ0= 10 мм; вакуумной установки: H =460 мм, а =230 мм. Кривая 1 соответствует точке, начальная угловая координата которой ψ0=0°, кривая 2 – ψ0=90° и кривая 3 – ψ0= 180° соответственно. В данном случае коэффициент α=2, то есть скорость вращения оптической детали вдвое больше скорости вращения подложкодержателя. Как видно из графика, представленного на рис. 4а, при разных начальных угловых координатах ψ0 эти точки движутся по разным траекториям движения, но форма траекторий не меняется, так как отношение углов поворота под-ложкодержателя и оптической детали не меняется. Если меняется значение величины коэффициента а, то форма траектории движения точки меняется (рис. 4б).

га

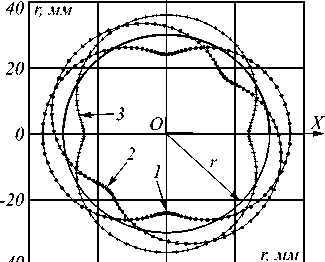
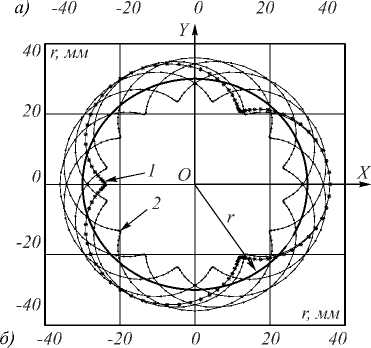
Рис. 4. Вид сверху на траекторию движения некоторых точек, имеющих радиальную координату 6 мм. Параметры оптической детали: R = 10 мм, ρ 0 = 10 мм; ВУ: H = 460 мм, а = 230 мм. Коэффициент a = 2, T=2п, кривые: 1 - у 0 = 0°, 2 - у о = 90°, 3 - у о = 180° (а);

кривые: 1 – коэффициент α = 3, T = 2π;

2 - коэффициент a = 3,2, T= 10 п (б)

Кривая 1 отображает траекторию движения, соответствующую коэффициенту а = 3 , кривая 2 - а = 3,2 соответственно, в данном случае период обращения Т = 2п при коэффициенте а = 3 и Т = 10 п при а = 3,2. В общем случае с помощью программы MatLab и математического анализа период обращения T определяется наименьшим общим кратным двух чисел 2 п / | а | и 2 п /| а -1|, так как величина а может принимать как отрицательные, так и положительные значения. В случае, когда подложкодержатель и оптическая деталь вращаются в противоположные стороны, при определении периода T находится абсолютное значение коэффициента а .

Далее определим для ниже найденного периода T , в каком интервале угловой координаты ф точка А будет видна от испарителя. Для нахождения зоны видимости от испарителя под интеграл вводим функции ограничения, идея которых была рассмотрена в работе [15]. Первая функция соответствует тому, что если исследуемая точка А на поверхности детали находит-

ся внутри окружности, являющейся проекцией окружности круглой диафрагмы, то есть данная точка видна от испарителя (рис. 3 б ), тогда функция принимает значение, равное единице. Вне этой зоны она будет равна нулю. Таким образом, данная функция

определяется так:

F 1 = 2

1 -

AOd ^- rd

AOd

-

H P h

H P h

где АО' d – расстояние от исследуемой точки до центра проекции окружности круглой диафрагмы на плоскости, в которой расположена точка А . АО' d определяется следующим образом:

AOd

= ^p2 +(О Od)

O Od =

H p

- h

h

в = arcsin

- 2 p О Od cos^ + y + y ₀ -P )

^ ( a + r cos( ф+ ф о ))² + ( r sin( ф + Ф 0 ))²

r sin( ф + ф о )

ч Т(а + ГСО8(ф + ф0))2+1^1п(ф + ф0))2

На рис. 5 показаны три зоны, в которых точка А , расположенная на поверхности детали и имеющая радиальную координату p = 6 мм, частично видна из испарителя. Параметры оптической детали и ВУ приведены выше, диафрагма радиусом r d = 5,56 мм расположена на расстоянии h = 443,34 мм от плоскости, в которой расположен испаритель, ось вращения сферической поверхности детали расположена на расстоянии r = 30 мм от оси вращения подложкодержателя, коэффициент а = 2. Кривые: 1 - траектория точки А , 2 – траектория центра проекции окружности диафрагмы, 3 – траектория радиуса r' d проекции окружности диафрагмы; 4 – три зоны, в которых точка А

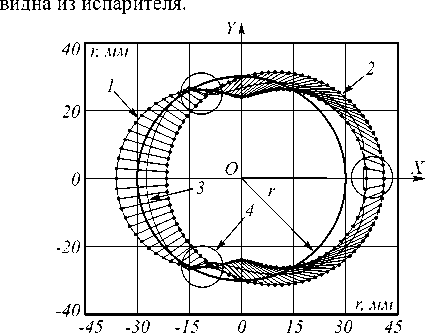
Рис. 5. Зоны, в которых точка А видна из испарителя при её движении вокруг оси вращения подложки через период Т

Вторая функция соответствует моменту касания молекулярного пучка плёнкообразующего материала сферической поверхности. Если угол 6' (рис. 3 а ) превышает п /2, то осаждения слоя не происходит, т.е.

значение этой функции равно нулю, в противоположном случае оно будет равно единице.

F = ¹ | 1 ² 2 1

-

θ ' - 0,5 π

θ ' - 0,5 π

Третья функция определяет возможную зону фор- мирования слоя, т.е. ситуацию, когда осаждение слоя происходит только внутри габаритного радиуса детали. Вне этой зоны осаждения не будет.

F 3 = 2

V

1 +

V R ^{2 -p 2 -} RR ^{2 —p} 0 | R- 2. - , R p | ,

При вычислении толщины слоя для удобства часто используют понятие относительной толщины, под которой понимается отношение толщины слоя в зоне с радиальной координатой ρ к толщине слоя, полученного в центре подложки при отсутствии диафрагмы. Таким образом, относительная толщина может быть определена таким образом [19]:

T FF F cos θ cos θ '

J o ^{1 2 3} „2 ---------d^

d / d ₀ =      _{T    H} ^P ₂           .                (10)

^{J o} ( H ² + a ²)^{2 d}^

Выражение (10) позволяет нам получить распределение дополнительной толщины слоя по поверхности оптической детали большой кривизны, совершающей двойное вращение в вакуумной установке, с целью увеличения зоны просветления.

На рис. 6 а проведено распределение относительной толщины слоя по поверхности детали, сформированного в вакуумной установке с параметрами H , h , r , а , r d , R , ρ 0 , представленными выше, коэффициент α =2, при разных начальных угловых координатах ψ 0 =0°, 90° и 180°.

Как видно из рис. 6 а , при разных начальных угловых координатах ψ 0 распределение относительной толщины слоя в каком-то диапазоне радиальной координаты ρ имеет небольшое отклонение. Это объясняется разными траекториями движения в разных значениях ψ 0 , как показано на рис. 4 а . На рис. 6 б показано распределение относительной толщины слоя в виде 3D-графика. Данное распределение обладает симметричным характером, что является преимуществом при формировании слоя в системе двойного вращения оптической детали по сравнению с формированием при одинарном вращении.

Применение метода формирования переменного слоя для увеличения зоны просветления на сферических поверхностях оптической детали большой кривизны

Выше был рассмотрен метод формирования слоя с заданным распределением толщины в области сферической поверхности большой кривизны, удалённой от центра, в которой энергетический коэффициент от- ражения быстро увеличивается с целью увеличения зоны просветления.

В качестве примера рассмотрим формирование просветляющего однослойного покрытия для увеличения зоны просветления на выпуклой поверхности оптической детали радиусом R = 10 мм и ρ0 = 10 мм, в вакуумной установке с геометрическими параметрами: H =460 мм, а =230 мм, коэффициент α =2. Как было описано выше, сначала формируется слой, показатель преломления которого n1 = 1,35 (MgF2) на поверхности оптической детали, изготовленной из оптического материала с показателем преломления nm = 1,65 (ТФ1), потом на краю оптической детали формируется дополнительный слой с заданным распределением толщины и таким же показателем преломления n1 при использовании круглой диафрагмы с радиусом rd = 5,56 мм, которая расположена на расстоянии h = 443,34 от плоскости, в которой располо-

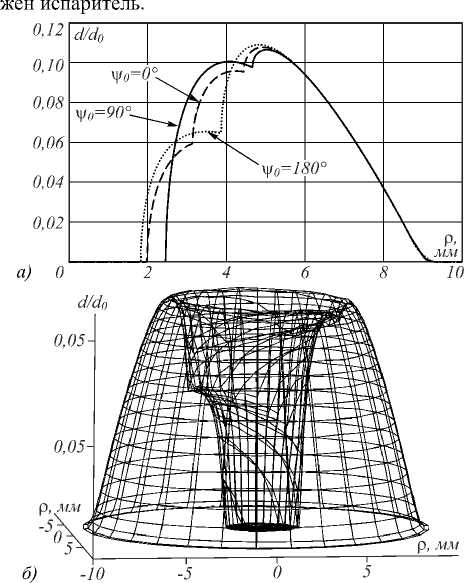
Рис. 6. Распределение относительной толщины слоя на выпуклой поверхности подложки при разных начальных угловых координатах (а); 3D-распределение относительной толщины слоя (б)

На рис. 7 показано распределение геометрической толщины комбинированного слоя просветляющего однослойного покрытия на поверхности оптической детали при разных начальных угловых координатах ψ 0 = 0°, 90° и 180°.

Как показано на рис. 7, в центральной зоне оптической детали формируется слой, оптическая толщина которого удовлетворяет условию просветления для однослойного покрытия, то есть n1d1 = λ0/4, где λ0 =550 нм. На краю оптической детали формируется слой с заданным распределением толщины, который накладывается на ранее полученный слой, толщина последнего определяется количеством N = 200 периодов обращения T = 2π. Распределение энергетического коэффициента отражения по поверхности оптической детали, на которую планируется нанесение вышеописанного покрытия термическим методом в вакуумной промышленной установке типа ВУ-2М, представлено на рис. 8. Очевидно, что зона просветления, в которой энергетический коэффициент отражения меньше 1 %, увеличивается при формировании комбинированного слоя. В данном случае эта зона составляет ρ / R = 65,9%, в случае без применения диафрагмы она составляет примерно ρ / R = 51,5 %, то есть зона просветления увеличивается на 14,4% на

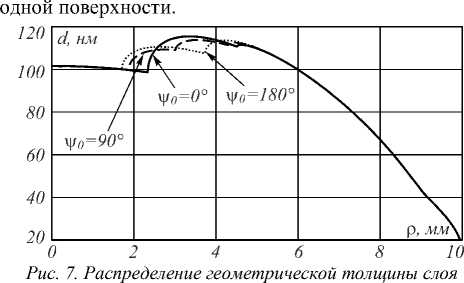
однослойного покрытия на выпуклой сферической поверхности оптической детали

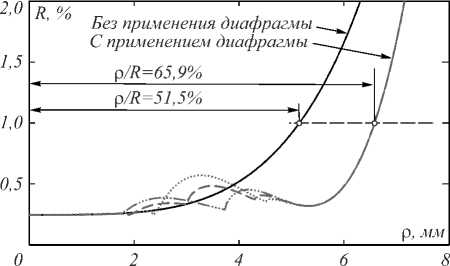
Рис. 8. Распределение энергетического коэффициента отражения по поверхности оптической детали радиусом 10 мм

Заключение

В данной работе представлен разработанный метод увеличения зоны просветления при использовании системы двойного вращения оптической детали большой кривизны в вакуумной установке. Данный метод заключается в том, что на краю сферической поверхности оптической детали, в зоне которого энергетический коэффициент отражения существенно увеличивается, формируется дополнительный слой с заданным распределением толщины с целью корректировки фазовой толщины слоя в этой зоне, что позволяет увеличить зону просветления на сферических поверхностях. Приведено математическое моделирование траектории движения произвольной точки на сферической поверхности оптической детали, которое позволяет определить период обращения подынтегральной функции.

В работе рассмотрено формирование комбинированного однослойного просветляющего покрытия на поверхности оптической детали, изготовленной из оптического материала с показателем преломления n m = 1,65 ( ТФ1 ), и показано, что при формировании данного покрытия можно увеличить зону просветления на 14,4 %.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках госзадания (тема № 3.2506.2017/4.6).