Вариации жесткостей обрезания космических лучей во время сильной геомагнитной бури в ноябре 2004 г

Планетарное распределение жесткости геомагнитного обрезания (ЖГО) космических лучей (КЛ), т. е. самой низкой жесткости, которой должна обладать частица, чтобы проникнуть в заданную точку в магнитосфере, определяется пространственной структурой и интенсивностью магнитосферного магнитного поля. Динамические процессы в магнитосфере приводят к вариациям магнитосферного магнитного поля и, следовательно, к вариациям КЛ, которые связаны с изменениями ЖГО [Dorman et al., 1973; Flueckiger et al., 1986; Smart et al., 2000].

Проблема влияния возмущений геомагнитного поля на ЖГО наиболее детально рассмотрена в работах [Shea et al., 1965, 1976; Dorman et al., 1973; Flueckiger et al., 1983; Тясто, 1991; Smart et al., 2000; Kress et al., 2004; Belov et al., 2005; Tyasto et al., 2008; Kudela et al., 2008].

Для определения ЖГО обычно используется метод прослеживания траекторий частиц КЛ в магнитном поле магнитосферы, описываемой моделью, в которой учитываются магнитное поле внутренних источников и поля от систем электрических токов в магнитосфере.

В большинстве статей рассматриваются изменения ЖГО во время умеренных геомагнитных возмущений. Оценки временных изменений ЖГО и асимптотических направлений для отдельных наземных станций, полученные для разных моделей магнитосферного магнитного поля во время сильных магнитных возмущений, весьма существенно различаются [Kudela et al., 2008]. Сильные магнитные бури являются относительно редкими явлениями, следовательно, данные для очень возмущенных периодов составляют малую часть данных, используемых для создания эмпирических моделей магнитного поля магнитосферы. Это объясняет, почему модели магнитосферного магнитного поля для сильно возмущенной магнитосферы [Tsyganenko, 2002a, b; Tsyganenko et al., 2003; Tsyganenko, Sitnov, 2005] были разработаны позднее, чем модели для умеренных бурь.

Солнечные вспышки и эруптивные выбросы наблюдались в конце октября — начале ноября 2004 г. Повышенная солнечная активность была связана с прохождением по диску Солнца двух групп пятен — активных областей (АО) 10691 и 10696 [Ермолаев и др., 2008]. Число и мощность вспышек были не очень высоки, тем не менее магнитная буря 7–13 ноября 2004 г. была одной из самых сильных за весь период наблюдений D _st-индекса. Буря, по-видимому, была вызвана межпланетным корональным выбросом массы с сильным магнитным полем южного направления (~45 нТл). Эта магнитная буря состояла из двух бурь, следующих одна за другой. Минимум D _st первой бури ( D _st= - 373 нТл) приходится на 06 UT 8 ноября, второй бури ( D _st= - 295 нТл) – на ~10 UT 10 ноября 2004 г. Начальная фаза второй бури наблюдалась на фазе восстановления первой бури, когда D st -вариация была еще достаточно сильной (~100 нТл).

Целью нашей работы является исследование изменений проникновения КЛ во внутреннюю магни- тосферу, вызванных возмущением магнитного поля во время бури 7–14 ноября 2004 г. Мы использовали модель Цыганенко, которая описывает магнитосферное магнитное поле в условиях сильной возмущенно-сти [Tsyganenko, 2002a, b; Tsyganenko et al., 2003]. Для расчета ЖГО методом СГС были взяты данные наблюдений КЛ мировой сети нейтронных мониторов [Dvornikov, Sdobnov, 2002].

1.    МЕТОДЫ

Мы сравнили изменения ЖГО ∆Rэф и ∆RСГС, полученные двумя принципиально разными методами, т. е. методом расчета траекторий частиц КЛ в магнитном поле по модели Цыганенко T03 [Tsyganenko, 2002a,b; Tsyganenko et al., 2003] (∆Rэф) и методом СГС (∆RСГС) по экспериментальным исправленным на давление данным регистрации интенсивности КЛ мировой сетью нейтронных мониторов (38 NM). Первый метод можно назвать теоретическим, второй — экспериментальным. Магнитное поле в модели Цыганенко T03 представляет собой сумму главного магнитного поля от внутренних источников и поля от внешних источников (магнитосферных токовых систем). Главное магнитное поле от внутренних источников представлено международным аналитическим полем (МАП) (International Geomagnetic Reference Field — IGRF) для эпохи 2000 г. и экстраполировано на 2004 г. с учетом вековых вариаций [http// ].

Изменения ∆ R _э ф и ∆ R _сгс определялись для каждого часа в период 7–13 ноября 2004 г. как разности между рассчитанными значениями ЖГО, теоретическими и экспериментальными, и ЖГО в спокойный добуревой период (6 ноября 2004 г.). Расчеты были выполнены для станций КЛ, расположенных на разных широтах и имеющих разные ЖГО для спокойного времени: Хобарт, Рим, Москва, Иркутск, Алматы и Токио. ЖГО в главном геомагнитном поле для этих станций перекрывают большую часть области влияния геомагнитного поля на КЛ. Значения среднесуточных эффективных ЖГО R 0 6 ноября 2004 г. составляли 1.78 ГВ для Хобарта, 2.12 ГВ для Москвы, 3.25 ГВ для Иркутска, 6.09 ГВ для Рима, 6.18 ГВ для Алматы и 11.01 ГВ для Токио.

1.1.    Теоретический метод определения ЖГО (метод расчета траекторий)

Чтобы рассчитать изменения эффективных жесткостей обрезания ∆Rэф теоретически, мы использовали метод прослеживания траекторий частиц КЛ в модельном магнитосферном магнитном поле [McCracken et al., 1962; Дорман и др., 1972; Dorman, 2004, 2009]. Траектории частиц могут быть разрешенными или запрещенными [Дорман и др., 1972; Shea et al., 1976; Cooke et al., 1991; Dorman, 2004, 2009]. Если отрицательно заряженная частица, движущаяся от Земли наружу из данной точки на поверхности Земли в заданном направлении, может достичь границы магнитосферы, то ее траектория считается разрешенной [Cooke et al., 1991]. Такая разрешенная траектория идентична траектории положительно заряженной частицы, приходящей из межпланетного пространства через магнитосферу в заданную точку с того же направления. Траектории считаются запрещенными, если движущаяся наружу отрицательно заряженная частица не достигает границы магнитосферы. Эффективная жесткость обрезания определяется как

R _U

R^ = Ru - Я ARi (разрешенные), i=Rl где траектории рассчитываются с интервалом по жесткости ARi; Rи — верхняя пороговая жесткость, RL — нижняя пороговая жесткость [Cooke et al., 1991]. Верхняя пороговая жесткость RU — максимальная жесткость, при которой наблюдается первый переход от разрешенных траекторий к запрещенным в серии рассчитанных траекторий; нижняя пороговая жесткость RL — жесткость, при которой наблюдается последний переход от разрешенных траекторий к запрещенным. Rэф можно рассматривать как теоретическую жесткость обрезания.

Магнитное поле было представлено эмпирической моделью Цыганенко Т03, описывающей сильно возмущенную конфигурацию магнитосферного магнитного поля и его эволюцию во время бури [Tsyganenko, 2002a, b; Tsyganenko et al., 2003]. В модели полное магнитное поле магнитосферы рассматривается как сумма полей, генерируемых внутренними и внешними источниками; учитываются вклады от таких внешних источников, как симметричный и асимметричный круговые токи, токи на магнитопаузе, биркеландовы токи и токи хвоста магнитосферы. Как указано выше, магнитное поле от внутренних источников было представлено моделью IGRF-2000 (МАП). Входными параметрами модели T03 являются Dst-вариация, компоненты межпланетного магнитного поля (ММП) Bz и By, плотность Nsw, скорость Vsw и динамическое давление Pdyn солнечного ветра [].

1.2.    Метод СГС

Жесткости геомагнитного обрезания A R СГС определялись методом СГС, в котором данные измерений КЛ на мировой сети нейтронных мониторов рассматриваются как единый многоканальный прибор [Dvornikov, Sdobnov, 2002]. С помощью этого метода можно разделить наблюдаемые вариации КЛ на вариации межпланетного и магнитосферного происхождения. Предполагается, что анизотропия функции распределения КЛ вне земной магнитосферы зависит от питч-углов в ММП и от градиента плотности на ларморовском радиусе частицы [Dvornikov, Sdobnov, 2002]. Вариацию интегрального вторичного потока δ I _c/ I c (по отношению к фоновому уровню I c ), наблюдаемую в географическом пункте с жесткостью обрезания R _c на высоте h _c, можно представить как

-^ ( h J = - - R c ( R c ) W ( R _c, h )

1 + J ( R_c )

+

Л/

2 n /2 да от

+ J J J — ( R , T c ( R , a, p ) , Z_c ( R , a, p ) ) x        (1)

00Rc J xWc (R, a, p, h )sinpdRdpda.

Здесь δRc(Rc) — вариация ЖГО Rc,  J (R ) — вариация интенсивности первичных КЛ; Wc(R, α, β, hc) — коэффициенты связи между первичным и вторичным потоками КЛ, которые удовлетворяют условиям нормировки

J d a J" sin p d p J W* ( R _c, a, p, h ) dR = 1, 0       0               R c (a, в)

где α, β — азимутальный и зенитный угол прихода первичных частиц на границу атмосферы; Ψ c ( R , α, β) и λ c ( R , α, β) — асимптотические углы прихода частицы в солнечно-эклиптической системе координат. Первый и второй члены в правой части (1) представляют собой вариации КЛ геомагнитосферной и внемагнитосферной природы. Мы ограничили наше внимание двумя сферическими анизотропными гармониками [Dvornikov, Sdobnov, 2002]. Зависимость δ R _c( R _c) была представлена как

-R(R) = (bR + b2R2)(J-R )/fa1 + ^ + a3- +1).(2) c c   1c  2c    c23

^{x   7} V R RR )

Амплитуды вариаций интенсивности КЛ для пункта с жесткостью R _c можно записать в виде ряда

J (Rc) = ^T a о kR;k..(3)

Jk

Вариации потока первичных КЛ задаются как

J ( R , T , Z) = ]h a 0_t R c^k +

J 2  2 r        k=1       .2

+ZZ[( CnkR- k) Pn (H)]+Я di kR-k) P„ (v), n=1 k=1

где P_n ( p ) и P_n ( v ) — полиномы Лежандра;

p=cos®=smXsmX0+cosXcosX0cos(y-^0X где Θ — угол между вектором скорости частицы V и вектором ММП B (питч-угол); углы у0 и Х0 характеризуют ориентацию поля в геоцентрических эклиптических координатах; углы у и Х определяют направление движения частицы на границе магнитосферы Земли.

Имеем v =cosФ=sin Х sin ^ ₀+cos Х cos ^ ₀cos( ^ -Ф₀), где Ф — угол между V и B V n _±; V n_L — компонента градиента плотности КЛ, перпендикулярная B , углы ^ 0 и Ф₀ характеризуют ориентацию вектора B V n_L . По условию ортогональности векторов B и B V n_L угол ^ 0 может быть представлен как

^ ₀=аrctg[-(cos ^ ₀cosФ₀+sin ^ ₀sinФ₀)cos Х ₀].

Спектры жесткости изотропной и анизотропной компонент апроксимировались рядами по обратным степеням жесткости частиц.

С учетом вышеизложенных предположений интенсивность вторичных КЛ (измеренных на поверхности Земли) описывается следующей системой нелинейных алгебраических уравнений:

5I у (h,) = -ARc W (Rc, h{) + c

* Г 3                2   2                        _

+ f ! l a --':* + EE [ ( h-R - * ) P n ( и ) ]

R I * = 1                 П = 1 * = 1

c

+ Z ( d i* R  ) P ( v ) Г W c ( R , ^а’в’ h ) dR .

к = 1                         J

5 Ii    .

Здесь —-(h) — амплитуды вариаций интегрально-Ic го потока вторичных частиц (относительно некоторого фонового уровня I i ), наблюдаемых в геогра- фическом пункте с жесткостью Rс на высоте h в атмосфере Земли (т. е. данные нейтронных мониторов мировой сети). В уравнениях (2)–(5) асимптотические углы Yc(R) и Хс(R) прихода частиц в пункт c жесткостью Rс, должны использоваться вместо у и X.

Неизвестные параметры b 1 , b 2 , a 1 , a 2 и a 3 описывают вариации ЖГО R _c; a ₀₁, a ₀₂, и a ₀₃ — вариации дифференциального спектра жесткости изотопной компоненты; c ₁₁, c ₁₂, c ₂₁, c ₂₂, d ₁₁ и d ₁₂ связаны с двумя компонентами первой и второй гармоник углового распределения КЛ; ^ о , X ₀, с ₀ и Ф_о определяют ориентацию осей симметрии. Эти неизвестные параметры были рассчитаны методом наименьших квадратов [Dvornikov, Sdobnov, 2002; Dorman, 2009]. Таким образом, метод СГС позволяет определить изменения ЖГО, вариации параметров спектра жесткости КЛ и анизотропию в межпланетном пространстве. В этой работе мы ограничились исследованием только ЖГО, полученных этим методом в широкой области широт. Изменения в ЖГО Δ R СГС , полученные методом СГС, можно считать экспериментальными.

2.  РЕЗУЛЬТАТЫИ ОБСУЖДЕНИЕ 2.1.    Временные вариации жесткости геомагнитного обрезания в период бури 7– 13 ноября 2004 г.

Временные изменения в рассчитанных A R эф

(кружки) и экспериментальных ARСГС (крестики) ЖГО 7–13 ноября 2004 г. показаны на рис. 1 для станций Токио, Алматы, Рим, Иркутск, Москва и Хобарт. В нижней части показаны Dst-индекс, Kp-индекс, скорость Vsw и плотность Nsw солнечного ветра [ ]. Видно, что максимальное понижение ЖГО наблюдается 8 и 10 ноября 2004 г. в периоды главной фазы первой (7–10 ноября 2004 г.) и второй (9–11 ноября 2004 г.) магнитных бурь. Наиболее сильные понижения ARэф, до 1.5 ГВ, наблюдаются

8 ноября на всех станциях. В связи с этим следует обратить внимание на анализ вариаций ЖГО во время сильного геомагнитного возмущения в октябре–ноябре 2003 и ноябре 2004 г., проведенный в работах [Kuznetsov et al. 2006] и [Kudela et al. 2008]. Для расчетов A R _э ф авторы использовали магнитосферную модель Цыганенко 2004 г. Ts04 [Tsyganenko, Sitnov, 2005], которая является, по их мнению, улучшенной версией модели Цыганенко T03 [Tsyganenko, 2002a, b; Tsyganenko et al. 2003]. Кузнецов и др. [Kuznetsov et al. 2006] получили понижение A R _э ф ~1.15 ГВ на средних широтах для бури в ноябре 2004 г., что довольно хорошо согласуется с нашими результатами.

На рис. 1 видно дополнительное очень сильное понижение экспериментальных ЖГО A R _СГС на ст. Токио 9 ноября 2004 г. с минимальным значением жесткости в 21 UT ( A R _СГС=1.1 ГВ). Это понижение требует дальнейшего исследования.

В целом кривые A R _СГС и A R _э ф лучше коррелируют между собой и с D st -вариацией в период первой бури, чем второй. Наиболее значительные отличия между кривыми A R _э ф и A R _СГС наблюдаются на ст. Москва ( R ₀=2.12 ГВ) и Хобарт ( R ₀=1.78 ГВ) во время минимумов D _st, т. е. в 5–6 UT 8 ноября и в 9–10 UT 10 ноября 2004 г., причем разница между A R _э ф и A R _СГС для ст. Хобарт больше, чем для ст. Москва. Различия между A R _э ф и A R _СГС, возможно, указывают на несовершенство модели на высоких широтах. Действительно, модель T03 описывает магнитное поле возмущенной магнитосферы до расстояний R < 15 R E , при этом поле от токов удаленного хвоста не принимается во внимание. Поперечные токи хвоста в ближней части магнитосферы и токи удаленного хвоста изменяются различным образом. В то время как внутренняя часть токов хвоста очень чувствительна к южной компоненте ММП B z , ток дальнего хвоста отзывается в основном на давление солнечного ветра [Tsyganenko, 2002a, b; Tsyganenko et al., 2003]. Это важно для частиц КЛ с жесткостями R < 5 ГВ, которые приходят к земной поверхности в основном через хвост магнитосферы [Dorman et. al., 1971; Dorman, 2009]. Как показано выше, ЖГО в спокойный день 6 ноября составляла R ₀=2.12 ГВ для Москвы и 1.78 ГВ для ст. Хобарт.

Исследования токовых систем хвоста магнитосферы [Greenspan, Hamilton, 2000; Maltsev, 2004; Maltsev, Ostapenko, 2004] показали, что токи, ответственные за депрессию магнитного поля, имеют большую долготную асимметрию. Они создают аксиально-асимметричное возмущение в магнитном поле магнитосферы, которое может влиять на глобальное распределение ЖГО сложным образом. Результатом этого является то, что ЖГО в некоторых географических пунктах, особенно в районах сильных градиентов и аномалий, могут вести себя нестандартным образом. Например, Пчелкин и др. [Pchelkin et al. 2007] обнаружили, что во время геомагнитной бури в ноябре 2003 г. в районе ст. Мехико наблюдается локальная особенность в мировом распределении ЖГО. Как уже упоминалось выше, на рис. 1 видно довольно сильное понижение экспериментальных ЖГО

. .:    A R (ГВ)                                          а 0.4 0.2 0 - 0.2 - 0.4 - 0.6 - 0.8 - 1 - 1.2 - 1.4 - 1.6 0 .6^ A R (ГВ) 0.4 0.2 0 - 0.2 - 0.4 - 0.6 - 0.8 - 1 - 1.2 - 1.4 - 1.6                                                           в 0.6    A R (ГВ) 0.4 0.2 0 - 0.2 - 0.4 - 0.6 - 0.8 - 1 - 1.2 - 1.4 - 1.6 . .:    A R (ГВ)                                          г 0.4 0.2 0 - 0.2 - 0.4 - 0.6 - 0.8 - 1 - 1.2 - 1.4 - 1.6 0.6    A R (ГВ)                                    Я 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 -1.2 -1.4 -1.6 0.6    A R (ГВ)                                       е                                         v 0.4 0.2 0 - 0.2 - 0.4 - 0.6 - 0.8 - 1 - 1.2 - 1.4 - 1.6 10—1 KpO                                                                       Dst (нТл)® 80 6                                                                                                                                           -100 4                                                                                                                                           -200 2                                                                                                                                           -300 0                                                                                                                                           -400 900    V (км/ср                                                                            N (см - 3) •   80 800 700                                                                                                                               60 600                                                                                                                              40 500 400                                                                                                                               20 300                                                                                                                              0 6  12  18       6  12  18      6  12  18       6  12  18      6  12  18      6  12  18       6  12  18 0      7      0      8      0      9      0      10     0      11     0      12     0      13     ч Д а Н с И ы

Рис. 1. Жесткости обрезания космических лучей в период бури 7–13.11.2004 ( R _э ф — кружки, R _СГС — крестики); а — Токио, б — Алматы, в — Рим, г — Иркутск, д — Москва, е — Хобарт

∆RСГС на низкоширотных станциях. Например, на  может иметь немагнитосферное происхождение ст. Токио наблюдается понижение геомагнитного   [Dorman, 2009].

порога 9 ноября 2004 г. с минимумом ∆ R СГС =1.1 ГВ в     ^{Результаты анализа ко}рр^{еляций между измене-}

21 UT. Понижение ∆RСГС в это же время наблюдается  ниями ∆Rэф, рассчитанными с использованием модели и на ст. Алматы и Рим, но оно имеет заметно мень-   T03, и экспериментальными ∆RСГС приведены в шую амплитуду и становится меньше с увеличением  табл. 1 и на рис. 2. Корреляционные коэффициенты широты станции. Обычно полагают, что магнито-  K между ∆RСГС и ∆Rэф находятся в пределах 0.76– сферный эффект сильнее на средних широтах и сла-   0.88 на всех станциях, кроме Токио, где коэффи- бее на низких, поэтому можно предположить, что он  циент опускается до 0.27.

0,4

0,4

0,2 -

0 -

-0,2 -

о -0,4 -e1 -0,6 -% -0,8 -

-1 -

-1,2 -

-1,4 -

-1,6 4

-1,5

0,4

0,2 -

0 -

-0,2 -

-0,4 -

^4 -0,6"

0C -0,8 -

-1 -

-1,2 -

-1,4 -

-1,6 4

-1,5

y = 0,2294x - 0,097

0,2 -

0 -

-0,2 -

-1

-0,5

0,5

∆R СГС _Tok

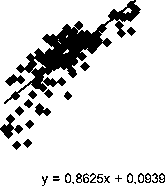
-1

-0,5

0,5

∆ R СГС _Rome

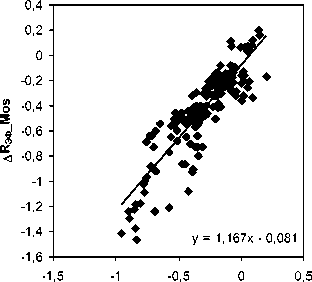
∆R СГС _Mos

Рис. 2 . Корреляция между ∆ R эф и ∆ R СГС для бури 7–13 ноября 2004 г.

Е

e

ОС

-0,4 -

-0,6 -

-0,8 -

-1 -

-1,2 -

-1,4 -

-1,6 4

-1,5

0,4

0,2 -0 -

-0,2 -

5 -0,4 -

-0,6 -

< -0,8 -

-1 -

-1,2 -

-1,4 -

-1,6 4

-1,5

y = 0,7854x + 0,0828

-1

-0,5

0,5

∆R СГС _Alm

♦V y = 0,9278x - 0,0148

-1

-0,5

0,5

∆R СГС _Irk

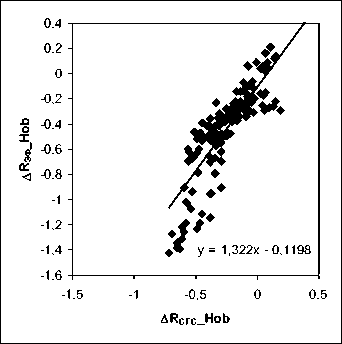
Таблица 1

Коэффициенты K корреляции между ∆ R _СГС и ∆ R _э ф

Станция	Токио	Алматы	Рим	Иркутск	Москва	Хобарт
K	0.27	0.76	0.82	0.87	0.88	0.83

Более детальный анализ коэффициентов K корреляции для Токио, проведенный отдельно для двухглавных фаз первой и второй бурь, показал, что эти коэффициенты сильно различаются: для первой бури K =0.76, для второй K =0.05.

Очень низкая корреляция между теоретическими и экспериментальными значениями ∆ R может быть следствием сильного понижения ∆ R СГС 9 ноября 2004 г. после 14 UT и отсутствия этой особенности в ∆ R эф . Это понижение наблюдается на всех станциях, но понижение в ∆ R эф и соответственно разница между

∆ R _э ф и ∆ R _СГС наиболее заметны на ст. Токио. Заслуживает внимания тот факт, что сильное понижение в ∆ R _СГС 9 ноября в 21 UT на низкоширотных станциях совпадает по времени с приходом межпланетной ударной волны и прохождением переднего края магнитного облака через орбиту Земли [Ермолаев и др., 2005; Ermolaev et al., 2008]. Можно предположить, что подобные эффекты недостаточно полно учтены в модели Цыганенко T03.

В табл. 2 представлены понижения геомагнитных порогов в минимуме D _st-вариаций в ходе первой и второй геомагнитных бурь исследуемого возмущения 7–13 ноября 2004 г.

Видно, что наиболее сильное понижение ∆ R эф ∼ ∼ (68–79) % наблюдалось на ст. Москва и Хобарт во время первой бури и чуть ниже ∼ (56–67) % — во время

Таблица 2

Понижения жесткостей обрезания КЛ во время минимумов D _st

Станция 8 ноября 2004 г. (Dst= -373 нТл) 10 ноября 2004 г. (Dst= -295 нТл) ΔRэф ΔRсгс ΔRэф ΔRсгс ГВ % ГВ % ГВ % ГВ % 1 Токио 0.76 6.9 0.55 5 0.58 5.3 0.42 3.8 2 Алматы 1.04 16.8 0.86 13.9 0.79 12.8 0.8 12.9 3 Рим 1.04 16.4 0.88 14.4 0.91 14.9 0.84 13.8 4 Иркутск 1.36 42.2 1.02 31.4 1.1 33.8 1.02 31.4 5 Москва 1.44 67.9 0.89 42 1.18 55.7 0.82 38.7 6 Хобарт 1.4 78.6 0.68 38.2 1.2 67.4 0.6 33.7 второй. Понижения экспериментальных ∆RСГС для тех же станций несколько ниже — (38–42) % и (34– 39) % соответственно. Таким образом, теоретическое значение ЖГО на ст. Москва в минимуме Dst 8 ноября 2004 г. близко к значению ЖГО для спокойного времени приполярной ст. Апатиты (0.7 ГВ).

2.2.    Корреляции между ∆Rэф и ∆RСГС и межпланетными параметрами

На рис. 3, 4 показаны коэффициенты K корреляции между ∆ R эф и ∆ R СГС с D st -вариацией и межпланетными параметрами — компонентами ММП B_z и B y и параметрами солнечного ветра — плотностью N _sw, скоростью V _sw и динамическим давлением P _dyn. Межпланетные параметры B z , B y , N sw , V sw и P dyn являются входными для модели T03 и определяют структуру и интенсивность магнитного поля во всей магнитосфере. Как видно из рис. 3, 4, коэффициенты корреляции ∆ R эф и ∆ R СГС с D st довольно высоки для всех станций (0.59–0.68), кроме Токио (0.35). D _st-вариация и южная компонента ММП B_z ответственны за ослабление магнитосферного магнитного поля в околоземном космическом пространстве. Мы видим, что корреляция между теоретическими ∆ R эф и B_z довольно высока (0.59–0.68), в то время как корреляция между ∆ R СГС и B z хуже: она составляет всего 0.08 в Токио и 0.33–0.41 для всех других станций. Анализ корреляций между динамическими параметрами солнечного ветра V _sw, N _sw, P _dyn и ЖГО дает несколько неожиданные результаты. Динамическое давление солнечного ветра P _dyn в основном определяется V sw и N sw . Форма и размер магнитопаузы однозначно определены в модели T03 динамическим давлением, ММП и углом наклона геодиполя [Tsyganenko, 2002a, b]. Следовательно, P dyn должно отражаться в ЖГО. Как видно из рис. 3, 4, существует довольно высокая корреляция между V sw и ∆ R _э ф (0.64–0.73) и ∆ R _СГС (0.69–0.73) для всех станций и заметно ниже корреляция для «Токио» (0.40). Корреляция между N _sw и ∆ R _э ф (0.38–0.41), а также между N sw и ∆ R СГС (0.38–0.52) ниже, но все еще значительна. Тем не менее коэффициенты корреляции ∆ R эф и ∆ R СГС с P dyn не выше 0.2.

Возможно, отсутствие корреляции между ЖГО и P _dyn находится в соответствии с результатами статистического анализа экспериментальных данных о параметрах потока солнечного ветра [Khabarova, Rudenchik, 2003], которые показали, что более сильное влияние на P _dyn имеет плотность солнечного ветра,

Коэффициенты корреляции между ∆ R_э ф и Dst и межпланетными параметрами

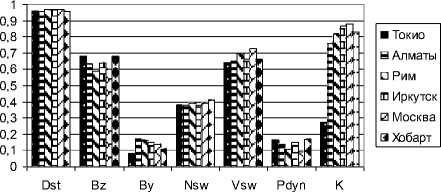
Рис. 3. Коэффициенты корреляции между ∆ R _э ф и D _st и межпланетными параметрами

Коэффициенты корреляции между ∆ R_сгс и Dst и межпланетными параметрами

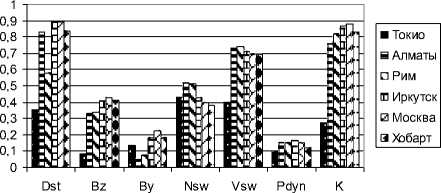
Рис. 4. Коэффициенты корреляции между ∆Rсгс и Dst и межпланетными параметрами а не скорость. Оказалось, что коэффициент корреляции между Pdyn и Nsw составляет 0.77, а коэффициент корреляции между Pdyn и Vsw — всего 0.06. Однако по нашим данным изменения ЖГО коррелируют с Vsw гораздо лучше, чем с Nsw (см. рис. 3).

Таким образом, наши результаты показывают, что именно D _st-вариация имела наиболее выраженный эффект в изменениях ЖГО во время магнитной бури в ноябре 2004 г.

3.    ВЫВОДЫ И ЗАКЛЮЧЕНИЕ

Мы исследовали ЖГО КЛ во время сильно возмущенного периода 7–13 ноября 2004 г. Рассчитывались теоретические эффективные ЖГО методом прослеживания траекторий частиц КЛ в модельном магнитном поле возмущенной магнитосферы (Цыганенко T03). Расчеты были выполнены для ряда станций КЛ, геомагнитные пороги которых в спокойное время охватывают область от ~1.5 до ~11.0 ГВ, т. е. основную область влияния магнитного поля магнитосферы на КЛ. Экспериментальные ЖГО рассчитывались методом СГС по данным регистрации КЛ на мировой сети нейтронных мониторов. Результаты можно резюмировать следующим образом.

• 1.    Было обнаружено, что понижения ЖГО КЛ, полученные принципиально разными методами (методом расчета траекторий частиц в модельном магнитном поле и методом СГС по данным непосредственной регистрации КЛ мировой сетью станций), достигают ~1–1.5 ГВ во время сильной магнитной бури в ноябре 2004 г.

• 2.    Сравнение временных вариаций в экспериментальных ∆ R _СГС и теоретических ∆ R _э ф ЖГО во время рассматриваемого возмущенного периода показало, что оба метода дают похожие результаты. Достаточно высокие коэффициенты корреляции (0.76–0.88) между экспериментальными ∆ R _СГС и теоретическими ∆ R эф для всех станций, за исключением Токио, свидетельствуют о том, что модель T03 отражает основные черты сильно возмущенной реальной магнитосферы. В экспериментальных ∆ R СГС наблюдается аномальное поведение на низкоширотной ст. Токио и в меньшей степени на ст. Алматы и Рим во время второй бури возмущенного периода 7–13 ноября 2004 г. Сильное понижение на 1.1 ГВ в экспериментальных ∆ R _СГС 9 ноября 2004 г. в Токио вызвано эффектом, природа которого пока не известна.

• 3.    Анализ корреляций вариаций ЖГО с D _st и параметрами солнечного ветра показал, что самые высокие коэффициенты корреляции наблюдаются для D st (соответственно 0.85 и 0.95 для ∆ R СГС и ∆ R эф ). Весьма заметные, но гораздо более слабые корреляции отмечаются между теоретическими и экспериментальными ЖГО и N _sw, V _sw, и B_z . Коэффициенты корреляции ∆ R СГС и ∆ R эф с P dyn и B y незначительны (не более 0.2). Таким образом, вариации ЖГО во время рассматриваемого буревого периода в основном обусловлены D _st-вариацией.

• 4.    Результаты, представленные в этой работе, показывают, что изменения теоретических ∆ R _э ф и экспериментальных ∆ R _СГС согласуются между собой. Точность полученных теоретических ∆ R эф определяется точностью модели магнитосферы, построенной по данным спутниковых измерений магнитного поля. В основе точности ∆ R _СГС лежит точность измерений интенсивности КЛ на мировой сети станций.

Таким образом, эмпирическая модель магнитосферы T03, достаточно хорошо описывающая возмущенное магнитное поле, и метод СГС, в котором используется современная сеть станций КЛ, позволяют получать общее распределение изменений ЖГО и их временную динамику.

Эта работа была поддержана РФФИ, грант № 0702-00920 и Программой Президиума РАН № 16. Мы благодарим сотрудников мировой сети станций КЛ.