Вариационная формулировка математических моделей сред с микроструктурами

Models of the continued media with a microstructure are investigated. The media microstructures are defined by the model kinematics of various complexity. The corrected mathematical models are proposed, which include the constitutive equations, governing equations and boundary conditions. Kinematic variational principle is used for formulation of models. The functional of the energy is found using kinematic connections in framework of this variational a principle. Thus, the spectrum of internal interactions is completely determined by system of the kinematic connections realized in the media. The general variant of the theory of media with kept dislocations is elaborated. This theory generalizes known models of the media with microstructures studied by Mindlin, Tupin, Cosserat’s and so on. Some particular models of the media representing interest from the applications point are considered.

В работе развивается алгоритм построения моделей сред с обобщенной кинематикой, который позволяет получать корректную и согласованную математическую формулировку моделей сред с микроструктурами. Приводятся математические модели континуальных сред с обобщенной кинематикой, учитывающие масштабные эффекты.

Для построения математических моделей используется вариационный подход. Вариационные методы являются весьма эффективным инструментом моделирования сред различной сложности, позволяя получать энергетически согласованные математические модели для сред различной сложности. Так, в соответствии с вариационным методом Л.И. Седова [1] определение списка обобщенных переменных (что эквивалентно определению кинематической модели) и вида объемной плотности Лагранжиана позволяет получить определяющие соотношения модели и систему уравнений равновесия (движения), записанную в кинематических переменных. В данной работе используется "кинематический" вариационный принцип, сформулированный в [2]–[5] и развитый в работах [6]–[8]. В соответствии с этим принципом общий вид функционала энергии для исследуемой среды находится по заданным кинематическим связям. Спектр внутренних взаимодействий полностью определяется системой кинематических связей, реализующихся в среде.

Особое внимание будет уделяться общему варианту теории сред с сохраняющимися дислокациями, который обобщает известные модели Миндлина [9,10], Тупина [11], Коссера [12] и Аэро – Кувшинского [13]. Приводится описание актуальных с прикладной точки зрения частных вариантов теории: сред Коссера и Аэро – Кувшинского, пористых сред, сред с «двойникованием». Устанавливается система определяющих соотношений и формулируется согласованная постановка краевой задачи. Эти модели позволяют моделировать масштабные эффекты, связанные с когезионными и адгезионными взаимодействиями.

На первом этапе исследуются кинематические соотношения модели среды, которые позволяют сформулировать кинематические связи для исследуемой среды. В дальнейшем эти связи учитываются в рамках принципа возможных перемещений. На втором этапе устанавливается список аргументов потенциальной энергии деформации (для обратимых процессов) и функционала Лагранжа. Приводится общий вид определяющих уравнений, соответствующих общей форме потенциальной энергии, проводится их анализ, позволяющий ввести некоторые упрощения, связанные с учетом известных экспериментальных данных. В результате дается полная вариационная формулировка математической модели.

Кинематические модели сред

Используется прием, в соответствии с которым исследование кинематики основано на анализе соответствующих соотношений интегрируемости (для бездефектных сред) и неинтегрируемости (для сред с полями дефектов)[14]. Рассмотрим сначала бездефектные среды с непрерывным и дифференцируемым вектором перемещений R i . Запишем расширенные соотношения Коши для компонентов тензора дисторсии d ij . Они являются кинематическими связями между двенадцатью зависимыми степенями свободы Y ij , 0 , to k и R i , которыми наделен произвольно выбранный бесконечно малый параллелепипед:

R i , j = d j =Y j + (1/3) 05 j -to k Э^ . (1)

Здесь, как обычно, по повторяющимся индексам осуществляется свертка, Y j — компоненты тензора девиатора деформаций, 0 - объемная деформация, to _k -псевдовектор поворотов или упругих вращений, Э_]к - компоненты псевдотензора Леви-Чивиты.

Записанные несимметричные соотношения Коши можно трактовать как условие существования векторного потенциала для тензора дисторсии d ij . Очевидно, что условие существования такого потенциала записывается в виде

d in , т Э пт]   ⁰ ■

Среды, в которых имеется непрерывный векторный потенциал тензора дисторсии (вектор перемещений), назовем бездефектными средами Папковича. Соотношения (2) являются условия интегрируемости соотношений (1) (условия интегрируемости перемещений) и называются соотношениями Папковича. Эти соотношения можно переписать в виде toi,j=Yej,а Эaei+ (1/3)0,а Эа]                             (3)

Аналогичным образом запишем условия интегрируемости соотношений (3) (условия интегрируемости вектора поворотов),

( У₆ „ + 3 95₆ „ ), ,. Э„ Д „ = 0.                      (4)

Соотношения (4), обеспечивающие непрерывность упругих поворотов, являются уравнениями совместности Сен-Венана. Уравнения неразрывности (4) можно разрешить относительно производных от объемной деформации в явной форме, выразив их через компоненты тензора-девиатора деформаций:

(1/3) 0 , j = [(1/2^ 5 j +Y т _ц Э а mi Э в _№ Кв .                 (5)

Такая форма уравнений совместности позволяет, с учетом (1),(3), получить формальные точные квадратуры для вектора перемещений, объемной деформации и вектора поворотов только через компоненты тензора-девиатора деформаций [4]. Необходимыми и достаточными условиями (для односвязных сред) интегрируемости системы (5)

являются новые уравнения совместности третьего порядка, записанные относительно только компонент тензора-девиатора деформаций [4]:

[(l/2) ^Y ae 8 ip +^Y m _ц Э a mi Э в _ц p ^] , ав q Э pqj = °.

Рассмотрим дефектную среду с полем дефектов - дислокациями. Если дисторсия d j не имеет непрерывного векторного потенциала, условия интегрируемости перемещений не выполняются. Тогда соотношения Папковича являются неоднородными:

d. , Э -Гу. +1/3)6 5. -окЭ.Д Э . =В...               (6)

in ’ m nmj LI in              in_m ^к^тк J’ m nmj ij ’                            v 7

Если s - + 0 - дисторсия не интегрируема, вектор перемещений как потенциал дисторсии разрыва. Непрерывный тензор «несовместностей» S j перемещений является псевдотензором плотности дислокаций [15] и подчиняется дифференциальному закону сохранения: s j , j = 0. В последнем нетрудно убедиться непосредственно, если учесть несимметричность тензора Э_nm j по индескам m , j . Решение неоднородных уравнений Папковича (6) представляется в виде суммы решения однородного уравнения Папковича d j и частного решения неоднородных уравнений Папковича d j : d j = d ij + d j . Общее решение неоднородного уравнения Папковича (6) можно записать в симметрированном виде:

dj = dj + dj = Yij + (1/ 3)65y -toкЭУк, 6 = 6° + 6S = Rk,к +6S, toк = tok + toS=-(1/2)Ri ’ j Эук +Юк ,                         (7)

Y ij = Y ° +Y S = (1/ 2)( R i , j + R j , i ) - (1/ 3) R k , к 5 j +y f .

Очевидно, что здесь в качестве независимых «обобщенных перемещений» наряду с d j можно рассматривать также следующие величины: y S , ^ю S ,    6^s

( d j =y S + (1/3) 6^S5 _in -to S Э_1пК )• Эти «обобщенные перемещения», связаны со своей «обобщенной деформацией» - тензором «несовместностей» s - (аналог соотношний Коши):

Ξ    Ξ   ΞΞ in, m nmj LI in V *vv xnm хл^ш^ j, m nmj ij .                          V 7

Пользуясь терминологией среды Коссера, to k =- (1/2) R_i , j Э_ijk называют стесненным вращением, а to S - свободным вращением или спином. Аналогично будем называть y ° , и 6 ° - стесненными деформациями, а y S , и 6^s - свободным деформациями.

Среду с тензором дисторсии d j , d j + 0 , удовлетворяющим равенству (6), назовем дефектной средой Папковича - Коссера. Подчеркнем, что в бездефектной, однородной среде Папковича тензор дисторсии является интегрируемым (он удовлетворяет условиям интегрируемости (2)), а непрерывный вектор перемещений может быть определен из несимметричных соотношений Коши путем интегрирования в квадратурах (формулы Чезаро). Введем вектор Бюргерса [15],[16]:

b_i = ∫ d_i ^Ξ _jdx_j = ∫ d_i ^Ξ _js_jds = ∫ d_i ^Ξ _jv_mn_nЭ_jmnds = ^Ξ

J J ij ’ m n jmn J J in n            n J J ^{m .}

где Sj - единичный вектор, касательный к плоскому контуру, nn - вектор единичной нормали к плоскости траектории, а вектора Sj, vm, nn образуют тройку ортов, связан ных с текущей точкой контура. Традиционное разложение дислокаций [16] включает два типа дислокаций (винтовая и краевая): bivi = vi J df“syls, bi ni = ni J df“sjds и bi si = si J djsyls. Такая классификация не отражает энергетической независимости выделенных типов дислокаций. Можно предложить иную классификацию дислокаций, определив следующие три типа дислокаций (bi ) Y, (bi) 0 и (bi) ю :

Mx        1           _              Mx             1 Mx bi = J (Y“ + т0S5ij - ю“ЭУк)dyj = (J Y“dy,) +(. J 0“dyi) +(- J ю“ЭykdУj) =

M 0        3                         M 0            3 M 0

= ( b.) y + ( b) 0 + ( b) ™ .

Mx1

Назовем ( b i ) _Y = ( J y “ dy ) — Y -дислокациями, ( b i ) ₀ = (- J 0 “ dy i ) - 0 -дислокациями и

M0

M x

( b i ) _ю = ( — J ю “ Э i _jkdy_j ) - ^ю -дислокациями. Показано[16], что потенциальная энергия

M 0

свободного формоизменения, пропорциональная величине ~ y “ Y “ , потенциальная энергия изменения объёма ~ 0 “ 0 “ и кручения ~ ю “ ю “ не имеют перекрестных членов. Поэтому потенциальные энергии введенных определений дислокаций аддитивны и могут существовать изолированно и независимо от других типов дислокаций. Предложенная классификация отражает, таким образом, энергетическую независимость выделенных типов дислокаций. Эта классификация дает новую как физическую, так и кинематическую трактовку дислокаций, так как отражает связь дислокаций с формоизменением - y , с изменением объема 0 (пористость) и со скручиванием ю (вихри или спины). Предложенная классификация, фактически позволяет прогнозировать частные случаи сред с сохраняющимися дислокациями, когда в среде доминируют лишь один или два типа дислокаций.

Аналогично можно продолжить построение кинематических соотношений для сред с более общей кинематикой. Рассмотрим тензор дисторсии d ij и тензор кривизн D ijn , который является градиентом тензора дисторсии

D ijn = d ij , n •

Следуя общему алгоритму, рассмотрим условия интегрируемости тензора дисторсии в записанном соотношении

D ijn , m ^d m. = 0.                                          (9)

Условия (9) являются условиями существования криволинейного интеграла при определении тензора дисторсии d in через тензор кривизн D ijn . Назовем их обобщенными соотношениями Сен-Венана.

Иначе говоря, условия интегрируемости (9) являются критерием существования тензорного потенциала для тензора кривизн. Этим потенциалом является тензор дис- торсии – dij . Имеет место полная аналогия со скалярным потенциалом для вектора Ri (среды Коши) и векторным потенциалом для тензора дисторсии (среды Папковича).

Уравнение (9) является обобщением известных уравнений совместности Сен-Венана. Чтобы доказать это, достаточно выделить в тензорном уравнении (9) антисимметричную по индексам i , j часть. В этом частном случае уравнение (9) можно переписать в виде

( - 1/2)( D pqn Э pqs ), m Э nmk = 0.

Это уравнение есть условие существования векторного потенциала ω _i для кривизн (( - 1/2) D_pqn Э_pqs ) = ω _s , _n . С другой стороны, именно уравнения Сен-Венана и являются условиями интегрируемости вектора поворотов. Среды, для которых имеется непрерывный тензорный потенциал у тензора кривизн, будем называть средами Сен-Венана. В «бездефектных» средах Сен-Венана тензор дисторсии d_ij может быть однозначно определен по D_ijn , ибо условия интегруемости (9) для D_ijn выполняются.

По аналогии с предыдущим можно рассмотреть дефектные среды Сен-Венана. Предположим, что в общем случае условия интегрируемости (9) не выполняются, и тогда имеет место неоднородное уравнение

D , Э =Ω ≠ 0. ijn ^, m nmk ijk ^.

Определим интегрируемую и неинтегрируемую части кинематической переменной третьего ранга (кривизны) как соответствующее общее решение однородного уравнения (9) и частное решение неоднородного уравнения (10). Равенство (10) является условием существования полей дефектов более сложного вида, чем дислокаций – обобщенных дисклинаций. Псевдотензор–источник Ωijk обобщенных дисклинаций определяет соответствующую неинтегрируемую часть кривизн DiΩjk . Контурный интеграл ви-Mx да ∫ DiΩjk dyk определяет разрывное поле дисторсии. Соответственно через антисиммет-M0

ричную часть кривизн ( - 1/2) D_i ^Ω _j Э_ijk определяется разрывное поле поворотов. Эти дефекты по определению являются классическими дисклинациями [16]. В средах с полями дисклинаций в общем случае не выполняется условие сохранения дефектов нижнего уровня – дислокаций [14], т.е. именно с наличием дисклинаций связана возможность генерации дефектов-дислокаций. Отметим, что в «бездефектных» средах Сен-Венана отсутствуют обобщенные дисклинации. При этом такая среда может иметь поле сохраняющихся дефектов-дислокаций. В теории сред Сен-Венана можно наряду с дисклинациями выделить скалярное поле скачков изменения объема θ^Ω – поры и тензорное поле скачков изменения формы – поле двойникования.

Отметим, что в работе [14] построена геометрическая теории дефектов. Там же дан существенно более подробный анализ полей дефектов различной сложности. Главный итог исследования кинематики сред с точки зрения построения математических моделей состоит в том, что кинематический анализ позволяет сформулировать связи и список аргументов функционала при построении математических моделей сред различной сложности вариационным методом.

Вариационный метод построения моделей сред

Для получения математической формулировки моделей сред с усложненной кинематикой используем кинематический вариационный принцип. Дадим общую формулировку обобщенных соотношений закона Гука. Далее предполагается, что рассматриваются линейные, обратимые процессы. Алгоритм построения модели сплошной среды сводится к следующему:

• 1.    На основе анализа кинематики сред устанавливаются возможный список аргументов функционала Лагранжа и набор кинематических связей.

• 2.    По кинематическим связям строится возможная работа внутренних сил, причем спектр внутренних сил определяется неопределенными множителями Лагранжа, на которых вводятся кинематические связи.

• 3.    Возможная работа внутренних сил преобразуется в линейную вариационную форму. Определяется список аргументов.

• 4.    Записываются условия интегрируемости линейной вариационной формы (условия существования потенциальной энергии) и формулы Грина.

• 5.    В предположении физической линейности и интегрируемости линейной вариационной формы строится потенциальная энергия. По сформулированной потенциальной энергии строятся физические соотношения (уравнения закона Гука) и лагранжиан.

• 6.    Из условия стационарности лагранжиана находятся уравнения Эйлера и естественные граничные условия.

Приведем некоторые конкретные примеры построения моделей сред различной сложности.

Модель классической теории упругости

Пусть в среде реализуются симметричные соотношения Коши: г _у = (1/2) ( R i , j+ R j , i) = Y , + (1/3) 05 , . Тогда каждой точке моделируемой среды приписываются девять степеней свободы: три компоненты вектора перемещений R_i и шесть компонент тензора деформаций г , . Симметричные соотношения Коши устанавливают связь между ними. Метод неопределенных множителей Лагранжа позволяет формально сохранить равноправие всех девяти степеней свободы при формулировке физической модели выбранной среды. Это достигается тем, что вводится тензор реактивных сил, обеспечивающих вводимые связи. Этот тензор является симметричным тензором в силу свертки тензора реактивных сил с симметричным тензором кинематических связей.

Тогда, в соответствии с кинематическим вариационным принципом, запишем вариацию возможной работы внутренних сил и используем интегрирование по частям. Получим

6U = JJJ а,6[г, - (1 / 2)(Ri,j + R, , ,)]dV = JJJ [a,6г, + a,,, 6R, ]dV + JJ(- a,n, )бRdF =

= JJJ [ тЛ , + (1/3)a„ 60 + a ,,,5R , ] dV + JJ ( -a_A> R , dF..        (11)

Здесь a ,

- компоненты симметричного тензора, т, = (1/2)(a ,+а,,)- (1/3)a „ 6,, n j – компоненты единичного вектора нормали к поверхности, ограничивающей рассматриваемое упругое тело, у, = 1/ 2(Ri,, + R,,,) - (1/ 3)06,, 0 = Rk,k .

Считая, что вариационная линейная форма (11) интегрируема (существует потен циальная энергия), получим: U = jjj UVdV + jj

U_rdF , U , = U , ( e „ , R k ) = U , ( y j , 6 , R - ),

U_F = U_F ( R k ). Для случая линейной среды, потенциальная энергия является квадратичной формой своих аргументов с учетом их тензорной размерности:

U = (1/ 2) jjj [2 ру j у j + (1 / 6)(2 р + 3 X ) 6 ² + 2 CR i R i ] d, + + jj ^{ Ann + B ( 5 у - n^ j )| RR j dF .

Последний интеграл описавает поверхностную энергию деформации и указывает на естественную анизотропию, связанную с нормалью к поверхности. Определяя внутренние силовые факторы с помощью формул Грина, получаем из (12), что в общем случае модель сплошной среды здесь допускает существование внутри объема внутренних силовых факторов типа напряжений оу =д U, /дRi j и объемных сил о i =д U, /дRi, а на поверхности - внутренних поверхностных сил Pi = 6 UF /дRi. Получим о»=р(R.,j+ RJ+XR-,.5,j, => = CR. (13)

Таким образом, показано, что тензор реактивных сил о _/у в (11), обеспечивающих вводимые связи (соотношения Коши), действительно является классическим тензором напряжений. На поверхности исследуемого тела справедливы следующие физические уравнения:

P = B R = AR n n + BR (5, - nn, ). (14) i ij j j i j j ij i j

Естественно считать, что р и X равны известным в теории упругости коэффициентам Ламе ( р - модуль сдвига). Постоянные A , B , C являются новыми упругими постоянными среды. При этом уравнения (13),(14) являются определяющими соотношениями для модели среды с симметричным тензором напряжений и упругими внутренними связями типа объемных и поверхностных винклеровских оснований. С учетом полученных определяющих соотношений нетрудно записать и вариационное равенство, определяющее математическую модель ( 5 L = 0, L = A - U , A - работа внешних сил на векторе перемещений R_k ).

Вопрос окончательной формулировки среды представляется весьма важным. Выбор окончательного списка физических постоянных в (12) должен диктоваться тем, что исследуемая модель среды не должна противоречить в принципе известным экспериментальным данным. Модель не должна противоречить известным экспериментальным фактам и ни для каких частных случаев. Для данной модели модель ньютоновской жидкости является частным случаем. Достаточно принять модуль сдвига равным нулю (р = 0). Известно и подтверждено экспериментально, что для однородного состояния при гидростатическом давлении выполняется условие 6 = const. С учетом закона Гука имеем для давления, p = const. Аналогично экспериментально доказано существование однородных состояний, в классической теории упругости с соотношением Коши, в частности, на примере растяжения и сдвига. Нетрудно видеть, однако, что вариационная постановка (12)-(14) не позволяет получить ни однородного решения, соответствующего гидростатическому давлению, ни однородных решений соответствующих растяжению и сдвигу, если только C * 0, A * 0, B * 0. Отсюда с необходимостью следует, что для корректного описания исследуемой модели следует принять C = 0, A = 0, B = 0. Таким образом, использование предложенного алгоритма приводит к вариационной постановке задачи теории упругости, если в качестве кинематических связей ввести симметричные соотношения Коши.

Модель простейшей несимметричной теории упругости

Рассмотрим теперь модель, где несимметричные соотношения Коши являются кинематическими связями:

d, = y, + ОД — ^kЭ, = Ri,j.

Покажем, что в результате удается построить простейшую теорию среды с несимметричным тензором напряжений. В соответствии с предлагаемым алгоритмом имеем:

5 U = JJJ о, 5( dj — Ri ч ) d' = JJJ о, 5(y, +1/305, -ю k Э,к - Ri,,) d, =

= JJJ [ g _s t _s 5y _s + (1/3) 0 „, 50 + ( -а „ Э ,к ) 5ю k -о,5 ^] d, + J ( -a „ n , ) 5 R i dF . (15)

Здесь о , - тензор множителей Лагранжа, описывающий спектр взаимодействий, соответствующих введенным кинематическим связям; т , = (1/2) ( c j I о ji ) - (1/3) о _kk 5_у

В результате, считая, что вариационная линейная форма (15) интегрируема (существует потенциальная энергия), можно получить:

и = JJJ U , d, + JJ ^dF , U , = U , ( d ” , R k ) = U , ( y , , 0 , ю k , R k ), U_F = U_F ( R k ).

Здесь так же, как и ранее, будем исключать из списков аргументов для плотностей потенциальной энергии вектор перемещений. Тогда рассматриваемая модель среды не будет противоречить известным экспериментальным данным. Окончательно потенциальная энергия имеет вид

U = JJJ U , dV , U , = U , ( d , ) = U , ( y , , 0 , ю k ) .

Условия интегрируемости линейной вариационной формы (существования потенциальной энергии) дают уравнения закона Гука о , = д U , / д d , . В соответствии с принципом Лагранжа ( 5 L = 0) имеем

5 L = JJJ (а₈, , + P ) 5 R i d, + g ( p^F -o , n , ) 5 R i dF = 0, где L = A - U , A = JJJ P^ R i d, + JJ P? dF , A - работа внешних сил, приложенных в объеме Р ' и на поверхности P iF .

Записанное вариационное равенство с учетом уравнений закона Гука дает математическую постановку задачи в перемещениях для классических сред с несимметричным тензором напряжений.

Рассмотрим модель сред с несимметричным тензором напряжений более подробно. Для физически линейной постановки плотность потенциальной энергии (16) является квадратичной формой аргументов, с учетом их тензорной размерности. Запишем Лагранжиан в следующем виде:

L = A - (1/ 2) JJJ [2 ^y , _ц + (1 / 6)(2 p + 3 X ) 9 ² + 4 /ю k ю k ] d, .

Здесь и k = - (1/2)[ R„ j -V JJJ R i , j dV ] Э„ , х

- новая физическая постоянная.

Отметим, что здесь в качестве одной из обобщенной координат принят псевдовектор иk, а не вектор поворотов иk = -(1/2)Ri,j Э^к. Это вполне допустимо, если будет доказано следующее условие эквивалентности: L(икик ) = L(ик ик ) .

V Л! и k dV = о.

Очевидно, что, по определению, и _к самоуравновешаны:

Запишем вариацию потенциальной энергии:

5 U = (1 /2) JJJ [2 py , 5y j + (1 /3)(2 ц + 3 X ) 656 + 4 _Хи _k 5и _k ] dV = = (1/2) JJJ [2 py j + (1/3)(2 ц + 3 X ) 65 j - 2 хи k Э^ ] 5 R_l,_JdV .

Применение формулы Грина a j = d U / d R i , j дает следующее уравнение закона Гука:

aj = 2pYj + |(2р + 3X)65, - 2ХиkЭ^ .

При этом легко убедиться, что тензор напряжений удовлетворяет следующему ус- ловию самоуравновешанности

V JJJ aijЭ^jkdV = 0- В результате можно записать пол- ную вариационную математическую постановку модели:

5L = JJJ [(ц + х)R,,j +(ц + X - х)Ri,, + P ]5R,dV +

+ JJ { P iF - [( Ц + х ) R i . , + ( ц - х ) R j , , +X R k , k 5 ] n, + [ V * JJJ x ( R , , j - R j , , ) dV ] " j } 5 R i = 0.

Получим необходимые и достаточные условия инвариантности рассматриваемой модели при преобразовании поворота системы координат. Положим R ‘ = R , + Q _nx m Э_пт , и и k = и _k + Q _k . Непосредственно из определения величины ю _k найдем

JJJ хиkиk]dV = JJJ хиkиkdV •

Учитывая записанное равенство, получим

L ′= A ′- U = ∫∫∫ P i ^VR i ′ dV + ∫∫ P i ^FR i ′ dF - U =

= ( JJJ P V RdV + JJ P F RdF ) + ( JJJ P V « , x „ Э„^У + JJ P F Q , x , Э„^Р ) - U =

= A - U - ( JJJ P?’X i Э ^^^dV + JJ P^Fx j Э_S k dF ) Q . = L - M k Q k .

Отсюда следует, что необходимым и достаточным условием инвариантности является равенство нулю момента внешних сил,

M k = 0, M k = JJJ P V X j Э ,k dV + g P^FX j Э ijk dF .

Действительно, из условия L' = L следует, что M_k Q _k = 0 . Так как Q _k - величина произвольная, то имеем доказательство достаточного условия: M_k = 0. Доказательство необходимости условия M_k = 0 очевидно: из M_k = 0 в записанном выше равенстве следует, что L' = L .

Таким образом, при выполнении необходимого и достаточного условия инвариантности M k = 0 имеет место равенство L ( to k to k ) = L ( to _k I Q ₀, to _k + Q ₀) и справедливо представление (17). Таким образом, простейший вариант несимметричной теории может быть сформулирован относительно «самоуравновешанной» части вектора поворотов. Это справедливо для односвязной области. Может быть сделано обобщение и на многосвязную область.

Модель среды с сохраняющимися дислокациями –среда Папковича–Коссера [17]

Кинематика такой среды описывается соотношениями (1) и (6)-(8). Для сред Папко-вича-Коссера непрерывными обобщенными переменными являются вектор перемещений среды R i , непрерывная и интегрируемая часть тензора дисторсии dy , непрерывная (но неинтегрируемая) часть тензора дисторсии d i i , и тензор плотности дислокаций в , .

Кинематические связи определяются несимметричными соотношениями Коши следующими уравнениями и неоднородными соотношениями Папковича:

Ri, , = di , d, = [YB + (1/3)6S5in-toiЭ^],m ЭПту = Bu .                    (18)

В соответствии с «кинематическим» вариационным принципом возможную работу внутренних сил на связях (18) следует представить в виде

8 U = JJJ [ о , 5 ( d “ - R , , ) + m^i , - d y , . Э„ , )] dV .            (19)

Здесь 5 U - возможная работа; о , и m , - тензоры множителей Лагранжа, которые имеют физический смысл реактивных силовых факторов, обеспечивающих выполнение соответствующих кинематических связей.

Представим 5 U в (19) как линейную форму вариаций своих аргументов. Используя интегрирование по частям в слагаемых, содержащих производные, получим

5 U = JJJ [ о , 5 d , + о , , , 5 R i + m , 5B , + m , , _т Э ^ 5 d i ] dV + ⁺ JJ ^[ -° Un^ ^Ri - m l n - Э п^ ^{5 d}ln ^{] dF} .

Тогда существует такой потенциал U (потенциальная энергия), при котором возможная работа 5 U в (20) является вариацией этого потенциала: 5 U = 5 U :

U = JJJ U , dV + JJ U_FdF , U , = U , ( d ” ;d i ; i , ), U_F = Uf ( d i ).     (21)

Отметим, что из списков аргументов для плотностей потенциальной энергии исключен вектор перемещений. Тогда рассматриваемая обобщенная модель среды с масштабными эффектами не будет противоречить в частном случае классической теории и известным экспериментальным данным.

Вычисляя вариацию 5 U , найдем:

∂ U        ∂ U        ∂ U       ∂ U

о = —V- , m =---, p = ——, M = —F = A d

⁴    d d i ^{0       y}   di ,       ⁱⁿ   d d ,       ⁴   d d ,      ^4nm '

Формулы (22) следует трактовать как обобщенные формулы Грина для объемных и поверхностных силовых факторов. Специально выделены новые постоянные A_ynm , описывающие спектр поверхностных свойств. Соотношения (22) позволяют записать лагранжиан и найти соответствующие уравнения Эйлера:

⁸ L = [Л К’ j • j + P V ) ⁸ R i - ( ™ in , - Э пт + P « ) ⁸ d j ] dV + + # [( P F -< Vj ) $ R, - ( M n + m , n „ Э пт ) 8 d “] dF = 0.

Отметим, что аналогично могут быть построены математические модели более сложных сред с микроструктурами, например среда Сен-Венана, кинематика которой была кратко изложена ранее.

Кратко обсудим далее модель среды с сохраняющимися дислокациями и некоторые ее частные случаи, представляющие интерес для приложений.

Модель среды с сохраняющими дислокациями [17]

Рассмотрим вновь плотности потенциальной энергии в объеме и на поверхности. Ограничимся рассмотрением физически линейных сред. Тогда U_V определяется как квадратичная форма своих аргументов:

• =    (d ⁰' d^a'H 1       d°d° + 2C¹² d°d^a + C²² d^ad^a + C³³ S S

U V U V v ^(u j ;^u j ; ij ) C ijnm^Uij^Unm ^{+ 2}C ijnm^U ij ^U nm ⁺ C ijnm^U ij ^U nm ⁺ C ijnm^ ij nm '      (^7

• 1.    Отметим кратко некоторые свойства данной модели. Структура тензоров модулей упругости C ijqm , p , q = 1,2 в (24) определяется их разложением по изотропным тензорам четвертого ранга, построенным как произведение пары тензоров Кронекера со всеми возможными перестановками индексов:

pq       pq             pq              pq

С ijnm C 1 ⁸ ij ⁸ nm ⁺ C 2 ⁸ in ⁸ jm ⁺ C 3 ⁸ im ⁸ jn ^{( p} , ^q 1,^{2 )} -

Очевидно, что модули C j _m определяют классические «неповрежденные» модули упругости, модули C i * ² _m и C ij^m дают учет поврежденности (полей дислокаций). «Поврежденные» эффективные модули упругости могут быть явно записаны через эти физические параметры. Доказывается, что «поврежденные» модули упругости всегда меньше неповрежденных. Наконец, новый модуль упругости C j _m имеет размерность отличную от размерности классических модулей упругости C_i ¹ _j ¹ _nm , и определяет масштабные эффекты. Для изотропного тела упругие модули можно записать через аналоги коэффициентов Ламе X ^pq , р ^pq и модули х ^pq , определяющие несимметричность тензора напряжений,

С = Х ^pq 8_и8 nm + ( р ^pq +Х ^pq ) 8„ 8 jm + ( р ^pq -х ^pq ) 8 m 8 jn , C jnqm = C iqnpm .   (25)

Можно показать [17], что часть объёмной плотности потенциальной энергии, связанная с псевдотензором-источником дислокаций

ΞΞ    ΞΞ c 33 a ..a = ( c 33 э,э, ) -^ia^nc = c 33, , ia^n^. ijnm ij nm (ijnm^abj^cd^m)                  'funded               ,

∂xb ∂xd          ∂xb ∂xd определяет быстроменяющуюся, локальную часть потенциальной энергии дислокаций. Остальная часть объёмной плотности потенциальной энергии является медленно ме- няющейся и определяется как сумма потенциальных энергий трех типов дислокаций: γ -дислокаций, θ -дислокаций и ω -дислокаций. Следовательно, медленно меняющаяся часть энергии деформации не содержит перекрестных членов от указанных типов дислокаций и является аддитивной формой относительно компонент свободной дисторсии. Отметим, что для приближенных оценок, вероятно, можно пренебречь локальной, быстро изменяемой частью энергии. При этом действительно имеет место аддитивность в разложении плотности потенциальной энергии относительно компонент свободной дисторсии. Это обстоятельство может использоваться в качестве обоснования предложенной выше новой классификации типов дислокаций.

Запишем уравнения закона Гука (22) для объёмных силовых факторов:

ij ijnm n ^, m

-I

12 Ξ ijnm nm ,    pij

-I

21             22 Ξ                 33

ijnm n ^, m ijnm nm ^, ij ijnm nm ^.

Обобщенные импульсы σij , pij , mij в (26) зависят не только от обобщенных скоростей Rn ,m , Ξij , но и от обобщенных координат diΞj . Из (26) следует, что наряду с тензо- ром напряжений σij в таких средах имеют место дополнительные силовые факторы – «дислокационные» напряжения pij [10]. Положим, что Сi1jn2m = 0 . В этом случае общая краевая задача распадается на краевую задачу относительно перемещений Ri и краевую задачу относительно свободной дисторсии d iΞj . При этом краевая задача относительно перемещений при дополнительном предположении χ11 = 0 (теория упругости с симметричным тензором напряжений) совпадает с классической теорией упругости. Тогда силовой фактор σij приобретает смысл классических напряжений. Соответственно силовой фактор p ij приобретает смысл винклеровской реакции в уравнениях равновесия моментных напряжений. При Сi1jn2m ≠ 0 происходит взаимное возмущение классического поля перемещений и чисто дислокационных состояний. Перекрестные члены в уравнениях закона Гука для σij и pij и отражают эти возмущения. Эти же соображения дают алго- ритм решения общей краевой задачи методом последовательных приближений.

Для гладкой поверхности всегда существует естественно выделенное направление – нормаль к поверхности. Уравнения закона Гука для внутренних силовых факто- ров на поверхности должны иметь трансверсально-изотропный характер, и в результате кинематические факторы, связанные с нормалью к поверхности и с касательной плоскостью, будут входить в эти уравнения закона Гука неравноправно.

Рассмотрим выражение для поверхностной части возможной работы. Первое сла- гаемое в нем полностью соответствует классическому представлению. Оно появляется в результате интегрирования по частям выражения

∫∫∫

[ σ _ij δ ( R_i , _j )] dV в равенстве (20).

Второе слагаемое в выражении поверхностной части возможной работы является неклассическим, обязано своим появлением «кинематическому» вариационному принципу построения модели и связано с поверхностной энергией адгезии U F . Доказано ут- верждение [17] о том, что работа моментных напряжений (23) на поверхности тела совершается не на всех девяти компонентах тензора свободной дисторсии diΞn , а только на шести из них diΞk (δkn - nknn):

m n Э δ d ^Ξ dF = m n Э δ d ^Ξ ( δ  - n n ) dF .

ij m nmj in                  ij m nmj ik kn k n ^.

В результате поверхностная плотность потенциальной энергии имеет вид

Up = (1/2)Л.. d" (5 -п п ^"(5 -п n V

F \    / ijnm np\ pm ^р mz iqV q) ‘q j) •

Поэтому список аргументов поверхностной плотности потенциальной энергии в (21) уточняется. Уточненный список аргументов определяется теперь шестью «плоскими» компонентами тензора свободной дисторсии d m (5 _pm - n_pn_m ): U F = U F ( d ik (5 _kj - n_kn_j )).

Выражение для плотности поверхностной потенциальной энергии приобретает вид

Up (5 -nnYb-nnAd d^a~0 /2)Z d^а d^a.

F               ijnm pm p m qj q j np iq               ijnm nm ij ^.

Адгезионным модулям может быть дана четкая физическая трактовка, и они выражаются для данной модели через четыре адгезионных параметра p F , X F , х F и 5 F (адгезионные модули):.

A jnm = ^{[ X} F ^{( 5} ij — ⁿi n j)^{( 5} nm — n n n m ) + ⁵ F n i n n ^{( 5} jm — n j n m ) +

+ ⁽ P F + X F ^{)( 5} in — n i n n ^{)( 5} jm — n j n m ) + ⁽ P F -X F ^{)( 5} im — n i n m ^{)( 5} jn — n j n n XL

Коэффициенты (p F +X F ) определяют поверхностное натяжение, p F и х F определяют в совокупности энергию формоизменения и энергию скручивания в плоскости, касательной к поверхности; величина 5 F связана с определением энергии изгиба поверхности. В общем случае лагранжиан имеет вид

Z, = Л — {С¹¹ R , R,-2C¹² R , d ^a + С²² d ^a d^a + С³³ E EAdV- ijnm n ^, m i ^, j        ijnm n ^, m ij ijnm nm ij ijnm nm ij

• -(1/2)$ A * d^a d^a dF. ijnm nm ij ^.

Напомним, что на основе кинематического анализа предложена классификация дислокаций, позволяющая выделить три типа дислокаций: Y-дислокации, О -дислокации, ю -дислокации. Эта классификация, дает новую как физическую, так и кинематическую трактовку дислокаций, так как отражает связь дислокаций с формоизменением - у, с изменением объема О (пористость) и со скручиванием ю (вихри или спины). Каждой точке среды с сохраняющимися дислокациями приписывается двенадцать степеней свободы: три компоненты перемещений Ri, три компоненты вращений юa и шесть компонент деформиции a ijj

= Y a + ¹ 0^a 5.. ij ₃ ij

Предложенная классификация

фактически позволяет прогнозировать и частные случаи сред с сохраняющимися дислокациями, когда в среде доминируют лишь один или два типа дислокаций. В таких частных моделях удается сократить количество степеней свободы, что существенно облегчает исследование отдельных свойств сред с сохраняющимися дислокациями. Приведем некоторые возможные примеры частных моделей:

Частный случай 1. Доминирующими являются дислокации, порожденные только свободными поворотами юa. Это «классический» вариант модели сред Коссера с ше стью степенями свободы Ri и юa. В такой среде ya = 0 и 0a = 0. Тензор свободной дисторсии определяется соотношением dj = -юa Эук.

Частный случай 2. Доминирующими являются дислокации, порожденные только свободным изменением объёма 0a. Это модель пористой среды с четырьмя степенями свободы Ri, 0“ . В такой среде ю“ = 0 и у “ = 0. Тензор свободной дисторсии определяется соотношением dy = (1/3)0“5у.

Частный случай 3. Доминирующими являются дислокации, порожденные только свободным изменением формы у “ • Это модель среды с двойникованием с восемью степенями свободы R i , у “ • В такой среде to “ = 0 и 0 “ = 0. Очевидно, что при этом ΞΞ i/        ' У

Отметим также, что использование кинематического вариационного подхода и детальный анализ граничных условий дали возможность сформулировать непротиворечивую и согласованную краевую задачу для сред с сохраняющимися дислокациями с девятью граничными условиями в каждой неособенной точке поверхности. Следует напомнить, что при последовательной вариационной формулировке задачи всегда достигается согласованность математической постановки. Порядок задачи фактически определяется количеством независимых граничных условий. Отметим, что в наиболее последовательной теории сред с микроструктурами Миндлина[10] краевая задача содержит двенадцать краевых условий, что не соответствует общему порядку разрешающих уравнений. По-видимому, это связано с тем, что в работе [10] не был установлен вид поверхностной плотности потенциальной энергии, соответствующий адгезионным взаимодействиям, и не был дан анализ работы этих поверхностных взаимодействий.

Некоторые частные модели сред с сохраняющимися дислокациями

Рассмотрим некоторые частные случаи общей теории сред с сохраняющимися дислокациями.

Классическая среда Коссера [17]

Рассмотрим частный случай сплошной среды, когда тензор свободной дисторсии d“ =y“ + (1/3)0“5ij -to“Э/ук определяется только свободными поворотами, а свободные деформации равны нулю у“ = 0 , 0“ = 0. В этом случае имеем среду с шестью независимыми степенями свободы - тремя компонентами вектора перемещений Ri и тремя компонентами псевдовектора свободных поворотов to“. Каждая точка такого континуума ведет себя как абсолютно жесткое тело: может смещаться и поворачиваться, в отличие от точек классической среды Коши, которые могут только смещаться. Такая кинематика является характерной для классических сред Коссера. Построим такой частный случай теории сред с сохраняющимися дислокациями и сравним соответствующие краевые задачи. Тензор свободной дисторсии здесь определяется соотношением d = (—to “ Э/k ).                                  (28)

Псевдотензор дислокаций “ у записывается следующим образом:

“ у = -to “ , m Э пк Э пту =-to k , m ( 5 km 5 у — 5 у 5 m ) = ( to / , , —to “ , _к 5 у ) # 0.

Таким образом, в модели сред Коссера тензор плотности дислокаций отличен от нуля. Нетрудно убедиться, что выполняется и закон сохранения дислокаций. Следовательно, теория сред Коссера является частным случаем теории сред с сохраняющимися дислокациями. Тогда с учетом формул (22), (23), (28) Лагранжиан сред Коссера приобретает следующий вид [17]:

L = A - (1/2) JJJ {[(1/3)(2 р ¹¹ + Xⁿ ) 5 , 5 nm +

+ 2 p^H (( 1 /2)( 5„ 5^ + 5 m 5 , ) - 1/3 5 , 5 nm )] R , m R i , , +

+ 4X11ok ° + 8x12 о o of + 4/22 of of +

+ [(2 p ³³ + 4 X ³³) 5 , 5 nm + ( p ³³ +x ³³) 5_m 5 m + ( p ³³ —X ³³) 5 m 5 , ] o f , , o f , m ]} dV -

• - (1/2) JJJ [ 5 F ( 5 pq - n p n q ) + 4 x F n_pn_q ] o f o'dV .

Общий вид Лагранжиана (и потенциальной энергии) позволяет записать уравнения закона Гука для сред Коссера:

а„ = 9 UV   = 1 (2Ц11 + 3X11) Кк ,к 5,- + 2p11[1 (К,,,+ R,. „ ) - 1 Rk ,k 5,] + ij                                          kk ij                 i j ji          kk ij

^{д (} R ., , ) ^{3           23}

+ 2x"[j( R i , , - R , , i )] - 2x" o f Э_№ ,

P i =2 U V 7 = - 2 x ' ^! R n , . Э„О 4 x ²² o f , d ( o i )

m , =      '    = (2 p ³³ + 4 X ³³ ) o f , k 5 , + ( p ³³ + x ³³ ) o f , , + ( p ³³ - X ³³ ) o f , , ,

^{d ( o} i ,

AU       -

Mi =---F~ = nFof (5„ i /(o f)         i y

^- nn , J ^{+ 4}X F ^{( o} f n j J n .

Вариационное уравнение теории сред Коссера приобретает вид

5 L = JJJ

В-< д х,

+ РГ ^5Ri + у

'/ m u < д х ,

^- Pi 5ofу

dV +

+ JJ(PF - оyn,■ )5RidF - JJ(mi,n, + Mi)5ofdF = 0 •

С учетом (29) уравнения равновесия, уравнения моментов и граничные условия в (30) можно переписать в кинематических переменных. Разрешающие уравнения имеют вид

(p11 + x11 ]f AR. - - 9^RA-1 + (2p11 + X11 )^^R^ + 2x12     Эпт. + PV = 0, v 1 i   дx,дxf     v           удx,дxf          дxm

m

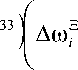
^2  5 A

Ют- ^{д x}i ^{д x}k J

+ 4 ( p ³³

5 ² tof      „ _и SR

= 0.

- 4x 22 o f+ 2x12 —n Эnmi д x,д x, ikm

Соответственно связанная краевая задача (29)-(30) дает шесть граничных условий в каждой неособенной точке поверхности тела.

Теория пористых сред [17]

Рассмотрим следующий частный случай общей теории, в котором доминируют только 0 -дислокации. В этом случае 0 “ * 0 , у “ = 0 , го “ = 0 . Имеем d j = (1/3) 0 “ 5 , . Псевдотензор-источник дислокаций записывается следующим образом:

“ j = d „ , т Э пт, = ( — 1/3) 0 “ , к Э jk * 0, “ , , , = 0.

Таким образом, в представленной теории пористых сред тензор плотности дислокаций отличен от нуля, следовательно, она также является частным случаем теории сред с сохраняющимися дислокациями. Для этой теории Лагранжиан принимает вид[17]:

L = A - (1/2) JJJ {2 ц ¹¹ у j y 0 +

+ (1/3)(2 ц ¹¹ + 3 Х ¹¹) 0 ⁰ 0 ⁰ - (2/3)(2 р ¹² + 3 Х ¹²) 0 ⁰ 0 “ + (1/3)(2 ц ²² + 3 Х ²²) 0 “ 0 “ +

+ (4/9) х ³³ 0 “ „0 “„ } dV- 2 ff {(4/9)( ц F + Х F ) 0 “ 0 “ } dF .

В соответствии с (22) уравнения закона Гука теории пористых сред принимают вид:

° , = UF = 2 А , + ^н” + 3Х") 0 ⁰ 6 , - (1/3)(2 ц ¹² + 3 Х ¹²) 0 “ 6 , , ^{д ( R}i , j )                ³

Ркк = U = -(1 / 3)(2ц12 + 3Х12 )00 + (1/ 3)(2ц22 + 3Х22 )0“, ∂θΞ mk = dUV = (4/9)x 330“,,. k d(0“,к )        M k

Отметим, что и здесь, как и в теории Коссера, определяются и дислокационные напряжения, и моменты (несмотря на то, что эта среда с симметричным тензором напряжений Коши). Запишем вариационное равенство теории пористых сред:

5 L = JjJ {[ ц ¹¹ A R . + ( ц ¹¹ + Х ¹¹) R j , , - (1/3)(2 ц ¹² + 3 Х ¹²) 0 “„+ p^V ] 6 R . + + (1/3)[(4/3) x ³³ A0 “ - (2 ц ²² + 3 Х ²²) 0 “ + (2 ц ¹² + 3 Х ¹²) 0 0 ] 60 “ } dV +

+ ff { P F - [ ц ¹¹ ( R ,,.) п . + ц ¹¹ ( R ,,.) п , +Х ¹¹ ( R k , к ) п. -

- (1/3)(2 ц ¹² + 3 Х ¹²) 0 “ n . ]} 5 RdF -

- (4 / 9) ff [ х ³³ ( 0 “ , . ) n . + ( ц ^F + Х ^F ) 0 “ ] 50 “ dF = 0

Вариационное уравнение (31) дает полное описание краевой задачи теории пористых сред: имеются четыре разрешающих уравнения относительно четырех искомых функций R . и 0 “ и четыре граничных условия в каждой неособенной точке поверхности.

Аналогично может быть рассмотрена и теория сред с двойникованием, которая представляет значительный интерес с точки зрения моделирования фазовых превращений. В этом случае 0“ = 0 и го“ = 0, а тензор свободной дисторсии приобретает вид: dj = у“. Псевдотензор-источник дислокаций записывает следующим образом: “, = у“,т Эпт,, и “,,, = 0. Следовательно, теория сред с двойникованием является частным случаем теории сред с сохраняющимися дислокациями.

Достаточно подробное описание и анализ теории сред Коссера, теории пористых сред и сред с двойникованием даны в недавней работе[17].

В заключение кратко остановимся на модели среды Аэро-Кувшинского, которая является частным случаем теории сред Коссера.

Модель сред Аэро–Кувшинского [17]

Мо дель сред Аэро-Кувшинского [13] строится с использованием гипотезы о существовании кинематической связи между спинами и вихрями перемещений. Гипотеза Аэро-Кувшинского может быть записана в виде

Ю = -X R p , q Э pqk -                                   (32)

При такой «жесткой» гипотезе спины агебраически могут быть исключены из лагранжиана сред Коссера. Таким образом, в модели Аэро - Кувшинского основными неизвестными могут быть выбраны только перемещения и относительно них может быть сформулирован Лагранжиан. При этом плотность дислокаций в модели Аэро-Кувшинского отлична от нуля. Ненулевые спины ю Е связаны гипотезой (32) с перемещениями. Они определяют соответствующий ненулевой псевдотензор-источник дислокаций в теории Аэро-Кувшинского: Е _у = ⁽ _Ю^Е —го Ё , k ⁵ _y ) = x R p , iq Э pq * 0

Таким образом, в модели сред Аэро - Кувшинского тензор плотности дислокаций отличен от нуля и выполняется закон сохранения дислокаций Е , , , = 0. Следовательно, теория сред Аэро-Кувшинского является частным случаем теории сред с сохраняющимися дислокациями. Вариационное уравнение модели Аэро - Кувшинского нетрудно получить из вариационного уравнения модели Коссера с учетом дополнительно введенной кинематической связи (32)[17]

5 L = [JJ [°, . , -x ( m. . , m, - P k , , ) Э » + P ) 5 R . dV +

+ Л [( P F ^-a ,ⁿj ^-X ⁽ mb , , m ^- P . ) H Ч ^п, Э_№ -x ⁽ m j n j ⁺ M ), q ( 8 q- п ^ п,) Э , ^{) 5} R ⁺

⁺ X ⁽ m ij n j ⁺ M i ) ⁿ/) k ^{5 ( R}p , q ^{( 5} pi- n p ndn q ^{)] dF} = ⁰

где используются следующие обозначения:

Ц V =- ( x ¹²/ x ²²)( m . E , m Э . + p^ Э^ ,

Ц ^F =^{- (} X ^{12 /} X ^{22 )(} Mi n ^{+ m}ij n m Э пт,) ^Эipk ^{( 5} pn - n p n n )•

Заметим, что характерной чертой модели сред Аэро - Кувшинского является то, что в каждой неособенной точке поверхности вариационное уравнение дает не шесть (как в модели Коссера), а пять граничных условий, ибо п.п, Э_ijk = 0, и поэтому

( Ц F n j Э jk ) 5 ( R , , q n q ) = ( Ц ^ П , Э _ук ) 5 ( R p , q 5 p, n_q ) =

= ⁽ Ц ^Fkⁿ j ^Э ,к ^{) 5 ( R} p , q ^{( 5} p. ^{- n} p ⁿ. ^{+ n} p ⁿ. ) ⁿ q ) = ⁽ Ц ^F k ⁿj ^Э_У к ^{) 5 ( R} p , q ^{( 5} pi - ⁿ p ^ ) ⁿ q )

Таким образом, вариационное уравнение сред Аэро - Кувшинского приобретает следующий окончательный вид:

5 L = jJJ ( -ц V , , Э_ук + a , , , + P^V ) 5 R . dV +

⁺ ff ^[( P^{F -a} jⁿ, +Ц ^Vkⁿ ,^Э ijk -Ц ^F ’ q ^{( 5} qj - ⁿqⁿj)^Э ijk ^{) 5 R}i ⁺

+ ( Ц F n^_yk ) 5 R p , q ( 5 p. - n p n . ) n q )] dF = 0.

Модель Аэро – Кувшинского как прикладная модель интересна по следующим причинам:

• 1.    Модель Аэро – Кувшинского сформулирована только в перемещениях, что удобно и наглядно.

• 2.    Основные свойства среды описываются уравнениями в перемещениях, однако краевая задача является более простой.

• 3.    «Жесткая» гипотеза Аэро – Кувшинского о пропорциональности спинов и вихрей позволяет перенести эту гипотезу на общий случай сред с сохраняющимися дислокациями и сформулировать обобщенную гипотезу Аэро – Кувшинского в следующем виде:

d j = aR k , k 5 _y . + bR . , j + cR j , _z .                              (33)

Гипотеза Аэро – Кувшинского в виде (33) дает возможность сформулировать прикладную теорию сред в перемещениях с шестью граничными условиями в каждой неособенной точке поверхности тела. Именно с использованием обобщенной гипотезы Аэро – Кувшинского был развит простейший вариант континуальной теории межфазных взаимодействий [7], [8], [18], [19]. Эта теория позволила смоделировать и объяснить известные масштабные эффекты в механике мелкодисперсных композитов, определяемые когезионными и адгезионными локальными взаимодействиями.

Заключение

В работе исследуются модели континуальных сред с микроструктурой, которая определяется кинематикой различной сложности. Строятся корректные математические модели, включающие определяющие уравнения, разрешающие уравнения и граничные условия. Для формулировки моделей используется кинематический вариационный принципа, согласно которому общий вид функционала энергии для исследуемой среды находится по заданным кинематическим связям. При этом спектр внутренних взаимодействий полностью определяется системой кинематических связей, реализующихся в среде. Развивается алгоритм построения моделей сред с обобщенной кинематикой. Приводятся примеры получения математических моделей сред, начиная с классической симметричной теории упругости и вплоть до усложненных континуальных моделей сред, учитывающих масштабные эффекты в объеме и на поверхности тел. Предложен общий вариант теории сред с сохраняющимися дислокациями, который обобщает известные модели сред с микроструктурой Миндлина, Тупина, Коссера и пр. Рассматриваются частные модели сред, представляющие интерес с точки зрения приложений.