Вариационная интерпретация задачи расчёта функции эйконала из условия формирования заданного распределения освещённости

Задача расчёта оптического элемента из условия формирования заданного распределения освещённости в некоторой области относится к классу обратных задач неизображающей оптики и является крайне сложной. В большинстве случаев данная задача сводится к решению нелинейного дифференциального уравнения эллиптического типа. Наиболее простым уравнением данного типа является уравнение Монжа –Ампера, которое описывает обратную задачу расчёта функции эйконала светового поля из условия фокусировки в заданную область в параксиальном приближении [1]. Данная задача является важной при расчёте дифракционных оптических элементов [2]. Кроме того, по функции эйконала может быть восстановлена рефракционная или отражающая оптическая поверхность, что позволяет по функции эйконала рассчитать преломляющий или отражающий оптический элемент [3].

В последние годы были предложены методы расчёта оптических поверхностей, основанные на численном решении уравнений типа Монжа –Ампера конечно-разностными методами [4–9]. В рамках данных методов производные заменяются конечно-разностными аппроксимациями и решение уравнения сводится к решению системы нелинейных уравнений относительно значений искомой функции, описывающей оптическую поверхность и заданной на некоторой сетке. В зависимости от сложности задачи, система содержит от нескольких тысяч до нескольких десятков тысяч нелинейных уравнений. Для решения полученной системы используются итерационные методы, например, метод Ньютона. Общим недостатком такого подхода является высокая вычислительная сложность задачи решения системы нелинейных уравнений, а также выбор начального приближения для решения системы.

Другой перспективный подход к решению задач неизображающей оптики состоит в формулировке обратной задачи как задачи Монжа – Канторовича о перемещении масс со специальной функцией стоимости [1]. Действительно, в дискретном варианте задача о перемещении масс (ЗПМ) может быть сформулирована как линейная задача о назначениях (ЛЗН) [10]. Для решения ЛЗН предложены эффективные алгоритмы (венгерский алгоритм [10], алгоритм Джонкера – Волгенанта [11], алгоритм аукциона [12]), решающие задачу за полиномиальное время. В ряде случаев решение задач неизображающей оптики через решение ЛЗН оказывается значительно более эффективным с вычислительной точки зрения, чем численное решение уравнения типа Монжа –Ампера [1]. Вид функции стоимости определяется типом решаемой задачи. В частности, для обратной задачи расчёта функции эйконала в параксиальном приближении функция стоимости является квадратичной [1]: p _par( u , v ) = ( u — v )². Здесь предполагается, что искомая функция эйконала и заданное распределение освещённости заданы в двух параллельных плоскостях z =0 и z = f , где u = ( u 1 , u 2 ) и v = ( v 1 , v 2 ) – декартовы координаты в данных плоскостях. В работах [1, 13] авторов данной статьи было показано, что в задаче расчёта функции эйконала в общем непараксиальном случае функция стоимости не является квадратичной, а равна расстоянию

P ( u , v ) = 7 f ² + ( u - v )²

между точкой u = (u1, u2) исходной плоскости, в которой задана функция эйконала, и точкой v = (v1, v2) плоскости фокусировки. В настоящей статье этот результат обобщён на случай, когда искомая функция эйконала и требуемое распределение освещённости заданы на некоторых криволинейных поверхностях S и W. Доказательство основано на вычислении первой вариации функционала «стоимости», описывающего ЗПМ с неквадратичной функцией стоимости р (u, v) и зависящего от лучевого отображения между указанными поверхностями S и W. При этом показано, что условие равенства нулю первой вариации данного функционала равносильно тому, что лучевое соответствие сохраняет энергию и задаётся функцией эйконала на поверхности S.

Данный результат, помимо теоретической значимости, имеет ряд важных практических применений (не рассматриваются в рамках данной статьи). Во-первых, как отмечено выше, это позволяет свести решение обратной задачи функции эйконала, заданной на криволинейной поверхности, к решению ЛЗН. Во-вторых, установленные вид первой вариации и градиента функционала стоимости дают возможность рассчитывать функцию эйконала, обеспечивающую формирование заданного распределения освещённости, с помощью методов градиентного спуска.

1.    Формулировка задачи расчёта функции эйконала на поверхности

Пусть имеются две поверхности S и W, заданные уравнениями z=g (x, y), (x, y) eQeR2 и z =f(x, y), (x,y) e R2 в декартовой системе координат x = (x,y, z). Будем считать, что поверхность W расположена над поверхностью S: f(x,y)> g(x,y) (рис. 1). Далее будем обозначать координаты (x, y) точек на поверхностях S и W векторами u = (и 1, и2) и v =(v 1, v2) соответственно. Для дальнейших рассуждений нам будет удобно по- лагать, что точки u и v заданы в отдельных двумерных системах координат (рис. 1).

Будем считать, что на первой поверхности заданы функция эйконала Ф ( u ) и функция распределения освещённости E ₀( u ). Обозначим p ( u ) = ( p 1 ( u ), p ₂( u ), p ₃( u )) вектор луча для среды с показателем преломления n = 1, определяемый функцией эйконала Ф ( u ), заданной на поверхности S . Согласно уравнению эйконала, вектор луча p ( u ), исходящего из точки поверхности S , является единичным и определяется через производные функции эйконала из следующей системы уравнений [14]:

дФ(u)                 5g (и)

= p i ( u ) + p 3 ( u ) • —^, д u i                         д u i

<

дФ(u)                 ag (u)

— = p2 (u ) + p3 (u)• —---, ди 2                     ди 2

p 3 ( u ) = V¹ “ ( p ( u ) ) ² “ ( p 2 ( u ) ) ² .

Функция эйконала Ф ( u ) задаёт «лучевое» отображение Р ф : u ^ v следующим образом. Образом точки u e В является точка v , соответствующая пересечению луча, исходящего из точки ⁽ u , g ⁽ u )) e S , с поверхностью W (рис. 1).

Определение . Пусть задано некоторое отображение P : 0^0 . Будем говорить, что P интегрируемо, если существует функция Ф ( u ) на В такая, что P = Р _ф .

Сформулируем условие интегрируемости в удобном для дальнейших выкладок виде. Отображение P переводит точку ( u , g ( u )) поверхности S в точку ( P ( u ), f ( P ( u ))) поверхности W . Рассмотрим вектор t = ( P ( u ) — u , f ( P ( u )) — g ( u )). Обозначим его длину за р ⁽ u , ^P ( u )), разделим на неё и получим вектор единичной длины:

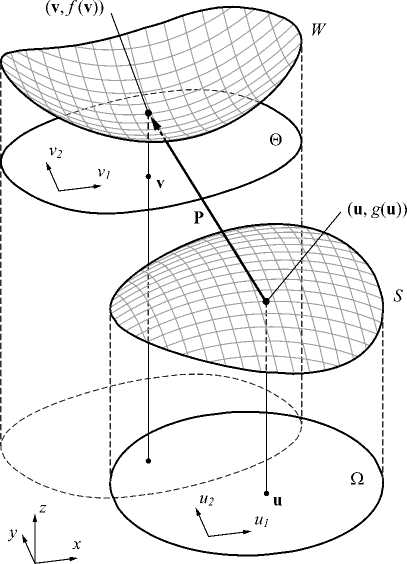
Рис. 1. Геометрия задачи p (u)=

( p ( u ) - u , f ( p ( u ) ) - g ( u ) ) p ( ^u , ^{p ( u} ) )

Если отображение P задаётся функцией эйконала Ф (u), то из (1) получим условие интегрируемости в виде:

VФ ( u ) =

^{P ( u ) - u} + v g ₍ u ) • f ^{( P ( u ) )-} g ( u ) p ( u , P ( u ) )          '    p ( u , P ( u ) )

(2a)

где V = (d/dи 1, d/dи2) - оператор градиента. Отметим, что в силу симметричности задачи относительно поверхностей S и W условие интегрируемости для обратного отображения P-1 имеет аналогичный вид:

V¥ ( v ) =

v - P ^{- 1}( v ) + p ( P ^{- 1}( v ), v )

(2b)

^+v f ( v ) •

^{f (} v ) ^- g ( ^{p 1(} v ) )

p ( P 1 ( v ), v )

Здесь ^ ( v ) - это эйконал на второй поверхности, обеспечивающий формирование распределения освещённости E o ( u ) на первой поверхности.

Сформулируем задачу расчёта функции эйконала Ф ( u ) из условия формирования заданного распределения освещённости E ( v ), v e@c R² на второй поверхности W (рис. 1).

Требуется найти функцию эйконала Ф ( u ), задающую отображение Р _ф : 0 ^ 0 такое, что для любого измеримого множества тс0 должно выполняться условие сохранения светового потока

J E о ( u )d S = J E ( v ) d W ,                     (3)

РДш)         m где dS = ^ 1 + |^Vg (u)]2du и dW = ^ 1 + |^Vf (v)]2dv - дифференциалы площади поверхностей, а du и dv обозначают du 1du2 и dv 1dv2 соответственно. Делая во втором интеграле в (3) замену v = Рф(u), получим

J E o ( u ) G ( u ) d u =

Р ф1И

= J E ( Р ф ( u ) ) F ( Р ф ( u ) ) J P ф ( u ) d u , Рф' ( ™ )

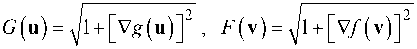
, a

J _{Р ф} ( о )  - якобиан преобразования координат

( v 1 , v 2 ) = ( P 1,ф ( u ) - P 2,ф ( u )):

J Р ф ( ^u ) =

dр1,Рф 5p2,Рф   5р1,Рф 5p2,Рф du 1   du 2     du 2   du 1

В дифференциальном виде условие сохранения светового потока (4) примет вид

E о ( u ) G ( u ) = E ( P ф ( u ) ) F ( P ф ( u ) ) J p ф ( u ) ,    (5a)

или, в терминах обратного отображения,

E о ( Р ф ¹ ( v ) ) G ( Р ф ¹ ( v ) ) J Р ф1 ( v ) = E ( v ) F ( v ) . (5b)

Таким образом, задача расчёта функции эйконала ф ( u ) сводится к решению уравнения (5a), где отображение Р _ф ( u ) определяется уравнениями (1).

• 2.    Задача о перемещении масс

Покажем, что сформулированная задача расчёта функции эйконала может быть сформулирована как задача Монжа-Канторовича о перемещении масс (ЗПМ) с функцией стоимости

• p ⁽ u , v ) = _v ( v u ) 2 ■ ( / ( v ) g ( u ) ) 2 ,                   ⁽⁶⁾

равной расстоянию между соответствующими точками поверхностей S и W . Для формулировки данной ЗПМ введём понятие плана (плана перевозки). Планом будем называть некоторое биективное дифференцируемое отображение P : 0^0 , сохраняющее меру (световой поток) в смысле соотношения (5а). Определим следующий функционал на множестве планов:

I ( P ) = J p ( u , P ( u ) ) G ( u ) E 0 ( u ) d u .               (7)

Решение ЗПМ состоит в определении отображения P , минимизирующего (или максимизирующего) функционал (7) при условии (5а). Согласно [15] для отыскания экстремума функционала I ( P ) при условии (5) (при ограничении типа равенство) можно использовать метод множителей Лагранжа. Согласно этому методу условный экстремум функционала (7) является безусловным экстремумом следующего функционала:

G ( P , X ) = J [p ( u , P ( u ) ) G ( u ) E o ( u ) +

0                                        (8)

• + X ( u ) ( E ( P ( u )) F ( P ( u )) J p ( u ) - E 0 ( u ) G ( u ) ) ] d u .

Отметим, что в статье [16] (параграф 2.1) приведено вычисление вариации аналогичного функционала с квадратичной функцией стоимости. Мы проделаем вычисление значительно проще, сначала преобразовав данный функционал.

Перейдём во втором слагаемом функционала (8) к интегрированию по переменной v (то есть сделаем замену переменной u = P ^-1( v )) и сделаем подстановку X ( u ) = ц ( P ( u )). В результате получим новый функционал, зависящий от функций P и ц :

F ( P , ц ) = J p ( u , P ( u ) ) G ( u ) E o ( u )d u +

+ J ц ( v ) ( E ( v ) F ( v ) -                               (9)

• - E 0 ( P ^{- 1} ( v ) ) G ( P ^{- 1} ( v ) ) J p -1 ( v ) ) d v .

Выделяя в (9) интеграл от слагаемого, содержащего якобиан обратного отображения, и переходя в нём к интегрированию по переменной u , получим следующую удобную для дальнейшего анализа форму функционала, не содержащую якобиан и обратное отображение P ^-1:

F ( P , ц ) =

• = J [p ( u , P ( u ) ) -ц ( P ( u )) ] G ( u ) E o ( u )d u +       (10)

+ J ц ( v ) E ( v ) F ( v ) d v .

Вычислим первые вариации функционала F ( P , ц ) по P и ц . Вариация по ц вычисляется сразу из формулы (9). Действительно, если ц_E ( v ) = ц ( v ) + E-p ( v ), то

• 5 ц F ( P , ц ) = e J [ E ( v ) F ( v ) -

• - E 0 ( P ^{- 1} ( v ) ) G ( P ^{- 1} ( v ) ) J p -1 ( v ) ]n ( v ) d v .

Чтобы вычислить вариацию по P , воспользуемся представлением (10). Пусть P _E ( u ) = P _E ( u ) + е- ю ( u ). Раскладывая выражение F ( P _E , ц ) в ряд Тейлора по переменной е , получим

F ( Р е , ц ) = F ( P , ц ) + J( V v p ( u , P ( u ) ) -

0                         (12)

• -V _v ц ( P ( u )), е to ( u )^ G ( u ) E ₀( u ) d u + o ( e ) , где угловые скобки обозначают скалярное произведение, а V _v ц ( P ( u )) и V _v p ( u , P ( u )) обозначают градиенты функций ц ( v ) и p ( u , v ) по переменной v = ( v 1 , v ₂), в которых после вычисления полагается v = P ( u ). С учётом (12), вариация по P записывается в виде

• 5 p F ( P , ц ) = eJ^V v p ( u , P ( u ) ) -

• 0                               (13)

• -VvЦ(P(u)), to (u)} G(u)E0(u) du,

3.    Связь вариационной задачи с задачей расчёта функции эйконала

где градиент функции стоимости вычисляется из формулы (6) как

V v p ( u , P ( u ) ) =

- ( u - P ( u ) ) + [ f ( P ( u ) ) - g ( u ) ]V v f ( P ( u ) ) (14) p ( u , P ( u ) )                    ■

Предположим, что для пары (P, ц) обе первых вариации равны нулю

5 p F ( P , ц ) = 0, 5 ц F ( P ц ) = °.

Поскольку в (11) а >0, а n ( v ) - произвольная функция, то из второго уравнения в (15) сразу следует условие сохранения энергии (5b). Из первого уравнения системы (15) и уравнений (13), (14) следует следующее уравнение:

• ■ P ( u ) - u + V v f ( P ( u ) ) ( f ( P ( u )) - g ( u ) ) p ^{( p (} u ⁾, u )

  -V _v ц ( P ( u )) ] E o ( u ) G ( u ) = 0.

Сделаем в последнем уравнении замену P (u) = v и, с учётом условия E0(u) ■ G(u) > 0, получим v - P-1( v) + p( v, P-1(v))

+V f ( v ) ■

f ( v ) - g ( P ^{- 1}( v )) p ( v , P ^{- 1}( v ) )

= Vp ( v ).

Полученное уравнение (16) в точности соответствует условию интегрируемости отображения P-1, приведённому в уравнении (2b). При этом в качестве функции эйконала на второй поверхности ^(v) берётся функция ц(v), обеспечивающая выполнение условия (16). В силу симметричности задачи относительно поверхностей S и W, условие интегрируемости верно и для «прямого» отображения P. Интегрируемость P, очевидно, влечёт равенство нулю первой вариации функционала. Итак, нами доказана следующая теорема.

Теорема . Отображение P : 0^0 является интегрируемым тогда и только тогда, когда существует функция ц ( v ) на 0 , такая, что пара ( P , ц ) является критической точкой функционала (9). При этом ц ( v ) является функцией эйконала обратного отображения.

Из данной теоремы следует, что не только условный минимум или максимум исходного функционала (7) даёт интегрируемое лучевое соответствие, но и любой локальный экстремум или критическая точка этого функционала.

Отметим, что в статье [1] для нахождения функции эйконала используется частный случай вышеприведённой теоремы, когда поверхность S является плоскостью z = 0, а W - плоскостью z = f

4.    Градиентный метод

В данном параграфе мы опишем численный метод, позволяющий рассчитать функцию эйконала из условия формирования заданного распределения ос- вещённости. Согласно формулам (11), (13) градиент функционала (9) имеет вид:

V ц F ( P , ц ) = E ( v ) ■ F ( v ) -- E 0 ( P ^{- 1} ( v ) ) G ( P ^{- 1} ( v ) ) J p -1 ( v ),

V p F ( P , ц ) =

_" P ( u ) - u + V v f ( P ( u ) ) ( f ( P ( u )) - g ( u ) )

P ( ^P ( u ), u )

-

(17a)

(17b)

-V v Ц ( P ( u )) ] E 0 ( u ) G ( u ).

Полученный градиент функционала позволяет найти локальный минимум функционала (9) методом градиентного спуска. Пусть у нас есть некоторое начальное приближение (P0, ц0) . Чтобы получить новое приближение, нужно вычесть из него градиент функционала, вычисленный на нём. Другими словами, n-е приближение вычисляется по (n-1)-му по следующей формуле ц n (v) = ц n -1( v) - At ■ Vц F (P n-1 (u), ц n-1 (v)), Pn (u) = Pn-1 (u) - At ■ V PF (Pn-1 (u), цn-1 (v)),

где A t - шаг градиентного спуска. В точке минимума, найденной градиентным методом (18), функция ц ( v ) соответствует функции эйконала на второй поверхности. Соответственно функция эйконала на первой поверхности может быть вычислена по формуле Ф ( u ) = ц ( P ( u ))- p ( u , P ( u )).

Заключение

Рассмотрена задача расчёта функции эйконала светового поля, заданной на некоторой поверхности, из условия формирования заданного распределения освещённости на некоторой другой заданной поверхности. Показано, что данная задача может быть сформулирована как задача Монжа - Канторовича о перемещении масс. При этом доказано, что функция стоимости в задаче о перемещении масс соответствует расстоянию между точкой исходной поверхности, на которой задана функция эйконала, и точкой поверхности, на которой требуется сформировать заданное распределение освещённости. Доказательство основано на вычислении первой вариации функционала «стоимости», описывающего задачу о перемещении масс. Установленные вид первой вариации и градиента функционала стоимости позволяют использовать для расчёта функции эйконала, формирующей заданное распределение освещённости на заданной поверхности, методы градиентного спуска.

Работа выполнена при поддержке гранта РНФ 1819-00326 (формулировка задачи расчёта функции эйконала как задачи Монжа - Канторовича о перемещении масс и получение функции стоимости) и Федерального агентства научных организаций (соглашение № 007-ГЗ/Ч3363/26) (градиентный метод расчёта функции эйконала).