Вариационно-разностное решение задач деформирования и потери устойчивости упругопластических оболочек вращения с упругим заполнителем при комбинированных квазистатических и динамических осесимметричных нагружениях

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2024PNRPU MECHANICS BULLETIN

Многие объекты авиа-, ракето-, машиностроения, химической промышленности и нефтяной отрасли содержат в качестве элементов составные осесимметричные оболочки с заполнителем. В некоторых режимах работы несущие слои таких элементов должны выдерживать не только статические, но и динамические нагружения. При превышении критических уровней нагрузок происходит потеря несущей способности конструкции из-за выпучивания оболочек. Для понижения массы оболочечных конструкций и повышения их устойчивости, а также для устранения неосесимметричных форм потери устойчивости применяется легкий (упругий) заполнитель [1; 2]. К настоящему времени весьма тщательно проработаны аналитические и численные методы описания процесса выпучивания упругих тонкостенных оболочек вращения. Исследование процессов деформирования и выпучивания упругопластических оболочек с заполнителем с переходом из осесимметричных форм в неосесимметричные возможно на основе известных методик, реализованных в вычислительных пакетах программ, путем численного моделирования только в трехмерной постановке. Время расчета такой задачи с применением вычислительных пакетов, в которых реализована явная схема интегрирования по времени, будет велико, поскольку шаг численного интегрирования определяется толщиной оболочки (т.е. малой величиной). В коммерческом программном обеспечении решение задач кручения осесимметричных тел возможно только в трехмерной постановке. Для длинных оболочек при больших углах вращения может происходить потеря точности из-за применения для учета вращения как жесткого целого производной Яуманна.

В работах [3–8] проведен анализ классической задачи о поперечной устойчивости тонкого стержня под действием осевой нагрузки при различных способах приложения нагрузки и закрепления концов. Показано, что при динамическом нагружении продольной нагрузкой генерируется пакет неустойчивых форм. Верхний номер форм зависит от скорости приложения нагрузки. Скорость оказывает влияние на форму потери устойчивости, а не на критическую нагрузку. Реализуется не минимальная и не максимальная форма потери устойчивости, возможная для данной нагрузки, а та, номер которой примерно равен 2/3 от максимальной [4]. Образование высших форм потери устойчивости стержня и круговой цилиндрической оболочки при динамическом приложении нагрузки было обнаружено экспериментально при осевом динамическом сжатии стержня [4], обжатии трубы при имплозии и внешнем давлении [4; 9–11], потере устойчивости конической оболочки при внешнем давлении [12].

В [13] рассматриваются вопросы по определению напряженно-деформированного состояния и устойчивости тонкостенных оболочек с упругим заполнителем, приводится обзор исследований. Поведение упругого заполнителя моделируют в рамках механики сплошной среды с применением уравнений теории упругости [13–18] или применяют упрощенные модели, например, упругое основание с одним или двумя коэффициентами постели (основание Винклера или Пастернака) [13; 19–27].

В настоящей статье представлены постановка и методика численного решения нелинейных задач осесимметричного деформирования и потери устойчивости упругопластических оболочек вращения с упругим заполнителем при комбинированных осесимметричных нагружениях и кручении. Задачи формулируются в динамической постановке, что дает возможность описать большие докритические формоизменения упругопластических оболочек и переход оболочки к новой, изогнутой форме равновесия. Моделирование поведения оболочки основывается на гипотезах теории непологих оболочек типа Тимошенко с геометрическими нелинейностями и теории пластического течения с нелинейным изотропным упрочнением. Заполнитель полагается упругим массивным телом. Данный подход является развитием методик численного решения нелинейных задач осесимметричного деформирования и неосесимметричного выпучивания пустотелых упругопластических оболочек вращения при комбинированных осесимметричных нагружениях и кручении [28–30], контактного взаимодействия упругопластической оболочки вращения с упругим заполнителем, моделируемым основанием Винклера [31], обобщенных осесимметричных задач с кручением для массивных тел [32; 33], контактного взаимодействия упругопластических элементов конструкций в плоской или осесимметричной постановке [34–36]. Разработанные методики были реализованы в рамках вычислительного комплекса «Динамика-2».

1.    Кинематические и физические соотношения для оболочки

Задача упругопластического деформирования и выпучивания оболочек вращения при комбинированных статических и динамических осесимметричных нагружениях с кручением формулируется в двумерной (плоской или обобщенной осесимметричной) постановке исходя из гипотез теории оболочек типа Тимошенко [29–31]. Определяющие соотношения записываются в цилиндрической системе эйлеровых координат OrzР, Oz - ось вращения. На рис. 1 показаны местная (s, ^ Р) и общая (r, z, Р) системы координат.

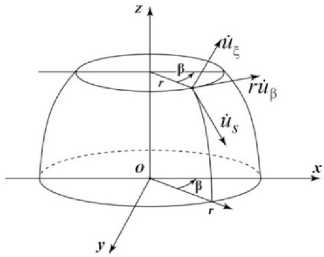
Рис. 1. Общая и местная системы координат

Fig. 1. General and local coordinate systems

Для каждого оболочечного элемента вводится местная лагранжева система координат Os ^ , связанная с общей соотношениями ds = у z dr - у _rdz , d ^ = у r dr + у z dz , где s – длина дуги меридиана оболочечного элемента; ^ - координатная линия, нормальная к срединной поверхности; Р - угловая координата; у _z = r_s , у _r = - z _s -направляющие косинусы нормали к срединной поверхности.

Оболочечные элементы полагаются тонкими, изменением метрики по толщине пренебрегаем, деформации поперечного сдвига и изгиба малы по сравнению с деформациями срединной поверхности, кинематические соотношения формулируются в скоростях и строятся в метрике текущего состояния. Распределение компонент скоростей перемещений по толщине оболочки записывается в виде:

пи u1s ( s, ^ P, t ) = us ( s, P, t ) + ^Фs ( s, P, t )

up (s, ^ P, t) = rule (s’ P’t) + ^Pp (s, P, t) ’ здесь uis (s, в, t) и u^ (s’в, t) - скорости перемещений срединной поверхности в направлении касательной и нормали, lip (s’ в, t) - скорость угла поворота по окружной координате p , фs (s, p, t) и фp( s, p, t) - угловые скорости поворота поперечных сечений в плоскости меридионального сечения и в плоскости O^р .

Распределение компонент скоростей деформаций (симметричной части градиента скорости перемещений) eу по толщине оболочки представляется в виде суммы скоростей деформаций срединной поверхности Ёу и изгиба Xij ■ Компоненты скоростей деформаций Ej , Xij и скорость вращения элемента 6)sв записываются в местном базисе s^р :

e ij = ^е ij + & ij , Ч = ^е i ^ + Z i ^ ( i , ^j = s , ^р ), ^ = ^е _й ^,

ε ss

д i_s     1 .

=+i, E, д s    Rs ^ ’ 1

■

^{д и} р i t _s д r    1 .

=11 i , ^рр др r д s R ^

е„ = 1 ^f r ^ u U 1 « us. ^{s р} 2 ( д s r др

-

.. ^{д r} I ^рд s J ’

е

1 f д i _t 's^ = t|

2 1 д s

-

1 .

u R s

, е

1 f 1 д i ^

-

'^K 2 ( r др R

1 . 1 u R

■

^{X ss}     д s ’

1 f д< рр . д r 1 ^% рр="13ц Ф s T I ’ r ( др д s )

». = 1 ^{f дф} . 1 ^{Ф sP} 2 ( д s r др

-

Ф р d r ) r д s ) ’

tt

⁶ ij = J D J ⁶ ij dt . i . ^j = ^s . ^р . ⁶ s ^ = J< 7 s ^ dt          ⁽⁴⁾

0                                    0

Здесь D J - производная Яуманна, которая учитывает поворот элемента оболочки за счет сдвиговой деформации как квазижесткого целого относительно нормали к ее срединной поверхности при кручении. Местная сопутствующая система координат Os ^ определяется формоизменениями оболочки без учета сдвиговых деформаций кручения, то есть она является лагранжевой только для осесимметричной деформации. Заметим, что деформации сдвига при кручении тонких оболочек ограничены из соображений устойчивости осесимметричного процесса деформирования. Поэтому введение производной Яуманна для учета квазижесткого вращения при кручении вполне обоснованно при использовании явной схемы интегрирования с малыми шагами по времени [29]. В итоге существенно упрощается запись основных уравнений обобщенной осесимметричной задачи с кручением, так как за базовую берется лагранжева система координат осесимметричной задачи.

Учет упругопластических свойств материала оболочки осуществляется в рамках теории течения с нелинейным изотропным упрочнением:

■              6‘ ej = ^nij,nij = / / / ,6у6у = 6t (ж),6‘ = 6ij ~6^ij , σijσij

⁶ = ( ⁶ ss ⁺⁶рр ) ³-^U = ^|J -xU^dt .        ⁽⁵⁾

здесь 6 _T ( ж ) - радиус поверхности текучести; ж - параметр Одквиста, 5 ij - символ Кронекера; параметр X определяется из условия прохождения мгновенной поверхности текучести через конец вектора догрузки.

Усилия N ij , моменты M ij , масса N _р и момент инерции M _р определяются по формулам:

1 ...

1 .

x s ^ = ^ ф s ^, X p^ = ^ Ф р ^{, b} s p =

■

■

■

-

— ri„ ..

2 ^р ’ ^s

Выражения для компонент скоростей деформаций через компоненты скоростей перемещений в общем базисе rz р получаются из (2) путем подстановки выражений i_s = i r V _z - i_z V _r , u ^ = i_r V _r + i_z V _z , они приведены в [29].

Компоненты тензора скоростей деформаций e ij можно представить в виде суммы упругой e ij и пластической e p составляющих. Предполагается, что упругие деформации малы, а пластические деформации могут быть большими. Компонента тензора напряжений Коши, нормальная к срединной поверхности оболочки, принимается равной нулю. Из условия плоского напряженного состояния и обобщенного закона Гука определяется компонента e ,, :

^e j = ^e e ^{+ e} ip , e p = ⁰ ( i , ^j = ^s , ^р ^           ⁽³⁾

6 «=о %=-^E_T ( e ss + e , ) •

Ц ^{- 1}

Компоненты тензоров скоростей напряжений 6 _у и напряжений Коши 6 _у в местном базисе s ^р записываются в виде:

N , ( р ) = _[6 у ( р ) d ^ , м ,( р ) = _[6 у ( р ) ^ d ^ , i, j = s , р , ^

-h/2

Nр(р)=<[рd^, Mр(р)^Р^2d^-(6)

-h/2

• ⁶ ss   ,    2 ⁽ e ss ⁺ M e рр ) . ⁶ рр          2 ⁽ e р^+Ц e ss ) .

• 1    - Ц                   1 - ц

2. Кинематические и физические соотношения для заполнителя

E e E e

^{6 s р} = 1 + ц e^{s р} ’ ^{6 s} ^ = 1 + ц e^s ^ ’ ⁶^^ = ^{6 р} ^ = 0.

D J ⁶ у = ⁶ jk <» ki ^{+ 6} ik <» kj . i . ^j . ^k = ^s . ^р .

Определяющая система уравнений двумерных задач в плоской или обобщенной осесимметричной (с кручением) постановке записывается в декартовой или цилиндрической системе эйлеровых координат r , в, z ( Oz -ось вращения) в текущей лагранжевой постановке [32]. В силу осевой симметрии или плоской постановки все

искомые функции зависят от радиальной и осевой координат и не зависят от окружной.

Кинематические соотношения формулируются в скоростях и строятся в метрике текущего состояния, что позволяет учитывать большие формоизменения. Компоненты тензоров скоростей деформаций (симметричной части градиента скорости перемещений) e j и скоростей вращения кг- при учете равенства u t e = r 6 (0 - угол закручивания по окружной координате β ) имеют вид:

е = и . е™ = u_r ^-1, e =u rr     r , r ^, ββ r ^, zzz , z ^,

1    11

^e zr = 2 ( u z , r ^{+ u} r , z ) , ^e r e = 2 r ⁰ , r , ^e e z = 2 r ⁰ , z ,      ⁽⁷⁾

• ⁰ zr = 2 ( u z , r ^- u r,z ) , ⁰ r e =- 2 ( r ⁶ , r ^{+ 20} ) , ° ₽ z = 2 r ⁶ , z .

Точка над переменной означает частную производную по времени, а символ после запятой – частную производную по соответствующей координате. В силу осевой симметрии в выражениях для компонент тензоров скоростей вращения 0_у (последние три равенства в (7) полный угол поворота относительно оси Oz не учитывается.

Упругопластические свойства материалов описываются теорией течения с нелинейным изотропным упрочнением. Связь между компонентами девиатора скоростей напряжений ° j = ° j + P5_у и упругими составляющими компонент девиатора скоростей деформаций '

( e ij ) = e j - e S j /3 - e p осуществляется на основе обобщенного закона Гука в метрике текущего состояния:

D J ° 8 = ² G ( ^еу ) ^, D J ° j = ° j ^{- 0} k ° к ^{- 0} jk ° jk ,

P = - Ke ^e , P = -°„ /3, e = е е , e p = 0 -     (8)

где D_J – производная Яуманна, описывающая поворот частицы среды как жесткого целого; K , G – модули объемного сжатия и сдвига; P – давление; δ _j – символ Кронекера. Скорости пластических деформаций определяются ассоциированным законом течения:

• = ^°j/> °jj°jj = 3 °²($) , °j = °j ($) .

• $=31 j 7^e-P^ePdt,                (9)

3.    Уравнения движения оболочки с заполнителем с учетом контактного взаимодействия

где ° = ° ( $ ) - зависимость интенсивности напряжений от параметра Одквиста æ при монотонном нагружении (истинная диаграмма деформирования материала).

Вариационные уравнения движения элементов конструкции (как оболочек, так и заполнителя) редуцируются из трехмерного уравнения баланса виртуальных мощностей работы механики сплошных сред:

k Г

^ jjj ° ° ^ e j dV ⁺ jjj P u^ udV - jj P‘ 5 u* ds - jj Q^u ds = 0'⁽¹⁰⁾

k = 1

pk                Sqk

Здесь V_k – объем, занимаемый k -м элементом конструкции (исследуемая область); K – количество элементов конструкций; S_pk – зона действия внешнего давления; S_qk - поверхность контакта; u_j , u - компоненты векторов скорости перемещения и ускорения в общей системе координат; G _y и e j - компоненты тензоров напряжений Коши и скорости деформаций (симметричной части градиента скорости перемещений); р - плотность; q – контактное давление; p – распределенная нагрузка; 5 e j , 5 u - вариации e j , й (на поверхности с заданными кинематическими граничными условиями 5 й _t = 0 ); j , j = r , p , z , точка над символом означает частную производную по времени t ; по повторяющимся индексам ведется суммирование.

Вариационные уравнения движения оболочки выводятся из общего уравнения динамики (10) с учетом принятых гипотез теории оболочек (1)–(6):

L j{(NsSVr + Nss Vz ) 5ur,s + (NsSVz - Nss Vr ) 5uz,s + vrNsP5г*р,s + 0

^{+ M}ss ⁵г* ф , s ⁺ [ ^{vr - 1 N} PP ^{+ N} P ( ^ur ^- vru » ² ) ^- Pr ^- 4 r ] ^5г* r ⁺

⁺ ( N р ^uz ^- p_z ^- Q z ) ⁵ u z ⁺ v ( ^{r 2} N р u p ^- P e ^- q p ) ⁵ u p ⁺

⁺ ( ^Ns 5 ⁺ v ^{r 1 M} PP ^V z ^{+ M} р “ ф ) ^{5 u} Ф ⁺

+ v ( N p5 - M s _pv z + M _P “ e ) 5 u p } rds -

• -[ r ( P_r 5 u_r + P_z 5 u_z + V p _e5 u _e + T_s 5 U _ф ) ] s 0L = 0. (11)

Здесь v - параметр симметрии ( v = 0 - плоская деформация, v = 1 - обобщенная осесимметричная деформация с кручением); us (s, t), u^(s, t) - скорости перемещений срединной поверхности в направлении касательной и нормали; uф( s, t) - угловая скорость поворота поперечных сечений в плоскости меридионального сечения; uр (s, t) - угловая скорость поворота относительно оси вращения; q – контактное давление; p – распределенная нагрузка; N j , M j – внутренние усилия и мо- менты; Mp , Jp - масса и момент инерции; Pi и Ts -внешние усилия и изгибающий момент.

Вариационные уравнения движения сплошной среды (заполнителя) выводятся из общего уравнения динамики (11) с учетом соотношений Коши и условий плоского деформированного состояния или обобщенной осесимметричной деформации с кручением (7)-(9):

ее I эз v_r ( эз v_r эз v , JJ j° ^rr d r ⁺° rz [ "dT⁺”d 7 n L

I °rr   °вв 5 • GH •I , v -----—3 v + —z 3 v+ rz

I rr

d3> , L 930 , „ 930)    , _. ,      2 . , J

+ ° zz ,— + v | О _r „ —— + G„ —— I + p ( w_r 3 v_r + v w _e r 30 + w z 3 v z ) ) d n -9 z       I       9 r          9 z I '                                   ’ I

- J ( Pr ^{3 v} r ^{+ v} P e ^r 2^{30 +} P z ^{3 v} z ) ^dS -

S p

J ( q r 3 v r + v q _p r ² 30 + q_z 3 v_z ) dS = 0.

S q

Здесь Q - площадь, занимаемая меридиональным сечением заполнителя; Sp - зона действия внешнего давления; S„ - зона контактного взаимодействия; и>,, и -q                       ii компоненты векторов скорости перемещения и ускорения в общей системе координат; сц и eij - компоненты тензоров напряжений Коши и скорости деформаций (симметричной части градиента скорости перемещений); p - плотность; qi - контактное давление; pi - распределенная нагрузка; 3eij, 3Ui - вариации eij, Ui (на поверхности с заданными кинематическими граничными условиями 3Ui = 0 ); v - параметр симметрии (v = 0 -плоская деформация, v = 1 - обобщенная осесимметричная деформация с кручением), функции va = rv Ua (а = r, z), и 0 = vr 1 Up введены в задаче с осевой симметрией для устранения особенности численного решения на оси вращения.

Определяющая система уравнений (1)-(12) дополняется начальными и кинематическими граничными условиями. Для ее решения применяется вариационно-разностный метод и явная схема интегрирования по времени типа «крест».

Скорости перемещений и перемещения узлов разностной сетки заполнителя и срединной поверхности оболочки определяются по рекуррентным соотношениям:

Взаимодействие элементов конструкции (оболочки и заполнителя) обеспечивается дополнительными кинематическими и статическими условиями на контактных поверхностях. Полагается, что у массивных тел контактными границами являются части контура, а у оболочек -части срединной поверхности. Компоненты контактного давления q _а( а = r , z , р ) , положение и конфигурация контактных поверхностей в общем случае заранее неизвестны и определяются в ходе решения задачи.

Моделирование контактного взаимодействия оболочки и заполнителя основано на условии непроникания по нормали и проскальзывания по касательной [34; 35; 37]. На участке контакта вводится местный базис ( s , ^ , в ) . Здесь s - направление касательной, ^ - нормали к поверхности, в - окружная координата (совпадает с окружной координатой общего базиса в цилиндрической системе координат). Усилие по нормали определяется из условия непроникания, а касательные усилия полагаются равными нулю:

u '^ = U "^ Г 0, q ^ >  0 q ^ =^{- q} ^ ^ ^ L ^q ^ , ^q ^ < ⁰

u > 'а * ¹>а, q 'а = q а= ^{0 а} = s ,^в . (14)

Функции со штрихом относятся к контактирующей поверхности оболочки, а с двумя штрихами - заполнителя. Условия непроникания (14) выполняются только в активной фазе контактного взаимодействия. При нарушении контакта они заменяются условиями на свободной поверхности.

Для вычисления контактных давлений вариационное уравнение движения контактных границ записывается в местном базисе (s, ^, в). Сначала по известному на момент времени t = tk распределению параметров напряженно-деформированного состояния для узлов разностной сетки обеих контактных границ находятся скорости „ _               ■ k+1/2 „ _              ..к+1 „          „ „ перемещений и^   и перемещения и^ по нормали по рекуррентным соотношениям (13) (а = ^) без учета контактного взаимодействия (q^ = 0). По перехлесту сеток определяется зона контакта. Если перехлест сеток для узлов отсутствует, то полученное решение является для них истинным. В противном случае определяется контактное давление, исходя из условий (13) и (14):

А , k + 1/2

• k + 1/2      -k - 1/2 . k^k . k .    k \ ^А t

U_a   = ^Ua + Ф а + q ^ + Pa ---Г"

а       а у а а а а у ф k

,

а ^{k + 1 q} ^

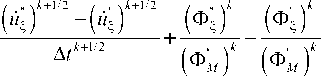
k

k + 1       k , - к + 1/2 ж Л + 1

^u а   = ^u а ^{+ u} а  ^А t  ,

где для оболочки а = r , z , ф , в , для массивного тела а = r , z , в , Ф а , Ф ^ - обобщенные узловые силы и масса или момент инерции.

1        1

+ .

^Ф M ^Ф M _

Нормальные контактные давления, вычисленные в местном базисе по формуле (15), перепроецируются из местного базиса в общий. Затем осуществляется расчет

k + 1/2                           » + + 1

скоростей перемещений иa   и перемещений иa обо лочки (a = r,z,ф,в) и заполнителя (a = r,z,в) по стандартной вычислительной схеме (13) с учетом контактных давлений.

Разработанный подход позволяет моделировать нелинейное докритическое деформирование оболочек вращения с упругим заполнителем, определять предельные нагрузки в широком диапазоне скоростей нагружения с учетом геометрических несовершенств формы, исследовать процессы потери устойчивости по осесимметричным и неосесимметричным формам при динамических и квазистатических комбинированных нагружениях в условиях плоской и осесимметричной деформации.

4.    Результаты численного моделирования

С применением разработанной методики исследована задача деформирования и потери устойчивости стальных цилиндрических оболочек с упругим заполнителем при равномерном внешнем давлении. Толщина оболочки h 0 = 1 мм, радиус R 0 = 14,5 мм. Материал оболочки – сталь Х18Н10Т с механическими характеристиками: модуль упругости E = 2,1 - 10 5 МПа, коэффициент Пуассона Ц = 0,3, плотность р = 7,8 - 10³ кг/м³, диаграмма деформирования материала приведена в [2].

Результаты численного исследования сопоставлялись с расчетами, выполненными с применением двух других численных подходов.

Первый подход основан на полномасштабном моделировании процесса деформирования и оболочки и заполнителя в рамках механики сплошных сред [32; 34; 35]. Для описания формоизменения элемента сплошной среды кинематические соотношения формулируются в скоростях и строятся в метрике текущего состояния (7). Упругопластические свойства материала оболочки описываются теорией течения с нелинейным изотропным упрочнением (8), (9). Материал заполнителя полагается линейно упругим. Вариационные уравнения движения оболочки и заполнителя (12) следуют из уравнения баланса виртуальных мощностей (12). Контактные усилия определяются в ходе решения задачи исходя из условий непроникания по нормали и свободного проскальзывания вдоль касательной. Условия непроникания выполняются только в активной фазе контактного взаимодействия, при нарушении контакта они заменяются условиями на свободной поверхности (14), (15).

Во втором подходе применяется упрощенная постановка, в которой деформирование оболочки моделируется согласно гипотезам теории непологих оболочек типа Тимошенко с учетом геометрических нелинейностей [28–31], а заполнитель – гипотезе основания Винклера [31; 37]. Кинематические соотношения записываются в скоростях и формулируются в метрике актуального состояния (1), (2). Физические соотношения материала оболочки учитываются теорией течения с нелинейным изотропным упрочнением (3), (4). Уравнения динамики оболочки (11) выводятся из уравнения баланса виртуальных мощностей работы (10). Контактное взаимодействие оболочки и деформируемого заполнителя моделируется из условий непроникания по нормали и свободного проскальзывания вдоль касательной (14). Полагается, что контактное давление в области взаимодействия оболочки с заполнителем пропорционально прогибу оболочки с коэффициентом постели γ , т.е. принимается гипотеза Винклера [31; 37].

Представленную в данной статье методику (1)–(15) для краткости изложения будем называть третьим подходом.

Полагалось, что оболочка и заполнитель находятся в условиях плоского деформированного состояния. Расчетная область представляет собой поперечное сечение оболочки с заполнителем. В случае моделирования заполнителя основанием Винклера (второй подход) задавались значения коэффициента постели: у = 3000,5000, 7000 и 10 000 МПа/м. Для расчетов по второму и третьему подходу (заполнитель – сплошная среда) для каждого коэффициента постели задавались: плотность р = 40 кг/м³, коэффициент Пуассона ц = 0,3, три варианта начальной толщины заполнителя H ₀ = 3, 8 и 13 мм. Для каждой толщины заполнителя вычислялся модуль упругости согласно формуле у = E / ( H ₀ ( 1 - 2 v ² ) ) [19].

Внешнее давление монотонно возрастает по линейному закону от времени: p = p ₀ t . В расчетах задавалось три варианта параметра скорости нагружения p ₀ : 50; 5000 и 50 000 МПа/с. Во втором и третьем подходах на внутренней поверхности заполнителя задавался запрет перемещений по нормали. Начальные несовершенства оболочки (отклонение поперечного сечения от круглой формы) моделировались начальной погибью срединной поверхности с относительной амплитудой A = 1 - 10 ^{- 5}: A R 0 = Ah ₀cos и в , n = 2,3, ^ ,0 < в <  2 п .

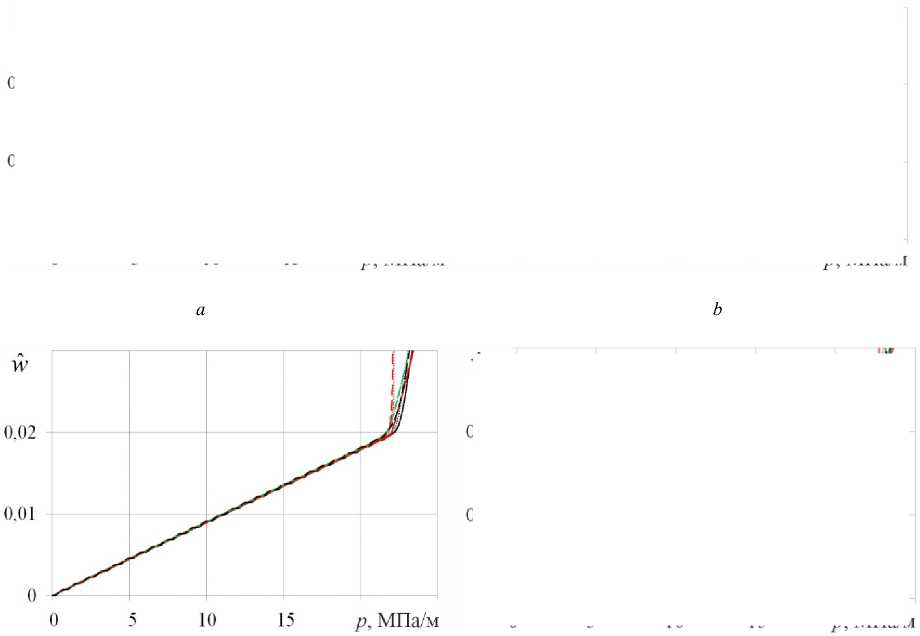
На рис. 2 приведены расчетные зависимости относительного среднего прогиба w ˆ от внешнего давления p . Относительный средний прогиб оболочки определялся по формуле:

L w=L Е(u 4’ i=1

w

W =--, h0

где w – средний прогиб, L – количество узлов разностной сетки в окружном направлении, где ( и ^ ) . - прогиб (перемещение по нормали) i -го узла расчетной сетки, покрывающей срединную линию оболочки.

В качестве критерия потери устойчивости оболочки примем резкий рост относительного среднего прогиба wˆ . Первый докритический безмоментный этап деформирования оболочки характеризуется линейным ростом относительного среднего прогиба wˆ . Второй закритический этап деформирования проявляется резким ростом относительного среднего прогиба wˆ , так что графики зависимостей среднего прогиба wˆ от давления p близки к двухзвенным ломаным (см. рис. 2). Величину внеш*

него давления p , при которой происходит излом кривых, будем называть предельным давлением. Критическое давление, которое определяется как собственное значение, и предельное давление могут различаться при динамическом нагружении.

В первом [31] и третьем подходах расхождение величин предельного давления p ^* для каждого фиксированного значения коэффициента постели γ и различных начальных толщинах заполнителя H ₀ h ₀ = 3,13 не превышает 1 %, поэтому для расчетов с этими подходами все графики приводятся для расчетов с H ₀ = 8 мм.

Из рис. (2, a ) видно, что для пустотелой оболочки при динамическом нагружении величина предельного давления р ^* увеличилась на 12 % по сравнению с квази-статическим. C увеличением жесткости заполнителя γ уменьшается влияние скорости нагружения р 0 на предельное давление р ^* (см. рис. 2, b–c ). На рис. 3 приведены эти же зависимости при квазистатическом (см. рис. 2, a ) и динамическом ( р 0 = 5000 МПа/с) (см. рис. 2, b ) нагружениях. При квазистатическом нагружении жесткость заполнителя существенно влияет на предельное давление р ^*. Разброс значений р ^* составляет около 20 % (см. рис. 3, a ). При динамическом нагружении предельные давления р ^* практически совпадают (см. рис. 3, b ). Увеличение жесткости заполнителя, так же, как и увеличение скорости нагружения приводят к увеличению предельного давления р ^*, поскольку и заполнитель, и силы инерции оказывают поддерживающий эффект.

d

c

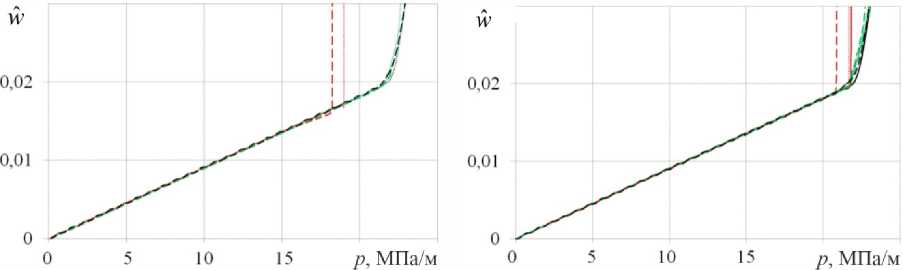
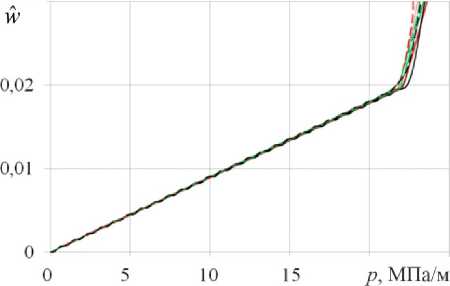
Рис. 2. Зависимости относительного среднего прогиба от давления: коэффициент постели: γ = 0 ( a ), 3000 ( b ), 7000 ( c ) и 10 000 ( d ) МПа/м; первый подход – пунктирные линии, второй подход – точки, третий подход – сплошные линии; параметр скорости нагружения р 0 : 50 (красные кривые); 5000 (зеленые кривые) и 50 000 (черные кривые) МПа/с

Fig. 2. Dependence of the relative average deflection on pressure: bed coefficient: γ = 0 ( a ), 3000 ( b ), 7000 ( c ) and 10 000 ( d ); first approach is shown with dotted lines, second approach is shown in dots, third approach is shown in solid lines; loading speed parameter р 0 : 50 (red curves); 5,000 (green curves) and 50,000 (black curves) MPa/s

1 : I 1 1 ;             1 1 !             I H    l	i           w                                                       ' 4                                                              1
	0.01

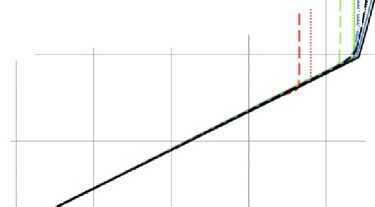
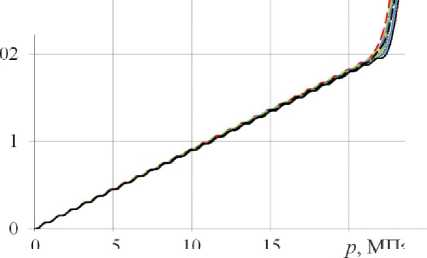
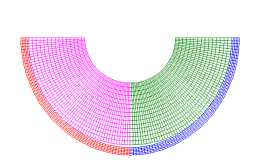
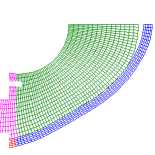
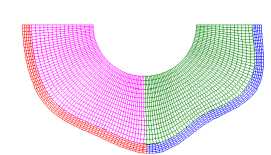
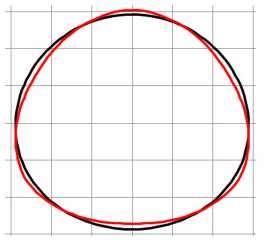
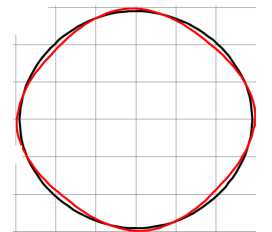
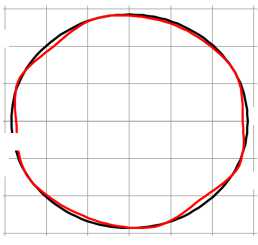
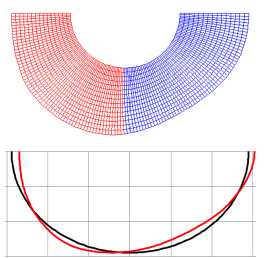
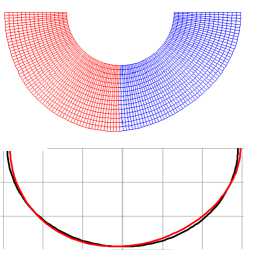
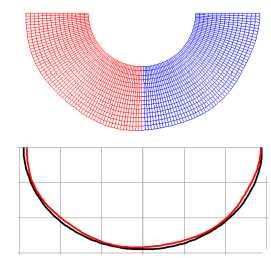
С увеличением скорости нагружения и жесткости упругого заполнителя наблюдается рост номеров преобладающих форм потери устойчивости, имеющих наибольшую скорость роста. Пустотелые оболочки в проведенных расчетах теряли устойчивость по второй форме. На рис. 4 приведены формы потери устойчивости оболочки, полученные в расчетах по трем подходам, коэффициент постели γ = 3000. Для первого подхода приведены расчетные сетки оболочки и заполнителя после потери устойчивости ( а–с ). Для второго подхода красными линиями приведены срединные линии оболочек после потери устойчивости, черными – ее начальная форма ( d–f ). Для третьего подхода приведена расчетная сетка заполнителя и срединные линии оболочек ( g–i ). Потеря устойчивости оболочки с заполнителем (коэффициент постели γ = 3000) в расчетах с параметром скорости нагружения p 0 = 50 МПа/с происходит по второй или третьей форме ( a , d , g ), p 0 = 5000 МПа/с – по третьей ( b , e , h ) и p 0 = 5000 МПа/с ( c , f , j ) – по смешанной форме более высокого порядка.

Заключение

Представлен подход к описанию контактного взаимодействия упругопластических оболочек вращения с упругим заполнителем при статических и динамических осесимметричных нагружениях с кручением. Приводится сопоставление результатов численного решения задачи о нагружении равномерным внешним давлением упругопластических пустотелых и заполненных упругой