Вариационные методы как наиболее эффективный механизм при моделировании взаимосвязанных физических полей в сплошных средах. I. Краткий обзор теории

ВВЕДЕНИЕ                      Вариационные методы, первоначально возник-

В теории научного приборостроения часто приходится сталкиваться с перекрестным взаимодействием физических полей различной природы (гидродинамических, электромагнитных), различных явлений переноса и т. д., когда действие одного поля на другое порождает обратное воздействие. В случае отсутствия перекрестных взаимодействий полей или их слабого взаимодействия при построении уравнений процесса, как правило, доступно использование разнообразных методов, включая и вариационные. Однако при нетривиальных взаимодействиях полей, которые имеют место, например, для взаимопроникающих сред типа дисперсных смесей или для таких явлений, как акустика пористых сред и т. д., единственным способом построений физически разумных уравнений становится вариационный подход [1, с. 7]. В качестве примеров такого подхода можно привести теоретическое решение Рэлеем задачи Рэлея—Плато о капиллярной неустойчивости струй [2] или построение Био взаимосвязанных систем уравнений в теории акустики пористых сред [3, 4] (по этому поводу см. также работу [5], а также обзор [6]). Множество примеров применения вариационного подхода, когда он является единственно возможным, приведено, в частности, в работе [1]. Кроме того, в [1] помещена обширная библиографическая подборка публикаций по рассматриваемому вопросу.

шие в аналитической механике, развивались усилиями таких классиков науки, как Ферма, Бернулли, Мопертюи, Эйлер, Даламбер, Лагранж, Гамильтон, Пуанкаре и др. (см. сборник основополагающих пионерских работ на эту тему в работе [7]). Из длинного ряда работ, затрагивающих применение вариационных подходов к другим областям физики, сошлемся лишь на обзорную работу [8], классический трактат [9], где вводится понятие диссипативной функции, классические монографии по математической физике [10, 11]. Из узкоспециальных приложений вариационных методов отметим работы [12–14] и еще раз отметим обширный библиографический обзор в [1] по разнообразным приложениям вариационных методов в физике.

ПОСТАНОВКА ЗАДАЧИ

В настоящей работе рассматриваются особенности вариационного подхода применительно к механике сплошных сред, позволяющие достаточно просто находить уравнения движения как для консервативных, так и для диссипативных систем, что является нетривиальной задачей, при том что сам вариационный подход зачастую является безальтернативным в подобной ситуации, в том числе при перекрестном взаимодействии физических полей различной природы.

ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ

Говорят, что поведение сплошной среды известно, если известна зависимость от лагранжевых координат и времени некоторой системы величин и^к , k = 1,2,..., характеризующих состояние среды и называемых определяющими функциями [1, с. 10]. Построение любой модели сплошной среды начинается с перечисления ее определяющих функций. Так, в частности, в случае движения натянутой гибкой струны такой функцией является ее отклонение от состояния равновесия u = ^ ( x , t ) [11, с. 288], а в случае потенциального движения невязкой жидкости в линейном приближении таковым является потенциал и = ф ( x , y , z , t ) скорости жидкости v ( x , y , z , t ) , v = У ф [11, с. 294] и т. д.

Задание модели сплошной среды означает построение замкнутой системы уравнений для определяющих функций.

Приведем некоторые общеизвестные определения [1].

Вариацией 5u^k ( x , t ) функции u^k ( x , t ) называют величину

5I =— д s

dε , е=0

называемая вариацией функционала I .

В вариационных подходах обычно рассматривают интегральные функционалы вида [1, с. 14]

I ( и ) = Jл ( x i , u^k , и^к ) d n x .                     (2)

V

Здесь введено стандартное сокращение для производных функции f ( x 1 , x ² ,..., x i ,... )

f i =

a f д x i

Согласно (1), 5 ( и * ) = ( 5u^k ) . Дифференциро

вание по s функции I ( и , s ) дает [1, c. 14]

5I-J

V

1 дЛ v    дЛ

—_k 5u^k + — k д и^к      д и

, i

( 5u^k ) d n x =

у

= f ⁵ ^- 5u^k d n x + f ^4 5u^kn_l d n ^{- 1} x .

^J 5u^k            ^ V д и k      i

5u^k ( x , t ) =

д u^k ( x , t , £ ) д s

k d s = и d s .

£ = 0

Здесь

С точностью до малых (ds )2 можно написать uk (x, t, s) = uk (x, t) + 5ик (x, t).

Из определения (1) вытекает, что оператор δ обладает свойствами оператора дифференцирования:

5 (f + g) = 5(f) + 5(g),5 (f • g ) = 8 (f )• g + f • 5( g).

Если F — заданная функция u^k , то

5F =     5u^k .

д u^k

5 Л дЛ д дЛ ; 5и^к д и^к д x¹ д и^к , i

n = ( n 1 ,n ₂, n₃) — нормаль к границе д V области V . Полагая, что на д V 5и^к = 0, имеем

г

Г 5Л g k,n fl дЛ5I = J "ТГ5и d x = J TT

V 5и           V ^д и

—

д дЛ ax7     ,

, i

δu^k d ⁿx .

Условия стационарности интегрального функционала . Стационарные точки интегрального функционала (2) удовлетворяют [1, с. 15] в области V уравнениям

5 Л= о, δu^k

Вариации функционалов. Пусть I ( и ) — некоторый функционал, определенный на множестве М . Берется некоторый элемент и еМ и строится семейство процессов сравнения и ( s ) , и ( 0 ) = и , s >  0 . На каждом семействе процессов сравнения и ( s ) функционал I становится функцией s . Вводится величина

а на границе области д V краевым условиям

дЛ а

—г n = 0.

д u k i

, i

В случае отсутствия вариаций на границе 5u^k = 0 для стационарности функционала (2)

I д V достаточно условия (3).

ВАРИАЦИОННЫЕ ПРИНЦИПЫ И УРАВНЕНИЯ

Вариационные принципы

История механики и физики изобилует многочисленными попытками объяснить происходящие явления при помощи небольшого числа универсальных законов и общих принципов. Наиболее удачные попытки связаны с идеей о том, что наблюдаемые явления обладают экстремальными свойствами и искомые общие принципы носят вариационный характер [1, 7, 8 и др.]. Еще Аристотель писал, что природа "идет легчайшим путем, с наименьшими затратами". Первым к физической проблеме этот принцип применил П. Ферма в 1662 г., исследуя закон преломления света на границе двух различных по оптическим свойствам сред. При этом он принял постулат: "Природа действует наиболее легкими и доступными путями. …Свет выберет такой путь, чтобы время его прохождения оказалось минимальным". Из этого принципа немедленно следует закон Снеллиуса преломления света. В механике первым вариационный принцип сформулировал Мопертюи. Затем усилиями Эйлера, Лагранжа, Гамильтона, Остроградского, Якоби и Пуанкаре этот принцип аналитической механики для консервативных систем с конечным числом степеней свободы был доработан до современного состояния и носит в настоящее время название "принцип наименьшего действия". Интегральный функционал (2) в этом случае имеет вид t2

S = J L ( t ) d t ,                (2а)

t ₁

где S — действие; L (t) = L (q (t), q (t), t) — функция Лагранжа, равная т. н. кинетическому потенциалу L = K - П , K и П — соответственно кинетическая и потенциальная энергии системы; q и q — совокупность обобщенных координат и их производных по времени. Уравнение (3) в этом случае имеет вид дL  d дL

= 0.

5 q^k d t д с[^k

Принцип стационарного действия в форме Гамильтона утверждает, что истинная траектория механической системы является стационарной точкой функционала (2а) на множестве траекторий, выходящих в момент времени t1 из точки q1 и попадающих в момент времени t2 в точку q2 [1, с. 23]. Существует также эквивалентный ему принцип стационарного действия в форме Гамильтона—Пуанкаре, когда действие (2а) имеет вид t2

S = J ( p , q ' - H ( p , q ) ) d t ,            (2б)

t ₁

где p = ( p 1 , p ₂,... ) — импульс системы; H ( p , q ) — функция Гамильтона системы, определяемая как преобразование Лежандра функции L по скоростям [1, с. 95] и равная для консервативных систем сумме кинетической и потенциальной энергий. Стационарные точки функционалов (2а) и (2б) совпадают.

Накопленные в физике результаты показывают [1, с. 24, 33], что вариационные принципы справедливы для всех фундаментальных физических полей, а также для микроявлений, которые можно считать обратимыми. Все элементарные взаимодействия частиц, все поля (электромагнитные, гравитационное, сильные и слабые внутриядерные взаимодействия) подчиняются законам, следующим из условий стационарности некоторого действия. Более того, убеждение в справедливости этого факта стало "общим местом" настолько, что в новых ситуациях, когда закономерности изучаемого явления еще неизвестны, предлагается заранее действие, минимизацией которого находят искомые уравнения. Так был получен ряд уравнений квантовой механики, усовершенствованы уравнения теории относительности. Поэтому в настоящее время утверждается, что все известные фундаментальные физические поля удовлетворяют принципу стационарности действия [1, с. 24].

Необходимо отметить, что в основе применения вариационных принципов лежит некоторое вариационное уравнение, связанное с вариационной формулировкой первого и второго начал термодинамики. В случаях, когда применим вариационный принцип, он эквивалентен некоторому вариационному уравнению (ВУ). В общем случае вариационное уравнение неголономно (определение см. ниже) и не сводится к условию стационарности какого-либо функционала. Условия голономности вариационного уравнения будут даны ниже.

Вариационные уравнения

Исторически первым вариационным уравнением был принцип возможных перемещений ("золотое правило механики") [1, с. 28].

В современном виде его сформулировал Бернулли. Здесь приводится формулировка для системы материальных точек, подчиненных некоторым кинематическим идеальным (т. е. при отсутствии потерь) связям. Пусть xs — координата s-й точки; Fs — сила, на нее действующая; δxs — бесконечно малые перемещения, совместимые со связями. Для нахождения системы в состоянии равновесия необходимо и достаточно, чтобы суммарная работа внешних сил на возможных перемещениях была равна нулю

Z F , • 5 x , = 0. (5)

s

При отсутствии кинематических ограничений ( 5 x s = 0) уравнение (5) тривиально: F s = 0 .

Принцип Даламбера и уравнение энергии перемещений. В задачах динамики ВУ (5) будет справедливым, если к силам F _s добавить силы инерции — m_s a _s

Z ( F ^— m s a s ) • ^{5 x} s = 0. ⁽⁶⁾ s

Здесь m_s , a _s — масса и ускорение s -й частицы соответственно. ВУ (6) называется принципом Даламбера. В случае отсутствия связей из (6) следуют уравнения Ньютона.

ВУ (6) (принцип Даламбера) считают исходным постулатом механики систем с конечным числом степеней свободы.

В работе [15] было показано, что вариационное уравнение механики (6) есть уравнение энергии, записанное для возможных перемещений, которое записывается так:

5K = 5 A + 5 Q .               (7)

Здесь 5A^e = Z F _s • 5 x _s — работа внешних сил;

s

K = Z "" m ^-2 ss s 2

функция 5 Q

— кинетическая энергия системы;

определяется так:

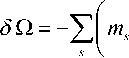
dv s δx

s

—

_s d x I m v δ ^s .

dt J

Функционал 5 Q на действительном движении обращается в нуль, поэтому на действительном движении вариационное уравнение (7) переходит в уравнение энергии

5K = 5 A .

ВУ (7) можно рассматривать как запись первого начала термодинамики (уравнения энергии) для возможных перемещений в случае систем с конечным числом степеней свободы [1, с. 30]. Отметим схожесть последнего уравнения и уравнения Лагранжа второго рода (см., например, [16, т. 2, с. 542]).

Как видно из (7), в ВУ не вошел вклад энергии, связанный с диссипацией. Это в данном случае и означает идеальность связей. Для неидеальных связей ВУ (7) содержало бы соответствующий член, учитывающий диссипацию энергии.

Вариационная формулировка первого начала термодинамики. Системы с конечным числом степеней свободы характеризуются кинетической энергией K ( q , q ) и потенциальной энергией п ( q ) , по которым строится функция Лагранжа L ( q , q ) . При переходе к сплошным средам кинетическая K и внутренняя E энергии становятся функционалами от определяющих функций. Поскольку сплошная среда описывает статистические закономерности для большого числа хаотически двигающихся частиц, возникает такая характеристика, как энтропия S , которая также является функционалом от определяющих функций [1, с. 25]. Большое значение для получения результатов по данной тематике оказали работы Дж. Гиббса по термодинамике гетерогенных систем [17], а также работы Л.И. Седова (см. библиографию в [1], под номерами [212–219]).

Предполагается, что энтропия и внутренняя энергия аддитивны по массе:

S = j ps d v ,         E = j ps d v ,

VV а кинетическая энергия по объему:

K = j zedv, V где ρ — плотность массы; dv — элемент объема области V ; s и ε — плотности энтропии и внутренней энергии на единицу массы соответственно, а κ — плотность кинетической энергии в единице объема

^K = j P l v² .

В процессе при произвольных приращениях δ (а не действительных приращениях d) уравнение первого начала термодинамики таково [1, с. 30]:

5 2 = 5A + 5 Ф + 5 Q,           (8)

где 2 — энергия системы; 5A^e — приращение работы внешних макроскопических сил; 5 Ф — приток тепла и всех остальных видов энергии; 5 Q — невязка между действительным процессом и случаем произвольного допустимого приращения (в действительном процессе 5 Q = 0).

Если функционалы 2, 5Ae, 5 Ф и 5 Q опре- делены, то уравнение (8) превращается в вариационное уравнение, выражающее первое начало термодинамики для возможных приращений определяющих функций. Функционал 5 S есть вариация функционала S. Под 5Ае понимают значения функционала dAe на значениях δuk .

Приток тепла 5 Ф на любом допустимом процессе определяется так [1, с. 31]:

5 Ф = J pT5s d v - 5 Ф ',

V где 5Ф' — некомпенсированное тепло; T — абсолютная температура. После подстановки значения 5Ф в (8) получается вариационное уравнение первого начала термодинамики

5 2 = 5A^e + J pT5s d v - 5 Ф ' + 5 Q .         (9)

V

Отметим, что при выводе (9) использовалось второе начало термодинамики [1, с. 31].

Вариационное уравнение Седова [1, 15] . В ВУ (9) не все величины можно задавать независимо. Часть задается явно, часть определяется. Вводятся следующие выражения:

5 S = J p [ 1 |v| 2 + s | d v ,

V V2

г f d5x  dv)

5 Q = p l V:5x, d v .

J V dt    dt)

Работа внешних сил A^e представляется в виде суммы работ объемных и поверхностных сил 5A^e = 5A v + 5A^e_s . Здесь приняты обозначения v = ( 4, v 2 , v 3 ) , x = ( X i , x 2 , x 3 ) . После ряда несложных преобразований ВУ (9) переписывается в следующем виде [1, с. 31]:

t ₂

5 JJ a dvdt + 5W *+ 5W = 0,       (10)

t1 V где

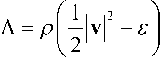
t ₂

5W = - jp55x, d v L^J •

t ₁

t ₂

+ J 5 A dt, t1

Вариационное уравнение Седова (10) имеет ме- сто для любого объема V и любого интервала времени t e[11,12 ]. Величина Л называется лагранжианом (плотностью функции Лагранжа, см., например, [11, гл. 3]). Лагранжиан Л и функционал 5W* есть задаваемые величины, а функционал δW находят из вариационного уравнения (10) [1, c. 32].

ВУ (10) имеет две отличительные черты. Во-первых, оно записано для любой части сплошной среды (это сближает его по форме с уравнением энергии (9)); во-вторых, оно содержит вклады, связанные с необратимыми процессами. Построение новых моделей в рамках вариационного подхода заключается в фиксировании набора определяющих функций и задании Л и 5W * . Вычисление δW соответствует установлению уравнений состояния.

Вариационное уравнение Лагранжа. Это уравнение используется тогда, когда V — весь объем, занятый сплошной средой, а t ₁ и t ₂ — моменты времени, в которые значения определяющих функций заданы. Тогда вариационное уравнение Седова (10) для всего объема перепишется в виде [1, с. 33]

5( I) + 5A = 0, (11) где t2

I = Jj A d v d t , A = 5W *+ 5W . (11а) t 1 V

Черта сверху говорит о принадлежности величины всему объему V .

Вариационное уравнение (11) обычно называют уравнением Лагранжа. Из уравнения Лагранжа следует замкнутая система уравнений сплошной среды, а также и краевые условия [1, с. 33].

Отметим, что вариационные уравнения первого начала термодинамики Седова и Лагранжа справедливы для обратимых и необратимых процессов.

Условимся, что при упоминании ниже вариационных уравнений вариации функционалов находятся в левой стороне уравнения, приравниваемого к нулю справа, как например в (10), (11).

В некоторых случаях (см. ниже) вариационное уравнение сводится к виду

5 ( I ) = 0 (12)

и означает, что действие имеет стационарное значение, т. е. работает вариационный принцип. Как уже отмечалось выше, вариационные принципы справедливы для всех физических полей, а также макроявлений, которые можно считать обратимыми. Что касается макроявлений, то справедливость вариационного принципа связана с тем, что осред- ненное описание процессов, в которых отсутствует "необратимая стохастичность", можно дать при помощи непосредственного осреднения микроскопического действия [1, с. 33], [11, с. 289]. Отсюда соответствующие вариационные принципы для различного рода обратимых процессов в теории сплошных сред.

Действие в физических проблемах является интегральным функционалом с лагранжианом Л , зависящим от определяющих функций (полевых переменных) u^k ( x, , t ) и конечного числа их производных по координатам и времени. Если лагранжиан Л зависит от u^k и первых производных u^k , то система уравнений вариационного типа записывается так (cм., например, [1, с. 33], [11, с. 266] и др.):

дЛ д дЛ у д дЛ duk dt дuk м dx, дuk , t ' 1, k = 1, n.    (13)

Здесь n — число определяющих функций (полевых переменных); m — пространственная раз-k duk мерность задачи; u =---; u =.

, t      at       ,1

Такую форму имеют уравнения электродинамики, гравитации, уравнения механики идеальной жидкости, теории упругости. Во всех этих теориях система (12) полностью определяется заданием только лагранжиана Л .

Важной особенностью явлений, описываемых уравнениями (13), — взаимность физических эффектов. Если рассматривается перекрестное взаимодействие между двумя полями, то действие одного поля на другое автоматически порождает обратное в некотором смысле симметричное воздействие: например, если лагранжиан Л содержит перекрестный член u _, ¹ _tu _, ² _t , то в уравнении для поля u ¹ появится сила со стороны поля 2, равная u _, ² _tt и наоборот. Поэтому во всех случаях, когда взаимодействие нетривиально, вариационный подход становится единственно пригодным для построения уравнений, описывающих такие физические процессы .

Уравнениям, которые учитывают необратимые процессы, по-видимому, также свойственна специальная структура, однако универсальные обобщения вариационных принципов на необратимые процессы пока неизвестны [1, с. 34].

Условия голономности вариационных уравнений

Вариационное уравнение называется голоном-ным, если его левая часть представляет вариацию некоторого функционала [1, с. 67]. Примером го- лономного вариационного уравнения является уравнение (12), где вариация интегрального функционала, будучи равной нулю, превращает вариационное уравнение в вариационный принцип.

Для увеличения прозрачности приведем рассуждения для конечномерного случая с последующим обобщением для бесконечномерного. В конечномерном случае левая часть ВУ представляет собой линейную дифференциальную форму вида F_k ( u ) 5u_k , где u = { u_k } e R" . Обозначим ее (по повторяющемуся индексу проводится суммирование) через

5 О = F k ( u ) 5u k . (14)

Ясно, что (14) будет вариацией функционала О , если вектор { F_k ( u ) } потенциален, т. е. существует функция ϕ такая, что

F k ( ^u ) = — , ^k = 1, " . ⁽¹⁵⁾ 5 u k

Пусть функции F_k ( u ) непрерывны и дифференцируемы в области A e R " . Пусть 5u_k и δ ' u_k — два бесконечно малых поля в A . Тогда, если обозначить через 5 ' 5 О вариацию формы

5 О вдоль поля 5 ' u_k , а через 55 ' О — вариацию формы 5 ' О вдоль поля 5u_k , то можно сформулировать следующую теорему [1, с. 68].

Для того чтобы форма 5 О представляла в области A вариацию некоторой функции, необходимо и достаточно, чтобы во всех точках этой области было выполнено равенство

5'5 О = 55 ' О .

Отсюда следуют хорошо известные условия го-лономности дифференциальных форм (условия потенциальности вектора {Fk (u)}) [1, с. 68 ]

dFk (u) = dFm (u)

5 um       8 uk   ’ k, m = 1, n.      (17)

Условия голономности (16) имеют локальный характер, т. е. их выполнение в окрестности некоторой точки гарантирует существование в этой окрестности функции ^ ( u ) , такой что 5 О = 5 ( ф ) . Однозначную функцию ϕ можно указать, если область A односвязна [1, с. 68].

Приведенные рассуждения справедливы и в случае бесконечномерных пространств (в частности, в случае теории сплошных сред), и в качестве критерия голономности также справедливо условие (16) [18, 19].

Для иллюстрации приведем пример из [1, с. 69, 70], рассмотренный для функционала

S O — J F ( x , u , u , , u j ) Su d n x ,          (18)

V

где x — { x, } e R n , u , — u , , u j — u j . Условие (16), (17) для функционала (18) имеет вид

af af au, uy

Легко проверяется, что при F — SЛ / Su, где Л —Л ( x , u , u , ) — лагранжиан, зависящий от определяющей функции u и ее первых производных, условие (19) выполняется тождественно.

Замечание . В Физической энциклопедии [16, т. 1, с. 514] в статье о голономных системах определение голономности дано в менее общем виде, чем приведенное выше, а именно: "В аналитической механике под голономной системой понимается механическая система, в которой все наложенные связи являются геометрическими (голономными). Эти связи налагают ограничения только на возможные положения точек и тел системы, но не на их скорости. Разделение систем на голономные и неголономные весьма существенно, т. к. к голо-номным системам применим принцип наименьшего действия, который несправедлив для неголо-номных систем".

КОНКРЕТНЫЙ ПРИМЕР СОСТАВЛЕНИЯ

ВАРИАЦИОННОГО УРАВНЕНИЯ

В этой части работы остановимся на вариационном уравнении для простейшего случая сплошных сред. Исследование более сложных случаев рассмотрим в следующей части работы.

Натянутая гибкая идеальная струна. При описании этого простейшего примера в [11, с. 288–290] продемонстрирован уже упоминавшийся выше прием усреднения при использовании вариационного подхода в сплошных средах на основе методов аналитической механики дискретных частиц.

Процесс колебаний гибкой струны обратим (консервативен). Поэтому в качестве лагранжиана в [11, с. 289] для случая малых колебаний выбран кинетический потенциал

^Л( у , t W , ) = K ^y ) ^{- U} ( y x x ) =

—1 ..',•

k

-

дt    у

1 _T

^y ( x , t )

k   ax   у

V ■ . (20)

Здесь y ( x , t ) — отклонение от состояния равновесия элемента струны с координатой x во времени t ; K и U — линейные плотности соответственно кинетической и потенциальной энергий струны (на единицу ее длины); ρ — линейная плотность струны; T ₀ — натяжение струны.

Найдем S Л ( y_t,у _x ) :

*^{( у} , ■ ^y - ^)— y^Sy , ■ ^y x =

■' sy +   '     sy.       (21)

ay _t a ■       a y _x a x

Выше учтено что операторы и коммути-at    ax руют с оператором δ. После вариации интеграла

t ₂

t ₂

I=Йлd vdt получаем SI = JJ SЛd vdt , где SЛ с t1 V t1 V учетом соответствующего интегрирования по частям и факта равенства нулю вариаций на границах преобразуется к виду

SЛ = -

д дЛ д дЛ ■ кдxдуx дt dytу

n               S Л

Определим величину : δψ

δψ .

SЛ   д дЛ д дЛ

.

Sy     д x д y_x д t д y_t

Записываем условие стационарности действия:

SЛ   д дЛ д дЛ

---—------— о ,

Sy    дxдyx дt дyt что приводит к уравнению колебания струны [11 с. 290]

c 2 a^y-a2y — о    c 2 — T, дx2    д t2     ’          p

Исследуем голономность функционала

S Л ( y _t , y _x ) . Согласно (14) и (21), имеем

^s Q ^{— S Л} ( y ,t y xx ) ^

^ ^F ( u ) ^Su , + ^F 2 ( u ) ^Su 2 ^— ^^" ^Sy , t +^^" ^Sy , x . ^д У t        ^д У , x

Отсюда следует

дЛ       дЛ

Fi = -—, F2 = -—,    5ui = 5v,t, dVt     ^                 (22)

Su ₂ = 5^ x .

Выпишем условие (17) применительно к случаю (22):

д2л  _  д2л

N t t ^д У , x   ^д ^ x ^д ^ t

Отсюда следует что для вариации лагранжиана (20) условия голономности соблюдаются и мы имеем дело с вариационным принципом т. е. поиском стационарного значения интегрального функционала.

ВЫВОДЫ

Для выбора наиболее эффективного механизма математического моделирования взаимосвязанных физических полей в сплошных средах рассмотрено использование в этих целях вариационных подходов. Изложена существующая по этому вопросу теория основанная на использовании вариационных принципов либо составлении вариационных уравнений. Приведено необходимое и достаточное условие при котором решение задачи сводится к использованию вариационного принципа. Приведен и проанализирован конкретный пример составления уравнения движения для простейшей модели сплошной среды — колебания натянутой гибкой струны. Во второй части работы предполагается разбор случаев когда анонсированный подход является единственно возможным для составления математических моделей мультифизичных явлений. В Приложении приведена диссипативная функция (диссипативный потенциал) для случая однородной вязкой теплопроводной жидкости играющая важную роль при моделировании необратимых процессов.

энергии упорядоченного движения в энергию неупорядоченного движения (в конечном счете в тепловую) имеет размерность мощности (и равна потере энергии в единицу времени). ДФ может быть построена для механических систем у которых скорости макроскопических движений малы настолько что силы сопротивления движению можно считать линейно зависящими от скоростей [16 т. 1 с. 653] [20 с. 187]. ДФ ввел впервые Рэлей [9 гл. 4].

ДФ в случае классической механики является квадратичной формой от значений компонентов скоростей [21 с. 102] или тензоров скорости деформации в случае механики сплошных сред и например для случая движения вязкой теплопроводной жидкости с постоянными коэффициентами вязкости ДФ отнесенная к единице объема записывается следующим выражением [13 с. 205] (см. также [16 т. 1 с. 653] [20 с. 187] [22 с. 423] и др.):

Ф = 2 ^ D : D + X9 ² .

Здесь λ µ — параметры Ламе для вязкой изо-

тропной жидкости; D

— тензор скоростей дефор-

маций, D _

равны

^ε xx

ε yy

ε

zz

^ε xx ε yx ε zx

^ε xy ε yy ^ε zy

^ε xz ε yz ^ε zz

а компоненты тензора

д vx дx ’ д Vy дy ’ д vz дz ’

^ε xy

ε yz

ε zx

_ e.

yx

^{_ e} zy

^_ S xz

1 В ,Л

2 (г y    a .x

1В ')

2 ( дz   дy J

• 1    ( д v₇ д v_x ^

z_ +x_ ;2    ( дx   дz J

ПРИЛОЖЕНИЕ

Поскольку наиболее интересными для рассмотрения являются случаи необратимых процессов здесь приводится пример диссипативной функции применительно к случаю однородной вязкой жидкости.

Диссипативная функция (ДФ)

ДФ (функция рассеяния диссипативный потенциал) вводимая для учета влияния сил вязкого трения на движение механической системы и характеризующая степень убывания механической энергии этой системы а также для учета перехода

9 _V- v ; v _ ( v x , v y , v z ) — вектор скорости течения жидкости; D : D — скалярное произведение двух одинаковых тензоров D (определение скалярного произведения см. [13, с. 9])

( dv D : D _| — x ( д x

(дvy Y (дvz )2

— I +1 — I +( дy J ( дz J

|    1 ( ^д v_y дv_z ) 1 ( д v_z дv_x ) 2

I ++ -| +—|      +      |

I 2 ( д z д y J 2 ( д x д z J

I +

1 д v_x    ^д 'vy

+--x- +

2 ( д y    д x

Окончательно имеем

.

Ф = ц < 2

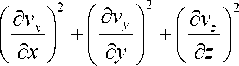
( av   б v,, У+ —-+—-1V ду   дx )

+ хе ² .

+

( ^д v y   дv_z У ( дv_z  дv_x У

+ —- + —- I + 1 —- + —- I

_V д z    д у )   V д x    д z )

> +

количество механической энергии жидкости, которое преобразуется вследствие трения во внутреннюю энергию за единицу времени в единице объема жидкости.

Если для данной среды ДФ известна, то учесть влияние внутреннего трения можно посредством вычисления компонент "диссипативного" тензора σ_i ^' _k по формуле ([16, т. 1, с. 653] и [20, с. 188])

В терминах сдвиговой η и объемной ς вязкостей, для которых справедливы соотношения с параметрами Ламе (см., например, [23]) 2

S = X + — ц , п = Ц , последнее выражение для

ДФ перепишется в виде

' дФ

^ ik = —.

^д ^ к

Тогда результирующий тензор находится как сумма

'

^ k ⁺ ^ к ,

Ф = ц < 2

+

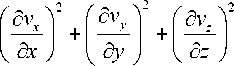
где σ_ik — недиссипативная составляющая результирующего тензора.

( д v,   ^д v y

+ —x+-^

_V д у    д x

I   ( ^д v y    дv_z )    ( дv_z   6 v _х ) ²

I + у_ + z_ I +| z_ + -I

I   ( д z    д у )   ( д x    д z )

> +

(    2     ,

+⁽ s - з п | е ²,

(П1)

что полностью совпадает, например, с выражением в работе [24, с. 342].

Представим Ф в переменных s ik :

^Ф = ² 1 п ZZ ^s ik

V    i = 1 k = 1

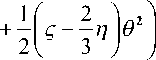
(П2)

где ^е 2 = ( S^xx ^{+ S} yy ^{+ S} zz ^{+ 2 S} xx ^S у, ^{+ 2 S} xx ^S zz ^{+ 2 S} y ^S zx ) , индексы 1, 2, 3 отвечают соответственно переменным x , y и z . Выражение (П1) для ДФ с точностью до множителя 2 совпадает с соответствующим выражением, представленным в работах [16, т. 1, с. 653] и [20, с. 187]. Аналогичное выражение для ДФ, представленное в работе [25, с. 256], отличается от выражения (П1) только отсутствием в нем коэффициента объемной вязкости ς вследствие принятия гипотезы Стокса X = -^ц [25, 2

с. 67], что эквивалентно тому, что X + — ц = 0 или

s = X + 3 ц = 0.

Таким образом, Ф из выражения (П2) является квадратичной формой компонент тензора скоростей деформаций с коэффициентами, характеризующими вязкость среды, и представляет собой то