Вариационный метод для неклассических задач механики с ограничениями, основанный на конечно-элементных аппроксимациях и локальных вариациях
Автор: Баничук Н.В., Макеев Е.В.
Статья в выпуске: 3, 2017 года.
Бесплатный доступ
Статья посвящена решению неклассических вариационных задач механики, заключающихся в минимизации функционалов интегрального вида при ограничениях различного типа. В качестве ограничений рассматриваются различные условия, накладываемые на искомую функцию, доставляющую минимум оптимизируемому функционалу. Учитываемые ограничения включают различные зависимости искомой функции от пространственных координат. Предполагается, что минимизируемый функционал является интегральным и включает зависимость как от искомой функции и пространственных переменных, так и от ее частных производных по пространственным переменным. Предполагается, что включение определенных ограничений в виде неравенств, накладываемых на искомую функцию, отвечает контактным условиям, возникающим в задачах взаимодействия деформируемых тел и задачах контакта этих тел с жесткими препятствиями. Вид возникающих при этом условий характеризует рассматриваемую проблему минимизации функционала с локальными ограничениями, накладываемыми в отдельных точках области определения, как неклассическую задачу вариационного исчисления. Для решения рассматриваемой неклассической задачи вариационного исчисления применяется новый подход, основанный на конечно-элементных аппроксимациях (аппроксимациях Галеркинского типа) и процедурах локального варьирования. При этом исходная область определения минимизируемого функционала и искомой варьируемой функции декомпозируются на отдельные малые подобласти (ячейки области), заполняющие исходную область. Искомая функция задается в узлах разбиения и аппроксимируется в области с применением используемых функций формы. При этом предполагается, что базисные функции формы принадлежат пространству Соболева дифференцируемых с квадратом функций, а базисная система функций является полиномиальной и имеет малую область определения. Ограничения задачи трансформируются в рамках введенных конечно-элементных аппроксимаций. Аддитивный функционал задачи приближенно заменяется интегралами по ячейкам, полностью принадлежащим исходной области. Далее рассматриваемая задача формулируется как задача отыскания узловых значений, удовлетворяющих возникающим неклассическим двухсторонним ограничениям и доставляющих минимум оптимизируемому функционалу. Решение вариационной задачи строится методом последовательных приближений. После выбора начального приближения, удовлетворяющего ограничениям, каждая из итераций выполняет последовательно локальное варьирование искомого решения для всех узлов и осуществляет минимизацию оптимизируемого функционала. При этом на каждом шаге не нарушаются геометрические (контактные) ограничения и осуществляется уменьшение интегральной суммы по ячейкам из окрестности варьируемой точки. После завершения процесса локального варьирования по всем ячейкам и построения обновленного варианта решения процесс повторяется до достижения полной сходимости, при этом постепенно происходит уменьшение шага варьирования и необходимое измельчение конечно-элементной сетки. Таким образом, осуществляется решение рассматриваемой задачи оптимизации. В качестве примера приведено применение предложенного метода к задаче кручения упругопластического стержня. Решение данной вариационной задачи механики численно получено для различных поперечных сечений стержня при различных углах его закрутки на основе предлагаемого подхода. Приводятся полученные и согласующиеся с экспериментальными данными зоны распространения областей пластичности.
Вариационные методы, конечные элементы, задачи с ограничениями, локальные вариации, кручение стержней, упругопластичность
Короткий адрес: https://sciup.org/146211848
IDR: 146211848 | УДК: 539.3 | DOI: 10.15593/perm.mech/2017.3.03
Текст научной статьи Вариационный метод для неклассических задач механики с ограничениями, основанный на конечно-элементных аппроксимациях и локальных вариациях
PNRPU MECHANICS BULLETIN
Вариационные методы играют важную роль во многих разделах механики и применимы как при решении линейных, так и нелинейных задач [1–7]. Эти методы особенно эффективны при решении вариационных задач с различного рода ограничениями. Однако при решении вариационных задач со сложными областями определения оптимизируемых функционалов возникают известные затруднения, связанные с отысканием базисной системы функций. Частично данные трудности преодолеваются на основе вариационноразностных методов [3, 8–11]. Заметим в этом контексте, что эффективное решение широкого класса краевых задач со сложными областями достигается на основе применения метода конечных элементов [12–15]. Однако метод конечных элементов, основанный на построении глобальной матрицы жесткости и решении систем линейных уравнений большой размерности, оказывается не столь эффективным в задачах с локальными ограничениями (в частности, для задач механики контактного взаимодействия, включая задачи с препятствиями, а также задач для сложных конструкций с предельными условиями на перемещения и напряжения), которые требуют разработки нетрадиционных подходов [16–23]. В связи с этим представляется целесообразным разработка методов, основанных на сочетании конечно-элементных аппроксимаций и алгоритмов локального варьирования, использующих преимущества метода конечных элементов и метода локальных вариаций.
Заметим, что классический метод локальных вариаций [24–27] оказался во многих случаях очень эффективным как метод математического программирования. Этот метод требовал минимальной информации для выполнения улучшающих вариаций решения и оказывался особенно эффективным с ограничениями на функции состояния (фазовые переменные).
В настоящей работе развивается альтернативный подход к решению вариационных задач с ограничениями типа неравенств, не требующий использования методов математического программирования. Данный подход основан на методе конечных элементов с аппроксимациями Ритца-Галеркина для искомых функций. В предлагаемом подходе выполняются локальные вариации искомых функций, и проводится сравнение вариаций минимизируемого функционала.
1. Алгоритм метода конечных элементов с локальными вариациями
Предлагаемый алгоритм метода конечных элементов с локальными вариациями рассматривается в контексте следующей задачи.
Требуется найти функцию u ( x ) = u ( x 1 , x 2 ), определенную в области Q в плоскости x 1 x 2 , удовлетворяющую ограничению
( x 1 , x2,u ) е D , ( x 1 ,x 2 ) eQ , (1)
и минимизировать функционал
J ( u * ) = inf „ e d J ( u ), (2)
где
J = J ( u ) = | f ( x 1 , x 2, u , u x i , u x 2 ) d Q , (3)
q a x = {x 1,x2}, f является заданной функцией ее аргументов, множество D задано в трехмерном пространстве x1,x2,u, причем нижними индексами x1,x2 обозначены частные производные.
В частности, в качестве условий (1) будут рассмотрены двусторонние ограничения u- (x 1, x2) < u(x 1, x2) < u+(x 1, x2). (4)
Здесь ( x 1 ,x 2 ) eQudQ ( 5Q = F ), причем u - ( x 1, x 2 ) и u + ( x 1 ,x 2 ) являются заданными функциями в области Q . Для упрощения дальнейших рассмотрений декомпозируем исходную область Q на равные прямоугольные области Q i (ячейки) прямыми линиями. Имеем
Q = UQ i , Q^Q i udQ i , Q , П Q j =0 , i * j,
где N – число ячеек.
Неизвестные величины функции u ( x 1 , x 2 ) в узлах сетки Q i = Q ( x i 1 , x i 2) обозначены как u i , т.е. u i = u ( x i 1 , x i 2) . Решение вариационной задачи представляется в виде
G u (x 1, x 2) = u1U1( x 1, x 2) + ... + нЩ (x 1, x 2) +... + uGUG (x 1, x 2) = ^ukUk(x1,x2), (6)
k = 1
где G – число узлов искомых величин ui , а основные функции Ui(x1,x2) определяются в малых подобластях Q с ячейками Qi в вершинах. Базисные функции Ui принадлежат
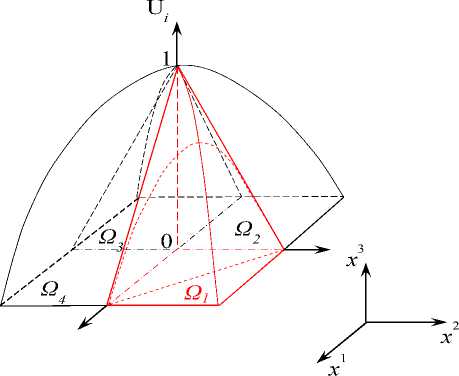
Рис. 1. Базисная функция U i
Fig. 1. The basis function U i
пространству Соболева ( U i е H Q ) и удовлетворяют существенным граничным условиям. Семейство базисных функций удовлетворяет следующим требованиям (рис. 1):
-
1) U , ( x 1 , x 2) е C ( Q );
-
2) U i * 0 только для тех элементов, которые соединены с узлами с узлами Qi ;
3) U ( x * , x 22 ) = <
-
1, если i = j , 0, если i * j ;
-
4) U i(e ) являются сужением U i на Q e , где ( U i ) „ e = U i1' 1 .
Таким образом, искомое решение удовлетворяет следующему равенству:
G u (xj, x22) = ^ uiUi (x1, x2) = uj. (8)
i = 1
Заметим, что билинейный полином
U i e ) = a 0 + a 1 x 1 + a 2 x 2 + a 3 x 1 x 2 (9)
применяется в качестве ограничивающей функции для прямоугольных ячеек (элементов), коэффициенты которой должны удовлетворять третьему условию соотношения (7). Множество узлов и элементов, принадлежащих области Q , составляют конечно-элементную сеть. При этом мы получаем базисную систему функций, которые являются полиномиальными и имеют малую область определения.
Ограничения (1) и (4) трансформируются в рамках конечно-элементных аппроксимаций как
( x 1 , xf,u) g D , (10)
u - ^ u ^ ut, (11)
где u - = u - ( x 1 , x i 2 ), u i + = u + ( x i 1 , x i 2 ) .
Представленный интеграл (3) приближенно заменяется суммой интегралов по ячейкам, полностью принадлежащим области Q + Г (число ячеек обозначается через N ). Имеем
N
J = J ( u ) = £ J ( j )( u ), (12)
j = 1
J ( j ) = j f ( x 1 , x 2, u ( j ), u^,u^f^)d Q . (13)
^ j
В итоге преобразований рассматриваемая задача (1), (2), (3) и (4) может быть сформулирована как задача отыскания ui , удовлетворяющих ограничениям (10) (или (11)) и доставляющих минимум функционалу (12), (13).
Решение задачи минимизации функционалов (12), (13) будем строить последовательными приближениями. В качестве начального приближения для ui возьмем любой набор чисел, удовлетворяющих (10) (или (11)). При выборе начального приближения желательно учесть имеющуюся априорную информацию о предполагаемом решении, различные качественные, физические или иные соображения. Удачный выбор начального приближения может ускорить сходимость метода.
Приведем предлагаемый метод последовательных приближений. Зададимся некоторым малым положительным числом h , которое будем дальше называть шагом варьирования.
На каждом шаге итерационного алгоритма операции последовательно выполняются для всего набора узлов, при этом для каждого узла операция выполняется только один раз. Для нахождения нового значения ui для каждого узла рассмотрим в качестве новых возможных значений старое значение u , а также величины u i + h и u i - h . Отметим, что при вычислении функционала J потребуется пересчет в (12), (13) компоненты максимум только для четырех ячеек, связанных с ui , т.е. это слагаемое связано с ячейками, лежащими полностью в области Q + Г и содержащими точку ( x ' , x f ) в качестве узла. Определим эту величину как П i .
В результате будем производить замену старого значения и на величины u + h или U - h , так, если для данных величин выполняются ограничения (10) (или (11)) и происходит уменьшение функционала J , т.е.
(x1, x2, Ui ± h) е D(14)
или u-< и ± hi < u +,(15)
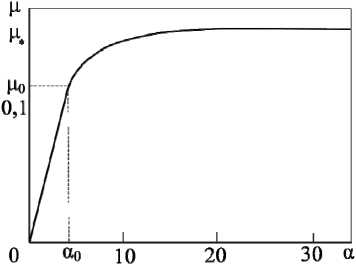
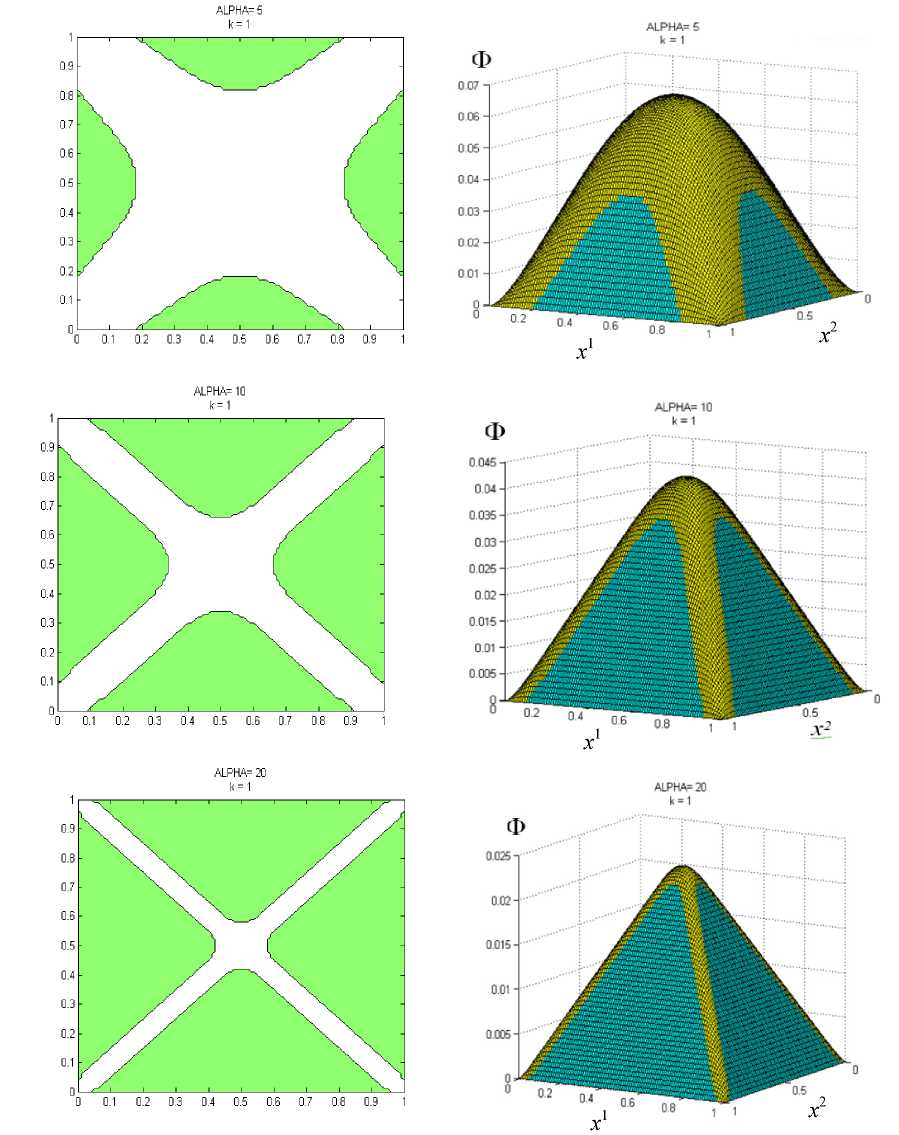
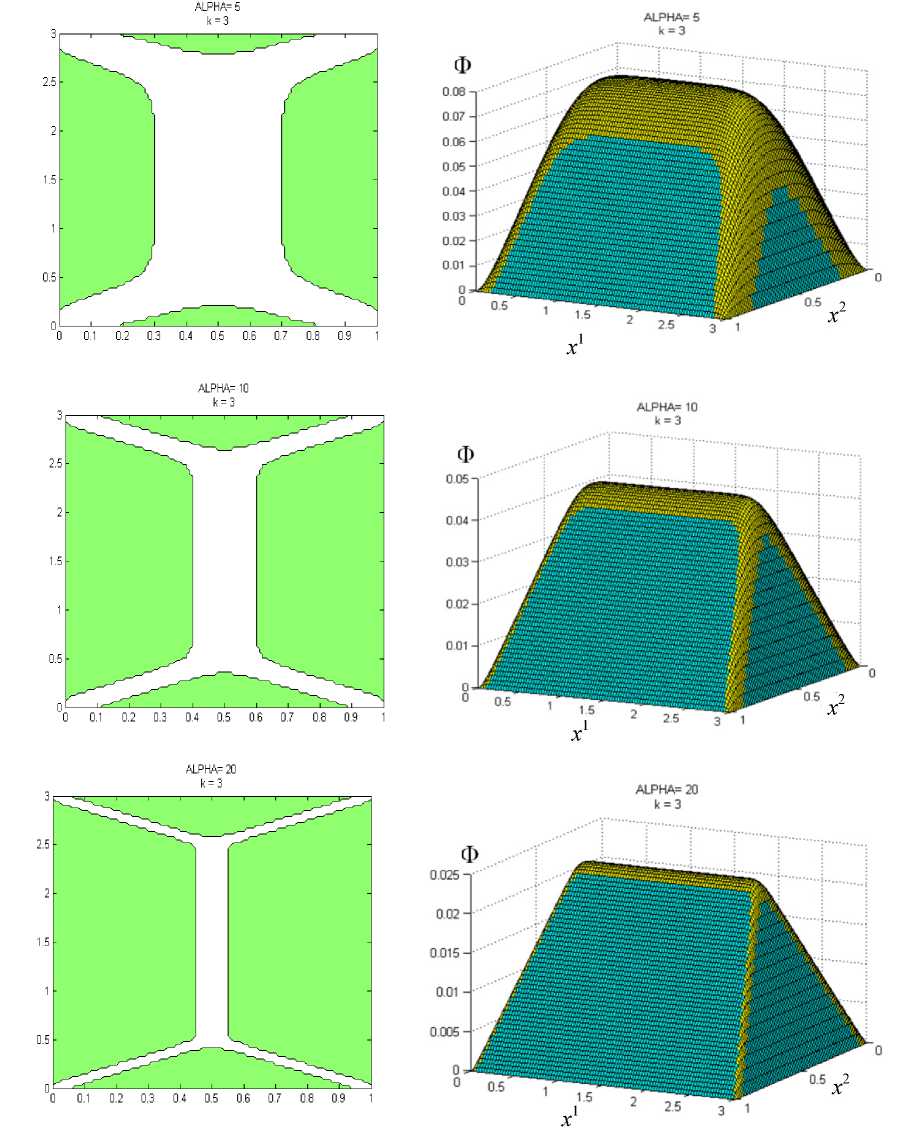
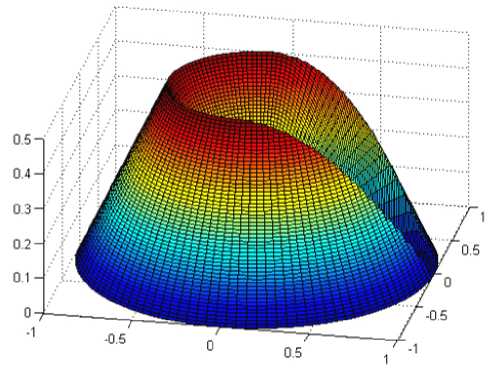
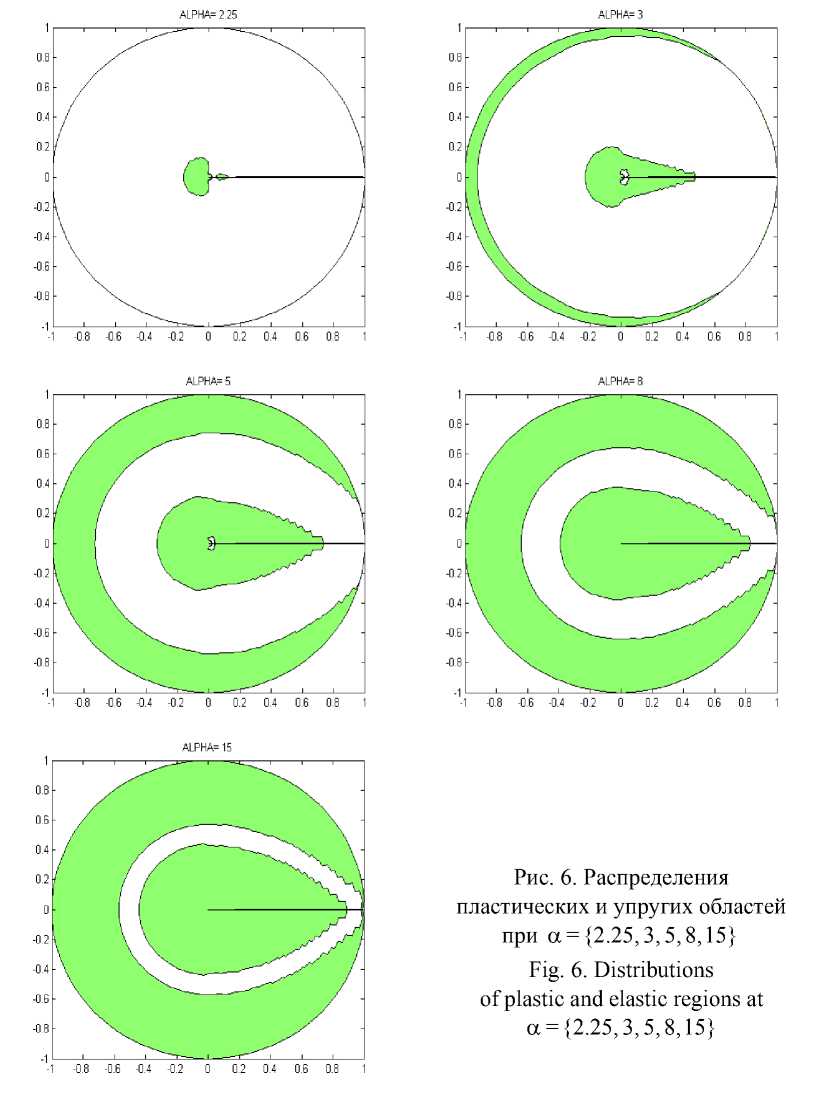
и выполняется неравенство п±=пi(ui ±h) и(x 1,x2) = u1U 1(x 1,x2) +... + (ui ± hи(x 1,x2) +... + uGUG(x 1,x2) .(17) Затем алгоритм переходит к следующему узлу. В противном случае в качестве решения принимается старое значение ui . Число вычислительных операций может быть сокращено, если в качестве приоритетного направления изменения узлового значения будет приниматься направление, на котором происходит максимальное уменьшение функционала для предыдущего узла. После завершения итераций по всем узлам мы повторяем процедуру, пока не будет достигнута полная сходимость для выбранных значений Ax 1, Ax2, h , другими словами, пока значения ui не перестанут меняться. После полной сходимости итераций с данными Ax1, Ax2, h уменьшим шаг варьирования h вдвое и снова будем проводить итерации описанным выше образом. Будем считать, что приближенное решение на указанной сетке получено, когда будут обеспечены условия полной сходимости итерационного процесса для некоторого малого h, удовлетворяющего условию h = o (min{(Ax 1)2,(Ax2)2}). (18) Для получения уточненного решения можно использовать более мелкую сетку с большим числом узлов за счет уменьшения величин Ax1, Ax2. Начальным приближением решения на новой сетке служит уже полученное ранее решение. Итерационный процесс повторяется для новой сетки с уменьшающимися значениями h, как было описано выше. Процесс решения заканчивается при полной сходимости итераций для некоторых достаточно малых Ax1, Ax2, h, удовлетворяющих (18). 2. Упругопластическая задача Моделирование упругопластического кручения прямых стержней будем проводить на основе деформационной теории пластичности неупрочняющегося материала (для односвязной области). В качестве примера применения описанного выше алгоритма приведем решение задачи кручения упругопластического стержня, записываемой в виде J "J 1(ф21 +ф2.)-2Y<№ _ 2 dx1dx2^ min, (19) u Ф = 0 на Г = dQ, Ф2 + Ф22< т2 в Q, x1x20 где γ – модуль сдвига; τ0 – предел текучести при чистом сдвиге; θ – угол закрутки, приходящийся на единицу длины стержня; Q - односвязная область поперечного сечения стержня; Г = SQ - граница области Q, Ф = Ф (х 1, х2) - функция сдвиговых напряжений, такая, что Т13 =Ф x 2, Т23 =-Ф х, а т13, т23 - сдвиговые компоненты тензора напряжений соответственно в плоскостях х1х3, х2х3 (х3 соответствует направлению по оси, перпендикулярной плоскости х1х2). Минимум функционала (19) разыскивается на классе функций Ф = Ф(х 1,х2), удовлетворяющих условиям (20), (21). Если решение задачи (19)–(21) найдено, то скручивающий момент подсчитывается по формуле M = 2J Ф(х 1, х2)dx1dx2. Q Далее используются безразмерные переменные и обозначения х ~2 х Л Ф •х1 = —, х2 = , Ф =-----Т, dd2γθd2 2γθd M а = ’ Ц = Э 3 ’ τ0 2τ0d где d - характерный размер области Q, а а - параметр задачи. В последующем тильда у безразмерных переменных опускается. В безразмерных переменных основные соотношения рассматриваемой задачи записываются в виде Ф2 +Ф22 < а-2, xx (25) Ф 1 1+ Ф 2 2 = —1 , x1x1 x2x2 (26) Ф = 0 на Г = dQ, ц = а J Ф( х 1, х2) dx1dx2, Q (27) (28) Ф dx1dx2. j = Г 1 (ф2 +ф 22) J 9 V х х / n L 2 Q Решение задачи упругопластического кручения значительно упрощается, если воспользоваться следующим преобразованием. Вместо дифференциального неравенства (25) можно воспользоваться непосредственным неравенством Ф(х 1,х2) < Т(х 1,х2), наложенным на функцию состояния Ф(х 1,х2). Здесь Т(х 1,х2)решение более простой геометрической задачи чисто пластического кручения, описываемого следующими соотношениями: Т 2, + Т 22< а 2 в Q, Т 0 на Г = dQ. x1x2 Это так называемая аналогия Надаи [28,29], приводящая к построению «пластической крыши», описываемой функцией Т(x 1,x2). Результаты вычислений μ представлены в таблице для прямоугольных областей поперечных сечений при различных углах закрутки стержня а = {20/3, 10, 20, 40,80} и для различных отношений длин сторон прямоугольников k. Скручивающий момент μ для различных α и k Torsion moment μ for various α and k k α0 μ0 α = 20/3 α = 10 α = 20 α = 40 α = 80 1 2,9629 0,1025 0,1560 0,1624 0,1657 0,1664 0,1666 1,5 2,3585 0,1701 0,2780 0,2859 0,2903 0,2913 0,2916 2 2,1505 0,2418 0,3999 0,4093 0,4149 0,4162 0,4165 3 2,0305 0,3988 0,6418 0,6559 0,6640 0,6660 0,6665 4 2,0021 0,7285 1,1269 1,1490 1,1625 1,1654 1,1662 Приведем сначала качественное описание решения. При малых значениях α ограничения не достигаются в области Q. В этом случае решение Ф = Ф0 (x1, x2) соответствует чисто упругому кручению. Пластические зоны появляются, когда а = а0 = Рис. 2. Зависимость момента кручения μ от угла закрутки а Fig. 2. The torsion moment μ as a function of twist angle а Этот угол закрутки находится из решения задачи об упругом кручении стержня. В интервале 0 < а < а0, как следует из (28), имеем α Ц = Цо —, α ц0= ц(а0) = а0j Ф0dx1dx2 . (34) n При а > а0 пластические области увеличиваются с увеличением α . Момент кручения μ является монотонно возрастающей функцией (рис. 2), а ц, соответствует чисто пластической закрутке ( а = да ). На рис. 3 и 4 показано развитие пластических областей и 3D-графики функции Ф для прямоугольных областей Q c к = 1(а={5,10,20}) и к = 3(а={5,10,20}) . При проведении расчетов использовалась сетка размером 100x100, а шаг варьирования изменялся от h0 = 0,001 до h, = 10-8. В качестве начального приближения выбиралась Ф0 = 0,5Т. Численное решение находилось для задачи с ограничением, заданным выраже- нием (30). Полученные пластические зоны обозначены зеленым цветом, упругие – белым. Приведенные ниже рисунки для функции напряжений Ф показывают, как при выполнении расчетов искомая функция напряжений выходит на наложенные на нее ограничения, и как следствие зоны выхода функции Ф на ограничения являются зонами возникновения пластичности (обозначены темно-зеленым цветом) Зоны, где ограничения не достигаются, зоны упругого поведения материала обозначены светло-зеленым цветом. Рис. 3. Пластические зоны и 3D-графики функции Ф в случае к = 1 а = {5,10,20} и Fig. 3. Plastic zones and 3D-graphs of function Ф for к = 1 and a = {5,10,20} Рис. 4. Пластические зоны и 3D-графики функции Ф в случае к = 3 и а = {5,10,20} Fig. 4. Plastic zones and 3D-graphs of function Ф for к = 3 and а = {5,10,20} Рассмотрим задачу упругопластического кручения стержня круглого поперечного сечения Q : 0 < r < 1,0 < ф < 2n, имеющего радиальный разрез 0 < r< 1, ф = 0. Здесь используются цилиндрические (полярные координаты) r, φ . Выражение, определяющее «пластическую крышу», т.е. функцию Т(r, ф), имеет вид [30] Т (r, ф) = < r — | sin ф | при 0 < r< α 1 - r -------, и 0 < ф < П, — < ф < 2л, 1+ | sin ф | 2 2 r — при ----- а 1+ | sin ф | 1π < r< 1, и 0 < ф < П, — < ф < 2п, 22 3π α 1 - r — < ф < —, 2 α 1π 3π при — < r < 1, — < ф < — 3π и функция Т(r, ф) (рис. 5) для а = 1. Рис. 5. Функция пластических напряжений Fig. 5. Function of plastic stresses Решение неклассической вариационной задачи минимизации функционала -Ф > r drdф производилось на классе функций, удовлетворяющих ограничениям Ф(r, ф) <Т(r, ф) в Q, Ф(r, ф) = 0 на r=5Q, (39) где функция Т определялась формулой (37), включающей зависимость от угла закрутки α . (Функционал (38) приведен в безразмерной форме по аналогии с (29)). Численное решение с применением описанного в работе алгоритма разыскивалось на конечно-элементной сетке: rj = jAr, Ar = 0.01, j = 0,1,...,100, ф,= i Аф, Аф = 1—00, i = 0,1,....,100. Все вычисления производились при а = {1, 2, 2.25, 3, 4,...,15}, а шаг варьирования изменялся от h0 = 0,0001 до h, = 10-8. В качестве начального приближения выбиралась Ф0= 0,5 Т. Полученные при этом распределения пластических (зеленый цвет) и упругих областей (белый цвет) показаны на рис.6 для значений а = {2.25,3,5,8,15}. При расчете взаимодействие берегов разреза не учитывалось, и контактная задача с трением не решалась. Полученные численные решения соответствуют результатам, приведенным в [30]. Сравнение по времени решения упругопластических задач кручения, рассмотренных в данной работе, с методами, приведенными в [30], показало существенное сокращение необходимого времени (3–5 раз) с учетом многих факторов реализации алгоритма.
3. Некоторые замечания и обобщения Выше была описана простейшая версия сочетания конечно-элементных аппроксимаций и метода локальных вариаций. Рассмотрим кратко некоторые возможные модификации предложенного алгоритма. Так, например, в рамках предложенного алгоритма возможны как другие способы дискретизации (триангуляции) области определения функционала, так и другие полиномиальные базисные функции (функции формы). Шаг варьирования h на рассматриваемой текущей итерации может меняться при переходе от одного узла к другому. При этом могут рассматриваться алгоритмы с локально оптимальными шагами варьирования hi , выбираемыми из условия максимального убывания функционала по четырем ячейкам, имеющим общий узел в точке (xi1,xi2). Отметим теперь некоторые обобщения формулировки задачи (1)–(4), для которых описанный алгоритм, основанный на конечно-элементных аппроксимациях и использовании локального варьирования, может эффективно применяться. 1. Искомая функция u(xi1,xi2), входящая в соотношения (1)–(4), может быть вектором-функцией с компонентами u1,...,uk. В этом случае улучшающие вариации выполняются последовательно для каждой компоненты ui(i= 1,...,k) при фиксированных значениях остальных компонент. 2. Описанный подход применим к вариационным задачам, в которых интегральный функционал (2), (3) зависит от производных более высокого порядка от искомой функции. Для вычисления этих производных и выполнения локальных вариаций функции u в одном узле сетки требуется вычисление большего числа слагаемых в сумме (12) или использование полиномиальных базисных функций более высокой степени. Последнее означает применение h- p конечно-элементных аппроксимаций. 3. Данный алгоритм применим к многомерным вариационным задачам, в которых искомая функция зависит от трех и большего числа переменных (u(x1, x2, x3,...) ), а интеграл (3) берется по области соответствующей размерности. В этом случае алгоритм решения вариационной задачи модифицируется естественным образом. В качестве элементарных ячеек принимаются параллелепипеды соответствующей размерности, а при локальной вариации u в одном узле рассматриваются изменения интегралов по большему числу ячеек ( ≥8), лежащих в окрестности данного узла. 4. Предложенный алгоритм легко адаптируется для нерегулярных сеток разбиения области, в том числе для сеток с переменным шагом разбиения. Работа выполнена при финансовой поддержке РНФ (проект РНФ № 17-19-01247).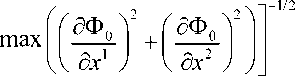
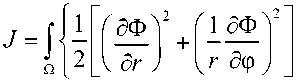
Список литературы Вариационный метод для неклассических задач механики с ограничениями, основанный на конечно-элементных аппроксимациях и локальных вариациях
- Михлин С.Г. Вариационные методы в математической физике. -М.: Наука, 1970. -512 с.
- Михлин С.Г. Численная реализация вариационных методов. -М.: Наука, 1966. -681 c.
- Михлин С.Г., Смолицкий X.Л. Приближенные методы решения дифференциальных и интегральных уравнений. -М.: Наука, 1965. -343 c.
- Ректорис К. Вариационные методы в математической физике и технике. -M.: Мир, 1985. -590 c.
- Васидзу К. Вариационные методы в теории упругости и пластичности. -М.: Мир, 1987. -542 с.
- Bisci G.M., Radulescu V.D., Servadei R. Variational Methods for Nonlocal Fractional Problems (Encyclopedia of Mathematics and its Applications). -Cambridge: Cambridge University Press, 2016. -400 p.
- Cassel K.W. Variational Methods with Applications in Science and Engineering. -Cambridge: Cambridge University Press, 2013. -432 p.
- Haslinger J. Neittaanmaki P. Finite Element Approximation for Optimal Shape Design: Theory and Applications. -Chichester: John Wiley and Sons Ltd, 1988. -334 p.
- Glowinski R. Numerical Methods for Nonlinear Variational Problems. -Berlin-Heidelberg-New York-Tokyo: Springer-Verlag, 1984. -354 p.
- Баничук Н.В. Введение в оптимизацию конструкций. -М.:Наука, 1986. -304 c.
- Kukudzhanov V.N. Numerical Continuum Mechanics. -Berlin, Boston: Walter de Gruyter, 2013. -429 p.
- Ciarler P.G. The Finite Element Method for Elliptic Problems. -Amsterdam: North-Holland Publishing Company, 1978. -321 p.
- Norrie D.H., G. de Vries. An introduction to finite element analysis. -New York: Academic Press, 1978. -301 p.
- Bathe K.J. Finite Element Procedures in Engineering Analysis. -New Jersey: Prentice-Hall, Englewood Cliffs, 1982. -727 p.
- Bathe К.J, Wilson E.L. Numerical methods in finite element analysis. -New Jersey: Prentice-Hall, Englewood Cliffs, 1976. -528 p.
- Sauer R.A. Local finite element enrichment strategies for 2D contact computations and a corresponding post-processing scheme//Computational Mechanics. -2013. -Vol. 52 (2). -P. 301-319.
- Sofonea M., Tiba D. The control variational method for elastic contact problems//Annals of the Academy of Romanian Scientists. Series on Mathematics and its Applications.-2010. -Vol. 2. -No. 1. -P. 99-122.
- Wriggers P, Zavarise G. Computational contact mechanics. In E. Stein, R. de Borst and T.J.R. Hughes, editors, Encyclopedia of Computational Mechanics. -Chichester: John Wiley & Sons. -2004. -Vol. 2. -P. 195-226.
- Zavarise G., Wriggers P. (Eds.) Trends in Computational Contact Mechanics. -Berlin; Heidelberg: Springer-Verlag, 2011. -354 p.
- Бураго Н.Г., Кукуджанов В.Н. Обзор контактных алгоритмов//Изв. РАН. Механика твердого тела. -2005. -№ 1. -C. 45-87.
- Páczelt I., Mróz Z. On optimal contact shapes generated by wear.//International Journal for Numerical Methods in Engineering. -2005. -Vol. 63(9). -P. 1250-1287.
- Laursen T.A. Computational Contact and Impact Mechanics: Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis. -Berlin: Springer-Verlag, 2002. -454 p.
- Matei A. An evolutionary mixed variational problem arising from frictional contact mechanics//Mathematics and Mechanics of Solids. -2014. -Vol. 19. -Iss. 3. -P. 225-241.
- Черноусько Ф.Л. Метод локальных вариаций для численного решения вариационных задач//Журнал вычислительной математики и математической физики. -1965. -T.5, №4. -C. 749-754.
- Баничук Н.В., Петров В.М., Черноусько Ф.Л. Численное решение вариационных и краевых задач методом локальных вариаций//Журнал вычислительной математики и математической физики. -1966. -T. 6, № 6. -C. 947-961.
- Баничук Н.В., Петров В.М., Черноусько Ф.Л. Метод локальных вариаций для вариационных задач с неаддитивными функционалами//Журнал вычислительной математики и математической физики. -1969. -T. 9, № 3. -C. 548-557.
- Баничук Н.В. Оптимизация форм упругих тел. -M: Haука, 1980. -256 с.
- Nadai A. Plastic torsion, an experimental determination of the stress distribution in a bar which has been twisted to the limit of plasticity//Proc. ASME, Mech. Division. -1931.
- Nadai A. Theory of flow and fracture of solids. Vol. 1. -New York; Toronto; London: McGraw-Hill, 1950. -229 p.
- Черноусько Ф.Л., Баничук Н.В. Вариационные задачи механики и управления (Численные методы). -М.: Наука, 1973. -240 c.


