Вариационный подход к расчёту функции эйконала

Задача расчёта оптического элемента из условия формирования заданного распределения освещённости в некоторой плоскости относится к классу обратных задач неизображающей оптики и является крайне сложной. В большинстве случаев данная задача сводится к решению нелинейного дифференциального уравнения эллиптического типа. Методы расчёта оптических поверхностей, основанные на прямом численном решении уравнения данного типа, появились только в последние годы [1 –4]. Общим недостатком указанных методов является высокая вычислительная сложность. Поэтому для решения обратных задач неизображающий оптики широко используются различные итерационные методы. Одним из универсальных и широко используемых итерационных методов является метод согласованных квадрик (МСК, supporting quadric method) [5– 12]. Наиболее известен вариант метода для расчёта зеркал или преломляющих оптических элементов, формирующих дискретные распределения интенсивности (освещённости) в виде набора точек. В зависимости от задачи в качестве квадрик используются параболоиды, эллипсоиды или гиперболоиды. В частности, в задаче расчёта зеркал поверхность зеркала представляется в виде набора сегментов параболоидов (задача формирования распределения интенсивности в дальней зоне) или эллипсоидов (задача фокусировки в набор точек в ближней зоне) с определёнными параметрами. При этом число сегментов равно числу точек фокусировки. Расчёт параметров параболоидов (эллипсоидов) осуществляется итерационным методом, при этом сходимость метода строго доказана [6]. В работе [12] предложена модификация МСК для расчёта функции эйконала светового поля из условия фокусировки в набор точек. Данная задача является важной при рас- чёте дифракционных оптических элементов, в особенности преобразователей формы пучка [13]. Кроме того, по функции эйконала может быть восстановлена рефракционная оптическая поверхность, что позволяет применять предложенный метод для расчёта преломляющих оптических элементов [14].

Основными достоинствами МСК являются его универсальность и возможность формирования сложных дискретных изображений. В то же время при решении светотехнических задач обычно требуется формирование непрерывных распределений в областях относительно простой формы (прямоугольник, эллипс, треугольник и т.п.). В базовых теоретических работах [11, 15] показано, что проблема расчёта зеркала для формирования заданного непрерывного распределения интенсивности в дальней зоне может быть сформулирована как вариационная задача минимизации функционала и как задача Монжа–Канторовича о перемещении масс со специальной функцией стоимости. Важным практическим результатом указанных работ является сведение вариационной задачи к задаче линейного программирования (ЗЛП). В силу специфического вида матрицы ограничений, для решения соответствующей ЗЛП существуют эффективные алгоритмы, обладающие полиномиальной сложностью [16]. Расчёт зеркал на основе решения ЗЛП рассмотрен в [17, 18].

В настоящей работе вариационный подход из работ [11, 15] впервые применён к решению задачи расчёта функции эйконала светового поля. Показано, что задача расчёта функции эйконала из условия фокусировки в заданную область также может быть сформулирована как вариационная задача и как задача Монжа–Канторовича о перемещении масс. Отметим, что в отличие от работ [11, 15], в задаче расчёта эйконала не требуется выполнение условия дальней зоны. Под массами в задаче Монжа-Канторовича понимаются исходное распределение освещённости и требуемое распределение освещённости в области фокусировки. При этом получено, что функция стоимости соответствует расстоянию между точкой исходной плоскости (в которой задана функция эйконала) и точкой области фокусировки. Данный результат показывает, что решение обратной задачи расчёта эйконала соответствует отображению, для которого минимизируется суммарное расстояние между точками исходной плоскости и области фокусировки. Предложенный формализм позволяет свести расчёт функции эйконала к ЗЛП. При этом расчёт отображения, соответствующего функции эйконала, может быть сведён к решению линейной задачи о назначениях [19]. В качестве примеров рассчитаны функции эйконала из условия фокусировки пучка круглого сечения в прямоугольную область. По функциям эйконала рассчитаны преломляющие оптические элементы.

Текст статьи организован следующим образом. В параграфе 1 приведена постановка задачи. В параграфе 2 определяется так называемое слабое (обобщённое) решение задачи. В параграфе 3 сформулирована соответствующая вариационная задача. В параграфе 4 рассмотрена связь вариационной задачи с задачей Монжа-Канторовича. В параграфе 5 рассмотрен расчёт функции эйконала из условия фокусировки пучка круглого сечения в прямоугольную область. Расчёт проведен на основе решения ЗЛП и задачи о назначениях. Для удобства читателя доказательства лемм и теорем вынесены в приложения.

1.    Постановка задачи

Пусть в области G, расположенной в плоскости z = 0, задано световое поле c распределением освещённости E0(и 1, и2) и функцией эйконала Ф0(и 1, и2), где (и 1, и2) - декартовы координаты. Область G будем называть апертурой. Обозначим r ( Ui, и 2) = ^ф и1, фи 2, V1 -^Ф)2 ^

единичный вектор луча для среды с показателем преломления n =1, где Ф ui = д Ф/ д и, i =1,2, У Ф=(Ф и ₁ , Ф и ₂ ). Рассмотрим «лучевое отображение» у _Ф области G в область на плоскости z = f >0, задаваемое функцией эйконала Ф( и 1 , и ₂). В данном отображении точка ( x 1 , x ₂) = у _Ф( и 1 , и ₂) определяется как точка пересечения луча с плоскостью z = f (рис. 1):

• [ . / Г.

• Х 1 = u i + Ф и f J1 - ( УФ ) ,

1 ¹ /г-—— (1) [ x 2 = U 2 +Ф и 2 f ] ^1- ( УФ )² .

Для удобства записи далее будем использовать следующие обозначения. Точки ( и 1 , и ₂) и ( x 1 , x ₂) будем обозначать и и x соответственно. Интеграл по d и (d x ) будет обозначать двойной интеграл по d и 1 d и ₂ (d x 1 d x ₂).

Распределение освещённости в области фокусировки определяется из закона сохранения энергии вдоль лучевых трубок в виде:

E ( x ) = E (У ф ( и ) ) = E о ( и ) / J (у ф ( и ) ) ,            (2)

где J ( у _Ф( и )) = д x 1 /д и 1 - д x ₂/д и ₂-д x ₂/д и 1 - д x 1 /д и ₂ - якобиан преобразования координат (1).

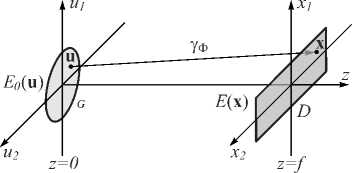
Рис. 1. Геометрия задачи расчёта функции эйконала

Соотношение (2) может быть представлено в интегральном виде:

j E о ( и )d и = j E ( x )d x ,

У,»       а

где ас G - любая область (любое измеримое подмножество). Закон сохранения энергии может быть также записан в следующем виде (аналогично см. лемму 4.9 в [11])

G

j h ( у , ( и )) E о ( и )d и = j h ( x ) E ( x )d x ,

D

где h ( x ) - любая непрерывная функция.

Сформулируем обратную задачу расчёта эйконала светового поля из условия формирования заданного распределения освещённости. Требуется рассчитать функцию эйконала Ф ( и ), и е G , индуцирующую биективное лучевое отображение у _Ф: G ^ D , которое формирует в области D плоскости z = f заданное распределение освещённости E ( x ), x е D (рис. 1).

2.    Слабое решение

В работах [11, 15], посвященных расчёту зеркала для формирования заданного распределения интенсивности в дальней зоне, вводится понятие так называемого слабого (обобщённого) решения. В данном параграфе мы введём аналогичное понятие для задачи расчёта функции эйконала.

Подставляя (1) в (2), можно видеть, что расчёт функции Ф( и ) сводится к решению нелинейного дифференциального уравнения в частных производных эллиптического типа. Требование дифференцируемости функции эйконала Ф( и ) и отображения у _Ф( и ) существенно ограничивает класс решаемых задач (класс формируемых распределений освещённости). В связи с этим введём понятие слабого (обобщённого) решения, позволяющего расширить класс допустимых функций Ф( и ). Для определения слабого решения рассмотрим метод построения функции эйконала Ф( и ) из эйконалов линз с фокусами в точках x е D [12]. Под функцией эйконала линзы Ф l (и; x ) понимается такая функция эйконала в плоскости z = 0, при которой все лучи приходят в точку x в плоскости z = f. Из (1) несложно получить, что функция эйконала линзы имеет вид:

Ф 1 ( и ; x ) = т ( x ) -р ( и , x ), (5)

где р ( u , x ) = ^f ² + ( x - и ) ² - расстояние между точками с координатами ( и ь и ₂,0) и ( x ь x ₂, f ). Действительно, подставляя (5) в (1), получим, что x = у _Ф( и ). Кроме того, заметим, что уравнение (5) при z = 0 соответствует эйконалу сходящегося сферического пучка V sb ( и , z ) = - J ( f - z )² + ( x - и )² + V ( x ) с фокусом в точке x е D , записанному при z = 0. При этом константа V ( x ) соответствует значению эйконала в точке фокусировки. Функция эйконала для фокусировки в заданную область D может быть представлена в виде огибающей семейства функций (5) по параметрам x = ( x 1 , x ₂) е D [12]. Действительно, по определению, огибающая поверхность касается каждой функции эйконала в семействе (5) в некоторой точке. При этом частные производные огибающей поверхности совпадают в точке касания с частными производными эйконала линзы. Направление луча определяется частными производными функции эйконала. Поэтому лучи, соответствующие эйконалу в виде огибающей поверхности, будут направлены на точки области D , которые являются фокусами линз в (5). Уравнение огибающей поверхности для семейства эйконалов линз (5) имеет вид [12]:

Ф i ( и ; x ) = V ( x ) -р ( и , x ),

V"(v( x ) -р ( и , x ) ) = 0,                        (6)

1 " x ¹

—(^V ( ^x ) ^- р ^{( и} , ^x ) ) = 0.

_ д x ₂

Система уравнений (6) содержит эйконал линзы (первое уравнение) и производные данного уравнения по параметрам ( x ₁, x ₂) (второе и третье уравнения). Отметим, что второе и третье уравнения в системе (6) являются необходимым условием экстремума функции (5) по переменным ( x ₁, x ₂) при фиксированном значении и = ( и ₁, и ₂). Данное условие соответствует принципу Ферма и позволяет представить функцию эйконала в переменных ( и ₁, и ₂) в виде:

Ф( и) = max (v( x )-р( и, x)), xeD x x 7           ’ или

Ф ( и ) = min ( v( x ) -р ( и , x ) ) . x е D ^{v 7 7           7}

Заметим, что максимум в формуле (7) для Ф( и ₀) достигается в точке x ₀ такой, что x ₀ = у ( и ₀). Действительно, пусть максимум достигается в точке x ₀, тогда функция эйконала линзы V ( x ₀)- р ( и , x ₀) касается функции Ф( x ₀) в точке и ₀. Поскольку обе функции дифференцируемы, то производные Ф в этой точке совпадают с производными функции эйконала линзы, а отображение у задаётся производными функциями, то у _Ф ( _{и 0} ) совпадает с образом точки и ₀ под действием отображения у , индуцированного функцией эйконала линзы с фокусом в x ₀. Аналогично для функции Ф, определяемой формулой (8).

Представления (5) зависят от функции V ( x ), которая определяет распределение энергии в области фокусировки. По построению функция V ( x ) соответствует эйконалу в области D и также может быть представлена в виде огибающей семейства эйконалов линз, заданных в области D и фокусирующих в точки и е G . Функция эйконала линзы, обеспечивающая фокусировку из области D в точку и е G , имеет вид:

V i ( x ; и ) = Ф ( и ) + р ( и , x ),                           (9)

где константа Ф( и ) соответствует значению эйконала в точке фокусировки. Отметим, что в отличие от (5), величина р( и , x ) входит в (9) с противоположным знаком. Это связано с тем, что в данном случае лучевое отображение определяется «инвертированным» единичным вектором луча

r ( x 1 , x 2 ) = - ^ V x 1 , V x 2 , V1 - (W) ²

который имеет отрицательную компоненту z . Кроме того, заметим, что уравнение (9) соответствует эйконалу сферического пучка

• V sb ( x , z ) = ^ z ² + ( x - и ) ² +V ( x ) ,

расходящегося из точки ( и , 0), записанному при z = f. Огибающая семейства (9) по параметрам и = ( и ₁, и ₂) имеет вид:

V i ( x ; и ) = Ф ( и ) + р ( и , x ),

• -^-(ф( и ) + р ( и , x ) ) = 0,                        (10)

’ ^{д и 1}

( ^ф ( и ) + р ( и , x ) ) = 0.

_ д и ₂

Второе и третье уравнения в системе (10) являются необходимым условием экстремума функции (9) по переменным ( и ₁, и ₂) при фиксированном значении x = ( x ₁, x ₂). Это позволяет представить функцию в виде:

V( x) = max (ф (и ) + р (и, x)),(11)

иeG х7

или

V( x) = min (ф( и ) + р (и, x)).(12)

иeG v7

Покажем, что если прямое отображение уФ: G ^D определяется функцией (7), то обратное отображение уф1 : D ^ G определяется функцией (12). Действительно, пусть xо = уФ(и0), где x0 = argmax(v(x)-р(и0,x)).

x e D

Покажем, что в этом случае и ₀= y_V ( x ₀). Докажем это от противного. Предположим, что и ₁= y_V ( x ₀), где и ₁ * и ₀. В этом случае, согласно (12), будем иметь

V ( x 0 ) = Ф ( и 1 ) + р ( и 1 , x 0 ) < Ф ( и 0 ) + р ( и 0 , x 0 )

и Ф(и0)> V(x0)- р (и0, x0). Последнее неравенство противоречит исходному условию x0=уФ (и0), согласно которому Ф( u 0)> Т(x 0)- р (и о, x о). Таким образом, Yt = Yф1. Аналогично можно показать, что если прямое отображение YФ: G НD определяется функцией (8), то обратное отображение Yф1 : D Н G определяется функцией (11). Далее будем предполагать, что функции эйконала на апертуре G и в области фокусировки D связаны соотношениями:

Ф ( и ) = max ( т( x ) -р ( и , x ) ) ,

■ D I А 1                         (13)

Т ( x ) = min ( Ф ( и ) + р ( и , x ) ) .

u ∈ G

При этом оба экстремума в (13) достигаются, когда и и x связаны соотношением x = у _Ф( и ) ( и = Y^- >1 ( x ) = Y_T ( x )). Из уравнений в (13) легко получить, что функция эйконала Ф ( и ) является «огибающей сверху», поскольку для любой функции эйконала линзы Ф l ( и ; x ), входящей в семейство (6), выполняется условие Ф ( и ) > Ф i ( и ; x ).

Отметим, что функции Ф ( и ) и Т ( x ) связаны неравенством Т ( x ) - Ф ( x ) < р ( и , x ) которое превращается в равенство в случае, когда и и x связаны соотношением Y _Ф ( и ) = x . Это позволяет переопределить отображение Y _Ф следующим образом:

Y Ф ( и ) = { x е D | Т ( x ) -Ф ( и ) = р ( и , x ) } . (14)

Обобщим понятие решения исходной задачи формирования заданного распределения освещённости E ( x ), x е D , не предполагая дифференцируемости функции Ф ( и ) и Т ( x ).

Определение 1. «Хорошей парой» будем называть пару функций ( а ( и ), в ( x )), таких что а ( и ) - непрерывна на G , в ( x ) — непрерывна на D , и функции а ( и ) и в ( x ) связаны соотношениями

а(и) = max {в (x) - р (и, x)}, x∈D в (x) =min {а( и) + р (и, x)}. u∈G

Отметим, что на функции а ( и ) и в ( x ) не накладывается требование дифференцируемости. При этом в ( x )- а ( и ) <р ( и , x ) V и е G , V x е D . В приложении 1 показано, что функции а ( и ) , в ( x ) являются липшицевы-ми в областях G и D соответственно. Согласно теореме Радемахера липшицева функция в области является дифференцируемой почти всюду в данной области (то есть мера множества точек, в которых функция не дифференцируема, равна нулю). Значит, для хорошей пары функции а ( и ) и в ( x ) почти всюду дифференцируемы и соответствующее отображение Y _Ф (см. (14)) однозначно в точках дифференцируемости.

Теперь сформулируем, что следует понимать под слабым (обобщённым) решением.

Определение 2. Слабым решением называется «хорошая пара» функций (Ф ( и ), Т ( x )), удовлетворяющая условию сохранения энергии (3) для отображения, определённого формулой (14).

непре-

Отметим, что в слабом решении производные функции Ф ( и ) и, соответственно, отображение (1) определены почти всюду. При этом множество точек недифференцируемости не влияет на величину интегралов в (3).

3.    Вариационная формулировка задачи

Задача поиска слабого решения, рассмотренного в параграфе 2, может быть сформулирована как вариационная задача. Рассмотрим множество пар рывных функций

Q = {(а, в) е C(G) х C(D)| в (x) - а(и) < р(и, x) Vи е G, Vx е D}.

Определим на Q следующий функционал

I ( а , в ) = | в ( x ) E ( x )d x - J а ( и ) E ₀( и )d и .

DG

Очевидно, что I ( а , в ) является непрерывным относительно нормы ||( а , в )|1 о =max{|| а |k,|| 0 |k}, где норма ||-|| _к определяется как максимум модуля функции по всей области.

Теорема 1. Следующие условия эквивалентны:

• 1)    Пара (Ф, Т ) является слабым решением.

• 2)    Пара (Ф, Т ) максимизирует функционал (17).

Доказательство теоремы приведено в приложении 2.

В дискретном варианте задача максимизации функционала (17) может быть записана как задача линейного программирования (ЗЛП). Действительно, возьмём наборы точек { u_i е G } i =f ^ и { x j е D } j =f M , являющиеся узлами прямоугольных решёток Л и © на G и D . Обозначим е ⁰ и e j средние значения функций E ₀( и ) и E ( x ) в ячейках решёток. Кроме того, обозначим р у = р ( u_i , x j ). В результате е ⁰, e j , р ^ - известные числа, а а i = а ( u_i ), в j = в ( x j ) - неизвестные переменные.

В дискретном варианте задача максимизации функционала (17) на множестве Q сводится к следующей ЗЛП:

MN

• I^{Л ,@}(аi, вi) = ^в jej | т j | -^аi-ei⁰ | Ti Н max, j=1             i=1                     ⁽¹⁸⁾

• вj    -аi <ру,i = 1,...,N, j = 1,...,M,

4.    Связь с задачей перемещения масс

где | т j |, | т i | - площади соответствующих ячеек решёток. Отметим, что функция I ^Л , © ( а i , в i ) в (18) соответствует интегральной сумме для непрерывного функционала (17). Естественно ожидать, что при измельчении решёток решения дискретной задачи (18) сходятся к решению исходной непрерывной задачи. Отметим, что матрица ограничений для ЗЛП (18) имеет специфический вид: элементы матрицы принимают значения 0 или ±1. Для решения таких ЗЛП существуют алгоритмы с полиномиальной сложностью [16].

Рассмотрим связь вариационной задачи максимизации функционала (17) с транспортной задачей пе- ремещения массы из области G в область D с функцией стоимости ρ (u, x). При этом распределения масс в областях описываются функциями E0(u), u∈G и E(x), x∈D.

Планом будем называть отображение P : G → D , сохраняющее энергию (меру), то есть для любого измеримого подмножества ω ⊂ G выполнено

∫ E 0 ( u )d u = ∫ E ( x )d x . (19)

P ^{- 1} ( ω ) ω

Допустимо, чтобы отображение P ( u ) было определено почти всюду. Определим функционал на множестве планов

C ( P ) = ∫ ρ ( u , P ( u ) ) E 0 ( u )d u . (20) G

Теорема 2. Пусть (Ф, Ψ ) — слабое решение проблемы. Тогда отображение γ Ф минимизирует функционал (20). Более того, если P – другой оптимальный план, то он совпадает с γ Ф почти всюду.

Доказательство теоремы приведено в приложении 3.

Теорема 2 представляет интересный результат, который может быть рассмотрен как обобщение принципа Ферма. Действительно, среди всех отображений G → D , сохраняющих энергию, слабое решение обратной задачи расчёта эйконала Ф( u ) соответствует отображению, для которого минимизируется суммарное расстояние с весом E 0 ( u ) между точками областей G и D .

Рассмотрим расчёт функции эйконала Ф( u ) по отображению x = γ Ф ( u ) . Для реализации отображения γ Ф ( u ) частные производные функции Ф( u ), определяющие направление лучей, должны иметь вид:

∇ Φ= ( Φ u , Φ u ) = ^{x - u} .                   (21)

^{1     2}      ρ ( u , x )

Функция эйконала может быть восстановлена по своим частным производным на основе следующей известной формулы:

Φ(u1,u2)=Φ(0,0)+

u 1 u 2

+ ∫ Φ u ₁ ( t ,0 ) d t + ∫ Φ u ₂ ( u 1 , s ) d s 00

Действительно, в силу определения слабого решения (см. параграф 2) функция Ф( u ), u ∈ G является липшицевой. Несложно показать, что функция Ф( u ) будет также липшицевой вдоль любой кривой u ( τ ) с натуральной параметризацией. Таким образом, функция F ( τ ) = Ф( u ( τ )) является абсолютно непрерывной функцией натурального параметра τ . В силу свойств абсолютно непрерывных функций функция F ( τ ) однозначно восстанавливается по своей производной, существующей почти всюду, интегрированием вдоль кривой. В частном случае, когда кривая u ( τ ) является ломаной со звеньями, параллельными осям координат, приходим к формуле восстановления (22).

В дискретном варианте задача перемещения масс может быть сформулирована как линейная задача о назначениях (ЛЗН) [19]. Действительно, предположим, что области G и D разбиты на N ячеек (или аппроксимированы N ячейками) с одинаковой энергией, то есть для любой пары ячеек gi ⊂ G, dj ⊂ D выполняется равенство

∫ E 0 ( u )d u = ∫ E ( x )d x = e .

g i d j

В этом случае все отображения G → D , сохраняющие энергию, можно описать перестановками из N чисел ( i 1 , ..., i N ), которые определяют, в какие ячейки d j области D отображаются ячейки g 1 , ..., g N . В рамках ЛЗН отображение ячейки g i в d j можно интерпретировать как выполнение i -м работником j -й работы. Согласно (21), стоимость работ описывается матрицей C i,j = ρ ( u i , x j ), i , j = 1, ..., N , где u i , x j – центры ячеек g i в d j . Таким образом, для численного построения отображения γ Ф , соответствующего слабому решению, можно решать следующую задачу о назначениях

C ( j 1 , , j N ) = ∑ ρ ( u i , x j_i ) → min,               (23)

i где минимум вычисляется по всем перестановкам j1, ..., jN. Для решения ЛЗН предложены эффективные алгоритмы, решающие задачу за полиномиальное время [19].

5.    Расчётные примеры

Рассмотрим задачу расчёта функции эйконала из условия фокусировки пучка круглого сечения с постоянной освещённостью в прямоугольник с постоянной освещённостью. Расчёт проведём для следующих параметров: радиус пучка (радиус области G ) R =3 мм, расстояние до плоскости фокусировки f =50 мм, размер сторон прямоугольника (области D ) d_{x 1} = 12 мм, d x ₂ =4 мм. В силу симметрии задачи, функцию эйконала достаточно рассчитать в первом квадранте из условия фокусировки в прямоугольник D 1 6×2 мм², являющийся одной четвёртой частью прямоугольника D, расположенной в первом квадранте. Для записи ЗЛП (19) были взяты прямоугольные решётки Λ и Θ на G и D с размерами ячеек 0,23×0,23 мм² и 0,375×0,222 мм². В этом случае функция Ф( u ) в первом квадранте и функция Ψ ( x ) в прямоугольнике D ₁ представляются в узлах решёток наборами из N = M = 144 значений. ЗЛП в данном случае содержит 288 переменных и N ²=20736 ограничений-неравенств. Для решения ЗЛП использовалась программа linprog.m из библиотеки Matlab. Рассчитанная функция эйконала Ф ( u ) приведена на рис. 2.

По эйконалу Ф (u) может быть рассчитан преломляющий оптический элемент, расположенный непосредственно перед плоскостью z =0 и формирующий данное распределение эйконала в области G. Рассмотрим плоский освещающий пучок, распространяющийся в направлении оси z. В качестве первой поверхности оптического элемента будем использовать плоскую поверхность, перпендикулярную падающему пучку. Вторая поверхность может быть рассчитана из условия формирования заданного эй- конала в области G плоскости z =0 с использованием принципа Ферма [14]. В то же время при указанных «параксиальных параметрах» высота преломляющей поверхности может быть рассчитана в приближении тонкого оптического элемента [13]:

z ( u ) = Φ ( u ) /( n - 1),

где n – показатель преломления материала оптического элемента.

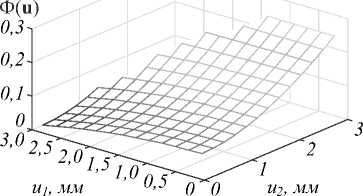
Рис. 2. Функция эйконала в первом квадранте, рассчитанная на основе решения ЗЛП

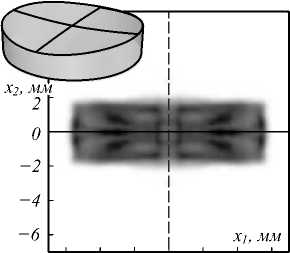
Для проверки правильности полученных в работе теоретических результатов, по функции эйконала Ф( u ) на рис. 2 была рассчитана преломляющая поверхность (24) и затем было проведено моделирование работы полученного оптического элемента в программе для светотехнических расчётов TracePro® с использованием метода трассировки лучей [20]. Для этого поверхность (24) была аппроксимирована системой неоднородных рациональных сплайнов Безье (NURBS) в программе автоматизированного проектирования Rhinoceros® [21]. На рис. 3 показаны преломляющий оптический элемент ( n = 1,5) и рассчитанное в программе TracePro распределение освещённости, которое формируется при освещении оптического элемента коллимированным пучком с постоянной освещённостью.

Рис. 3 а , б показывают фокусировку в прямоугольник заданного размера. Среднеквадратическое отклонение (СКО) полученного распределения освещённости от постоянного значения составляет 16,2%. Неравномерность распределения энергии в точках фокусировки объясняется недостаточным числом точек N = 144, использованным для представления функции эйконала (рис. 2). В то же время увеличение числа точек N приводит к сильному увеличению вычислительной сложности ЗЛП, поскольку размерность матрицы ограничений, определяющая сложность задачи, равна N ². Время решения ЗЛП для N = 144 на стандартном персональном компьютере (Intel® Core™ i7-2600 CPU @3.4 GHz) составило около 5 часов.

Существенно более эффективный метод решения задачи состоит в расчёте отображения x = γ Ф ( u ) с использованием ЛЗН (24). Для расчёта отображения γ Ф в рамках той же задачи фокусировки апертура G была аппроксимирована набором из N = 1060 квадратных ячеек g i с размером 0,162×0,162 мм². Прямоугольник D также был представлен в виде объединения N = 1060 прямоугольных ячеек d i с размером 0,231×0,21 мм² .

а)     -6 -4 -2 0 2 4 6

1.0

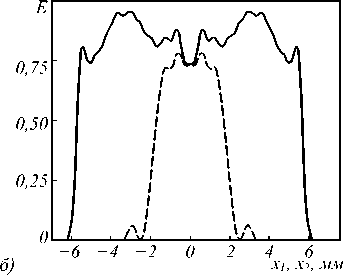
Рис. 3. Оптический элемент для фокусировки пучка круглого сечения в прямоугольник 12×4 мм2, рассчитанный на основе решения ЗЛП. Формируемое распределение освещённости (а) и сечения распределения освещённости по осям координат (б)

Для решения ЛЗН использовалась программа munkres.m [22], реализующая венгерский алгоритм в среде Matlab [19]. В этом случае время решения ЛЗН при прочих равных условиях составило менее одной секунды. По рассчитанному отображению по формуле (21) были вычислены производные функции эйконала, и затем по формуле (22) была восстановлена функция эйконала численным интегрированием. Далее с использованием (24) был построен оптический элемент, фокусирующий в прямоугольник. Полученный оптический элемент и рассчитанное в программе TracePro распределение освещённости, формируемое оптическим элементом, приведено на рис. 4. В отличие от рис. 3, распределение освещённости на рис. 4 является значительно более равномерным, СКО полученного распределения освещённости от постоянного значения составляет всего 5,6%.

Представленные примеры показывают, что расчёт функции эйконала на основе решения ЛЗН (23) является оптимальным как с точки зрения времени расчёта, так и качества формируемого распределения.

Заключение

В работе показано, что задача расчёта функции эйконала из условия фокусировки в заданную область может быть сформулирована как вариационная задача максимизации функционала (17) и как задача Монжа–Канторовича о перемещении масс. Получено, что функция стоимости в задаче Монжа–Канторовича соответствует расстоянию между точкой области задания эйконала и точкой области фокусировки.

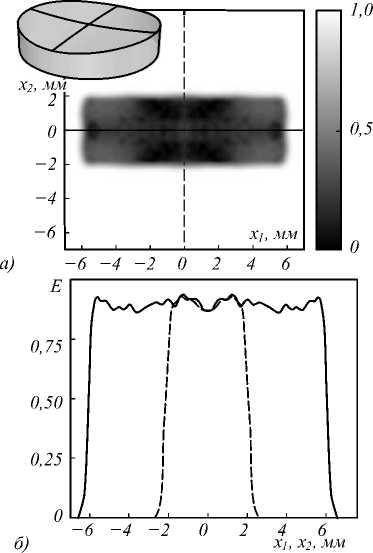
Рис. 4. Оптический элемент для фокусировки пучка круглого сечения в прямоугольник 12×4 мм2, рассчитанный на основе решения ЛЗН. Формируемое распределение освещённости (а) и сечения распределения освещённости по осям координат (б)

Данный результат показывает, что решение обратной задачи расчёта эйконала соответствует отображению, для которого минимизируется суммарное расстояние между точками исходной плоскости и области фокусировки. Предложенный в работе формализм позволил свести расчёт функции эйконала к решению ЗЛП (18). При этом расчёт отображения, соответствующего функции эйконала, сводится к решению ЛЗН (23). Представленные примеры расчёта оптических элементов показывают, что метод расчёта эйконала на основе решения ЛЗН (23) требует существенно меньших вычислительных затрат по сравнению с методом на основе решения ЗЛП (18).

Отметим, что подход, основанный на использовании ЛЗН, может быть также использован для расчёта зеркал, формирующих заданные распределения интенсивности. Отличие состоит только в виде функции стоимости [11, 15]. С точки зрения вычислительных затрат данный подход является существенно более эффективным, чем расчёт зеркал на основе решения ЗЛП, рассмотренный в [17, 18].

Работа выполнена при поддержке гранта РФФИ 1807-00982 в части формулировки и решения указанной задачи как задачи о перемещении масс с использованием линейной задачи о назначениях и при поддержке Федерального агентства научных организаций (соглашение № 007-ГЗ/Ч3363/26) в части вариационной формулировки обратной задачи расчёта функции эйконала из условия фокусировки в заданную область.