Вариант нелинейной модели течения тиксотропных вязкоупругопластических сред со степенной зависимостью вязкости и модуля сдвига от текущей структурированности

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2024PNRPU MECHANICS BULLETIN

Исследование и адекватное моделирование нелинейных реологических эффектов, в частности тиксотропии, изучение механизмов, их порождающих, и построение определяющих соотношений (ОС) течения неньютоновских вязких жидкостей и вязкоупругопластичных сред (например, суспензий, эмульсий, гелей, полимеров в вязкотекучем состоянии или в виде расплавов и растворов, битумов и их модификаций минеральными и эластомерными наполнителями, металлов и сплавов в состоянии сверхпластичности и т.п.) с учетом происходящих в них структурных изменений важны для понимания закономерностей и моделирования огромного количества природных и технологических процессов [1–53]: движения магмы, поведения грунтов, схода селей и лавин, разнообразных технологий переработки полимеров [15–20] и других материалов (экструзии волокон, прессования, штамповки, 3D-печати заготовок полимерами, металлическими дисперсиями, C-SiC пастами и т.п.) [18; 20–23], нефтедобычи и перекачки водонефтяных эмульсий, дорожного строительства, производства лаков, красок, масел, пищевых продуктов, гемодинамики и медицинской микрофлюидики [24–26]. Например, в полимерных системах эволюция структуры (разнообразных связей между макромолекулами и надмолекулярными агрегатами на разных уровнях иерархии), влияющая на физико-механические свой- ства, обусловлена, прежде всего, огромной длиной и сложной формой макромолекул, их гибкостью, многочисленными степенями свободы их сегментов, наличием межмолекулярных взаимодействий, приводящих к образованию (и разрушению) зацеплений, узлов, водородных связей, сшивок, кристаллитов и других элементов иерархической пространственной структуры [3–7; 9; 12; 14–19; 27–29]. Моделирование течения полимерных систем традиционно опирается на макроскопическую феноменологию и аппарат механики стабильных сплошных сред и в лучшем случае учитывает лишь влияние изменения фазового состава и структуры среды (скорости полимеризации, кристаллизации, гелеобразования и т.п.) на характер течения, но не учитывает (из-за сложности) влияние деформирования на кинетику изменения структуры [3–7; 9–17; 19; 30]. Основные наблюдаемые у неньютоновских жидкостей реологические эффекты - возрастание кривой течения т = F(Y), зависимость вязкости среды п от скорости сдвига a = у или от напряжения τ («аномалия вязкости», так как у ньютоновской жидкости вязкость не зависит от а и τ), температуры и давления [1–20; 31–37], существование конечных пределов вязкости при а ^ 0 и а ^ ^ (максимальной и минимальной Ньютоновых вязкостей) [1– 20; 31–37], сверханомалия вязкости (наличие участка убывания на кривой течения) [34; 35; 40; 42], разбухание экструдата на выходе из канала фильеры (эффект

Баруса) [3; 4; 6; 10; 14–19], тиксотропия (обратимое разрушение структуры, вызывающее уменьшение вязкости с ростом скорости деформации или под действием постоянного напряжения, превышающего некоторый порог, с последующим ее восстановлением после снятия воздействия) [19–30] и др. Типичные кривые вязкости разных псевдопластических сред приведены на рис. 1, 2 (и рис. 8, 9).

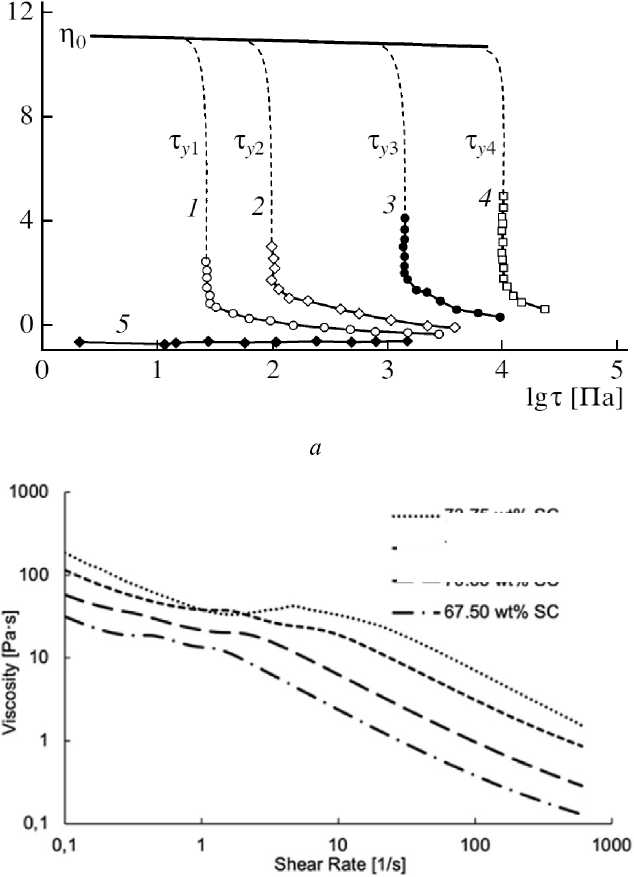
На рис. 1, а , приведены кривые вязкости полиизобутилена (эластомер, термопласт) наполненного высокодисперсным техническим углеродом (кривые 1–4 – с 2,5; 5; 9 и 13 об.% углерода, 5 – чистый полиизобутилен) [27], а на рис. 1, b – кривые вязкости C–SiC паст (многокомпонентных суспензий) для печати зеленых заготовок керамических изделий с разным содержанием твердых наполнителей (порошков углерода и карбида кремния) при 20 °С [23].

lgr| [Па с]

b

Рис. 1. Кривые вязкости: а – суспензий технического углерода в полиизобутилене (нанокомпозита) с разным содержанием углерода, b – C–SiC паст для печати зеленых заготовок керамических изделий с разным содержанием твердых наполнителей (порошков углерода и карбида кремния) при 20 °С

73.75 Wt% SC

-----72.50 wt% SC

--70.00 wt%SC

• Fig. 1.    Viscosity curves: a – suspensions of carbon black in polyisobutylene (nanocomposite) with different carbon contents; b – C–SiC pastes for printing green blanks of ceramic products with different contents of solid fillers (carbon powders and silicon carbide) at 20 °C

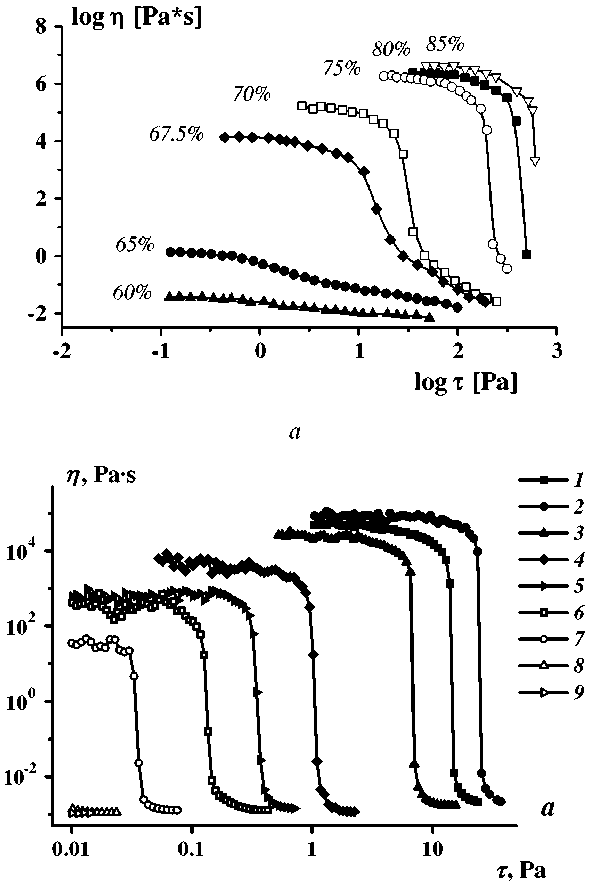
На рис. 2, а приведены кривые вязкости эмульсий «вода – циклометикон (кремнийорганическое масло)» с разным содержанием дисперсной фазы, а на рис. 2, b – кривые вязкости разбавленных коллоидных систем (гелей) серебро-цистеин (аминокислота): кривая 1 – для геля с 0,036 мас.% дисперсной фазы, кривые 2–9 – для геля разбавленного в 2 n - 1 раз [28].

b

Рис. 2. Кривые вязкости эмульсий «вода – циклометикон» с разным содержание масла ( а ); кривые вязкости разбавленных коллоидных систем (гелей) «серебро – цистеин» ( b ): кривая 1 – для геля с 0,036 мас.% дисперсной фазы, кривые 2–9 – для геля разбавленного в 2 ^{n –1} раз

• Fig. 2.    Viscosity curves of water-cyclomethicone emulsions with different oil contents ( a ), viscosity curves of diluted silver-cysteine colloidal systems (gels) ( b ): curve 1) for a gel with 0.036 wt.% dispersed phase, curves 2–9 ) for a gel diluted 2 ^{n –1} times

Обычно для аппроксимации возрастающей кривой течения среды используют простейший степенной закон т = nYn, n > 0 • Поскольку такая зависимость не распространяется на весь диапазон скоростей сдвига, а начальная кажущаяся вязкость т / у равна бесконечности при n < 1 (для псевдопластических жидкостей) или нулю при n > 1 (для дилатантных), то за полтора столетия, начиная с работ Максвелла, Шведова, Бингама, Оствальда, Олдройда, Лоджа, предложено более сотни разных феноменологических и структурных определя- ющих соотношений (реологических моделей), аппроксимирующих нелинейные зависимости напряжения (или вязкости) от скорости сдвига разных сред в определенном интервале скоростей сдвига [1–21; 26; 30; 31– 50]: модели Шведова – Бингама [1], Гершеля – Балкли, Кэссона, Кросса, Кригера, Джиллеспи [20; 30; 45; 46], Бернштейна – Кирсли – Запаса (BKZ) [20; 30; 46], Ол-дройда [31], Лоджа [3], Леонова – Прокунина [7; 33; 38], Карро – Ясуда [11; 19; 20; 30], Виноградова – Покровского [4; 19; 43] и ее обобщение [43; 50], Гиезекуса [36], Менцера, Фан-Тьен – Тэннера [13; 19], «Pom-Pom»-модели [11; 39] и др. Большинство моделей носят феноменологический характер, содержат подгоночные параметры, не имеющие определенного физического смысла, не учитывают упругость жидких сред и эволюцию их микроструктуры. Лишь немногие из сотни известных ОС жидких сред учитывают не только их вязкость и пластичность, но и вязкоупругость (столь характерную, например, для расплавов и концентрированных растворов полимеров, для жидкостей-пропантоносителей и т.п.), и так или иначе – процессы формирования и разрушения структуры; последняя в большинстве случаев описывается всего одним структурным параметром [3; 6; 10; 19; 20; 30; 45; 46; 48–53]. Представляется необходимым адекватно моделировать взаимное влияние этих процессов, особенности их конкуренции и эпифеномены их взаимодействия, в частности возрастание кривой течения, зависимость вязкости среды от скорости сдвига («аномалию вязкости»), температуры и давления, существование конечного предела вязкости при стремлении скорости к нулю или к бесконечности (максимальной и минимальной ньютоновских вязкостей) и тиксотропию [19–30].

Цель данной статьи – формулировка и анализ нового варианта ОС для описания сдвигового течения тиксотропных вязкоупругопластичных сред, исследованного автором в работах [54–60], и доказательство того, что он наследует основные обнаруженные полезные свойства первого варианта ОС, но дает дополнительные инструменты для моделирования, поскольку эволюция времени релаксации модели и ряд качественных свойств фазовых кривых и кривых течения и вязкости отличаются.

1. Варианты модели течения тиксотропных сред с эволюцией структуры

Данная статья – продолжение цикла работ [54–60], посвященных системному аналитическому исследованию одноосного прототипа нелинейного ОС для описания изотермического сдвигового течения тиксотропных вязкоупругопластических сред, учитывающего взаимное влияние процессов деформирования и эволюции структуры (кинетики ее образования и разрушения):

Y = Т / G + т / n , n = n( w ), G = G ( w ), (1)

П( w ) = n o e^a w , G ( w ) = G о e ^в w , П о , G 0 >  0, 0 <  в <  a, (2) w = k 1 (1 - w ) - k ₂ g ( s ) w ,              (3)

и изучению порождаемых ОС (1)–(3) кривых течения, вязкости, деформирования, релаксации и ползучести [57–60]. В основу ОС (1)–(3) положена нелинейная модель Максвелла, в которой τ – касательное напряжение, γ( t ) – угол сдвига, а модуль сдвига G и динамическая вязкость η зависят от изменения структуры полимера под влиянием деформирования, т.е. от безразмерного структурного параметра w ( t ) (степени структурированности): G = G ( w ), n = n( w ), w ( t ) ^e [0;1]. ОС (1)—(3) управляется шестью материальными параметрами (МП) k 1 , k ₂, n₀, G₀, a >  0, в >  0 и одной неубывающей материальной функцией (МФ) g ( s ). Кинетика изменения w ( t ) задается уравнением вида (3), учитывающим зависимость скорости разрушения структуры от безразмерного напряжения s = т( t )/т c (т c - некоторое характерное касательное напряжение) посредством МФ g ( s ), s >  0 (см. подробнее в [54–60] и ниже). Вообще говоря, модуль сдвига G и вязкость η зависят еще и от температуры, давления и скорости сдвига v (градиента скорости), но температуру, давление и скорость (простого) сдвига Y = v (в этой работе) мы пока считаем постоянными. Таким образом, ОС (1)–(3) относится к классу ОС с внутренними переменными. Под w ( t ), как подробнее объяснено в [56–58], можно понимать, например, степень сшитости или степень кристалличности полимера (поскольку их кинетику можно описать дифференциальным уравнением вида (3)), изменения в среднем размере, форме и ориентации частиц фаз в суспензиях, эмульсиях, полимерных системах и зерен в пластичных поликристаллических металлах и сплавах, пористость, образование, рост и разрушение агрегатов, кристаллитов или зерен, образование Ван-дер-Ваальсовых связей и сшивок между молекулами золей или растворов полимеров, в частности отношение концентрации надмолекулярных или межмолекулярных связей (зацеплений, водородных связей, сшивок и т.п.) в текущий момент времени к некоторому максимально возможному значению концентрации связей для данной температуры.

Функции п = n( w ) и G = G ( w ) в (1) должны быть неубывающими. В [54–60] они задавались в виде экспонент (2), следуя традициям кинетики, а в этой работе изучим модель со степенными зависимостями:

П( w ) = П 0 w ^a, G ( w ) = G 0 w ^в, П 0 , G 0 >  0, 0 <  в <  a, (4)

(обозначения параметров унаследованы от (2) для удобства сравнения). Поскольку вязкость обычно сильнее зависит от структурированности, чем модуль сдвига, то в <  a, как и в (1)-(3). Время релаксации модели Максвелла T = n / G выражается формулой T ( w ) = T₀ w ^{a - e},

T₀ = П о / G ₀; условие в <  а равносильно постулированию возрастания функции T ( w ). Параметры G ₀ и п₀ в (4) задают максимальные модуль сдвига и вязкость при w = 1; можно положить в = 0 , чтобы пренебречь зависимостью G ( w ). При w ч 0 вязкость, модуль сдвига и время релаксации стремятся к нулю, т.е. в пределе модель (1), (3), (4) описывает жидкость с очень низкими структурированностью, вязкостью и модулем сдвига (ниже будет доказано, что равновесное время релаксации T * , т.е. предел T ( w ( t )) при t ч^ , убывает с ростом скорости сдвига v и T * ч 0 при v ч^ ) - в отличие от первого варианта модели (1)-(3), у которого T ( w ) >  T ₀, T (0 + ) = T ₀ >  0 и T * ч T₀.

Задача данной статьи - аналитическое исследование общих математических свойств (при произвольных шести МП и МФ g ( s )) нового варианта модели (1), (3), (4). Модель (1), (3), (4) будет сведена к задаче Коши для системы двух нелинейных дифференциальных уравнений для (безразмерных) касательного напряжения s ( t ) и структурированности w ( t ), будет проведен анализ зависимости (единственного) положения равновесия системы (равновесных напряжения и структурированности) от скорости сдвига, всех МП и произвольной МФ, вывод уравнения кривой течения и кривой вязкости модели, изучение поведения интегральных кривых и фазового портрета нелинейной системы двух дифференциальных уравнений для s ( t ) и w ( t ) в окрестности положения равновесия. Будет доказано, что все полезные базовые свойства модели (1)-(3) и ее способность описывать основные реологические эффекты, обнаруженные в [54-60], сохраняются, но выбор степенных зависимостей (4) (вместо (2)) приводит к ряду существенных качественных изменений в поведении кривых модели и позволяет описывать немного иной класс сред, у которых основные реологические эффекты проявляются в иной форме. И поэтому новый вариант модели полезен как дополнение инструментария для моделирования течения разнообразных тиксотропных сред. В дальнейшем будут исследованы кривые деформирования, релаксации, ползучести и восстановления, порождаемые ОС (1), (3), (4), и другие аспекты его способности описывать не только жидкообразные, но и твердообразные (густеющие, твердеющие, отвердевшие) материалы (по аналогии с [57-60]). Обоснование актуальности темы исследования, подробный литературный обзор и сферы приложений приведены в работах [56; 58; 60].

Об уравнении эволюции структурированности и материальной функции модели

В уравнение (1) входят две искомые функции т( t) и w (t), и необходимо добавить некоторое кинетическое уравнение (3), описывающее эволюцию структурированности среды w (t) и учитывающее влияние напряжения (или иных характеристик процесса деформирования). Уравнение (3) отражает представление о том, что структурированность меняется в результате борьбы двух основных процессов: разрушения «сшивок» (структурных связей) и образования новых. С ростом напряжения разрушение (т.е. убывание w(t)) ускоряется, вязкость падает, а скорость образования новых сшивок можем считать постоянной (в первом приближении, при фиксированной температуре) и пропорциональной плотности возможных, но не реализованных сшивок (1-w). Поэтому уравнение для w(t) можно принять в виде (3), где k1, к2 > 0 - МП (зависящие от температуры), задающие скорости образования и разрушения сшивок, а g(s), s > 0, - неотрицательная возрастающая (нестрого) кусочно-гладкая функция, такая, что g (0) = 1 и g(+“) = +^ (роль этого ограничения указана в [5456]), задающая зависимость скорости разрушения сшивок от безразмерного напряжения s = т(t)/тc (тc - некоторое характерное касательное напряжение: пороговое, предельное или тc = 0.01G0). Допустим, случай g(s) = 1 при s е [0; sj. Например, в [56-60] для иллюстраций использованы МФ вида

g ^{( s} ) = e h , g ^{( s} ) = ^{1 + ( hs )2}, g ^{( s} ) = ^{1 + hs} ,        (5)

g = 1 + ln(1 + hs ), h >  0.

Таким образом, в моделях (1)-(3) и (1), (3), (4) учитывается кинетика взаимосвязанного протекания двух сопряженных процессов: сдвигового течения и изменений структуры материала: в уравнении (1) вязкость и модуль упругости зависят от структурированности (характеристика второго процесса), а скорости разрушения и восстановления структуры зависят от напряжения (характеристики первого процесса). Важное отличие выбранной формы уравнения (3) - постулирование зависимости МФ g и скорости разрушения структуры именно от напряжения, а не от скорости сдвига (в отличие от 95-98 % всех ОС сред, учитывающих изменение структуры). Оказывается, что базовые свойства этих двух классов ОС, опирающихся на модель Максвелла (1), и их возможности по описанию реологических эффектов (типичных качественных свойств кривых течения, вязкости, деформирования, ползучести и релаксации) сильно различаются. Самые важные отличия: 1) у моделей, в которых скорость разрушения структуры зависит от скорости сдвига точка равновесия, - всегда узел и не может быть фокусом, как у ОС (1)-(3) [56;57] и (1), (3), (4); 2) иные свойства кривых течения, деформирования, ползучести и релаксации. Но анализ этих различий - тема другой статьи.

На данном этапе будем характеризовать текущую структуру материала лишь одним параметром w(t), не различая механизмы влияния разных элементов надмолекулярной структуры на вязкость (или пренебрегая ими); пока будет важно лишь то, что материал имеет структуру, которая разрушается под действием напряжений сдвига и может восстанавливаться. Даже такой простой подход (при условии понимания значимости вкладов в эволюционное уравнения (3) для w(t) разных конкретных механизмов изменения структуры) позволяет описать большое количество наблюдаемых эффектов [54-60]. В дальнейшем модель будет обобщена введением второго структурного параметра, учитывающего механизм ориентирования и распрямления макромолекул (гибкоцепных) полимеров при одноосном деформировании и другие эффекты.

Модель (1)-(3) (после формулировки в трехмерном случае, дальнейшего исследования, детального сопоставления с данными экспериментов и необходимых обобщений, в частности, учета влияния тепловыделения и теплообмена и введения дополнительных структурных параметров и уравнений для учета кинетики основных физико-химических процессов) будет применяться для описания испытаний битумов и их модификаций минеральными и эластомерными наполнителями [6165], расплавов термопластов (полиэтиленов, полиамидов, полифениленсульфида, полиэфирэфиркетона и др.), углеродно-кремниевых паст для 3П-печати зеленых заготовок керамических деталей [22; 23] и для решения краевых задач в технологиях переработки полимеров (в частности, твердофазной плунжерной экструзии, формования нитей методом экструзии расплава и вытяжки) [14-19] и задач моделирования сверхпластического деформирования металлов и сплавов с учетом эволюции нескольких параметров структуры (среднего размера, формы и ориентации зерен, доли большеугловых границ, уровня неравновесности границ зерен, плотности дисперсоидов, степени сегрегации на границах зерен легирующих элементов, облегчающих зернограничное скольжение и т.п.) [66-77]. Модель (1)-(3) будет применяться и для решения задач ползучести с учетом накопления поврежденности и кинетики химических превращений под влиянием агрессивной среды. В этом случае вполне возможно трактовать величину 1 — w как скалярный параметр поврежденности, причем его не только можно считать монотонно возрастающим в процессе ползучести (положив в уравнении (3) k1 = 0 или достаточно малым), когда в силу (4) модуль сдвига и вязкость будут монотонно убывать в процессе ползучести (поврежденность накапливается - материал деградирует), но и учитывать процесс залечивания повре-жденности под влиянием разных факторов (например, под воздействием электрического тока в металлах и сплавах или под воздействием повышенных температур, как происходит в углерод-углеродных композитах, в которых нагрев замедляет и залечивает поврежден-ность, вызванную облучением нейтронами). С целью расширения класса описываемых эффектов и области применимости модели (1)-(3) и (1), (3), (4) удобно использовать как элемент более сложных гибридных моделей в сочетании с физически нелинейным ОС типа Максвелла для структурно-стабильных вязкоупругопластических материалов, исследованным в цикле статей [78-83] и др.

3.    Безразмерные уравнения модели и положение равновесия системы

Введение безразмерного времени t = t/T0 (после упрощения обозначений и замены t на t) дает уравнения модели (1)-(3) в безразмерном виде s = aw — sw (в-“’,                (6)

w = c [(1 — w (1 + bg ( s ))],               (7)

где a = vn0/Tc =vT0G0/tc, b = k2/k1, c = k1T0 - безразмерные материальные параметры (те же, что и для ОС (1)-(3)): а зависит от п0 и заданной скорости сдвига v, а b и c характеризуют борьбу процессов образования и разрушения сшивок и соотношение их скоростей с Т0. К системе (6), (7), конечно, нужно добавить начальные условия w(0) = w0 и s(0) = s0, w0 е (0;1], s0 > 0. Параметр w0 следует рассматривать как еще один МП модели, характеризующий начальное состояние материала, т.е. результат его предыстории (он, конечно, сильно влияет на кривые деформирования, релаксации и ползучести, порождаемые ОС [56-60]). Автономная система двух нелинейных дифференциальных уравнений (6), (7) для s(t) и w(t) удовлетворяет условиям теоремы существования и единственности решений задачи Коши, если МФ g(s) непрерывно дифференцируема при s > 0.

Найдем положения равновесия системы (6), (7), чтобы исследовать его зависимость от материальных параметров, а затем - фазовый портрет системы в его окрестности. Точки равновесия - решения системы уравнений aw ^e — sw ^(в "■’ = 0, c [(1 — w (1 + bg ( s ))] = 0, т.е.

s = aw ^a, w = F ( s ),               (8)

F ( s ) = 1/ B ( s ), B ( s ) = 1 + bg ( s ), s > 0.        (9)

Система (8) зависит лишь от трех параметров a, a = v p₀/T _c , b = k₂/k 1 и от МФ g , но не зависит от c , G₀ , в из (7) и (4) (у модели (1)-(3) второе уравнение (8) такое же). Функция B ( s ) зависит от величины отношения bg ( s ) скорости разрушения сшивок к скорости их образования в уравнении (3), она возрастает (так как МФ g ( s ) возрастает) и всегда B ( s ) >  1 + b >  1 (так как

g ( s ) >  1); F ( s ) - убывающая функция, F (0) = (1 + b ) 1 , F ( s ) ч 0 при s ч ^ , поскольку g ( +^ ) = +^ .

Так как из (8) w = ( s / a )^1/a - возрастающая функция s при s >  0, а F ( s ) убывает, то система (8) имеет не более одного решения, причем для него s e (0; a ], поскольку w e (0;1]. Решение существует, поскольку F (0) e (0;1), F ( “ ) = 0, а область значений непрерывной функции ( s / a )^1/a, s e [0; a ], совпадает с отрезком [0,1]. Итак, при любых МП a , b , a, c , n₀, G 0 >  0 , в >  0 и любой неубывающей МФ g ( s ) решение системы (8) существует и единственно в области w e (0;1) &  s e (0; a ). Обозначим точку равновесия системы (6), (7) через ( s * , w * ), s * = s * ( a , b ,a), w * = w * ( a , b ,a). Из (8) следует система уравнений для s _* , w _* :

s * = aw * ^a , w * = F ( s * ).               (10)

Равновесное напряжение s * = s * ( a , b , a) - единственное решение уравнения

• ( s * / a ) 1/ ^a = F ( s * ), или s * / a = (1 + bg ( s * )) ^{- a}.     (11)

Из (10) и свойств F ( s ) следуют оценки

0 <  F ( a ) <  w * <  1/(1 + b ) <  1, 0 <  aF ( a )^a <  s * <  a (1 + b ) ^a <  a .

Отметим, что для модели (1)–(3) с экспоненциальными η( w ) и G ( w ) всегда выполнялось противоположное неравенство s * ( a ) >  a . Это удобный для проверки по данным испытаний материала индикатор применимости первого или второго вариантов модели.

В силу (10) кривая w = F ( s ), s >  0, в фазовом пространстве {( s , w )| s >  0, w e (0;1]} системы уравнений (6), (7) – геометрическое место точек равновесия; она не зависит от параметра a (от скорости сдвига) и с изменением a , точка равновесия двигается вдоль нее в соответствии с зависимостью s _*( a ). Кроме того, кривая w = F ( s ) - множество точек, в которых поле скоростей системы уравнений (6), (7) параллельно оси s , т.е. w v = 0 в точках пересечения любой фазовой кривой с кривой w = F ( s ) [57]). Функция F ( s ) играет ключевую роль при анализе интегральных кривых, диаграмм деформирования и кривых ползучести обоих вариантов ОС [56–60].

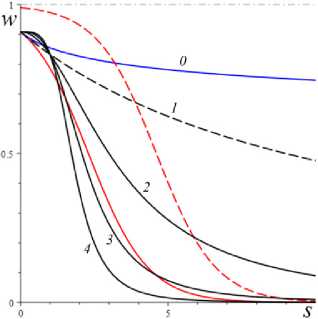
На рис. 3, а, приведены графики функции F(s) (9) для b = 0,1 и разных МФ (5) с h = 1 : логарифмической (кривая 0), четырех степенных g(s) = 1 + (hs)n, n = 1...4 (кривые 1–4) и экспоненциальной МФ (красная кривая). Все графики, кроме 0,1, имеют точку перегиба (для лю- бого n > 1). В пределе при n ч ^ семейство функций F(s;n) сходится к ступеньке F^ = w0[h(s) - h(s -1)] (FL (s) = 0 при s > 1). Для сравнения приведен и график F(s) для b = 0,001 и той же МФ g = eh (красная штриховая линия). На рис. 3, b, приведены графики функций (8) (для разных моделей при разных а), пересечение которых – точка равновесия (s*,w*): черные кривые s = awa с a = 2 и a = 1;3;9; 50; 100; 1000, цветные кривые w = F (s) для девяти моделей с b = 10~6;10-3;10-2 (голубые, синие и красные линии) и с тремя МФ вида (5): g = eh , h = 1 (сплошные линии), g = 1 + (hs)2, h = 1 (штриховые) и g = 1 + hs , h = 10 (пунктирные).

b

Рис. 3. a – графики функции F ( s ) для моделей с b = 0,1 и разными МФ вида (5); b – графики функций (8) при разных а , пересечение которых – точка равновесия ( s _*, w _*)

Fig. 3. a) function graphs F ( s ) for models with с b = 0.1 and different material functions of the type (5); b) graphs of functions (8) for different а , the intersection of which is the equilibrium point ( s _*, w _*)

Формула (11) задает в неявной форме кривую течения s* (a) (или s* (ν)), порождаемую ОС (1)–(3). Из (11) следует зависимость (установившейся) кажущейся вяз- кости ц = t*/v= n0s*/а от равновесного напряжения s* = т*/тc (а также от скорости сдвига v или структурированности w* ), порождаемая ОС (1), (3), (4) (с любыми МП а, b, a, c, n0, G0 > 0, в - 0 и любой неубывающей МФ g(s) - 1) при рассматриваемом режиме деформирования:

ц = n₀ F ( s * )^a , или ц = n₀ w * ^a = n( w * ) (12)

(формулу (12) можно получить и подстановкой w = w * в (4)). Для ОС (1), (3), (4) вязкость – степенная функция от w _* . Характер зависимости µ от параметра a (т.е. от скорости сдвига ν) полностью определяется зависимостью w _* от a (или s _* ( a )) и ниже будет доказано, что кажущаяся вязкость (12) (и w _* ( a )) монотонно убывает по a , как и в случае модели (1)–(3).

Отметим, что для модели (1)–(3) уравнения (6), (8), (10)–(12) другие, в частности точка равновесия – решение системы ln s * / а = a F ( s * ), w * = F ( s * ) (вместо (10)).

Анализ зависимостей точки равновесия и кажущейся вязкости от материальных параметров

Для произвольной неубывающей МФ g ( s ) исследуем характер зависимости функций s * = y ( а , b ,a), w _* ( a , b , α) (они задаются в неявной форме системой двух нелинейных уравнений (10)) и μ( a , b , α) от трех параметров a , b , a >  0. В силу связи In Ц = In s * — In a + In П ₀ (при фиксированной скорости сдвига, когда меняются лишь МП b и α, связь между In Ц и ln s * линейна) производные ln Ц и ln s * по b или a совпадают: ц‘ / ц = s ’ / s * . Поэтому совпадают знаки производных и интервалы монотонности величин µ и s _* по b или по α. Продифференцируем тождество (11), задающее функцию s * = y ( а , b , a ), по b :

Уъ^а - ¹ = ^{— a(1 +} bg ⁽ У ^))—a - ^{1 [} g ⁽ У ) ⁺ bg ^/( У ) У ь ],

Уь [а—1 + aw*a+1 bg‘(y)] = —aw*a+1 g(y), yb = — а aw*a+1 g (y) / (1 + abaw*a+1 g'(y)) < 0

(в силу g'(s) - 0 и положительности МП и функции s* = y(а,b,a)). Поэтому s* = y(а,b,a) убывает по b на всей полуоси b > 0 . В силу связи w* = (s*/а)1/a функция w* = w*(а, b, a) тоже убывает по b на интервале b > 0 . Таким образом, равновесные напряжение s* , кажущаяся вязкость (12) и структурированность w* монотонно убывают по параметру b. При b ^ 0 + w* ^ 1 и s* ^ а, а при b ^ +^ w* ^ 0 (как у исходной модели (1)-(3)) и s* ^ 0, т.е. для любых а,a график s*(b) имеет горизонтальную асимптоту s* = 0 при b ^ +^ (в отличие от модели (1)–(3), у которой s*(b) имеет асимптоту s* = а , зависящую от скорости сдвига [56]). Так как s* = aw*a , то при фиксированных МП а и a МФ не влияет на зависимость s*(w*), а множества точек кривых Саа = {(s*(b), w*(b)) | b > 0} в фазовом пространстве не зависят от МФ g.

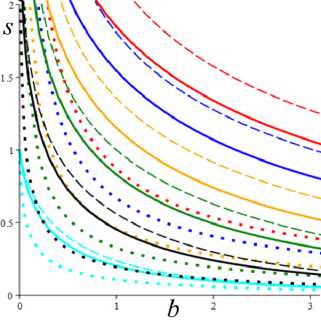
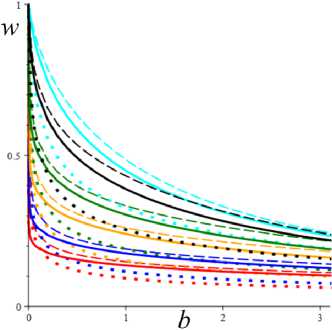
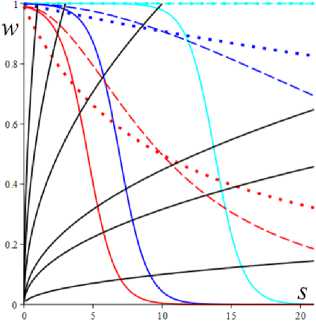
Рис. 4. Графики зависимостей координат положения равновесия s * ( b ) и w * ( b ) для трех моделей с a = 2 и МФ (5) (сплошные, штриховые и пунктирные линии соответственно) при шести скоростях сдвига: а = 1; 3; 9; 20; 50; 100 (голубые, черные, зеленые, желтые, синие и красные кривые)

Fig. 4. Graphs of the dependences of the equilibrium position coordinates s * ( b ) and w * ( b ) for three models with a = 2 and material function (5) (solid, dashed and dotted lines, respectively) at six shear rates: а = 1; 3; 9; 20; 50; 100 (blue, black, green, yellow, blue and red curves)

На рис. 4 приведены графики зависимостей равновесных напряжения и структурированности s*(b) и w* (b), порожденные моделями с a = 2 и тремя МФ вида (5): g = ehs с h = 1 (сплошные линии), g = 1 + (hs)2 с h = 1 (штриховые ) и g = 1 + hs с h = 10 (пунктир- ные). Для каждой из трех моделей рассмотрены шесть разных скоростей сдвига: a = 1; 3; 9; 20; 50; 100 (голубые, черные, зеленые, желтые, синие и красные кривые).

Дифференцируя второе уравнение (10) по α (или по a , или по любому параметру, кроме b ), получим w * _a = - b (1 + bg ( s * )) ^{— 2} g '( s * ) s * _a. Поэтому sgn w * _a =— sgn s * _a , т.е. интервалы монотонности величин w _* и s _* по α (или a ) совпадают, возрастание s _* влечет убывание w _* , а убывание s _* – возрастание w _* . Производная (11) по α (α не входит в определение F ( s )):

ya /a = F(y)a [In F(y) + a F(yY1 F'(y)ya ], ya (1 — aw“a w—1F'(y)) = aw“ In w*, (т.к. F(y) = w*) и y a = aw* In w*/(1 — a a w*a—1F'(y)) < 0, (13) при a > 0, так как F'(y) < 0 и In w* < 0 . Поэтому s* = y(a, b, a) убывает по a, а w*(a, b, a) возрастает по a. Стационарное значение вязкости (12) тоже убывает по α при любых МП и МФ (в отличие от модели (1)–(3)), ибо выше было показано, что ца /ц = ya/y, т.е. ца = n0ya /a . У модели (1)-(3) функции s*(α) и μ(α) , наоборот, возрастают, а w*(α) убывает [31; 33].

Найдем пределы s * и w * при a ^ + 0 и a ^ ^ (они существуют в силу монотонности функций, а оба предела w * (a) конечны и лежат в отрезке [ F ( a ); 1/(1 + b )], так как F ( a ) <  w * <  1/(1 + b )). Перейдем к пределу при a ^+ 0 в тождестве (10): из w * (0 + ) >  0 следует, что s * (0 + ) = a ; тогда в силу второго уравнения (10) w * (0 + ) = (1 + bg ( a )) ^{— 1} и inf w * (a) = w * (0 + ). Переход к пределу при a ^^ в (10) дает s * ( ^ ) = 0 (ибо w * ^a <  (1 + b ) ^{— a} ^ 0) и w * ( ~ ) = [1 + bg (0))] ^{— 1} = (1 + b ) ^{— 1} (в отличие от модели (1)–(3), у которой для любых МП s , ( « ) = ^ и w * ( ^ ) = 0).

На рис. 5 приведены графики функций s _* (α) и w * (a), порожденные тремя моделями с b = 0,01 и теми же тремя МФ вида (5), что и на рис. 4 (сплошные, штриховые и пунктирные линии), для семи скоростей сдвига: a = 1; 3;9; 20; 50; 100; 1000 (голубые, черные, зеленые, желтые, синие, красные и фиолетовые кривые). Начальное значение s * (0 + ) = a и предел s * ( ^ ) = 0 не зависят от МП b , но с уменьшением b (при b ^ 0) кривые s * (a) убывают к асимптоте s * = 0 все медленнее, а кривые w _* (α) с разными а все больше сплющиваются к своей общей асимптоте w * = (1 + b ) ^{— 1}, сливающейся с w * = 1 при b ^ 0 (см. голубые кривые), ибо w * (0 + ) = (1 + bg ( a )) ¹ ^ 1.

Итак, зависимости координат положения равновесия s * ( a , b , a ) и w * ( a , b , a ) и кажущейся вязкости (12) от МП b и a монотонны в области a , b , a >  0 .

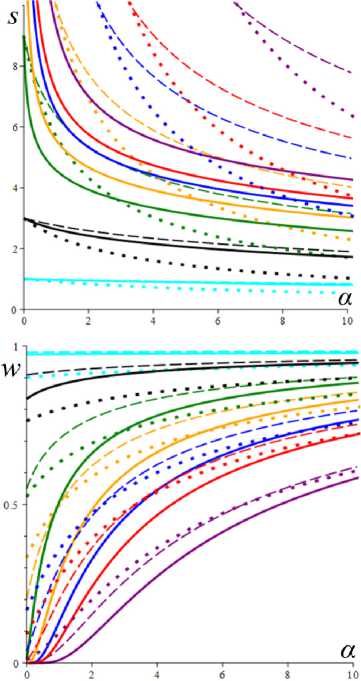
Рис. 5. Графики зависимостей s*(α) и w* (α) для моделей с b = 0,01 и тремя разными МФ (5) (сплошные, штриховые и пунктирные линии соответственно) при семи скоростях сдвига:   a = 1; 3; 9; 20; 50; 100; 1000    (голубые,   черные, зеленые, желтые, синие, красные и фиолетовые кривые)

Fig. 5. Graphs of dependences s _* (α) and w _* (α) for models with b = 0.01 and three different material functions (5) (solid, dashed and dotted lines, respectively) at seven shear rates: a = 1; 3; 9; 20; 50; 100; 1000 (blue, black, green, yellow, blue, red and purple curves)

Зависимость положения равновесия и кажущейся вязкости от скорости сдвига

Исследуем зависимость s _* , µ и w _* от параметра a = v n₀/T c , т.е. их зависимость от скорости сдвига v (и от МП П ₀). Возрастание реологической кривой s * ( a ), убывание кривой вязкости h( v ) и существование конечных пределов при V ч 0 и V ч ^ - важнейшие качественные свойства типичных кривых вязкости, наблюдаемых для разных псевдопластичных жидкостей [3–30]. В статье [56] они доказаны для модели (1)–(3), докажем их и для модели (1), (3), (4).

Производные вязкости (12) и структурированности (10) по а выражаются формулами

/           а-1 '          -1 / ц = По аw* w* = ацw* w*, w' = F 'Ss *) s ' = - bw*2 g 'Ss*) s'*

(производные по а для краткости обозначаем штрихом: s ’ = д у / д а , w ' = д w * / d а , ц' = дц / д а). Поэтому sgn ц = sgn w ' , sgn w ' =— sgn s ' и интервалы монотонности величин р, w * и s * по а совпадают, причем возрастание s * , равносильно убыванию р и w * . Производная (10) по а :

а 2( s' а — s*) = а w*1—1 w', s' а — s* =— а 2а w*1—1 bw*2 g'(s *) s', и с учетом (14)

s ' = s * а '[1 + аЬ а w * ^{a + 1} g '( s * )] ^{— 1} = s * а )l + b а w * s * g '( s * )] ^{— 1}. (15)

В силу g '( s ) >  0 и положительности МП и s * для любых МП верна оценка 0 <  s ' <  s * а ¹ <  1. Поэтому равновесное напряжение s * = у ( а , Ь , а) - возрастающая функция параметра а (и скорости сдвига v) на интервале а >  0, а равновесные структурированность (10) и кажущаяся вязкость (12) убывают по а и по v (как у исходной модели (1)-(3)). Однако у модели (1)-(3) s * ( а ) растет гораздо быстрее и s ' >  s * а ^{— 1} >  1 [56].

Найдем пределы s * ( а ), w * ( а ) и кажущейся вязкости (12) при а ч+ 0 и а ч » , т.е. при v ч 0 и v ч» . Перейдем к пределу при а ч 0 или а ч» в тождестве (11) и докажем, что s * (0 + ) = 0 и s * ( +» ) = +» , причем пределы величин s * / а и р конечны в обоих случаях (они отличаются лишь множителем П ₀) и ц (0 + ) > ц ( +» ) >  0 при любых МП и МФ.

При а ч 0 правая часть тождества (11) стремится к [1 + bg(s*10+))| а (предел s*(0+) существует и конечен в силу возрастания неотрицательной функции s* (а)), и потому существует конечный предел левой части (11), s*/а ч [1 + bg(s*(0+))]—а > 0, следовательно, s* ч 0 и s*/а ч Q , Q = [1 + bg(0)]-а = (1 + b)—а      (16)

(Q(b, а) убывает по обоим аргументам и Q < 1, в отличие от модели (1)-(3), у которой Q = eа/(1+b) > 1, и возрастает по а). По (10) w* ч Q1/а = (1 + b) , а по (15), (16) ц = n0s*/а ч n0Q и s'(0+) = Q при а ч 0. При а ч» правая часть тождества (11) стремится к [1 + bg(s*(+»))]—а (предполагаем, что предел s*(+») конечен), и потому существует конечный предел левой части (11): s*/а ч [1 + bg(s*(+»))]—а . Значит, предположение s*(+») <+» неверно (тогда бы s*/а ч 0) и s*(+») = +» , s*/а ч [1 + bg (+»)]“ = 0 (так как g(+») = +»), ц = n0s*/а ч ц» = 0, и w* ч 0 при а ч » . У модели (1)-(3) тоже w*(а) ч 0 , но остальные пределы при а ч » иные: s*/а ч 1, ц» = п0 > 0 и отношение ц0 / ц» = eа/(1+b) > 1 конечно [56].

Зная s*(0+) = 0 и s'(0+) = (1 + b)—а, из (14) можно найти и пределы остальных производных при а ч +0 : w'(0) = — bw*(0)2 g'(0)s' (0) = — b(1 + b)—2—а g'(0) < 0 , ц'(0) = n0аw*(0)а—1 w'(0) = —ап0b(1 + b)—2а—1 g'(0)< 0 . (17)

При любых МП отношение w ' (0)/ s ** (0) = = — b (1 + b ) ^{— 2} g '(0) такое же, как у ОС (1)-(3), а величина ц ' (0)/ w ' (0 + ) = ар₀ Q (1 + b ) иная. Если g '(0) = 0 (вторая функции (5)), то w ' (0) = 0 и ц ' (0) = 0 .

Таким образом, пределы равновесных кажущейся вязкости (12), напряжения и структурированности при а ч 0 + и а ч » (т.е. при vч 0 и v ч ») и начальный угол наклона s'(0+) кривой течения s*(а), выражаются формулами ц0 = П0Q, ц» = 0, s*(0+) = 0, s*(+») +»,     „

1                               (18)

w * (0) = (1 + b Г¹, w * ( +» ) = 0

s * / а ч 0 при а ч » ; s ' (0 + ) = Q <  1, ^w ' ^{(0 + )} = — b (1 + b ) ^{— 2} g '(0) , ^ц/ ^{0 + )} = ап (1 + b ) ^1—а . (19) 0 s * (0 + )                     w * (0 + )

Очевидно, из (18) при любых положительных МП и любой МФ следует, что ц » <  ц₀ и ц₀ зависит лишь от параметров а, ц₀, b (и не зависит от других МП модели (1)-(3) и от МФ g ( s )). Таким образом, модель описывает общее свойство ц » <  ц₀ типичных кривых вязкости, наблюдаемых для разных псевдопластических жидкостей (часть эффекта тиксотропии).

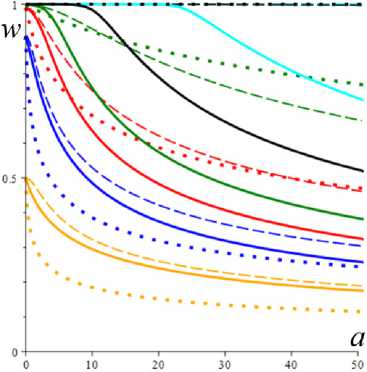
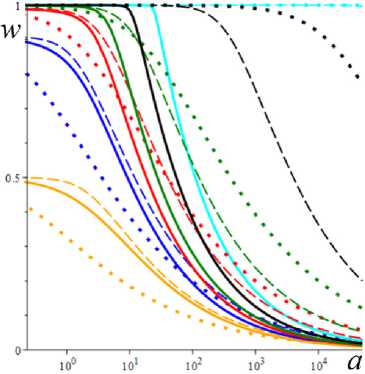
На рис. 6 приведены графики равновесных напряжения и структурированности s*(а) и w*(а) (т.е. зависимостей от скорости сдвига v ), порожденные моделями с фиксированными МП а = 2 , в = 1 и теми же тремя МФ вида (5), что и на рис. 4 и 5 (сплошные, штриховые и пунктирные линии), для шести значений b = 10—12; 10 6; 10—3; 0,01; 0,1; 1 (голубые, черные, зеленые, красные, синие и желтые кривые). Как доказано выше, для любых МП и МФ функции s*(а) неограниченно возрастают, а w*(а) убывают и стремятся к общей асимптоте w* = 0 при а ч » , а с ростом МП b s* и w* убывают (кривые смещаются ниже). На кривых s*(а) с малыми b заметен прямолинейный начальный участок, производная в нуле s' (0+) = Q зависит от b, но при малых b эта зависимость не заметна, ибо по (16) Q ^ 1 при b ^ 0 . С уменьшением b этот участок ньютоновского поведения среды удлиняется, как и начальная «полка» на графиках w* (a) (рис. 6, b). При b < 0,01 она не заметна на рис. 6, b, но переход к шкале lga (рис. 6, d) позволяет увеличить участок малых скоростей и увидеть эту полку (и точку перегиба) на всех графиках w* (a). На рис. 6, c, приведены те же кривые течения s*(a), что и на рис. 6, а, но в шкалах lgs*–lga.

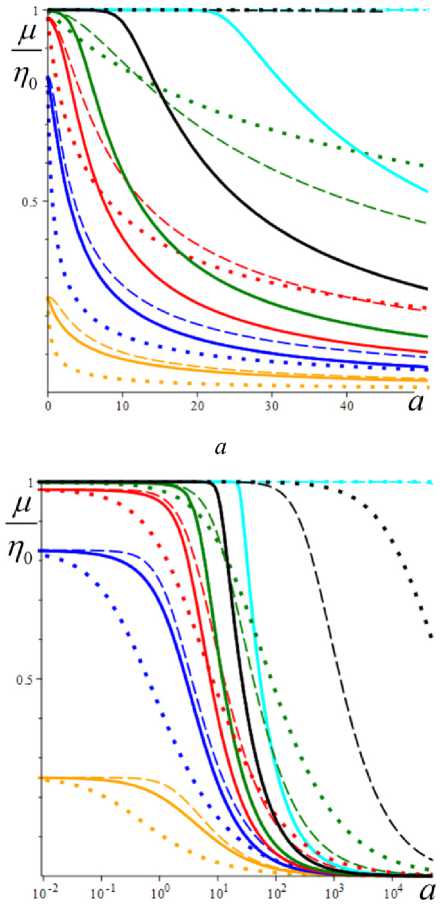
На рис. 7, а , приведены графики зависимости от a обезразмеренной кажущейся вязкости ц( a )/п₀ = = Т * /(vn₀) = s * (a )/ a , порожденные теми же моделями с фиксированными МП а = 2 , в = 1 и тремя МФ вида (5), что и на рис. 4–6 (сплошные, штриховые и пунктирные линии), для шести значений b = 10 ^{- 12};10 ^{- 6}; 10 - 3 ; 0,01; 0,1; 1 (голубые, черные, зеленые, красные, синие и желтые кривые). Зависимость от скорости сдвига ν получается сжатием вдоль горизонтальной оси.

b

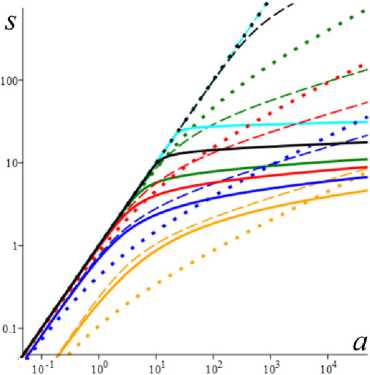
Рис. 6. а , b - зависимости s * ( a ) и w * ( a ) от параметра a =V n₀/T c (скорости сдвига) порожденные моделями с фиксированными

МП а = 2 , в = 1 и теми же тремя МФ вида (5), что и на рис. 4 и 5 (сплошные, штриховые и пунктирные линии), для шести

d

значений b = 10 ¹²;10 ⁶;10 3 ;0,01;0,1;1 (голубые, черные, зеленые, красные, синие и желтые кривые); c - те же кривые течения s _* ( a ) в шкалах lg s _* – lg a ; d – зависимости w _* от lg a

Fig. 6. a , b - dependences of s * ( a ) and w * ( a ) on parameter a = V n₀/T _c (shear rate) generated by models with fixed material parameters а = 2 , в = 1 and the same three material functions of type (5) as in Fig. 4 and 5 (solid, dashed and dotted lines), for six values b = 10 ¹²;10 ⁶;10 3 ;0.01;0.1;1 (blue, black, green, red, blue and yellow curves); c - the same flow ranges s * ( a ) in ranges lg s * - lg a ; d – dependences of w _* on lg a

Как доказано выше, для любых МП и МФ функции ц( a ) убывают и стремятся к общей асимптоте ц = 0 при а ^ ж , а с ростом МП b вязкость убывает (кривые μ( a ) смещаются ниже). На кривых μ( a ) с малыми b заметен горизонтальный начальный участок (участок ньютоновского поведения среды). Переход к шкале lg a (рис. 7, b ) позволяет увидеть эту полку (и точку перегиба) на всех графиках μ( a ) при достаточно малых скоростях сдвига; с уменьшением b этот участок удлиняется, а выход на асимптоту ц = 0 замедляется.

b безразмерной кажущейся вязкости порожденные моделями с

Рис.  7. Графики

ц(a)/n0 = s*(а)/ а , фиксированными МП а = 2 , в = 1 и теми же тремя МФ вида (5), что и на рис. 4–6 (сплошные, штриховые и пунктирные линии), для шести значений b = 10-12;10-6;10-3;0,01;0,1;1 (голубые, черные, зеленые, красные, синие и желтые кривые);

b – зависимости μ /η₀ от lg a

• Fig. 7.    Graphs of dimensionless apparent viscosity ц( a )/n₀ = s * (а )/ a generated by models with fixed material parameters а = 2 and в = 1 and the same three material parameters of type (5) as in Fig. 4-6 (solid, dashed and dotted lines) for six values b = 10 ^{- 12};10 ^{- 6};10 ^{- 3};0.01;0.1;1 (blue, black, green, red, blue and yellow curves); b) dependences of μ /η₀ on lg a

Кривые течения и вязкости, порожденные ОС (1), (3), (4), качественно воспроизводят типичные свойства экспериментальных кривых разных сред (растворов и расплавов полимеров, дисперсных и коллоидных систем, нанокомозитов с эластомерной матрицей, паст) [1–52; 61–65] – см. рис. 1, 2 для суспензий и нанокомпозитов и рис. 8, 9 для расплавов и растворов.

b

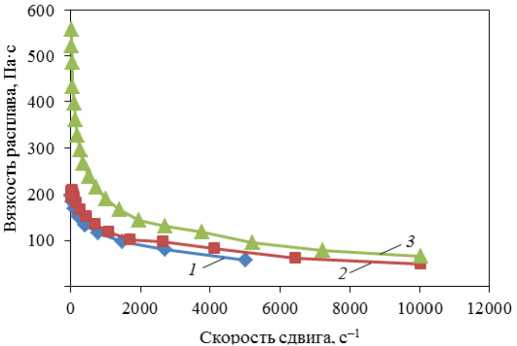
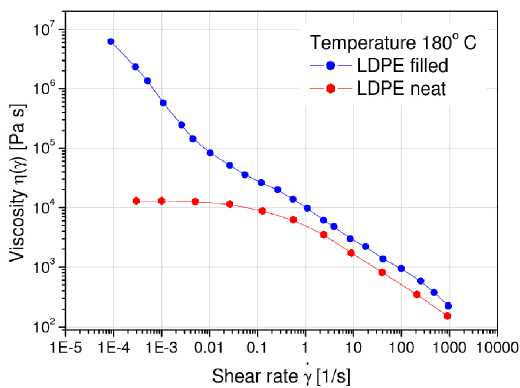
Рис. 8. Кривые вязкости расплавов: а – полиэфирэфиркетона разных марок при температуре 400 °С; b – полиэтилена низкой плотности и дисперсно-наполненного ПНП при температуре 180 °С

• Fig. 8.    Melt viscosity curves: a – polyetheretherketone of different grades at a temperature of 400 °C, b – low-density polyethylene and dispersed-filled LDPE at a temperature of 180 °C

0.5

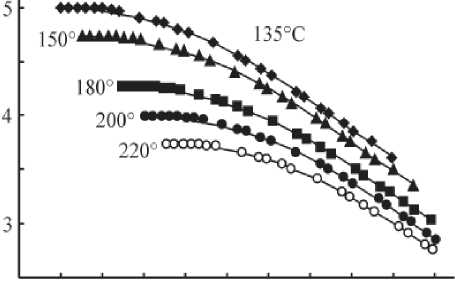
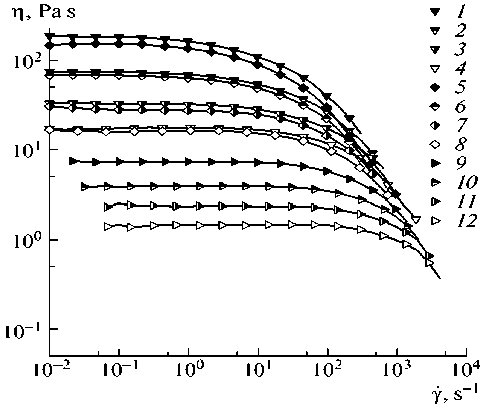
На рис. 8, а , приведены кривые вязкости расплавов полиэфирэфиркетона разных марок при температуре 400 °С [84], на рис. 6, b – расплавов полиэтилена низкой плотности и дисперсно-наполненного ПНП при температуре 180 °С. Наполнение повышает вязкость расплава при малых скоростях сдвига, сужает диапазон линейности (постоянства вязкости), эти эффекты зависят от концентрации наполнителя, размера и формы его частиц, интенсивности взаимодействий между ними. На рис. 9, а , приведены кривые вязкости расплавов расплава полиэтилена низкой плотности при разных температурах [85], на рис. 9, b , – кривые вязкости растворов тройных сополимеров на основе полиакрилонитрила (10 %) при разных температурах (кривые 1 , 5 , 9 – при 20 °С, 2 , 6 , 10 – при 40 °С, 3 , 7 , 11 – при 60 °С, 4, 8, 12 – при 80 °С) [86].

a

b

Рис. 9. Кривые вязкости: а - расплавов расплава полиэтилена низкой плотности при разных температурах, b - растворов тройных сополимеров на основе полиакрилонитрила (10 %) при разных температурах

• Fig. 9.    Viscosity curves: a - low-density polyethylene melts at different temperatures, b - solutions of ternary copolymers based on polyacrylonitrile (10%) at different temperatures

Зависимости w * (a ) модели со степенными зависимостями (4) (рис. 6, b , d) качественно мало отличаются от модели (1)-(3) с теми же МФ g , но w * ( a ) медленнее стремится к асимптоте w * = 0 при а ^ ^ . Существенное отличие кривой течения s * (а ) модели со степенными зависимостями (4) от модели (1)-(3) с экспоненциальными n( w ) и G ( w ) - свойство s * / а ^ 0 при а ^^ (а не s * /а ^ 1), т.е. гораздо более медленный рост, отсутствие асимптоты при а ^ ^ и нулевой предел ц ^ = 0 (а не ц „ = п₀ >  0). Кривые течения s * ( а ) модели (1)-(3) с МФ (5) обладают наклонной асимптотой, параллельной прямой s = а и лежат выше этой асимптоты (в отличие от рис. 6, а ). Это еще один индикатор применимости первого или второго вариантов модели, удобный для проверки по данным испытаний материала.

Теорема о свойствах равновесных напряжения, структурированности и вязкости

Подытожим основные доказанные выше свойства точки равновесия системы уравнений (6), (7).

ТЕОРЕМА. Пусть а , b , a, c , n₀, G ₀ >  0 , в >  0 и функция g ( s ) непрерывна и кусочно дифференцируема при s >  0 , не убывает, g (0) = 1 и g ( +~ ) = +~ . Тогда система дифференциальных уравнений (6), (7) имеет в области {( s , w )| s >  0, w е (0;1)} единственную точку равновесия ( s * , w * ) , она удовлетворяет системе (10) , зависит лишь от трех параметров а , а = v p₀/T _c и b = k ₂/ k 1 (и не зависит от c , в , G₀) и всегда лежит в области 0 <  s * <  а & 0 <  w * <  1 (и даже в более узкой области aF ( а )^а <  s * <  а (1 + b ) ^{- а} &  F ( а ) <  w * <  1/(1 + b )), а функции s * ( а , b ,а) , w * ( а , b ,а) , а , b , а >  0 , и кажущаяся вязкость р ( а , b , а) (см. (12)) обладают следующими свойствами:

• 1)    существуют пределы s * (а , b , а) и w * ( а , b , а) при а ч+ 0 и а ^ ^ (т.е. при v ^ 0 и V ^ ^ ):

s * (0 + ) = 0 , w * (0 + ) = (1 + b ) ^{- 1} и s * ( +^ ) = +“ ; w * ( +^ ) = 0 , s * /а ^ 0 при а ^ ^ ;

• 2)    функции s * (а , b ,а) и w * ( а , b ,а) монотонны по каждому из аргументов в области а , b , а >  0 ;

• 3)    s * и w * убывают по параметру b, д s * / д b = - а а w *¹⁺¹ g ( s * ) / (1 + ab а w *¹⁺¹ g '( s * ));

• 4)    функция s * (а , b ,а) убывает по а на интервале а >  0 , а w * ( а , b , а) возрастает по а ;

• 5)    равновесное напряжение s * (а , b ,а) - возрастающая функция параметра а ( и скорости сдвига v, и МП П ₀) на интервале а >  0 , а равновесная структурированность (10) убывает по а и по v, производные s * и w * по а выражаются формулами (15) и (14);

• 6)    кажущаяся вязкость ц( а , b , а) монотонно убывает по b, а и а и существуют пределы ц( а ) при а ^ + 0 и а ^ ^ : ц₀ = п₀ (1 + b ) ^{- а} <  п₀ и ц ^ = 0 (максимальная и минимальные вязкости);

• 7)    пределы равновесной вязкости (12) , производных напряжения и структурированности при а ^ + 0 и а ^^ (т.е. при v^ 0 и v^^ ) и начальный угол наклона s' * (0 + ) реологической кривой s * (а ) выражаются формулами (18),(19);

• 8)    время релаксации модели (1), (3), (4) T ( w ) = T ₀ w ^{а - в} , T₀ = п₀/ G₀, возрастает с ростом w и меняется в диапазоне (0; T₀ ] ; равновесное время релаксации T * = T₀ w *^{1 - в} , возрастает по w * и имеет тот же тип монотонности, что и w * по всем параметрам; T * убывает с ростом скорости сдвига, при а ^ + 0 T * ^ T ₀(1 + b ) ^{- (а - в)} , а при а ^ ~ T * ^ 0 .

Заключение

Сформулирован новый вариант нелинейного определяющего соотношения для описания сдвигового течения тиксотропных вязкоупругопластичных сред учитывающего взаимное влияние процесса деформирования и эволюции структуры (кинетики ее образования и разрушения), предложенного ранее в [54]. Зависимости вязкости и модуля сдвига от текущей структурированности w ( t ) задаются теперь двумя степенными функциями вместо экспоненциальных η( w ) и G ( w ). В одноосном случае модель (1), (3), (4) управляется неубывающей (кусочно-гладкой) материальной функцией и шестью положительными параметрами, как и модель (1)–(3), но система двух нелинейных дифференциальных уравнений для напряжения и структурированности, к которой она сведена, получается иной. Проведено аналитическое исследование ее математических свойств и характерных особенностей, доказаны существование и единственность точки равновесия ( s _*, w _*) этой системы, в общем виде исследованы зависимости ее координат от всех материальных параметров модели и от скорости сдвига при произвольной материальной функции (они задаются в неявной форме системой двух нелинейных уравнений (10)), доказано, что все эти зависимости монотонны.

Доказано, что новый вариант модели тоже приводит к возрастающей зависимости равновесного напряжения от скорости сдвига и к убывающей кривой ка- жущейся вязкости, отражающим типичные свойства экспериментальных кривых течения псевдопластиче-ских сред, но ряд качественных свойств этих кривых и фазовых кривых отличается от первого варианта модели. Самые существенные из этих отличий: 1) вязкость, модуль сдвига и время релаксации – возрастающие функции w, как и ранее, но при w ^ 0 стремятся к нулю, т.е. в предельном случае модель описывает некую жидкость с низкими структурированностью, вязкостью и модулем сдвига – в отличие от первого варианта модели с ненулевыми пределами; 2) совершенно иной тип зависимости точки равновесия (s*,w*) и величины D(a), определяющей тип точки равновесия, от параметра α (показателя в (4)); 3) качественно иная оценка для равновесного напряжения s*(a): s*(a) < a, вместо s*(a) > a (это простой для проверки индикатор применимости первого или второго вариантов модели); 4) иная асимптотика кривых течения и вязкости s* (a) и р(a) при a ^ ^ : как и в первом варианте модели s* ^ +^ и w* ^ 0, но теперь s*/a ^ 0 и р ^ 0, при a ^^ , вместо s*/a ^ 1 и р^ = п0 > 0. Поэтому новый вариант модели полезен как дополнение инструментария для моделирования течения разнообразных тиксотропных вязкоупругопластичных сред, различающихся поведением кривых течения и вязкости (а также кривых деформирования, релаксации, ползучести и восстановления).