Вариант теории термопластичности для монотонных и циклических процессов неизотермических нагружений

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2020PNRPU MECHANICS BULLETIN

В условиях неизотермического нагружения нестационарные и несимметричные процессы циклического деформирования, состоящие из последовательности монотонных и циклических режимов нагружения, сопровождаются также изменением температуры материала. Математическое моделирование таких неизотермических процессов, особенно в условиях мягкого (контролируемые напряжения) нагружения, представляют собой весьма сложную задачу. Что же касается оценки и прогнозирования ресурса в условиях неизотермических, нестационарных и несимметричных циклических нагружений, то в этих случаях накопление повреждений необходимо определять по всему процессу деформирования, учитывая, что накопление повреждений может быть существенно нелинейно.

Моделирование процессов деформирования и накопления повреждений при неизотермических, циклических нагружениях строится в основном на вариантах теорий пластичности, относящихся к классу теорий пластического течения при комбинированном упрочнении, обзор и анализ которых содержатся в работах [1–42]. Раздельное описание процессов монотонного и циклического нагружения приводится в весьма незначительном числе работ [15, 36, 37]. Для разделения процессов монотонного и циклического нагружения в этих работах вводится поверхность памяти в пространстве девиатора микронапряжений с определением в процессе де- формирования максимального значения интенсивности микронапряжений. В рамках такого подхода происходит лишь изменение размера поверхности памяти, что не позволяет описывать такие тонкие эффекты процессов монотонного и циклического нагружения, как посадка петли упругопластического гистерезиса и разупрочнение материала после монотонного нагружения и др.

В настоящей работе математическое моделирование процессов деформирования и накопления повреждений базируется на варианте теории пластичности [7–14] и обобщено на неизотермическое нагружение.

На основе анализа [14] результатов экспериментальных исследований образцов из нержавеющей стали 12Х18Н10Т при жестком (контролируемые деформации) процессе деформирования, включающем в себя последовательности монотонных и циклических режимов нагружения, в условиях одноосного растяжения-сжатия и различного уровня температур выявлены некоторые особенности и различия процессов изотропного и анизотропного упрочнений при монотонных и циклических нагружениях. Для описания этих особенностей в рамках теории термопластичности, относящейся к классу теорий течения при комбинированном упрочнении, в пространстве тензора пластических деформаций вводится поверхность памяти, разделяющая процессы монотонного и циклического деформирования. Формулируются основные положения и уравнения теории термопластичности. Приводятся материальные функции, замыкающие теорию термопластичности для нержавеющей стали 12Х18Н10Т при различных уровнях температуры. Рассматриваются результаты расчетных и экспериментальных исследований жесткого циклического деформирования в условиях изотермического и неизотермического нагружения вплоть до разрушения нержавеющей стали 12Х18Н10Т. Анализируется кинетика размаха напряжений и среднего напряжения цикла в процессе изотермического и неизотермического циклического нагружения. Получено надежное соответствие расчетных и экспериментальных результатов.

1. Основные положения и уравнения теории термопластичности

p

^£ и *

p

^£ и *

3   sij <7 ij

2 *

° и

— b^tT

E + 3 G

*

3 G

s * ( £ ij —a fT )

— b^tT

^M , x ^M , x 2 j**^^ E * = q + 2 g m ) + 2 ₈im ) 3 - ij -i j m = 1         m = 1      ²    ° u

M

BT = Qt + 2 g m=1

* „( m ) T ( m ) 3 ^-ij^-ij

— Г» *

² °u u

, G = ( ^E A .

² ( 1 + v )

Материал однороден и начально изотропен. Рассматриваются только поликристаллические конструкционные стали и сплавы. В процессе упругопластического деформирования в материале может возникать только пластическая деформационная анизотропия. Рассматриваются малые деформации при температурах, когда нет фазовых превращений, и скоростях деформаций, когда динамическими и реологическими эффектами можно пренебречь. Случаи больших градиентов температур не рассматриваются. Учитываются особенности и различия процессов монотонных и циклических режимов нагружения.

Рассматривается весьма простой вариант теории термопластичности, являющийся частным вариантом теории неупругости [7, 11]. Вариант теории относится к классу одноповерхностных теорий течения при комбинированном упрочнении.

Далее приводится сводка основных уравнений теории термопластичности.

N ^{( 4 )} = 500

° U = C П £ P * >  0   — упругопластичность. (9)

^{52 1} - ?’£ p

(D = a® ^a ——-.             (10)

W a

ep

^£ j ^£ ij ^{+ £} у ,

£ e = E [° j —v ( 3 ° 0 ⁵ i —° j ) ]^+a t ,       (2)

a

£ T ij

= ^a T ^ lj

^— 72 [° ij ^v l ³ ° 0 ^a p ^— ° j ) ]^x E

dE x--- dT

^— E ( ³ ° 0 ⁵ ij

—

\ d v ° ^ij ) dT'

f(°ii )=2(sj — -J)(—j — -j) — C2 = 0.

A£(4)= 0,01(4)

M

- у = 2 - P .

m = 1

Здесь £ ij , £ j , £ P - тензоры скоростей полной, упругой и пластической деформаций; ° j , - ij , - * , - j - тензор напряжений, девиаторы напряжений, активных напряжений и микронапряжений; £ Up * - накопленная пластическая деформация; ® - мера поврежденности; E , v , a _T -модуль Юнга, коэффициент Пуассона, коэффициент температурного расширения; C – радиус (размер) поверхности нагружения ( f ( ° j ) = 0 ) ; - j¹ , - ^{( 2 )} , - j ) ( m = 3,..., M ) - микронапряжения (девиатор смещения центра поверхности нагружения) первого, второго и третьего типов; W_a – энергия разрушения;

( m ) _( m ) ( m )

Q _£ , Q_t , g( , g_a , g_- ( , a - определяющие функции, связь которых с материальными будет приведена ниже.

При деформировании материалов могут иметь место как монотонные, так и циклические режимы нагружения, каждый из которых имеет свои особенности [14]. Для разделения процессов монотонного и циклического деформирования в пространстве тензора пластических деформаций £ ^p вводится поверхность памяти, ограничивающая область циклического деформирования. Поверхность определяется положением ее центра ^ j- и ее радиусом (размером) C _£ . Уравнение поверхности памяти принимается в следующем виде:

- ij” ) = 3 g ⁽ m ) £ p + g -m ) a im ) £ P * + g T ⁽ m )<) T ( m = 1,..., M ) .(6)

1 *

p    ^{d f      3 j} p                     _* I ³ I ²

^£ ij   ,     ^ -,    * ^£ Up* , s ij = ^-ij ^{— -}ij ,   ° u =1 Vil - I , ⁽⁷⁾

^d ° ij    ² ° u                           V ² J

F (4 ) = | ( £ P —5 , )( £ Р —6 , ) — С 2 = °-

Для вычисления положения центра и размера поверхности памяти вводится два тензора пластической деформации £у ^{( 1 )} и £ ^{р ( 2 )} , определяющие границы поверхности. В начале деформирования эти переменные

равны нулю. Определение смещения и размера поверхности памяти происходит в момент смены направления пластического деформирования. В качестве критерия смены направления принимается следующее условие:

g ^W = E a ,

q a

—

E

E

K

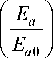
nE

при F ( e p ) < 0,

0 при F ( e j ) > 0,

A С  A С < 0

ij ( t ^{— 0} ) ч ( t )

где ^A p ( t )

- тензор скоростей пластической деформации

T ( 1 ) = ^{1    dE}a 0

E a 0   dT ’

g ⁽M- , g a e ^{2 )} ,

в текущей момент времени t ; A ^p ( t _ ₀ )

- тензор скоростей

пластической деформации в предшествующий ( t — 0 )

T ( 2 ) ₌ ¹ dC?

g a       _g( ² ) dT ’

a

момент времени t . В этот момент координаты центра и размер поверхности памяти вычисляются на основе следующих соотношений:

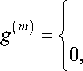
p( m) a( m), если am) > 4m) П aim) s* > 0(m = 3  M)

_Fp ( ²) _ _f p ^{( 1 )} _fp ^{( 1)} _ pp ^A j = ^A j ’ ^A j = ^A j

^ 4 =

_F p ( 1 ) ^A j

+ A

P ^{( 2 )} ij

g a m ) = 0   ( m = 3,..., M ),

CA =

_? f _e^{p ( 1 )}

2 Aj

—

p (W _f p ( 1 ) ij         ^A j

__F p ( 2 ) ) ^A j

1 j _( m )

T ( m ) = ¹ d ^ a ^ga     „( ^m ) dT

^ a

a Um ) =f j a im ) a ( m ( m = 3,..., M ),

Тогда условием циклического деформирования является деформирование в пределах поверхности памяти F ( e pp ) <  0, а условием монотонного деформирования - ^F ( A p ) > °-

При экспериментальном исследовании [14] блочного нагружения, состоящего из чередующихся этапов циклических и монотонных нагружений, выявлены следующие особенности деформирования:

• -    после циклических нагружений монотонные процессы имеют одинаковые модули упрочнения;

• -    после монотонных нагружений имеют место одинаковые процессы посадки петли пластического гистерезиса при циклических нагружениях;

• -    после циклических нагружений происходит увеличение изотропного упрочения при монотонных нагружениях;

• -    после монотонных нагружений происходит уменьшение изотропного упрочнения при циклических нагружениях.

На основании изложенных выше особенностей монотонных и циклических нагружений для определяющих функций имеют место [14] следующие соотношения и уравнения, обобщенные на неизотермическое нагружение:

E a

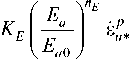
- I E a ⁰ E a I a p E                 U * *

I  Ea 0   J

при F (ep )< 0, при F(ep)> 0,

a (^ ' ? / a * ¹») " " , a *      2 a j=> a

Итак, теорию термопластичности дующие материальные функции:

замыкают сле-

E ( T ) , v ( T ) , a _T ( T ) - упругие параметры;

E_a о ( T ) , ^G am ) ( T ) , P ( m ) ( T ) ( m = 2,..., M ) - параметры анизотропного упрочнения;

K_E ( T ) , n_E ( T ) , M E ( T ) - модули анизотропного упрочнения при циклическом и монотонном нагружении;

K_C ( T ) , n_C ( T ) , M_C ( T ) - модули изотропного упрочнения при циклическом и монотонном нагружении;

C_p ( A Up * , T ) - функция изотропного упрочнения при циклическом нагружении;

W_a ( T ) - энергия разрушения;

n _a ( T ) - параметр нелинейности процесса накопления повреждений ( n _a = 1,5 практически для всех конструкционных сталей и сплавов).

qa = ]

d Cp dA p

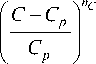
при F ( e p ) < 0,

d CP

—^p + M.

de\ u *

C

при F ( e p ) > 0,

C d C p C p d T ’

2. Базовый эксперимент и метод идентификации материальных функций

Для определения материальных функций достаточно следующего набора экспериментальных данных при различных уровнях температуры:

- упругие параметры E , v , a _T , которые определяются традиционными методами;

• –    участок диаграммы монотонного деформирования после предварительного циклического;

• –    размахи напряжений при жестком циклическом деформировании до разрушения;

• –    посадка петли пластического гистерезиса и восстановление размаха напряжения при жестком циклическом деформировании после монотонного.

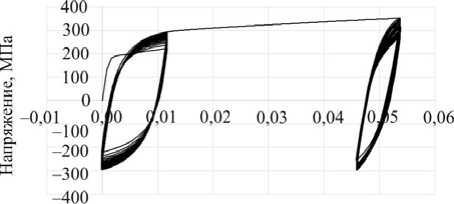
Наиболее простым вариантом получения этих данных является проведение следующего базового эксперимента (рис. 1), состоящего из трех этапов нагружения:

• 1 -й этап – жесткое циклическое нагружение при средней деформации е^ = 0,004...0,005 и размахе Ле^{( 1 )} = = 2 е ^ . Число циклов N ^{( 1 )} = 30...50 до стабилизации.

• 2 -й этап – монотонное растяжение до е^{( 2 )} = 0,04...0,05.

• 3 -й этап – жесткое циклическое нагружение при

( 3 )     „( 2 )

средней деформации     е ^v_m' = e^v ' и размахе

Ле^{( 3 )} = 0,008...0,01 до разрушения.

Деформация

Рис. 1. Базовый эксперимент

Fig. 1. The basic experiment

Метод идентификации материальных функций на основе результатов базового эксперимента приводится в работе [14].

В табл. 1, 2 приведены материальные функции нержавеющей стали 12Х18Н10Т при наборе температур 20,300,400,500,600 ° С, полученные по результатам базовых экспериментов на основе метода идентификации [14].

Таблица 1

Материальные функции стали 12Х18Н10Т

Material functions of 12X18H10T steel

Т , °С	Е , МПа	V	a T , 1/град	Wa , Дж/cм3	E a 0 , МПа	KE , МПа	n E	ME , МПа	KC , МПа
20	198 000	0,28	1.64E-05	1830	1000	7000	3,5	5 000 000	260
300	195 000	0,32	1.74E-05	1400	1000	5000	2	5 000 000	76
400	192 500	0,325	1.78E-05	1300	1000	5800	2,8	5 000 000	218
500	190 000	0,33	1.82E-05	1100	1000	6600	3,5	5 000 000	360
600	170 000	0,33	1.85E-05	1400	500	3000	1,3	150 000	140

Таблица 1. Продолжение

n C	MC , МПа	Р ( 2 )	а р , МПа	Р ( 3 )	а( а 3) , МПа	Р ( 4 )
1.4	600	260	140	10000	15	4000
1.1	600	390	110	20000	10	6670
1.3	550	395	110	20000	9.5	6670
1.5	500	400	110	20000	9	6670
1.7	300	530	110	20000	9	6670

Таблица 1. Продолжение

а р ** , МПа	Р ( 5 )	С 5 , МПа	Р ( 6 )	а( а 6) , МПа	Р ( 7 )	а( а 7) , МПа
36	2000	38	1000	25	670	7
24	2860	26	2000	16	1000	5
22.5	2860	24	2000	15	1000	4.5
21	2860	22	2000	14	1000	4
21	2860	22	2000	14	910	4

Таблица 2

Функция изотропного упрочнения C p ( е Up , , T ) , МПа The isotropic hardening function C_p ( е „^р , , T ) , MPa

T , ° C / е Р *	0	0,0003	0,0006	0,0014	0,0045	0,006	0,01	0,025
20	180	150	135	120	85	75	60	65
300	100	85	75	60	25	20	20	50
400	75	60	50	40	10	10	10	43
500	110	100	92	77	40	42	45	60
600	75	65	57	40	10	7	8	23

Таблица 2. Продолжение

0,1	0,15	0,3	0,45	0,6	1	6	8	25	45	65
90	100	112	115	120	124	132	130	135	140	150
75	85	100	105	110	110	110	110	135	140	145
70	80	90	90	90	90	90	115	135	145	157
90	100	115	120	120	120	120	120	140	140	152
65	80	110	110	110	110	110	115	110	105	120

• 3. Блочное монотонное и циклическое деформирование и разрушение в условиях изотермического и неизотермического нагружения

Для обоснования достоверности расчетов на основе варианта теории термопластичности рассматривается достаточно произвольная программа блочного циклического и монотонного деформирования при температуре 20 °С, состоящая из шести этапов нагружения:

• –    1-й этап включает в себя циклическое нагружение при е^ = 0,004, Ле^{( 1 )} = 0,008 и N ( 1 ) = 500 циклов;

• –    2-й этап включает в себя циклическое нагружение при е^ = 0,006, Ле ( 2 ) = 0,012 и N ^{( 2 )} = 500 ;

• –    3-й этап включает в себя монотонное растяжение до е ( 3 ) = 0,03 ;

• –    4-й этап включает в себя циклическое нагружение при е * ⁴ = 0,025 , Ле^{( 4 )} = 0,01 N ( 4 ) = 500 циклов;

• –    5-й этап включает в себя монотонное растяжение до е^{( 5 )} = 0,05;

• –    6-й этап включает в себя циклическое нагружение при е т = 0,046, Ле^{( 6 )} = 0,008 и N = N f до разру-

  

  Рис. 3. Экспериментальная диаграмма блочного деформирования

  
  

  Fig. 3. The experimental diagram of block deformation

  
  
  

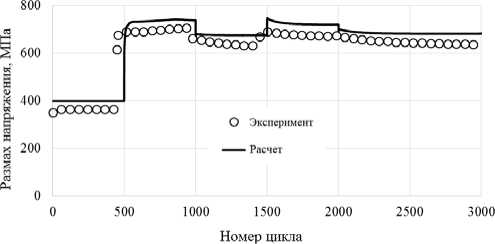
  Рис. 4. Размах напряжения

  
  

шения.

На рис. 2, 3 приведены расчетная и экспериментальная диаграммы деформирования стали 12Х18Н10Т, включающая все шесть этапов нагружения.

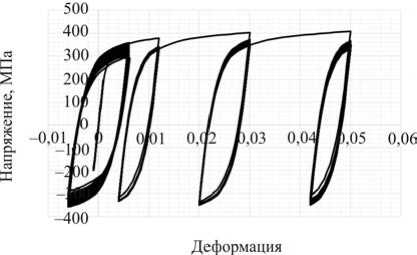
Рис. 2. Расчетная диаграмма блочного деформирования

Fig. 2. The computational diagram of block deformation

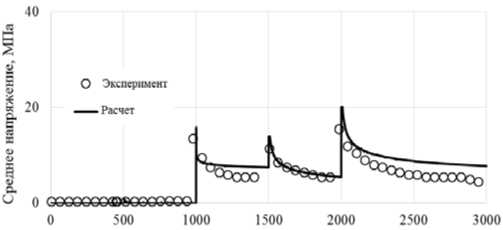
На рис. 4, 5 показаны расчетные (сплошные кривые) и экспериментальные (светлые кружки) результаты изменения размаха и среднего напряжения цикла на первом, втором, четвертом и шестом этапах нагружения.

Экспериментальное число циклов до разрушения составило 7000, а расчетное – 7600.

Fig. 4. The stress range

Номер цикла

Рис. 5. Среднее напряжение

Fig. 5. The average stress

Далее рассматривается неизотермическое нагружение при жестком симметричном циклическом деформировании в условиях растяжения-сжатия с амплитудой деформации, равной 0,004. В процессе циклического деформирования образец нагревался и охлаждался в печи. Зависимость температуры образца от номера цикла нагружения приведена на рис. 6. Расчетное (сплошная линия) и экспериментальное (кружки) изменение размаха напряжения в процессе циклического неизотермического деформирования показано на рис. 6. Экспериментальное число циклов до разрушения составило 6000, а расчетное – 5500.

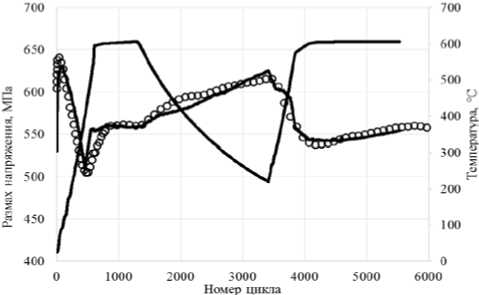
Рис. 6. Температура образца и изменение размаха напряжения в зависимости от номера цикла нагружения

Fig. 6. The sample temperature and stress range depending on the number of the loading cycle

Заключение

На основе анализа результатов экспериментальных исследований нержавеющей стали установлено, что изотропное и анизотропное упрочнения существенно