Вдавливание сферического штампа с шероховатой поверхностью в упругое трансверсально-изотропное полупространство с функционально-градиентным покрытием

Введение. Контактным задачам для функционально-градиентных материалов и покрытий посвящено большое количество современных исследований. Однако, большинство известных в литературе результатов получены лишь для частных случаев изменения упругих свойств в покрытии. Возникающие при этом интегральные уравнения решаются в основном численно и полученные решения эффективны лишь в некотором ограниченном диапазоне значений геометрического параметра задачи (относительная толщина покрытия) [1–3].

При проведении эксперимента по наноиндентированию используют штампы с различной формой наконечника. Наиболее распространены штампы сферической, пирамидальной или конической формы. Однако, в процессе изготовления штампа не удаётся добиться идеальной формы наконечника, кроме того форма штампа может изменяться в процессе эксплуатации [4]. Перед проведением экспериментов форма наконечника индентора обычно отдельно изуча- ется с помощью, например, растрового электронного микроскопа [5, 6]. Однако, математическое моделирование, позволяющее учесть отличие формы штампа от идеальной, изучено очень слабо.

В настоящей работе разработана модель, позволяющая учесть неровности поверхности штампа и непрерывнонеоднородную или кусочно-однородную анизотропную структуру покрытия. Рассмотрена контактная задача о вдавливании недеформируемого штампа в трансверсально-изотропное полупространство с функционально-градиентным покрытием. Основное отличие от аналогичной задачи для изотропных материалов состоит в схеме построения трансформанты ядра интегрального уравнения (функции податливости среды). В работе предложена схема построения функций податливости при действии произвольных осесимметричной нормальной и касательной нагрузок. Считается, что форма штампа неидеальна, неровности поверхности модулируются отрезком ряда Фурье-Бесселя. Построено приближенное аналитическое решение контактной задачи, асимптотически точное для малых и больших значений относительной толщины покрытия и обладающее высокой точностью для покрытий средней толщины.

Построение функций податливости. Рассмотрим упругое неоднородное полупространство Ω с верхней гранью Γ. С полупространством связана цилиндрическая система координат r , φ, z. Ось z нормальна поверхности Г и совпадает с осью анизотропии. Модули упругости полупространства изменяются по законам:

c kj

c k,c ) ( z ) c ⁽ s' ) = const

- H <  z <  0

,(kj) = 11,12,13,33,44, - м < z < - H где c(cc) (z) — непрерывно-дифференцируемые функции, определяющие закон изменения упругих модулей в покрытии (-H < z < 0 ), c(s') (z) — постоянные, определяющие значения упругих модулей подложки. Здесь и далее индексы (c) и (s) соответствуют покрытию и подложке соответственно. Покрытие и подложка жестко сцеплены между собой:

z = - H : w ^{( c} ) = w ^{( s} ) , u ⁽ с ) = u ^{( s} ) , ^ zc ) ° ' ) , 4 c ) =T ^z ) . (1)

Рассмотрим действие произвольной осесимметричной нормальной и касательной нагрузок в круговой области 0≤ r ≤ a покрытия. Вне этой области поверхность не нагружена:

° z|

I z = 0

- P ( r ), r <  a .

0, r >  a ’^Trz*-

I z = 0

т ( r ), r <  a 0, r >  a

.

Определяющие соотношения для трансверсально-изотропного материала имеют вид:

d u     u     d w

d u    u     d w

° r = ^с 11 — ⁺ C 12- ⁺ C 13 — , ° Ф = ^C 12 — ^{+ с}11- ^{+ с} 13— , d r      r       о z          d r     r       о z

d u  u

d w

° z = ^с 1з |— + -I + с 33— , I d r   r 1        d z

( dud т = c     + — I.

rz44

Idzd

Уравнения равновесия ввиду симметричности относительно координаты φ принимают вид:

^d° r + ^dT rz +° r d r    d z

Используя преобразование Ханкеля

м

—

r

°_ ₌ 0,  ^^ r^ . ^d° ^z +brL = 0.

d r    d z    r

м

u ( r , z ) = -J u ( y , z )J 1 ( y r ) y d y , { w ( r , z ), p ( r ), t ( r ) } = J { w ( y , z ), p ( y ), т ( у ) } J 0 ( y r ) y d у

и соотношения (3), уравнения (4) можно преобразовать в систему двух обыкновенных дифференциальных уравнений второго порядка с переменными коэффициентами:

w '( с ₁₃ + c ₄₄ ) y + wc 44 y + u"c ₄₄ + u'c 44 - uc _ny² = 0,

• _ w"с ₃₃ + w'с 3 ₃ - wc ₄₄ y ² - u ' ( с ₁₃ + c ₄₄ ) y - uC ‘ ₃ y = 0.

Граничные условия (1) и (2), используя (5), принимают вид:

z = -H : w(c) = w(s), u(с) = u(s),

₇ _ U . „ ^{( cc} )     „ c^{c )}.„-7^{( c} )      ^{( ss} )     „ '^{s )}.„-7^{( s} )

z = -H : C33 w   - C13 yu   = C33 w   - C13 yu  ,(8)

• - — и . „(c)    (C)        (c)       (s)    (s)

z = -H : c44 (u   +yw  ) = c44 (u + yw  ),(9)

• (c) V(C)    z>(c)    (C)                z,(c)      C)

z = 0:  c33 w - C13 yu   =-P(y), c44 (u   +yw  ) = T(y4

Перепишем систему (6) в матричном виде:

x' = A(C) • x, - H < z < 0,

	f   0	1	0	0       Л
	(c) Y 2 c 11	(c) c 44	(c) V c 44	„ c (c) + € C ^ '	f u )
(с)	(c) c 44	(c) c 44	Y   (c) c 44y	Y      (c) c4A	u'
	0	0	0	1	, x   w
	(c) „ c 13	(c)    (c) c 13 + c 44	(c) Y 2 c 44	(c) c 33	w
	' r(c)	Y     rcc)	(c)	(c)	V w J
	V   c 33	c 33	c 33	c 33        J

Для однородной подложки ( z <- H ) система (11) упрощается до системы обыкновенных дифференциальных уравнений с постоянными коэффициентами:

x' = A(s) ■ x, z <-H,(12)

	f    0	1	0	0       )
	(s) Y 2 c 11_ Y As)	0	0	c(s)+ As) -Y c 13 + c 44 (s)
A (s) -	c 44			c 44
	0	0	0	1
		(s)    (s)	(s)
	0	c 13 + c 44 Y     ((S)	2 c 44 Y /47	0
	V	c 33	c 33	J

Помимо граничных условий (7) –(10) полагаем, что выполнены условия затухания смещений на бесконечности:

u(r,z) ^ 0, w(r,z) ^ 0.(13)

z ^-M

Будем искать решение систем (11) и (12) в виде:

x⁽ с) ( y ,z) = — p( Y ) Y ' a⁽ с) ( Y .z) + т ( Y ) Y ' a 2 с) ( Y ,z), x^(s)( y ,z) = - p( Y ) Y^{- 1} afs V Y ,z) + T ( Y ) Y ' a i^ Y ,z). Тогда, ввиду линейности, получаем системы для определения векторов а ( с ) , a ( ^s ) :

a jc) = A^(с ) ■ a (^c) ,j = 1 , 2 , a f) = A ^(s) ■ a^^j = 1 , 2 .

Общее решение системы (16), соответствующей подложке, имеет вид:

a^ Y ,z) = £ D jk ( y ) j e ^{а k Y} z k = 1

.

Здесь kjk e R, (j = 1,2; k = 1,2,3,4) — известные постоянные, зависящие от упругих модулей подложки, их значения не приводятся ввиду громоздкости; αk — корни биквадратного характеристического уравнения:

а к

^(c11^c 33 ^{- c}13 ^{- 2 c} 13 ^c 44 ) ± У ^(с в ^{- c}11^c 33 ^{)( 4 c} 44 ^{( c} 13 ^{+ c} 44 ^{)+ c} B ^{- c}11^c 33 ) ^{2 c} 33 ^c 44

В общем случае a _k различны. Кратные корни возникают, если выполнено одно из условий: с 2 ₃ = c₁₁ c ₃₃ или

(с13 + 2c44)2 = cH c33, например, в случае изотропного материала. Подробно процесс построения функций податливо- сти для случая кратных корней описан в работе [7], поэтому далее будем полагать, что αk различны. Параметры Djk(γ) подлежат определению из граничных условий. Из (13) следует, что коэффициенты при слагаемых, соответствующих αk с отрицательной вещественной частью, равны нулю. Обозначим корни с неотрицательной вещественной частью через α1 и α2. Тогда (17) принимает вид:

a ^s ( Y ,z) = D j 1 ( y ) k j 1 e “ ^{1 Y} z + D j 2 ( y ) k j 2 e “ ^{2 Y} z .

Граничные условия относительно векторов a ⁽ _j ^с) ,a ⁽ _j ^s) принимают вид:

z = - H:a(^(c) = a^s, j = 1 , 2 ,

^{( c} ) ^{( c} )_/ ^c )   ^{( c})-A^s ) ⁽ s ) _ A ^s )   ⁽ s )

^z = H • с 33 ^aj 4    ^C 13 ^{Y a}j 1 = ^C 33 ^aj 4    ^C 13 ^{Y a}j 1 ,

₇_u._r ⁽ c )   ⁽ c )     ⁽ c )     ⁽ s )   ⁽ s )     ⁽ s )

z = H . c 44 ^{( a}j 2 + ^{Y a}j 3 ) = c 44 ^{( a}j 2 + ^{Y a}j 3 ),

/

z = 0 :

(c)  (c)

с 33 ^aj 4

—

(c)   (c)

^с 13 ^{Y a}j 1

V

(c)   (c)      (c)

^c 44 ^{( a}j 2 ^{+ Y a}j 3 ) J

= Y^ e j^,e 1

П f 0

I e =1 0 J   ² V 1

.

Таким образом, для вычисления неизвестных a(^c) = ^^ ,a(p) .a¹-^) ,a^(c2 T получены две краевые двухточечные задачи для систем обыкновенных дифференциальных уравнений с переменными коэффициентами (15) и граничными условиями (19) -(21). Неизвестные D j _k (у), j , k=1,2, находятся из условия (18). Введем функции эффективных упругих модулей:

V c 44 ( /         ,    )      4^c 11 ^c 33 ^{- c} 13

Al^c 33                  V V ^c 11 ^c 33 + ^c 13 + ^{2 c} 44

,   4444 (1 ------ .    )     7 ^c 11 ^c 33 - ^c 13

и отдельно введём обозначения для их значений, соответствующих подложке и поверхности покрытия: © ( c ) = ©^ (0), © ( s ) = ©^ ( - H - 0). Наконец, введём функции податливости аналогично терминологии А.К. Приварнико-ва [8]:

L kj ⁽ Y ^,z) = © ^М Y ^,z).

Функции Lkj (y, z), k=1,2, j =1,3 не зависят от приложенной нагрузки. В общем случае они могут быть вычислены лишь численно при фиксированном значении γ. При z=0 функции податливости положительны для любого γ, и выполнено lim Lh(y,0) = 1 и lim Lh (y,0) = ©(c) /©(s) ■ Таким образом, значение функции податливости в нуле — есть отношение Y>m j          y^0 j        j I j значений эффективных упругих модулей, соответствующих поверхности покрытия и подложке.

Из (14) получим формулы для смещений точек покрытия в виде линейной комбинации образов преобразования Ханкеля от действующих на поверхности нормальной и касательной нагрузок:

5               L 11 ⁽Y -z ^{A         L} 21 ⁽Y -z ^A

"    ^{( Y ,z)} © p ^t(y)'

w(c)( Y-z) = - L^ p (y)+ L2!^ T(y)                             (22)

Y© ⁽ 3 ^c)         Y© 23 )

Описанная выше схема построения функций податливости может быть использована для сведения смешанных задач теории упругости к решению интегральных уравнений, при этом L^ ( y ,0) будут являться трансформантами ядер этих интегральных уравнений.

Задача о вдавливании штампа. Пусть недеформируемый сферический штамп с неровной поверхностью контактирует с верхней гранью Г полупространства О по области z = 0, r <  a . К штампу приложена вдавливающая сила P , ось которой совпадает с осью z . Силы трения предполагаются отсутствующими [рис. 1]. Под действием силы P штамп переместится в направлении оси z на величину - 5. Считаем, что распределение неровностей (шероховатости) штампа не зависит от угловой координаты и может быть смоделировано отрезком ряда Фурье-Бесселя. Требуется определить распределение контактных нормальных напряжений под штампом: ст _z |_z=0 = - p_a(r), r <  a .

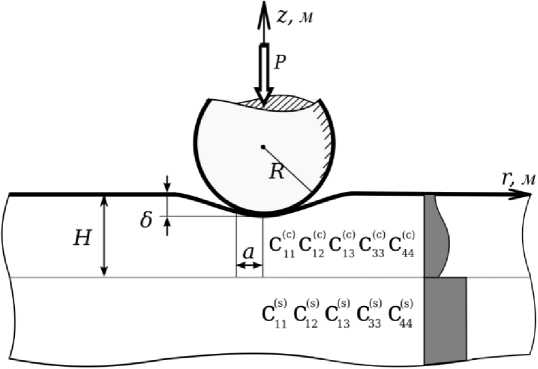
Рис. 1. Постановка контактной задачи о вдавливании

Граничные условия при данной постановке имеют вид:

о'/) — 0,  r > a, z — 0: т (с)

• — 0 , ^                            _

  
  

W ²— —5 + r ²/2 R + Z b_kJ 0 ( ц , r/a), r <  a,

, — 1

где R — радиус сферического штампа (который предполагается существенно больше, чем область контакта, и аппроксимируется параболоидом вращения), ц _к — положительные нули функции Бесселя J ₀ .

Используя (3),  (5), (22) и (23) запишем интегральное уравнение задачи:

¹          ”

J p(x)x J L 13 1 — , 0 I J 0 I — I J, 0      0 V H ) V X )

—x I

0 1 I d—dx — V х)

x< f₈

—

a

V

22 a r

2 R

M

—

Z b k J 0 ( ц k r ‘ ) , r ‘< 1 .

k = 1

)

Здесь X — H/a , r' — r/a , p ( x ) — p_a ( xa ).

Используя двухсторонний асимптотический метод [9, 10] получим приближенное аналитическое решение интегрального уравнения (24):

(s)

4 a v13 p(r ) —   — nR

1 '

+ ZCiAiX— 'J h i —1          r • Jt2 — r '2

dt

—

—

—

2 0 ( |^ M    b j ц j i sin ⁽ц j t )

ⁿ a   j —1 ^l n ^{( X} Ц j)r' 4 t ² _— r ²

dt,  0 <  r ' <  1 .

—

Постоянные C определяются из системы линейных алгебраических уравнений:

Nj(B,X-,AjX-)+ LN(02)R M        ,IBl,цj j—1                      2a    j—1 LN(Xцj) V X

—

(B , X^{— 1} +1 ) X ³ B k ³

.

Здесь к= 1,..., N , i — мнимая единица, L N ( и ) — аппроксимация трансформанты ядра интегрального уравнения:

N— 2 + A2и

LN(u) = П 2      ~ L13(, i—1—2 + в2

F ( B, ц ) —

Bch( ц ) + ц sh( ц )  ch( ц )

B2 —ц2

Соотношения, связывающие радиус сферического штампа, зону контакта, осадку штампа и вдавливающую силу имеют вид:

2а ² n                   n                   M b, cos( ц, )

• 5 — I Z Ci cMAiX2 ) + - + Z (A—2X2 — B—2X2) I + Z  

R ^{V i — 1                 2 i — 1                  7 k} — ¹ L n ( XЦ , )

3   (s)

P — 8 a u_y .

3 R

N

1 + 3 z c i (ch(A i X² ) — A 7 1 X sh(A_iX^-1)) i — 1

+

_{+ 4 0} (c)_a M b j ^{( cos(} ц , ) + ц J^sin( ц J ) . j ^{— 1        l}n^{( Xц} j )

Полученные формулы являются асимптотически точными при Х^0 и Х^да [9]. Алгоритм построения аппроксимаций высокой точности и связь между погрешностью решения для произвольного значения Х и погрешностью аппроксимации трансформанты ядра интегрального уравнения описаны в работе [11].

Выводы. Исследования, представленные в работе, являются естественным продолжением полученных ранее результатов для случая изотропных материалов [12-14]. Для штампов с плоским основанием или конической формы функции податливости среды остаются неизменными, изменяется лишь правая часть интегрального уравнения (35). Решения соответствующих интегральных уравнений построены авторами ранее [7, 13].

Схема построения функций податливости, предложенная в работе, может быть использована при решении ряда контактных задач с учётом одновременного действия на поверхности нормальных и касательных нагрузок и задач с учётом сил трения. Также аналогичная схема может быть применена при решении контактных задач в рамках электроупругости, термоупругости, магнитоупругости и т.д.

Метод решения интегрального уравнения, используемый в работе, позволяет с высокой точностью построить решения контактных задач даже при сложном немонотонном изменении упругих свойств в покрытии [15], а также в случае, когда упругие модули подложки более чем на порядок отличаются от упругих модулей покрытия [12].