"Вечный" двигатель второго рода Андреева

Статья посвящена альтернативному способу получения энергии за счёт охлаждения окружающей среды. В макроскопических устройствах, согласно второму началу термодинамики, это сделать невозможно. Но на микроскопическом, молекулярном уровне это возможно. С точки зрения статистической физики мы опускаемся до таких размеров, когда размер отверстий в мембране сравним с длиной свободного пробега частиц. Это условие накладывает запрет на использования методов статистической физики при расчете взаимодействия мембраны на движение частиц. То есть, второе начало неприменимо к данному двигателю. Принцип работы такого двигателя не противоречит молекулярно-кинетической теории газов. Создание такого двигателя позволит решить проблему загрязнения окружающей среды и глобального потепления.

Часть 1. Конструкция и принцип действия двигателя Андреева

Человечество с каждым годом увеличивает потребление энергии. С каждым годом увеличивается количество машин на дорогах. Сжигается всё больше углеводородов. Загрязняется окружающая среда Повышается температура окружающей среды. В связи с аварией на АЭС «Фукусима» некоторые страны собираются отказаться от АЭС. А это ещё более увеличит сжигание топлива.

Альтернативные источники энергии пока не могут заменить существующие, работающие за счёт сжигания различных видов топлива. Но вокруг нас имеется огромное количество энергии. Она есть везде, в любое время года и дня. Это тепло окружающей среды. Если снизить температуру вод Мирового океана на 1 градус, то этой энергии хватило бы человечеству на несколько столетий при современно уровне потреблении энергии. Но, согласно второму началу термодинамики, это тепло невозможно использовать для получения энергии. Человечество находится в положении потерпевших кораблекрушение - вокруг море воды, а напиться невозможно. Предлагается вариант двигателя, позволяющего получать энергию только за счёт тепла окружающей среды, - см. рис. 1, где 1 - малый цилиндр, 2 - большой цилиндр, 3 - мембрана, 4 - поршень, 5 - опора.

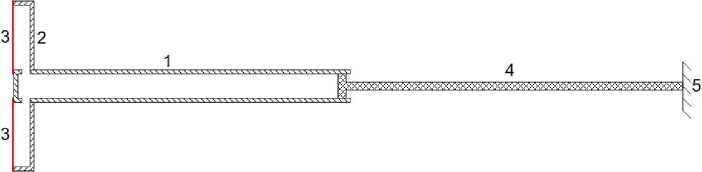
Рис. 1.

Малый и большой цилиндры соединены между собой коаксиально, как единое целое. Главная деталь в этом двигателе – мембрана. Поэтому разберёмся с принципом ее работы. Для лучшего понимания принципа работы мембраны рассмотрим предельно упрощённый расчёт. В мембране множество отверстий размером порядка несколько нанометров. Множество молекул ударяется в мембрану и стенки цилиндров, создавая силу давления. Будем считать тепловые скорости всех молекул одинаковыми - 500 м/с. Также будем считать, что все молекулы двигаются шестью потоками, параллельными координатным осям. Если одну координату расположить по оси малого цилиндра, то один поток молекул будет двигаться влево, оказывая давление на торцевую стенку цилиндра. Другой поток молекул - вправо, оказывая давление на поршень. Остальные 4 потока молекул будут двигаться перпендикулярно оси цилиндра, оказывая давление на его боковые стенки. То есть, в создании давления на торец цилиндра и поршень молекулы 4-х потоков не участвуют. Аналогично в большом цилиндре - один поток оказывает давление на внутреннюю поверхность мембраны, а другой – на внутреннюю поверхность большого цилиндра. Остальные 4 потока оказывают давление на боковые стенки большого цилиндра. Давление оказывают только молекул, которые непосредственно ударяются в торец, поршень, мембрану и находятся в очень тонком слое газа вблизи них. Остальные молекулы внутри цилиндров - это промежуточные элементы. Например, шары Ньютона. Допустим, между крайними шарами находится 1 000 000 промежуточных шаров. Но при ударе в промежуточные шары одного крайнего шара, другой крайний шар отскочит с такой же скоростью, как если бы они столкнулись непосредственно, без промежуточных шаров между ними. Естественно, если считать, что эти удары абсолютно упругие и нет потерь. То есть, все промежуточные шары можно убрать и результат не изменится. Расстояние между торцом и поршнем может быть как 0,1 мм, так и 10 метров. Но количество ударов молекул в торец и поршень в обоих случаях равно. При движении цилиндров с небольшой скоростью вправо, внутренний объём уменьшается. Но количество ударов молекул в торец и поршень также практически будет одинаково. А вот количество промежуточных молекул двух потоков, которые не ударяются непосредственно в торец и поршень, при этом уменьшается. Уменьшается также количество молекул 4-х потоков, которые оказывают давление на боковые стенки малого цилиндра. Эти молекулы вытесняются в большой цилиндр и через мембрану вылетают наружу. Это, примерно как в шарах Ньютона, постепенно удалять промежуточные шары между крайними шарами с 1 000 000 до 0. Но импульсы, передаваемые крайними шарами друг другу, при этом не изменяются – см. рис. 2.

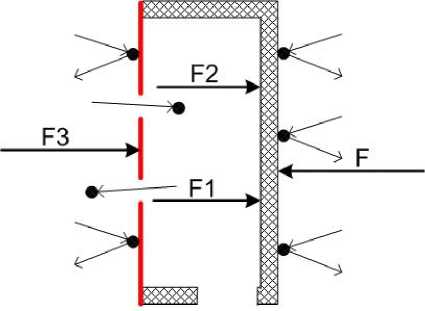
Рис. 2.

Удары множества молекул во внешнюю поверхность большого цилиндра создают силу давления F. Удары множества молекул в наружную поверхность мембраны создают силу давления на мембрану F 3 . Множество молекул, влетающих через мембрану внутрь цилиндра, создают силу давления на внутреннюю поверхность стенки цилиндра F₂. Множество молекул, вылетающих через мембрану из цилиндра, создают реактивную силу F₁, также действующую на внутреннюю поверхность стенки цилиндра. Когда давление газа внутри и снаружи равно, то F = F₁ + F₂ + F₃. Когда в цилиндре избыточное давление, то больше молекул вылетает из цилиндра и появляется дополнительная реактивная сила F₁' от вылета избыточных молекул. Остальные силы не изменяются. F < F₁ + F₂ + F3 + F₁’. На цилиндр действует реактивная сила F₁' от дополнительно вылетающих избыточных молекул. Когда в цилиндре разрежение, то меньше молекул вылетает из цилиндра и реактивная сила F₁ уменьшается. В этом случае на цилиндр действует часть силы F, которая не компенсируется уменьшенной реактивной силой F₁.

Двигатель работает следующим образом – см. рис. 3. В первоначальном положении давления внутри цилиндров и снаружи равны. Одинаковое количество молекул пролетает через мембрану в обе стороны. Система в равновесии. Толкнём цилиндры вправо.

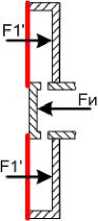
Рис. 3.

При движении цилиндров вправо газ внутри сжимается и больше молекул ударяется в торец цилиндра. Назовём их избыточные молекулы. При ударе каждой избыточной молекулы в торец на цилиндр действует изменение импульса 2mv. Изменения импульсов множества избыточных молекул создают силу избыточного давления на торец цилиндра Fи. В то же время избыточное давление и внутри большого цилиндра, так как оба цилиндра соединяются отверстиями и газ из малого цилиндра поступает в большой. В стенки и мембрану изнутри ударяется больше молекул. Но часть избыточных молекул, которые должны были бы удариться в мембрану, попадают в отверстия мембраны и вылетают наружу. При вылете каждой избыточной молекулы через мембрану на большой цилиндр действует изменение импульса mv. Изменения импульсов, множества вылетевших через мембрану избыточных молекул, создают дополнительную реактивную силу F1'. Эта реактивная сила направлена по ходу движения цилиндров и против силы избыточного давления. Так как 2mv в 2 раза больше mv, то чтобы F1' > Fи, через мембрану должно в единицу времени вылетать более чем в 2 раза больше избыточных молекул, чем ударяется в торец цилиндра. Количество избыточных молекул, ударяющихся в торец при некотором давлении постоянно. Количество избыточных молекул, вылетающих через мембрану при таком же давлении, можно регулировать, изменяя площадь мембраны и количество отверстий на 1 см2 мембраны. Можно подобрать её параметры таким образом, что через мембрану в единицу времени будет вылетать, допустим, в 3 раза больше молекул, чем ударятся в торец цилиндра. То есть, сила F1' будет в 1,5 раза больше силы избыточного давления Fи. На цилиндр будет действовать результирующая сила, равная 0,5 Fи и направленная по ходу движения цилиндров. Под действием этой силы цилиндр будет двигаться вправо с некоторым ускорением, без приложения какой-либо другой внешней силы. Двигаясь вправо за счёт этой силы, цилиндры будут поддерживать внутри избыточное давление. За счёт этого избыточного давления создаётся реактивная сила, которая движет цилиндры вправо. Цилиндры будут двигаться вправо со скоростью, при которой количество молекул, вытесняемых из малого цилиндра в большой и затем вылетающих через мембрану, будет превышать более чем в 2 раза количество избыточных молекул, ударяющихся в торец малого цилиндра. Конечно, на ум сразу приходит рассказ барона Мюнхгаузена о том, как он сам себя вытащил за волосы из болота. Но, в отличие от барона, в данном случае система не замкнутая. При нормальном давлении за 1 секунду в 1 см2 поверхности ударяется примерно 2,25 х 1023 молекул. Площадь поршня - 1 см2. При движении цилиндров вправо, давление внутри обоих цилиндров начинает повышаться и больше молекул начинают вылетать через мембрану, создавая избыточную реактивную силу F1'. В результате при движении цилиндров внутри устанавливается некоторое избыточное давление. Допустим - 0,01 кгс/см2. Сила избыточного давления Fи на торец цилиндра 0,01 кгс.

Эту силу создают удары 2,25 х 1021 избыточных молекул в торец цилиндра за 1 секунду. Движутся цилиндры или неподвижны, но примерно 2,25 х 1021 избыточных молекул ударяются в торец малого цилиндра за 1 секунду. Так можно считать, поскольку скорость цилиндров в сотни раз меньше тепловой скорости молекул. Допустим, за 1 секунду цилиндр сдвинулся вправо на 2 метра. При этом в большой цилиндр из малого было вытеснено 200 см3 газа или примерно 5,4 х 1021 молекул. Но в торец малого цилиндра за это время ударилось только 2,25 х 1021 молекул. Площадь мембраны такова, что все вытесненные из малого цилиндра 5,4 х 1021 молекулы за 1 секунду вылетают через мембрану наружу. Так как давление внутри 0,01 кгс/см2, то в 1 см2 мембраны будет ударяться на 2,25 х 1021 молекул больше. Допустим, площадь отверстий в мембране составляет 50% от всей площади мембраны. То есть, половина из 2,25 х 1021 избыточных молекул, которые должны были бы удариться в 1 см2 мембраны, будет попадать в отверстия в мембране и вылетать наружу. Через 1 см2 такой мембраны за 1 секунду будет вылетать 1,125 х 1021 избыточных молекул. Чтобы вылетело 5,4 х 1021 молекул, необходимая площадь мембраны - 4,8 см2. Эти молекулы, вылетающие через мембрану площадью 4,8 см2 за 1 секунду, создадут реактивную силу F1' - 0,012 кгс. Сила избыточного давления Fи - 0,01 кгс. Результирующая сила, действующая на цилиндры и двигающая их вправо - 0,002 кгс. Если площадь мембраны увеличить в 2 раза до 9,6 см2, то 5,4 х 1021 молекул смогут вылететь за 1 секунду при избыточном давлении 0,005 кгс/см2. Сила избыточного давления 0,005 кгс. Реактивная сила останется без изменений, так как количество вылетевших избыточных молекул не изменится. Соответственно, результирующая сила увеличится до 0,007 кгс. Если цилиндры за 1 секунду пройдут 4 метра, то реактивная сила 0,024 кгс. Сила избыточного давления на торец 0,01 кгс. Результирующая сила 0,014 кгс. Это при площади мембраны 9,6 см2. Изменяя площадь мембраны и количество отверстий в ней, можно подобрать оптимальный режим работы такого двигателя. Под действием этой силы цилиндры будут перемещаться вправо до упора. Эту силу создают молекулы газа за счёт своей кинетической энергии. Когда цилиндры движутся вправо, то молекулы вылетают влево. Их скорость при этом уменьшается на скорость движения цилиндров. Допустим, цилиндры двигаются со скоростью 4 м/с. Тогда скорость вылетающих молекул 500 м/с - 4 м/с = 496 м/с. То есть, кинетическая энергия молекул газа уменьшается.

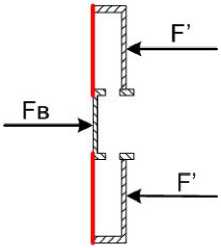
Рис. 4.

Когда цилиндры достигнет крайней правой точки и остановятся, то их можно подтолкнуть в обратную сторону – см. рис. 4. При движении влево внутри цилиндров создаётся разрежение. Меньше молекул вылетают через мембрану из большого цилиндра наружу и реактивная сила F1 уменьшается на F1’. Равновесие сил нарушается. F > F3 + F2 + F1 – F1’. На наружную поверхность большого цилиндра действует часть силы давления F', которая не компенсируется уменьшенной реактивной силой F1. Эта сила F’ направлена по ходу движения цилиндров влево. Так как внутри цилиндров пониженное давление, то на наружную поверхность торца малого цилиндра действует сила внешнего давления Fв, направленная против силы F'. Реактивная сила от вылетающих молекул уменьшается настолько, что F' > Fв. Под действием результирующей силы цилиндры двигаются влево, поддерживая разрежение внутри цилиндров. Цилиндры после первоначального толчка также самопроизвольно дойдут до левой крайней точки. Как и в предыдущем процессе, часть результирующей силы можно использовать для получения энергии. Совершив движение вправо-влево, цилиндры вернулись в первоначальное положение. Цикл завершился. При этом есть возможность получить энергию только за счёт охлаждения окружающей среды. Для увеличения мощности такого двигателя его необходимо поместить в закрытый объём, в котором создано повышенное давление хорошо очищенного газа. Это также снимет проблему засорения отверстий мембраны мельчайшими частицами пыли.

Главное условие работы такого двигателя – отношение числа вылетающих через мембрану избыточных молекул в единицу времени к числу избыточных молекул, ударяющихся в торец малого цилиндра за это же время, должно быть больше более чем в 2 раза. Это условие выполняется, если суммарная площадь отверстий в мембране более чем в 2 раза превосходит площадь поршня. Будучи запушенным в работу, такой двигатель может работать бесконечно долго только за счёт тепла окружающей среды, охлаждая её.

Чтобы не возникало вопросов, почему цилиндры получают импульс mv, когда молекулы влетают и вылетают через мембрану, попробую сразу очень упрощённо объяснить, чтобы такие вопросы снять.

Рис. 5.

Допустим, имеется очень маленькая сфера в вакууме, в невесомости см. рис. 5. В сферу ударяется молекула и отскакивает (а). Под воздействием импульса 2mv сфера движется со скоростью V. В такую же сферу, только с отверстием в стенке, ударяется другая молекула (б). Под действием импульса 2mv сфера также движется со скоростью V. Отскочившая молекула ударяется в противоположную стенку (в). Под действием импульса 2mv сфера останавливается, а отскочившая молекула снова летит к противоположной стенке. При ударе в стенку молекула передаёт сфере импульс 2mv и сфера снова со скоростью V летит дальше (г). Таким образом, сфера половину времени движется со скоростью V, а другую половину неподвижна. Дальнейшие удары молекулы внутри сферы уже не влияют на среднюю скорость сферы. Средняя скорость сферы V/2. Такую скорость сфера приобретёт под действием импульса 2mv/2 или mv.

Рис. 6.

Такая же сфера с прилипшей к стенке сферы молекулой – см. рис. 6. Молекула отлипает и с тепловой скоростью отскакивает от стенки (д). Сфера получает импульс mv и со скоростью V1 движется в другую сторону. Молекула сталкивается с противоположной стенкой сферы (е). Столкновение можно разделить на удар и отскок.

При ударе молекула передаёт сфере импульс mv и останавливает сферу. При отскоке передаёт импульс mv и сфера со скоростью V1 движется в противоположную сторону. При столкновении с противоположной стенкой аналогичный процесс (ж). Сфера колеблется на месте со скоростью V1. Допустим, в стенке сферы появилось отверстие. Молекула попадет в него и вылетает наружу (з). Так как в этом случае молекула не взаимодействует со сферой, то сфера продолжает двигаться со скоростью V1, которую она получила под действием импульса mv. V/2 равна V1.

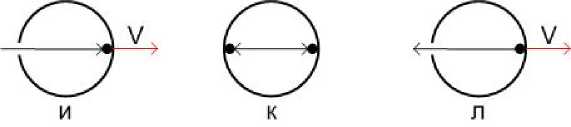
Рис. 7.

В сферу влетает молекула – см. рис. 7. Сфера получает импульс mv и движется со средней скоростью V/2 (и). Затем молекула многократно и долго сталкивается с противоположными стенками сферы (к). Сфера в это время половину времени двигается со скоростью V, а другую половину - неподвижна. В это время средняя скорость сферы V/2, как от импульса mv. Молекула ударяется в стенку и придаёт сфере скорость V (л). Отскочившая молекула попадает в отверстие и вылетает наружу. Сфера двигается со скоростью V, как под действием импульса 2mv. То есть, можно считать, что к импульсу влетевшей молекулы mv, добавился импульс от вылетевшей молекулы mv. Аналогично, если через мембрану цилиндра влетает или вылетает молекула, то цилиндр получает от каждой влетевшей или вылетевшей молекулы импульс mv.

Возьмём мембрану толщиной несколько нанометров и с множеством отверстий размером несколько нанометров. Мембрана является торцевой стенкой цилиндра. Множество молекул движутся к мембране внутри цилиндра. Для примера возьмём две молекулы. Одна молекула сталкивается с мембраной и отскакивает. Цилиндр не получает импульс mv. Другая попадает в отверстие и вылетает наружу. Цилиндр получает импульс mv. Мембрана служит как бы границей, при пересечении которой каждой молекулой цилиндр получает импульс mv. Независимо от того, влетела молекула или вылетела.

Но это в вакууме. В атмосфере во внешние поверхности цилиндра и мембраны ударяются внешние молекулы и оказывают

Доклады независимых авторов 2014 выпуск 26 дополнительную силу давление на эти поверхности. Для простоты представим, что в мембрану и цилиндр в единицу времени ударилось по 9 молекул – см. рис. 8.

Внешняя поверхность цилиндра получила импульс 9 х 2mv = 18mv. Внешняя поверхность мембраны получила 8 х 2mv = 16mv. Но влетевшая и вылетевшая через мембрану молекулы передают на внутреннюю поверхность цилиндра по импульсу mv. 18mv = 16mv + mv + mv. Или F = F 3 + F₂ + F₁. Система в равновесии. Если в сосуде избыточное давление, то из цилиндра дополнительно вылетает избыточная молекула. Тогда 18mv < 16mv + mv + mv + mv'. Или F < F 3 + F₂ + F₁ + F₁'. То есть результирующая сила F₁' будет направлена вправо. Если давление в цилиндре низкое, то из цилиндра молекула не вылетит. Тогда 18mv > 16mv + mv. F > F₃ + F₂ на F₁. Результирующая сила F₁ направлена влево.

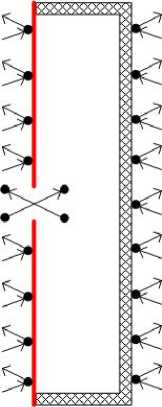
Рис. 8.

Допустим, я изобрёл инерцоид, состоящий из множества валов. Сбоку каждого вала прикреплён грузик. Поэтому при вращении вала он колеблется около центра масс из-за дисбаланса. Все эти колебания валов инерцоида– это внутренние силы, которые не могут привести инерцоид в движение. Валы вращаются с большой скоростью. Но вдруг ось у одного вала ломается и он отлетает в сторону со скоростью 500 м/с. Инерцоид получает импульс mv и движется в противоположную сторону. Другой вал ломается и снова инерцоид получает импульс mv. Допустим, рядом стоит такой же инерцоид. Вылетевший вал из этого инерцоида со скоростью 500 м/с попадает в первый инерцоид и застревает в нём. Первый инерцоид также получает импульс mv. Множество молекул внутри большого цилиндра можно представить в виде множества валов инерцоида. Пока молекулы летают внутри цилиндра и ударяются в стенки и мембрану, их импульсы не могут привести в движение цилиндр, подобно валам в инерцоиде. Но как только молекула вылетает наружу подобно сломавшемуся валу или влетает, то цилиндр получает импульс mv. Допустим, 2 инерцоида соединены сжатой пружиной, которую фиксирует нить. Один инерцоид во много раз массивнее другого. Перерезаем нить и инерцоиды под действием пружины расходятся в противоположные стороны. То, что внутри инерцоидов вращаются множество валов, на движение инерцоиов под действием пружины не влияют. Не будем учитывать гироскопический эффект. Это всё внутренние силы, которые не могут привести в движение инерцоид и не могут оказать влияние на движение инерцоида под действием внешней силы. Лёгкий инерцоид имеет скорость 1 м/с. Тяжёлый инерцоид получил импульс mv, где m - масса лёгкого инерцоида, а v - 1 м/с.

Эти же 2 инерцоида соединены между собой. На лёгком инерцоиде начинают ломаться валы и они со скоростью 500 м/с отлетают в сторону. Причём только в одном направлении. Все валы сломались и отлетели. Тяжёлый инерцоид получает суммарный импульс mV, где m - масса инерцоида, а V - 500 м/с. Будем считать, что масса инерцоида равна массе валов. В обоих случаях от тяжелого инерцоида отделилась одинаковая масса. Но импульс во втором случае в 500 раз больше.

Когда инерцоид отталкивается от другого инерцоида под действием пружины – это аналогично тому, что множество молекул вылетают через большое отверстие. Допустим, множество молекул находятся в безмассовой оболочке (красная) – см. рис. 9.

Рис. 9.

Эту оболочку с множеством молекул можно представить как инерцоид. Удары множества молекул внутри оболочки не могут сдвинуть её с места. Когда давление внутри цилиндра повышается,

Доклады независимых авторов 2014 выпуск 26 то оболочка движется по цилиндру и вылетает наружу со скоростью, допустим, 1 м/с. При движении оболочки удары молекул внутри её также не влияют на движение оболочки. Цилиндр получает импульс mv, где m - это масса молекул внутри оболочки, а v = 1 м/с. Хотя внутри оболочки молекулы движутся со скоростью 500 м/с. Когда же молекулы поодиночке вылетают через отверстия мембраны - это аналог инерцоида, у которого сломавшиеся валы со скоростью 500 м/с отлетают в одну сторону. То есть, суммарный импульс от такого же количества молекул, вылетающих через мембрану, будет в 500 раз больше.

Возьмём для примера осмос. Сосуд разделён на две части мембраной с большими отверстиями. В разных частях сосуда раствор с различной концентрацией. Через большие отверстия будут проходить молекулы и растворителя, и растворимого вещества. Осмотического давление создаваться не будет. Если отверстия уменьшить так, что будут проходить только молекулы растворителя, то больше молекул растворителя будут проходить из одной части сосуда в другой. Объём раствора в одной части увеличивается. Также увеличится и давление в этой части сосуда. То есть, размер отверстий имеет.

Установим на этот двигатель мембрану толщиной 0,001 мм и с отверстиями диаметром 0,001 мм. Затем поместим его в закрытый объём, в котором создадим глубокий вакуум. Вакуум будет везде. В том числе и в самих отверстиях мембраны. Затем запустим внутрь газ и давление внутри станет, допустим, 1 мм рт. ст. При таком давлении длина свободного пробега молекул примерно 0,1 мм. То есть, длина свободного пробега молекул примерно в 100 раз больше диаметра отверстий в мембране. С обоих сторон мембрану вакуума уже нет. Но в самих отверстиях мембраны глубокий вакуум остаётся.

В [1] читаем:

1. Если средняя длина свободного пробега А того же порядка, что и характерный линейный размер сосуда d, в котором заключен газ, или больше, то состояние газа называют вакуумом. Воздух в комнате, например, при атмосферном давлении в состоянии вакуума не находится, так как в этом случае Л ~ 10^-5 см. Однако в сосуде, линейные размеры которого меньше 10^-5 см (поры дерева и многих других пористых тел), тот же воздух уже находится в условиях вакуума.

Различают три вида вакуума: 1) низкий, когда Л меньше характерного размера сосуда d, но приближается к нему; 2) средний, когда А сравнима с d^-, 3) высокий (или глубокий), когда А значительно больше d. Газ в состоянии высокого вакуума называется ультраразрежен-ным.

Отверстия в мембране можно представить в виде микроскопических пор, открытых с двух сторон. То есть, внутренний объём цилиндров сообщается с внешним через тонкую прослойку ультраразреженного газа. Увеличим давление до атмосферного. Длина свободного пробега молекул уменьшится до 10-5 см. То есть, внутри отверстий ультраразреженного газа уже не будет. А будет множество хаотично двигающихся молекул, как внутри и снаружи цилиндра. Чтобы внутри отверстий снова появился ультраразреженный газ, надо уменьшить размер отверстий в мембране. Допустим, толщина мембраны и диаметр отверстия 1-2 нм. Это в 50-100 раз меньше длины свободного пробега молекул. То есть, в таких отверстиях при атмосферном давлении снова будет ультраразреженный газ.

Часть 2. Новый термодинамический циклАндреева

В 1824 году вышла в свет книга С. Карно "Размышления о движущей силе огня и машинах, способных развивать эту силу". В ней автор собирался рассуждать об "обычных" тепловых машинах, состоящих из "...парового котла, парового цилиндра, поршня и холодильника...". Интересно еще отметить, что у Карно приведенные рассуждения не сопровождались ни расчетами, ни графиками. Его книга первоначально резонанса не получила. Лишь через десять лет, в 1834 г., другой француз, Эмиль Клапейрон, придал термодинамике Карно канонический вид. Он ввел все необходимые обозначения, проделал описанные словами вычисления и построил диаграммы. Через три года статью Клапейрона перевели на английский язык и издали в Англии в сборнике Scientific Memoirs ("Ученые записки"). А еще через девять лет на нее обратил внимание немецкий физик и издатель И.Х. Поггендорф, перепечатал в своем журнале Annalen der Physik und Chemie ("Анналы физики и химии"), и только тогда теория Карно действительно увидела свет. Но это не так важно. Важно, что в результате на свет появился термодинамический цикл Карно. Все зациклились на этом цикле, не желая замечать того, что возможен и другой цикл. В цикле Карно рабочее тело сначала получает тепло от нагревателя. Затем часть полученного тепла рабочее тело тратит на производство работы, а оставшееся тепло передаёт холодильнику. Если двигатель работает по такому циклу, то такой двигатель не сможет всё тепло использовать на производство работы. Но возможен и другой цикл. Главное отличие от цикла Карно - это отсутствие холодильника, а нагревателем служит окружающая среда. Первоначально температура рабочего тела и температура окружающей среды равны. Затем рабочее тело совершает работу за счёт своей внутренней энергии. При этом рабочее тело охлаждается, так как часть внутренней энергии тратится на совершение работы. То есть, температура рабочего тела становится ниже температуры окружающей среды. Вполне естественно, что более холодное рабочее тело получает тепло от более тёплой окружающей среды, которая служит в данном случае нагревателем, и восстанавливает свою внутреннюю энергию до первоначального уровня. Нагревание рабочего тела происходит, в отличие от цикла Карно, не до совершения работы, а после. Получив тепло, система вернулась в первоначальное состояние. Цикл закончился. Двигатель, работающий по такому циклу, способен превратить в работу всё полученное тепло, так как более холодное рабочее тело в принципе не может отдать тепло более тёплой окружающей среде, согласно второму началу термодинамики. При работе двигателя часть энергии будет переходить в тепло вследствие сил трения и т.д. Но при последующей работе двигателя это тепло также будет использовано. То есть, кпд такого двигателя = 100%. Остаётся только придумать такой процесс, при котором рабочее тело сможет сначала совершить работу только за счёт своей внутренней энергии. И вуаля, вечный двигатель второго рода готов.

Описанный выше "вечный "двигатель как раз и работает по такому циклу. Допустим, мембрана заменена стенкой с отверстием. Цилиндр совершает от крайней левой точки к крайней правой за 1 секунду. При движении цилиндра внутри создаётся некоторое давление. Повторим цикл, увеличив отверстие. В этом случае давление внутри будет меньше. Ещё увеличим отверстие - давление станет ещё меньше. Когда площадь отверстия станет равна площади поршня или больше, то при движении цилиндра давление внутри будет равно внешнему. Каждому отверстию можно подобрать эквивалентную мембрану. То есть, такую мембрану, через которую вылетает столько же молекул, как через соответствующее отверстие. Соответственно, каждое отверстие можно заменить эквивалентной мембраной. При увеличении площади мембраны давление внутри при движении цилиндра будет уменьшаться, как оно уменьшается при увеличении отверстия, см. график.

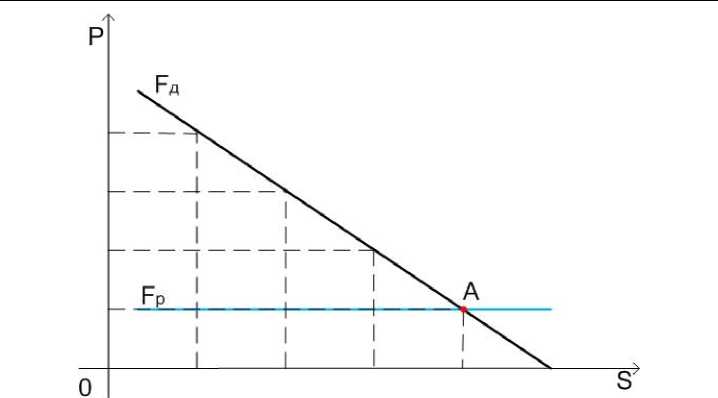
Как видим, при увеличении площади мембраны давление внутри цилиндра при его движении уменьшается. Соответственно, сила давления Fд, действующая на торец малого цилиндра, уменьшается. И при достаточно большой площади мембраны стремиться к 0. Так как во всех случаях через мембрану вылетает одно и тоже количество молекул, то реактивная сила Fр, противодействующая силе Fд, постоянна. До точки А Fp < Fд. В точке А Fp = Fд. После точки А Fp > Fд. Результирующая сила, действующая на цилиндр F = Fp - Fд. При достаточно большой площади мембраны F = Fp. Эта реактивная сила Fp двигает цилиндр, поддерживая повышенное давление внутри цилиндра. А повышенное давление в свою очередь создаёт реактивную силу.

Термодинамический цикл в координатах P,V будет выглядеть следующим образом.

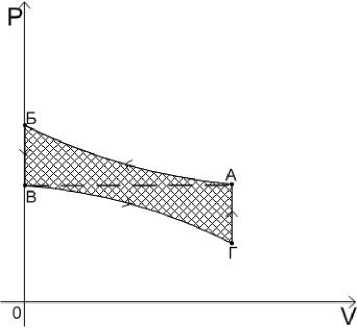
Первоначальное состояние - точка А. Давление внутри равно наружному. Цилиндр сдвинули вправо. Давление внутри повысилось. Появившаяся вследствие этого реактивная сила с ускорением двигает цилиндр вправо. Внутренний объём газа уменьшается, а давление увеличивается, пока цилиндр не достигнет крайней правой точки. Кривая АБ. Когда цилиндр достигнет крайней точки, остатки газа выйдут через мембрану и давление снизится до наружного. Прямая БВ. За счёт запасённой энергии, например в маховике, цилиндр сдвигается влево. Давление внутри понижается, а объём увеличивается. Сила давления внешнего газа действует на внешнюю сторону большого цилиндра, двигая цилиндр с ускорением влево до левой крайней точки. Кривая ВГ. Когда цилиндр достигает крайней левой точки и останавливается, внешний газ через мембрану проникает внутрь и давление внутри сравнивается с наружным. Прямая ГА. Цилиндр вернулся в первоначальное положение. При этом была совершена работа только за счёт охлаждения газа, то есть, окружающей среды.

Возможен и короткий цикл. Когда цилиндр возвращается влево под действием запасённой в маховике энергии, то открывается клапан и внешний газ свободно поступает в цилиндр. Холостой ход, пунктирная линия ВА. А потом цикл повторяется до бесконечности.

Так как реактивная сила возникает при движении цилиндра, то нагрузка не должна превышать некоторой величины, при которой цилиндр будет снижать свою скорость движения. При этом скорость движения уменьшается, количество вылетающих молекул уменьшается, реактивная сила уменьшается и двигатель останавливается. Для увеличения мощности двигателя необходимо повышать давление газа. Например, поместить двигатель внутри оболочки, внутри которой создаётся повышенное давление очищенного от мельчайших частиц газа. Это также решит проблему засорения отверстий мельчайшими частицами.

Может быть, кто-нибудь поправит и приведёт мои рассуждения к более научному виду. Как Эмиль Клапейрон придал термодинамике Карно канонический вид.