Vector Image Retrieval Methods Based on Fuzzy Patterns

Nowadays, the number of images created and stored in vector formats is growing dramatically. The most frequently occurring content of these images is technical drawings and clip arts. Retrieval of such graphical data enables new opportunities for patent search, plagiarism analysis, etc. Besides, there is also another important task, which can be solved with the use of vector images, namely, medical image retrieval. Despite that originally medical images are raster, their processing can require vectorization in many cases, in particular, it can be useful for the detection of a specific shape, retrieval of similar images, feature extraction, etc.

However, vector image retrieval is a complicated task because the same shape can be presented by using different combinations of basic graphical primitives (lines, rectangles, polylines, etc.). Visually, such vectorized shapes can look identically but their internal view can differ considerably because each graphical primitive has its own representation format. The problem of vector image retrieval becomes even more complex if we search not for identical shapes but for similar ones which can be of different size and their vertices coordinates can differ significantly. All these specificities of graphical data representation complicate vector image retrieval.

The research problem is to enable an object retrieval when its shape cannot be defined strictly. In this paper we attempt to solve this problem by employing a fuzzy approach to vector image representation. The main objective of this research is to elaborate a method for the retrieval of vector images described by imprecise data.

The rest of this paper is organized as follows. Section 2 presents the literature review. In Section 3, we propose two approaches to vector image retrieval. The basic method explains the general idea of imprecise graphical data representation based on fuzzy templates of shapes which enables vector image retrieval. The advanced method improves the retrieval accuracy and can be used for the analysis of complex shapes such as objects on medical images. Section 4 presents the practical results and their discussion. Finally, some conclusions are given in Section 5.

• II.    Related Work

Since the task of vector image retrieval is topical, many researchers work in this area. In particular, Fujita and Hayashi [1] proposed a similarity retrieval system for vector images such as trademarks. The proposed system retrieves vector images from a database using a sketch given by the user as a query. The sketch is converted into a vector image format as a pre-processing step for the similarity retrieval.

Jiang et al. [2] presented a prototype system based on SVG technology and the method of similarity measurement. They proposed to measure the similarity between a requested image and a candidate image taking into consideration shape similarity, spatial similarity, color similarity, transformation similarity, and position similarity.

Rahmani and Ansari presented their study [3] of the conventional approaches and techniques used in image retrieval systems.

Hayashi et al. [4] presented a novel method for content-based 2D vector image retrieval. The method includes two main stages. At the beginning, Weighted Feature Points (WFPs) are extracted from vector images. Next, similarity between query and candidate images by matching WFPs is evaluated by using Proportional Transfer Distance (PTD).

Pu and Ramani [5] proposed to analyze a vector image as a whole. In particular, they presented two methods to describe drawings: the first one uses the 2.5D spherical harmonics and the other uses a 2D shape histogram.

Chen and Wang [6] presented a new fuzzy logic approach called UFM (Unified Feature Matching) which enables region-based image retrieval. This approach allows associating an image with a family of fuzzy features corresponding to regions.

Chen and Weng [7] considered a measure of the similarity between two tree structures. They proposed an algorithm for a tree similarity measure based on the weighting subtree and the fuzzy inference system.

Wang and Xie [8] presented the retrieval system which uses the fuzzy language variables to describe the similarity degree of image features as well as it employs the fuzzy inference to instruct the weights assignment among various image features. The authors also proposed an improvement on the Average Area Histogram to represent color features.

Martins et al. [9] studied the benefits of combining information extracted from vector and raster images to retrieve clip arts. The authors proposed to extract color and texture features from raster images while geometry and topology features were extracted from vector images.

Bhute and Meshram [10] presented the content-based image retrieval systems which employ the color, texture and shape information of images.

Banerjee and Kundu [11] presented a robust technique for content-based image retrieval based on using fuzzy edge map of an image.

Krishnapuram et al. [12] described an image retrieval system called FIRST which uses fuzzy attributed relational graphs to represent images.

Uchida et al. [13] proposed the application of the Fisher vector representation to binary features to improve the accuracy of binary feature-based image retrieval.

Fonseca et al. [14] presented a generic approach to content-based retrieval of structured graphics and drawings. The authors proposed to index drawings using a topology graph which describes adjacency and containment relations for parts and subparts in an image.

Li et al. [15] proposed an approach to describe and to extract fuzzy color semantics. The authors applied the feedforward neural network to model the vagueness of human color perception and to extract the fuzzy semantic feature vector.

The analysis of these and other papers allows us to conclude that a fuzzy approach is mostly employed for raster image retrieval. In the next sections, we present our vision on how a fuzzy approach can be applied to vector image retrieval.

• III.    image Representation and Retrieval

• A.    Vector image format

The analysis of these and other papers allows us to conclude that a fuzzy approach is mostly employed for raster image retrieval. In the next sections, we present our vision on how a fuzzy approach can be applied to vector image retrieval.

One of the most popular vector image formats is SVG (Scalable Vector Graphics) [16]. SVG allows describing two-dimensional graphics by using graphical primitives such as lines, circles, polygons, etc. It supports interactivity and animation as well as raster effects applied on the client side when the SVG is rendered. In fact, SVG is a language for describing two-dimensional graphics in XML [17].

The example of SVG code fragment which draws a blue triangle defined by its vertices P ₁ (100,100), P ₂ (300,400), P ₃ (400,200) is given in Fig. 1. This simple SVG code illustrates the main problem of vector image retrieval mentioned in above: to find the image which contains a specific object (e.g. a triangle of a certain size and shape) we need to know crisp coordinates of this object. However, in most cases, we do not have this information and, therefore, we mostly look for objects which are similar to some pattern, but generally not equal to it.

width="l5cm" height= "15cm">

• Fig. 1. SVG code example.

  Note that in further explanations we refer to such similar objects as resembling objects as well as we use the term “resemblance” instead of “similarity” in order to avoid misinterpreting this term used in geometry (similar triangles, similar solids, etc.). On the other hand, resemblance of two objects can be modelled by a resemblance relation introduced in [18, 19].

  In particular, in [19], the resemblance relation is defined as follows: a fuzzy relation E on a pseudo-metric space ( x ,d ) is called a resemblance relation (w.r.t. d) if for all x y z and u in X :

  (R.1) E ( x , x )=1,

  (R.2) d ( x , y ) <  d ( z , u ) implies e ( x , y ) >  e ( z , u ).

  Thus, transition from crisp values of vertex coordinates to fuzzy values can enable effective vector image retrieval.

  • B.    Basic Method

  The idea of the proposed method is based on a geometric interpretation of a fuzziness degree: a “fuzzy” vertex is a circle with the center in this vertex defined by its crisp coordinates and a crisp radius of the circle which limits the neighborhood of the “fuzzy” vertex. Both a pattern image and a candidate image are analyzed in object-by-object manner. Every object is a single shape (e.g. polygon, circle, line, etc.) located at a separate layer of the vector image. Objects in the candidate image are defined by their crisp coordinates as in the example in Fig. 1. Objects in the pattern image are defined by fuzzy coordinates of their vertices. Since a SVG file [16] operates with crisp values only, we propose to add a new attribute “fuzziness” intended to define a fuzziness degree of vertex coordinates (Fig. 2).

  <5vg width"!5 cm " height "15cm ">

  fuzziness="0, 20, 10"/>

  Fig. 2. SVG code with ‘fuzziness’ attribute.

  A value of the attribute “fuzziness” can be defined in millimeter, inch, pixel, etc. As it is mentioned above, this value corresponds to a radius of the circle around the vertex which limits the neighborhood of this “fuzzy” vertex. This idea is described by Fig. 3 where a fuzzy pattern (dotted triangle), vertices fuzziness (grey circles), and a crisp result of image retrieval (solid triangle) are shown. Other conventional signs in Fig. 3 are explained below. The number of possible retrieval results is limited by the value of the neighborhood circle radius.

  

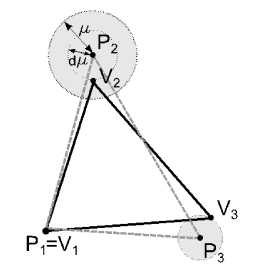
  Fig. 3. A fuzzy pattern and a crisp result of image retrieval.

  The proposed basic method can be used in the following cases:

  • •    A raster image is previously vectorized;

  • •    A graphical object (shape) is created in a vector format.

  In any mentioned case, we suppose that there are two sets of vertices coordinates and two adjacency matrices as input data. The vertices adjacency matrices enable reconstruction of shapes: triangles, rectangles, polygons.

  Any object of retrieval (an element of a pattern) is defined by its fuzzy coordinates. Any object in a candidate image is defined by its crisp coordinates.

  The pattern can be specified by a vertices adjacency matrix A and a set P of fuzzy coordinates defined as follows:

  ^P = { ( Р_г , M i) |i ^ [1, n ] } ,                      ⁽¹⁾

  where p. = ( X. , y. ) is a vertex defined by its crisp coordinates x . and yM ^ is the degree of fuzziness of the vertex p ; as we mentioned it above in the geometric sense fuzziness degree is equivalent to a radius of a circle with the center in the point p ; n is the number of vertices.

  A candidate image can be specified by a vertices adjacency matrix M and a set C of crisp coordinates defined as follows:

  C = { v. \i e [1, n ] } ,                        ⁽²⁾

  where v. = ( x. , y. ) is a vertex defined by its crisp coordinates;

  n is the number of vertices.

  Vertices adjacency matrices A and m are composed in the same way. In particular, matrix A is composed by the following rule:

  n (

  ^R = П 1 ¹ - i = 1 V

  ___________ d M i ___________^ max ( ц 1 , M 2 ,..-, M_n ) + K J

  { 1 if p. and p are connected

  0 if p and p aren't connected

  where i , j ^ [1, n ].

  As the first step of the method, we analyze the vertices adjacency matrix A . As a result of this analysis, we obtain data about the shape of the template object, in particular, the vertices number.

  At the next step, we begin to analyze candidate images (CIs) from image database for the presence of objects resembling to the pattern object. For this purpose, we take a random vertex in the set C as the initial one and search all other vertices, which belong to the same shape, in the adjacency matrix M .

  After reconstructing this shape by the “crisp” matrix M , we need to find the corresponding “fuzzy” vertex in the set P and then the corresponding shape in the “fuzzy” matrix A . Note, values in both adjacency matrices are crisp as it is defined in (3); we use words “crisp” and “fuzzy” (in quotes) to facilitate the understanding to what kind of an object – either a pattern (“fuzzy”) or a candidate image (“crisp”) – this matrix belongs.

  The detection of the corresponding “fuzzy” vertex is fulfilled taking into consideration the fuzziness degree of the vertex. Thus, let v (defined by its crisp coordinates ( _x , y ) be a “crisp” vertex which needs a correspondent “fuzzy” vertex to be found in the set P . Then p (defined by its fuzzy coordinates (x.,y.) and fuzziness degree ц, ) is a required “fuzzy” vertex if the following inequalities hold true:

  where d ц, is a true fuzziness degree for the vertex p with respect to the “crisp” vertex in the pattern object (physical meaning of both _{d ц} and ц. is shown in Fig. 3); n is the number of vertices in the pattern object;

  K ф 0 is a small positive number (e.g. K = 0.01 ) which is necessary to avoid zero fuzziness measure for vertices where the degree of fuzziness ц has maximum value among all other vertices.

  For example, the degree of resemblance of two triangles ( PPP and VV V ) in Fig. 3 can be estimated as R =0.25 if we define values of fuzziness degree as ц =0 , ц =20 , ц =10 (see attribute “fuzziness” in Fig. 2) and d ц =10 . If two shapes are equal, then the degree of their resemblance R =1.

  Alternatively, the degree of resemblance can be estimated according to [18] as:

  R ( object1, object 2 ) = max ( 0, min ( 1, a - d ( object1, object2 ))) ,

  where a >  1.

  Let us consider two vertices v and p defined by their coordinates ( x , y ) and ( x , y ) respectively as object1 and object2 . Then d ( object1, object2 ) can be defined as follows:

  

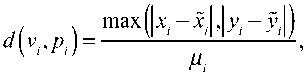
  X. - Ц. < X. < X . + /z. й-/^^Я⁺^, к-^+ь.-й)²-^²

  where ц is a fuzziness degree.

  Let a = 1 + — (щ > 0). Then if two triangles ppp Mi and VV V in Fig. 3 are defined by coordinates P (14,12) , P(32,86), P(80,10), V (14,12), V (32,76), V (86,18) and M = 0 , Ц = 20 , ц = 10, then the degree of resemblance of PPP and VV V can be estimated in the following way:

  When the first “fuzzy” vertex is found, we search for the next “fuzzy” vertices which belong to the same shape.

  R ( V ₁, P ₁)=1,

  If the whole shape of the “fuzzy” object corresponds to the pattern object, we calculate the degree of resemblance of these two objects. This degree can be obtained as a result of multiplication of the fuzziness measure for each vertex:

  (,i

  R ( V , P. ) = max 0,min 1,1 +---

  22       I      l max ( 32 - 32 , 76 - 86 ) 1 ]

  --------------U--------- I I = 0.55, 20

  

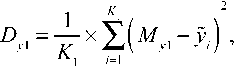
  where M , M are mean values for coordinatesof

  (          (        1

  R ( V, , P - ) = max 0,min 1,1 +---

  ³³        l      l     10

  K 1

  vertices:

  max ( |86 - 80|J18 - 10 |) 11

  --------------^U-------- I I = 0.30.

  10                    I I

  1           1

  M = — хУх. xl v          1

  Then r = 1 x 0.55 x 0.30 = 0.165 . Thus, this estimation is stricter than the degree of resemblance defined by (5).

  The basic method can be used for the comparison of polygons and other primitives in vector images.

  • C.    Advanced Method

  Now let us generalize the proposed geometric interpretation of fuzziness from a circle to an ellipse. This approach gives more flexibility in search of complex shapes.

  An array of fuzzy coordinates     and an array of crisp coordinates x, y are used as initial data for resembling image retrieval in this case. Vertices with fuzzy coordinates     define a pattern image. Vertices with coordinates x, y define a candidate image which is considered as resembling the pattern image if coordinates x, y get into the elliptic fuzziness area. The fuzziness area for a vertex with coordinates      geometrically is an ellipse with radiuses ц x and ц y . These radiuses can be either set manually or calculated. In the latter case, fuzziness values ц x and цy can be defined in two steps. As the first step, we set them as:

  цx = p_x ^x Dx 1 , ц y 1 = Py ^x Dy 1 ,       ⁽⁹⁾

  where цХ1, цУ are the “first-step” elliptic fuzziness area radiuses for coordinates     ;      are “first-step” fuzzy coordinates,             , i=1,...,K; D , D are variance values for coordinates        of K vertices; K is a quantity of vertices for the first step of the retrieval procedure.

  Variance values D , D can be calculated as follows:

  1 Kv

  D - — X^M -x\ ,

  Then the resembling images retrieval accuracy can be defined by coefficients p , p :

  ( M .1

  p = int       ^{x 1}   ,

  ^Х      l D x 1 J

  ( M J ^p y = ^int l^-I

  where int is an operation of rounding by truncation of a number fractional part.

  If we decrease these coefficients, the accuracy increases. It means that for the second step of the retrieval procedure the values of fuzziness should be decreased according to (16) and (17) as well as the quantity of vertices to be analyzed should be increased.

  цx₂ = ( p_x - X ) x D_{x 2},            (16)

  ц y 2 = ( P y ^{- X} )^x D y 2 ,             ⁽¹⁷⁾

  where цx2, ц y2 are the “second-step” elliptic fuzziness area radiuses for coordinates xi, yi; D , D are variance values for coordinates xi, yi of K vertices used in the second step of the retrieval procedure; X = 1,...,min (px, py ).

  The resemblance degree of the candidate image and the pattern image for two steps of the retrieval procedure is defined as a product of the resemblance degrees for all vertices:

  к      к

  Л = ]^[7? = ]~[тах(0;1 +

  /=1           1=1

  

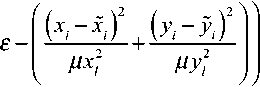
  where R is a resemblance degree of i-vertex, i=1,..., K; K is a quantity of vertices; ε is an arbitrary small positive value (for example, ε=0.000 1 ); x y are crisp i, i coordinates, x, y∈ [0,1] ; х.,у are fuzzy coordinates, хрУ,е[0,1]; µx,µy are fuzziness values, l=1,2.

  If vertices are resembling, thenε≤ R < 1 + ε; if vertices are coincident, then R =1 + ε ; otherwise       .

  i i

  The advantage of this two-step retrieval procedure is evident when an object to be find has a complex shape and a large number of vertices: the first step enables excluding both dissimilar images ( R =0 ) and images with negligible resemblance ( R → 0 ) by analyzing a limited number of vertices; the second step enables finding resembling images by analyzing a full set of vertices.

  To store a pattern image, which is defined by its vertices with an elliptic fuzziness area, we propose to use the extended attribute “fuzziness” with two radiuses defined for every vertex in a modified SVG format (Fig. 4).

  width = "15 cm " height= "15cm ">

  polygonpoints="100,100 300,400 400,200";

  fuzziness="(0,5), (20,15), (10,15)"/>

  Fig. 4. SVG code fragment with “elliptic” fuzziness.

  • IV.    Results and Discussion

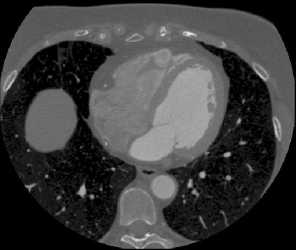
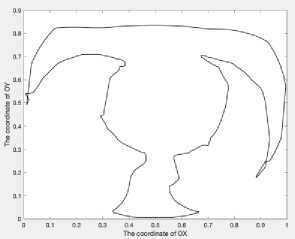
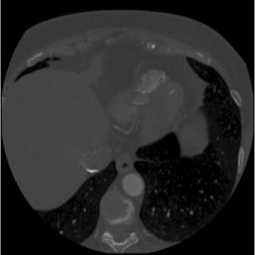
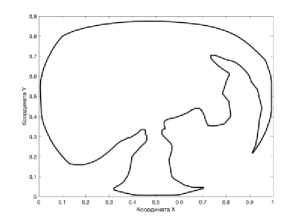
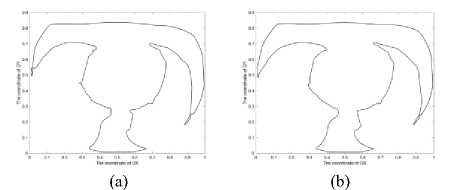
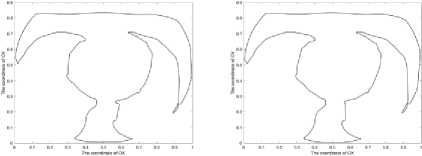
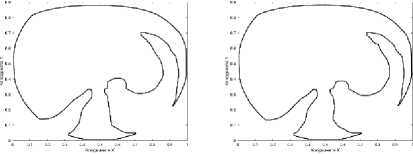
  The objective of the experimental part of this research is to prove that the proposed methods ensure retrieval of resembling objects in a set of images. To achieve this goal, the proposed methods have been realized in the MatLab environment and tested on real images. In particular, the proposed retrieval procedure based on an elliptic fuzziness area (the advanced method) has been tested on medical images, namely, heart computer tomography images. The test data set included 100 candidate images. The retrieval request was defined by using two pattern images (Fig. 5 and Fig. 6).

  

  (a)

  

  (b)

  

  (a)

  

  (b)

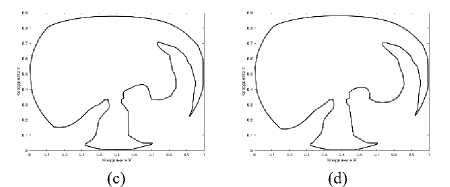
  Since original heart computer tomography images are raster images, they have been vectorized by using the method presented in [20]. This method enables description of an object complex shape by any requested number of vertices. It allows us to describe objects on both a pattern image and a candidate image by the same number of vertices. Naturally, the accuracy of the object vectorization depends on the number of vertices. The first vertex in a shape is the closest to the origin of coordinates.

  

  (c)                                 (d)

  

  (e)                                     (f)

  Fig. 7. The Test Set 1 of vectorized heart computer tomography images: (a) img1_02, (b) img1_03, (c) img1_04, (d) img1_05, (e) img1_06, (f) img1_07.

  The number of vertices for the first step was equal to 949, for the second step it was equal to 1369. For the first step the fuzziness values were µ x =0.4944 , µ y =0.4607 ; for the second step the fuzziness values were µ x =0.4362 , µy =0.3721 . The result of the image retrieval is shown on Fig. 7. The resemblance degree of these candidate images and the pattern image img1_01 obtained at the second step is given in Table 1.

  Table 1. Resemblance degree for img1_01

  Image name	Resemblances Degree
  img1_01	1,1467
  img1_02	1,0232e-05
  img1_03	1,2367e-11
  img1_04	3,6728e-12
  img1_05	2,2502e-18
  img1_06	4,6421e-16
  img1_07	9,1436e-60
  img2_01	0
  img2_02	0
  img2_03	0
  img2_04	0
  img2_05	0
  img2_06	0
  img2_07	0

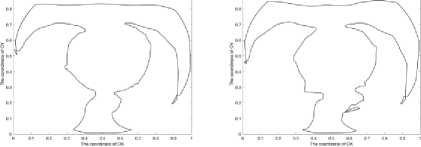
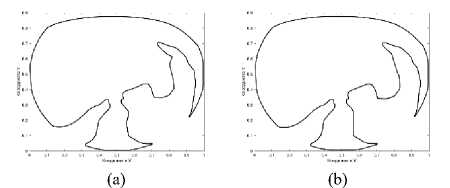
  The number of vertices for the first step was equal to 949, for the second step it was equal to 1369. For the first step the fuzziness values were, for the second step the fuzziness values were. The result of the image retrieval is shown on Fig. 8. The resemblance degree of these candidate images and the pattern image img2_01 obtained at the second step is given in Table 2.

  

  (e)                                     (f)

  Fig. 8. The Test Set 2 of vectorized heart computer tomography images: (a) img2_02, (b) img2_03, (c) img2_04, (d) img2_05, (e) img2_06, (f) img2_07.

  Table 2. Resemblance degree for img2_01

  Image name	Resemblances Degree
  img1_01	0
  img1_02	0
  img1_03	0
  img1_04	0
  img1_05	0
  img1_06	0
  img1_07	0
  img2_01	1.1467
  img2_02	0.0122
  img2_03	0.0066
  img2_04	8.3672e-04
  img2_05	1.1979e-06
  img2_06	9.0422e-07
  img2_07	3.3365e-09

  The comparative analysis of the resemblance degree values (Table 1 and Table 2) and the object shapes (Fig. 5, Fig. 6, Fig. 7, and Fig. 8) allows concluding that the resemblance degree adequately characterizes the visual resemblance of a pattern image and a candidate image. All images which are characterized by zero resemblance degree contain artifacts such as loops and distortions. At the same time, the candidate images with non-zero resemblance degree are visually similar to the corresponding pattern image. What is important that the more similar the pattern image and the candidate image are, the higher the computed value of their resemblance degree is. In particular, Table 1 shows that the pattern image img1_01 (Fig. 5) has the highest resemblance degree with itself and it has zero resemblance degree with the images from the Test Set 2 which have another shape. The rest of the resemblance degree values are non-zero values and the lowest value (9,1436e-60) corresponds to the image img1_07 shown at Fig.7 (f) which includes vectorization artifacts (loops) and, thus, it can be considered as the least resembling image. Similar results are shown in Table 2: the highest resemblance degree is obtained from comparison of the pattern image img2_01 (Fig. 6) with itself (1.1467). The resemblance degree of the pattern image img2_01 and the images from the Test Set 1, which have another shape, is equal to zero. The rest of images have non-zero resemblance degree.

  The accuracy of the proposed methods can be improved by increasing the number of vertices in the shapes of both a pattern image and a candidate image.

  The obtained experimental results allow concluding that the proposed approach based on fuzzy logic can be used for retrieval of vectorized images, including medical images. The advantage of this approach is that most medical images have large size due to their high resolution. Thus, their vectorization can be useful in cases when the images are stored to be a subject of further retrieval. In this case, the use of modified SVG format can help to decrease required data storage volumes.

  • V.    Conclusions

  The use of fuzzy values for the description of a template (a pattern image) allows to make the search more flexible and therefore to achieve better results of vector graphics retrieval.

  Both proposed methods can be especially useful in cases when the shape of an object to be retrieved is described roughly. Human brain makes the search in such uncertain conditions easy, but algorithmic methods can give unacceptable results. Methods based on artificial intelligence approaches enable improving retrieval results, but they are quite complicated in their software realization [21]. Unlike methods based on machine learning which are time- and resource-consuming, the proposed methods based on fuzzy logic do not require training and high computing resources. At the same time, they allow to achieve comparative results in a simpler way. Therefore, the proposed retrieval approach based on fuzzy patterns can be used for search of resembling shapes in vector images. Initial data can be either raster or vector images and objects to be retrieved can have any complex shape. The use of the proposed methods in medical information systems enables efficient study of clinical cases. These methods can be also used for image classification. Application of the proposed methods enables development of new algorithms for data analysis of resembling image groups.