Вейвлет-анализ в обработке сигналов аналитических приборов

Вейвлет-анализ является одним из наиболее мощных и гибких средств исследования и цифровой обработки сигналов: помимо задач их фильтрации и сжатия, анализ в базисе вейвлет-функций позволяет решать задачи идентификации, моделирования, аппроксимации стационарных и нестационарных процессов, исследовать вопросы наличия разрывов в производных и т.д. Вейвлет-преобразование привносит в обработку сигналов дополнительную степень свободы. Например, гармонический анализ Фурье способен показать поведение сигнала в частотной области, остав- ляя открытым вопрос о локализации во времени различных компонент сигнала. Таким образом, вейвлет-функции базиса позволяют сконцентрировать внимание на тех или иных локальных особенностях анализируемых сигналов, которые не могут быть выявлены с помощью традиционного преобразования Фурье.

Непрерывное вейвлет-преобразование (ВП) сигнала f ( t ) имеет следующий вид [1]:

- 1 О

W_f ( a , b ) = a ² J f ( t ) tI — dit,  ⁽¹⁾

-о      V a J где функция ^[ t - b | называется вейвлетом; a, b -

V a J параметры соответственно масштаба и сдвига. Множи-i тель a 2 обеспечивает единичную норму для любой

-L,. t - b.

базисной функции ^ (tt) = a 2 Т(____) • a’                   a

Обратное вейвлет-преобразование записывается в виде:

x 1 ° °                / х dadb

f ⁽ t )  _r J J ^Wf ^{( a} , ^{b ) T} _ab ⁽ t )

^ 0 -о             ^a

Здесь С – нормирующий коэффициент:

° i^ И

C ^ = I       d ^ < г , (2)

И где ^(И) - Фурье-образ вейвлет-функции ^(t) . Из равенства (2) следует условие допустимости использования функции Ф(t) в качестве вейвлет-функции: среднее (нулевой момент) ^(t) должен быть нулевым

M = J ^ ( t) dt = 0 •             (3)

-о

Другое требование - быстрое убывание ^ ( t ) с ростом частоты. Для практических приложений часто бывает необходимым обеспечение нулевых значений первых m моментов вейвлета:

со

Mm = JtmТ(t)dt = 0, m = 0,1,2,... •(4)

-о

Разложим ВП (1) в ряд Тейлора при b = 0 :

-1 (О m1

Wf [a,0]= a 21 £ f(m)(0) f ЦT( t-)dt + O(n +1) , V m=0        -Оm!   aJ где f(m)(0) - производная порядка m ; O(n + 1) -члены ряда Тейлора порядка выше n . Используя определение моментов (4), можно записать:

- ¹ (

W_f [ a ,0 ] - a ² l f (0) M ₀ a + f —(°) M ₁ a ² + I                                   1!

+ f 2(0> M₂a 3 + ... + f ⁽ n ⁾ (2) MX + 11.   (5)

2!        ²                 n !        ⁿ J

В соответствии с (3) M _o = 0 , тогда первый член в разложении (5) является нулевым. Следовательно, ВП постоянного сигнала даст в результате нуль. Таким образом, число нулевых моментов вейвлета определяет порядок полинома, который будет проигнорирован вейвлет-преобра-зованием в анализируемом сигнале. Например, выходной сигнал аналитического прибора имеет составляющую дрейфа базовой линии, которая обычно представляется как полиномиальный сигнал вида d ( t ) = d ₀ + d_xt + d₂t ² , где d ₀, d_x , d₂ – некоторые коэффициенты. При этом коэффициенты d [, d ₂ определяют собственно дрейф, который может вызываться нестабильностью режимов аналитической системы прибора, дрейфом параметров электронного блока и другими причинами. Если для ВП использован вейвлет ^ ( t ) с двумя нулевыми моментами, то эта дрейфовая составляющая не отразится на результате преобразования выходного сигнала прибора.

Коэффициенты W(a, b) содержат комбинированную информацию как об используемом вейвлете, так и об анализируемом сигнале. Выбор анализирующего вейвлета определяется тем, какую информацию требуется извлечь из сигнала. Каждый вейвлет имеет характерные особенности во временном и частотном пространстве, поэтому с помощью разных вейвлетов можно полнее выявить или подчеркнуть те или иные свойства анализируемого сигнала.

Спектр W ( a , b ) одномерного сигнала представляет собой поверхность в трехмерном пространстве. Способы визуализации этой информации могут быть различными. Вместо изображения поверхностей часто представляют их проекции на плоскость ( a , b ) с изо-

t ²

V6 (t) = (- 6t6 + 15t4 - 45t2 + 15e"2;

t ²

V ( t ) = ( - 1 ⁷ + 21 t ⁵ - 105 t ³ + 105 t ) e "² ;

t ²

V₈( t ) = ( - t ⁸ + 28 t ⁶ - 210 t ⁴ + 420 t ² - 105 )e² •

линиями или изоуровнями, позволяющими проследить изменение амплитуд вейвлет-преобразования на разных масштабах и во времени. Несмотря на то, что коэффициенты вейвлет-преобразования содержат комбинированную информацию, вейвлет-анализ позволяет получить и объективную информацию об исследуемом сигнале, так как некоторые важные свойства вейвлет-преобразо-вания не зависят от выбора вейвлета.

Присутствие экспоненциального множителя в вейвлетах обеспечивает их локальность. Гауссов вейвлет v„ ( t ) имеет n нулей. Из определения гауссовых

вейвлетов следует, что производная от вейвлета

Vn (t)

В качестве вейвлетов будем использовать производные функции Гаусса:

совпадает (с точностью до знака) с вейвлетом

Vn+1(x ):

dV n ⁽ t )_ ... (Л d   ""^{Vn + 1 ( t} ) •

Вейвлетом может быть и разность функций Га усса. Обобщенная формула для этого вейвлета имеет

вид:

t ²

^V n ^{( t} ) = ^{( -} 1 ) n ⁺1 ^e ² >  n = ^0,1,2,... •

Наибольшее применение находят гауссовы вейвлеты небольших порядков:

t ²

V ₁ ( t ) = - te ² ;

t ²

V 2 ( t ) = ( 1 - 1 ² ) e ² ;

t ²

V3 (t) = (t3 - 31 )e 2 ;

V ( t ) = e ^{- At} 2

- Ce ^{- Bt} 2

;

a = B ;

C ²

ф vm)=xge-4A - c. ^ee

_т ²

4 B

•

Например, при

A = C = ^ B = 1

2 ’

получим:

t ²                t ²

V ( t ) = e ² - —e ⁸ •

V 4 ( t ) = ( - t ⁴ + 6 t ² — 3 ) e ^{2 ;}

t ²

V ₅ ( t ) = ( - 1 ⁵ +10 t ³ - 15 te ² ;

На выходе аналитических приборов регистрируются сигналы в виде локализованных пиков (см. табл. 1).

Таблица 1. Некоторые типовые модели аналитических пиков

Аппроксимирующая функция	Математическое выражение ( p - площадь пика; ц - положение пика на оси развертки; в - среднеквадратичная ширина пика)				Область применения
Гаусса	( t - ц ) 2 p   e  2 в 2 А /2 лв				Хроматография, масс-спектрометрия, рентгенодифракционный анализ
Лоренца	p пв	Г              1 1 ( t z £ ) l + 1 в 2			Спектроскопия, рентгенодифракционный анализ
Гиперболическая вида I	2 p ch		p п ( t - ц ) - 2 в		Полярография
Гиперболическая вида II	2pch2		Г4 - ц ) 2 в		Полярография

Для некоторых конкретных сигналов и вейвлет-функций возможно аналитическое вычисление непрерывного вейвлет-преобразования. Это позволяет по значениям вейвлет-коэффициентов определять информативные параметры пиков, входящих в состав исследуемого сигнала. Поскольку даже в случае зашумленных сигналов их вейвлет-образы имеют вид гладких кривых, возможно восстановление информативных параметров выходного сигнала прибора с достаточно высокой точностью.

Оценка параметров сигнала. Полезная со-

При z = 0 четные вейвлет-коэффициенты Wg2(а, b)5 и Wg4(а, b)5 имеют абсолютный мак симум, что может служит фактом обнаружения вершины пика в анализируемом сигнале. Обозначим максимальные значения вейвлет-коэффициентов W (а b)5 g 2

и W_g ( а , b ) 5 в максимуме через Q^ и Q ₄ . Решение

соответствующей системы уравнений дает оценки параметров /? и .А одиночного пика анализируемого

ставляющая выходного сигнала аналитического прибора в большинстве случаев может быть представлена в виде суперпозиции пиков, каждый их которых описывается гауссовой функцией [2,3]:

сигнала:

a

N    - s (t) =£ Ae

i = 1

( t - P i )²

2 р }

где i - номер пика, i = 1, 2,..., N ; A - амплитуда i -го

№ Ai I Q 4

А.

2 4 =

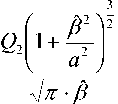
пика; ц - положение вершины i -го пика на оси раз

вертки t ; в - среднеквадратичная ширина i -го пика. Первичная обработка сигнала заключается в определении информативных параметров пиков: А ., ц , в , i = 1, 2,..., N .

Пусть анализируемый сигнал содержит одиночный пик с параметрами A , ц , Р . Вейвлет-образ этого пика при использовании гауссового вейвлета может быть вычислен аналитически и представлен в виде:

А л Пра ⁽ " ^{+ 1 )}

W g „ ⁽ a , ^b ) ⁵ =-------- g n ^{( z} ) ’

Следовательно, интегральная интенсивность (площадь) гауссова пика может быть найдена из соображе-

ния:

Ц - b          I 2 ,  ,,2

где z =------и т = л,/ а + р .

т

Формулы вейвлет-коэффициентов второго и четверто-

го порядков имеют вид:

W_{g 2}(а , b ) 5 = g 2

, ПАРа3 т3

Wg, ( а , b ) 5 = П^

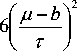
( ц - b ) ²

_ 2

( P - ь ) ² — ²

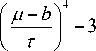
. ( ц - b ) ² e ^{2 т 2}

На рис. 1 и рис. 2 представлены графики соответствующих вейвлет-коэффициентов модельного сигнала с параметрами пика A =10 и Р =8.

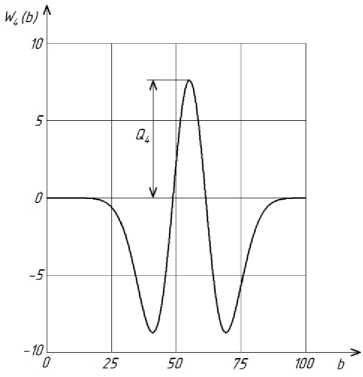
Рис. 1. Вейвлет-коэффициент четвертого порядка

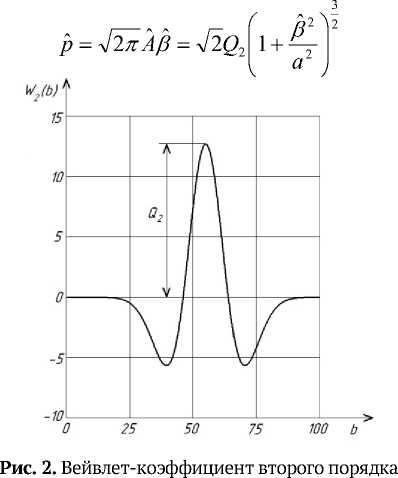
Рассмотрим результат восстановления аналитического пика гауссовой формы на основе метода вычисления его вейвлет-коэффициентов. На рис. 3 сплошной линией показан исходный пик; точками -восстановленный пик с использованием соотношений (6, 7). В случае одиночного пика имеем полное их совпадение.

Разделение совмещенных сигналов. Рассмотрим применение метода для разделения совмещенных пиков. На рис.1 представлен сигнал с двумя совмещенными пиками, а на рис. 2 его вейвлет-коэффициенты соответственно второго и четвертого порядка.

Для оценки параметров пиков необходимо использовать следующую процедуру. На основе анализа вейвлет-коэффициентов по формулам (6), (7) восстанавливается первый пик, который затем вычитается из исходного сигнала. К разностному сигналу применяется вейвлет-преобразо-вание второго и четвертого порядка, по максимальным значениям которых восстанавливается второй пик. Находим сигнал разности

между исходным сигналом и вторым пиком. Применяем к этому разностному сигналу вейвлет-преобразо-вания и находим уточненные оценки параметров первого пика. Описанные действия производятся до тех пор, пока разностный сигнал между исходным сигналом и восстановленными пиками не перестанет уменьшаться. Данная процедура позволяет полностью восстановить неразделенные пики за 6-7 итераций.

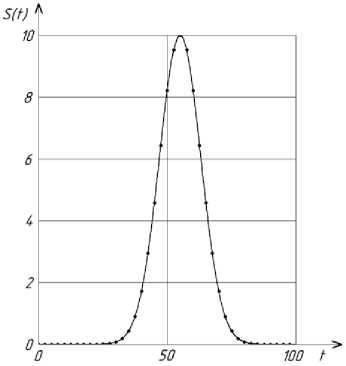
Рис. 3. Исходный и восстановленный пики: сплошная линия – исходный сигнал; ∙ ∙ ∙ – восстановленный сиг- нал

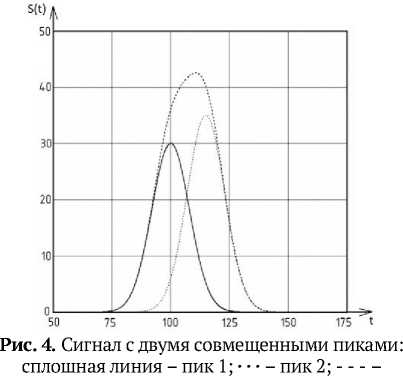
суммарный пик

ВД1

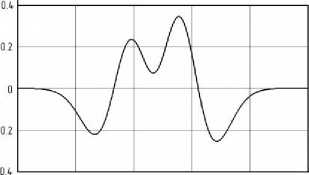
60          80          100         120 ЦО 160 t

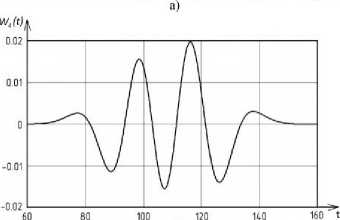
б)

Рис. 5 . Вейвлет-коэффициенты исходного сигнала: а – второго порядка; б – четвертого порядка

Выводы: Проанализирован метод первичной обработки сигналов аналитических приборов на основе их вейвлет-преобразования. Благодаря использованию заранее полученных формул расчета вейвлет-коэф-фициентов удается построить быстрые вычислительные алгоритмы обработки, что в сочетании с высокой их эффективностью является значительным достоинством метода.