Вейвлет-анализ временных рядов в модели кочевников и землепашцев

Описание данных

В работе [1] представлена агент-ориенти-рованная модель взаимодействия двух типов цивилизаций, которые условно были названы «кочевниками» и «землепашцами». Каждый тип агента олицетворяет собой цивилизацию с соответствующим способом воспроизводством продукта. Если землепашцы могут самостоятельно производить продукт для собственного потребления, то кочевники самостоятельно производить продукт не в состоянии, поэтому единственный способ добыть его чтобы выжить, это либо найти дикий ресурс, который с некоторой интенсивностью появляется на ареале, либо отобрать тот ресурс, который был произведен одним из землепашцев. В рамках построенной модели в работе [1] была проведена серия экспериментов, с помощью которой получен большой объем данных. На основе этих данных произведен статистический и эконометрический анализ, на базе которого удалось выявить ряд закономерностей. В данной работе также будет использован эконометрический подход, однако центральное место займет применение вейвлет-анализа, с помощью которого будут получены более сильные и статистически значимые закономерности.

Появление вейвлет-анализа можно датировать восьмидесятыми годами XX столетия.

Возникновение этого инструментария было вызвано необходимостью более чувствительного исследования сейсмических сигналов, в то время как используемый до этого метод Фурье не давал желаемых результатов. Вейвлет-анализ является мощной альтернативой классическому анализу Фурье. Новый метод также оказался применим в области теоретической физики и математике. Широкое применение вейвлет-анализ нашел в сфере обработки сигналов – очистка от шумов, сжатия данных и др. В настоящее время вейвлет-преобразование находит все более широкое применение в обработке временных рядов, будь это интернет трафик или биржевые котировки, распознавание образов и речи и др.

Существует много работ, в которых продемонстрировано применение вйвлет-пре-образований на практике. Применение вейвлетов в статистике и анализе временных рядов изложено в работах [4, 5], исследование финансовых временных рядов с помощью вейвлет-преобра-зований продемонстрировано в работе [6] и [8], также вейвлет–анализ активно применяется в технических дисциплинах, в таких областях как радиосвязь (обработка сигналов) [9], также для решения других прикладных задач технического характера [7] и [10, 11].

Приведем на графике данные по динамике численности популяций кочевников и землепашцев, а также динамику численности ресурса (рисунок 1 –3) .

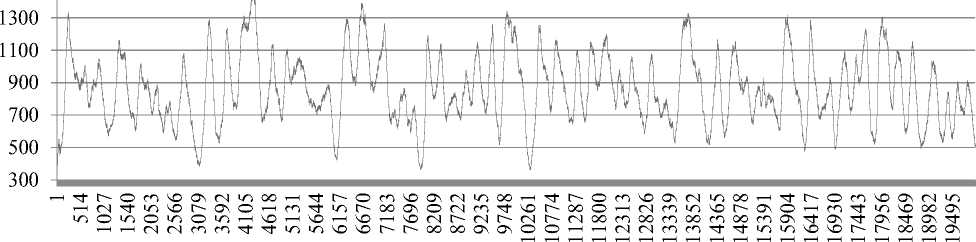
Рисунок 1. Численность землепашцев за 20000 периодов

Figure 1. The number of plowmen for 20000 periods

оооооооооооооооооо LTiOuriOuriOuriOuriOuriOuriOuriOuriO

ur>^^i^i^oooo^

Рисунок 2. Численность кочевников за 20000 периодов

Figure 2. The number of nomads for 20000 periods

Рисунок 3. Численность ресурса за 20000 периодов

Figure 3. The number of resource for 20000 periods

Таблица 1.

Корреляционная матрица

Correlation matrix

Table 1.

	кочевники | nomads	землепашцы | husbandmen	ресурс | resource
кочевники | nomads	1	-0.4138	-0.0023
землепашцы | husbandmen	-0.4138	1	-0.7986
ресурс | resource	-0.0023	-0.7986	1

Вейвлет-преобразования. Ортогональный кратномасштабный анализ

Продемонстрируем теоретические моменты применения вейвлет-анализа. Вейвлет-анализ аналогичен преобразованию Фурье, однако имеет свои особенности. Данную часть постараемся описать кратко, не сильно вдаваясь в детали. Иллюстрировать будем все на примере вейвлета Хаара. Здесь мы опишем принцип вейвлет-разложения для случая ортогональных вейвлетов.

Рассуждения, которые мы будем здесь приводить, будут справедливы для случая ор-тонормированных вейвлетов. Более подробно с этой теорией можно ознакомиться в частности в книге [2].

Определение. Функция v ( x ) e L ( R ) называется масштабирующей, если она может быть представлена в виде

v( x ) = 72 Е^( 2 x - n ), (1)

ne Z где числа hn, n e Z удовлетворяют условию

Е । h n I² < ^ю .

n e Z

Для каждого j e Z можно построить систему следующих функций Vj n (x) = V27v(2jx- n),n e Z, которая будет ортонормированной системой функций (напоминаем, мы рассматриваем случай ортогональных в L (R) вейвлетов). Для каждого фикси рованного j e Z такие функции являются ортонормированным базисом подпространства V , эти пространства в свою очередь образуют бесконечную в обе стороны последовательность вложенных подпространств „.с V с V с V с V „.с V с., причем такую, что ю                ю

Е V j = { 0 } и Е V j = L ( R ) .    (2)

j = - ю                 j = - ю

Для каждого из таких подпространств можно ввести операторы проектирования Pj : L ² ( R ) ^ V , которые с возрастанием j дают все более точные приближения P ( f )

элементов

Pj( f )=Е( f v n )vj n(x),

f e L ( R ) ,

neZ где (f ,^ „) — скалярное произведение в пространстве L ( R).

Число j характеризует уровень разрешения. Чем больше j , тем более мелкие носители имеют функции V к ( x ) и тем более детально коэффициенты ( f , V к ) отражают свойства f ^{( x} ) .

Отметим, что каждое подпространство V может быть разложено в прямую сумму ортогональных подпространств V = V ] Ф W^_ ]. Это разложение позволяет j -й уровень приближения P представить в виде суммы P ( f )= Pj i ( f ) + P W ( f ) • В базисах пространств V_jA и W имеем:

pj (f)(x)=Eaj-ik kV-i, k (x)+ k e Z

+Е^--i, k^j-i, k (x), k e Z ю      ________ где    aj-1,k = (f ,Vj-1,k) = J f (x)Vj-1,k (x)d[x -

-ю коэффициенты аппроксимации (j-1) – го уровня ю      _________ разрешения,  dj-1,k = (f,Wj-i,k) = Jf (x)^j-1,k(x)dx -

-ю детализирующие коэффициенты или коэффициенты детализации, {^j-1k } ^ - ортонорми- рованный базис пространства W

Очевидно, справедливо следующее разложение

P j ( f ) = P j - 1 ( f ) + j ( f ) =

.

= Pj-2 (f ) + PW2 ( f )+ j (f )

Такое разложение можно совершать итерационно N раз, тогда получим

N p,f=p, - k (. f )+ZPWk (f) • k=1

Вейвлет-анализ состоит из следующих шагов:

Выберем достаточно высокий уровень разрешения j , такой, что аппроксимация P ( f ) достаточно точно отражает функцию f . Если работа ведется с числовым рядом, то значения коэффициентов разложения для оператора P ( f ) приравниваются значениям рассматриваемого ряда.

Выбирается глубина разложения N и находятся коэффициенты разложения:

{ { a j - N , k ^{}   {} d j - N , k ^{}    { d} j - ( N - 1 ) , k ^} ’■••’ { d j - 1, k } } •

Масштабирующая функция вейвлета Хаара имеет вид

[ 1,    0 <  t <  1,

Ф н ( t ) = k

0,   иначе.

Очевидно условие (1) выполняется, так как

ф( x) = ф( 2 x) + ф( 2 x -1) =

( 1                   1

= ^I -/Тф(2x) + "7^ф(2x-1)

.

Соответственно h_Q = h = 1/ V2" , для остальных k e Z, k Ф 0 и k Ф 1 справедливо h = 0.

Очевидно, что для построенных с помощью такой масштабирующей функции подпространств Vj , j e Z условия (2) будут выполнены.

Определим {^j-k}^ z— ортонормирован- ный базис подпространства W , ортогонального пространству V . Не трудно видеть, что

Функция f ( x ) (или ряд) восстанавливается используя возможно измененные коэффициенты разложения:

f (x) = Eaj-N,k^-N,k (x) + k e Z

+Edj-N,k^-N,k (x) + ■ + EdH,k^j-1,k (x) • k e Z                            k e Z

^ j,k ( ^x )

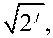
=^- 42 ,

0,

2 ^j x - k e

2 ^j x - k e

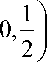
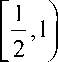
2j x - k £ [0,1)

В данной работе с помощью такого разложения мы будем корректировать рассматриваемые временные ряды. А именно, будут обнуляться коэффициенты детализации, соответствующие высоким частотам. Самые высокочастотные коэффициенты детализации - это {dj-1k } , следующие по высокоча- стотности коэффициенты –

^{ 4-²-^{k }} k e Z

и т. д.

После того, как несколько уровней коэффициентов детализации будут приравнены нулю (грубо говоря удалены «шумы»), исходный ряд будет восстановлен, но уже с учетом проделанной процедуры.

Вейвлет Хаара

Покажем работу алгоритма вейвлет-раз-ложения на примере самого простого вейвлета – вейвлета Хаара.

Видно, что функции ^j _k^ и Ф _k^ будут всегда ортогональны относительно скалярного произведения пространства L ( R ) при любых k и k ₂ ( k j ^ k ₂) из пространства Z .

Принцип действия проектора Pj (f) в случае вейвлета Хаара достаточно прост – на участках где ф к (x) не равна нулю коэффициенты a равны среднему значению функции f на этом участке сс           ______________

aj, k = (f, ф, k) = J f (x) Ф, k (x )dx =

-с

( k + 1 ) /2 ^j

= 42 J f (x) dx • k /2j

Аналогично определяются коэффициенты для оператора р ( f ) .

Для случая, когда у нас задан ряд {f }N вместо функции f , коэффициенты оператора P , (f) определяются с помощью правила арифметического среднего, примененного к коэффициентам оператора р (f). Так, если в соответствии с пунктом 1) вышеописанного алгоритма, в качестве коэффициентов оператора р (f) мы берем значения исходного ряда { f} N i,  тогда коэффициенты оператора р 1 (f) будут определяться по следующему правилу (не ограничивая общности будем считать, что N – четно)

{ a j - 1, к ^}

N /2

к = 1

a j ,1 + a j ,2   a j ,3 + a j ,4

2,2

a j , N - 1 + a j , N

I f + ^f i ^f 3 + ^f 4

I 2,2

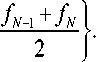
Коэффициенты оператора p^W ₁ ( f ) определяются по следующему правилу

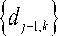
N /2

k = 1

a j ,1 ^- a j ,2   a j ,3 ^- a j ,4       a j , N - 1 ^- a j , N

2    ,    2     ..... 2

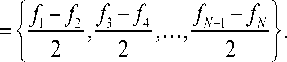
Аналогично, коэффициенты для операторов р __; ( f ) и p W ( f ) определяются итерационно через коэффициенты оператора P j - i + 1 (. f ) .

Соответственно восстановление коэффициентов проектора р __;+1 ( f ) осуществляется

через коэффициенты проекторов р _; ( f ) и p^W ( f ) по следующему правилу:

aj -i+1,2 к-1 = aj -i, к + dj -i,к , aj-i+1,2к = aj-i,к - dj-i,к.

Применение вейвлет-анализа к результатам работы модели «кочевников» и «землепашцев»

Применим вейвлет-анализ к временным рядам, которые были получены в результате работы модели «кочевников» и «землепашцев» (см. [1]). А именно, мы будем анализировать временные ряды численности популяций обоих видов, «кочевников» и «землепашцев». Кроме этого, в анализе также будет участвовать временной ряд, характеризующий количество ресурса (пищи), которое в каждый момент времени присутствует в рассматриваемом ареале. Применим вейвлет-анализ к этим данным и сделаем качественные выводы.

К рассматриваемым временным рядам будем применять различные вейвлет-преобра-зования с целью выяснения вопроса – какие вейвлеты подходят лучше для анализа изучаемых данных?

На первом этапе проведем простой эконометрический анализ исходных данных. На имеющихся данных методом наименьших квадратов оценим следующую регрессию:

y_t = в о + в 1 х 1 + в 2 x t + E _t ,       (3)

где y – количество землепашцев в рамках

1 ареале в каждый момент времени, x – количество кочевников в каждый момент времени, x ² – количество ресурса в каждый момент времени.

Длина временных рядов составляет равно 20000 периодов. Результаты применения регрессии видны в таблице 2.

Таблица 2.

Результаты регресси

Table 2.

Regression results

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
в о	2527,769	5,815146	434,6871	0	2516,3706	2539,1669
в 1	-2,20738	0,016166	-136,543	0	-2,239066	-2,175692
в 2	-3,25125	0,012416	-261,861	0	-3,275589	-3,226916

R ² = 0,81; DW = 0,94

Видно, что R ² достаточно большой, однако тест Дарбина-Уотсона показывает наличие автокорреляции первого порядка, что мешает использовать ее для прогнозов. Отметим также, что проанализировав порядок автокорреляции можно утверждать, что он на много больше чем один.

Проведем вейвлет-анализ данных после чего применим методы эконометрики.

После применения вейвлет-преобразования ко всем трем временным рядам обнулим высокочастотные коэффициенты детализации и восстановим исходные временные ряды с учетом обнуленных коэффициентов. После этого проведем эконометрический анализ модифицированных временных рядов.

Начнем с само простого вейвлета, а именно с применения вейвлета Хаара. Глубину разложения выберем равную N = 4.

Выясним какие результаты получатся, если сначала приравнять к нулю коэффициенты детализации первого уровня { d j - 1 _к }    = 0 .

На следующем шаге приравниваем коэффициенты детализации первого и второго уровней {dj-1,к }, 7 = 0 и {dj-2,к }, 7 = 0 и на тРетьем к £ z                    к £ z шаге приравняем нулю коэффициенты детализации первых трех уровней {dj-1 к }А = 0,

{ dj-2,к }, 7 = 0 и {dj-3,к }, 7 = 0 . На заключи-к £ z                    к £ z тельном шаге проведем анализ, приравняв все коэффициенты детализации нулю.

И так, приравнивая к нулю коэффициенты детализации на первом уровне { dj-\к }_{к z} = 0 , с учетом этого восстановим временные ряды и оценим регрессию аналогичную регрессии (3)

У. = в0 + в x + в2 xt + ^t.

Полученные результаты видны в таблице 3.

Приравняем коэффициенты детализации на первом и втором уровнях. Восстановив с учетом этого временные ряды и оценив регрессию получаем результаты, которые можно наблюдать в таблице 4.

На следующем шаге получаем результаты, изложенные в таблице 5.

На заключительном шаге имеем результаты, которые отражены в таблице 6.

Видим, что на каждом следующем шаге показатель R ² увеличивается, а статистика DW уменьшается. Увеличение R ² говорит об увеличении взаимозависимости исходных рядов, тогда как уменьшение DW свидетельствует об увеличении отрицательной автокорреляции.

Далее посмотрим, что изменится, если вместо вейвлета Хаара взять другие вейвлеты.

Рассмотрим вейвлет Добеши порядка 2. Как и в предыдущем случае глубину разложения возьмем равную N = 4. На первом шаге, приравняв { dj- ы}^ _г = 0 и восстановив временные ряды, имеем результаты таблицы 7.

На втором шаге, приравняв нулю следующий уровень коэффициентов детализации { d j - 1, к },= ^{0   и}   { d j - t, к L = ⁰ , получаем

X        У к £ Z                 X         У к £ Z результаты в таблице 8.

На следующем шаге, при {dj-1к } ^ = 0, { dj-2, к },7= 0   и   { dj -3, к },7= 0 , имеем к £ Z                         к £ Z результаты в таблице 9.

На последнем шаге, когда всех коэффициенты детализации равны нулю получаем результаты таблицы 10.

Таблица 3.

Результаты регресси

Table 3.

Regression results

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
А)	2615,36	5,1269	510,12	0	2605,3	2656,4
в 1	-2,2082	0,013959	-158,2	0	-2,2356	-2,1809
в 2	-3,4955	0,011113	-314,55	0	-3,5173	-3,4738

R ² = 0,86; DW = 0,46

Таблица 4.

Результаты регресси

Table 4.

Regression results

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
P 0	2675,61	4,5483	588,26	0	2666,7	2684,5
P l	-2,2091	0,012222	-180,75	0	-2,2331	-2,1852
P 2	-3,6634	0,009954	-368,03	0	-3,6829	-3,6439

R ² = 0,89; DW = 0,22

Таблица 5.

Результаты регресси

Table 5.

Regression results

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
P 0	2718,85	4,0489	671,51	0	2710,9	2726,8
P l	-2,2102	0,010794	-204,77	0	-2,2313	-2,47339
P 2	-3,7836	0,0089207	-424,14	0	-3,8011	-3,7661

R ² = 0,92; DW = 0,095

Таблица 6.

Результаты регресси

Regression results

Table 6.

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
P 0	2747,77	3,6645	749,84	0	2740,6	2755,0
P l	-2,2126	0,0097407	-227,15	0	-2,2317	-2,1935
P 2	-3,8629	0,0081143	-476,06	0	-3,8788	-3,8470

R ² = 0,93; DW = 0,045

Таблица 7.

Результаты регресси

Table 7.

Regression results

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
P 0	2612,51	5,1518	507,11	0	2602,4	2622,6
P l	-2,2087	0,014034	-157,39	0	-2,49752	-2,47339
P 2	-3,4872	0,01116	-312,48	0	-3,5091	-3,4653

R ² = 0,86; DW = 0,40

Таблица 8.

Результаты регресси

Table 8.

Regression results

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
P 0	2675,4	4,5512	587,84	0	2666,5	2684,3
P 1	-2,2087	0,012223	-180,71	0	-2,2327	-2,1847
P 2	-3,6631	0,009959	-367,82	0	-3,6826	-3,6436

R ² = 0,89; DW = 0,13

Таблица 9.

Результаты регресси

Table 9.

Regression results

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
P 0	2716,4	4,0843	665,09	0	2708,4	2724,4
P 1	-2,2081	0,010882	-202,92	0	-2,2295	-2,1868
P 2	-3,778	0,0089943	-420,05	0	-3,7956	-3,7604

R ² = 0,92; DW = 0,04

Таблица 10.

Результаты регресси

Table 10.

Regression results

	Коэффициенты Coefficients	Стандартная ошибка Standard error	t-статистика t-stat	P-Значение P-value	Нижние (lower) 95%	Верхние (upper) 95%
P 0	2743,5	3,7342	734,7	0	2736,2	2750,8
P 1	-2,212	0,0099155	-223,09	0	-2,2315	-2,1926
P 2	-3,8514	0,008257	-466,44	0	-3,8676	-3,8352

R ² = 0,93; DW = 0,01

Для вейвлетов Добеши с более высокими порядками и для других вейвлетов картина будет похожая. Таким образом исследование рассматриваемых временных рядов показало, что при удалении из временных ряда высокоча-стосных «шумов» с одной стороны взаимозависимость между этими данными увеличивается ( R ² увеличивается), с другой стороны наблюдается рост отрицательной автокорреляции ошибок. Наличие автокорреляции ошибок не позволяет нам использовать эту модель для осуществления прогнозов.

Заключение

Полученные результаты показывают, что проведенный вейвлет-анализ с одной стороны увеличивает коэффициент детерминации ( R 2 соответствующих регрессий стремится к 1), с другой стороны статистика Дарбина-Уотсона становится хуже, т. е. наблюдается усиление автокорреляции ошибок (в нашем случае DW-статистика стремится к 0). Можно отметить следующую закономерность – чем выше R 2 , тем ниже статистика DW. Наличие автокорреляции ошибок в регрессии не позволяет нам использовать построенные эконометрические модели для предсказаний, однако автокорреляция не мешает нам судить о характере зависимостей (метод наименьших квадратов в такой ситуации дает несмещенные и состоятельные оценки коэффициентов β , β и β ). Низкое значение статистики Дарбина-Уотсона может означать, что построенная модель учитывает не все значимые факторы.

Таким образом получаем, что количество землепашцев в каждый момент времени достаточно хорошо объясняется количеством кочевников и количеством ресурса на ареале. Однако количество землепашцев и количество ресурса содержит в себе не достаточно информации для того, чтобы по ним можно было предсказать количество кочевников. Удалив высокочастотные шумы с помощью вейвлет-анализа эта ситуация не меняется, а скорее даже усиливается.

При ближайшем рассмотрении такая ситуация видится вполне закономерной, поскольку помимо численности кочевников и ресурса на ареале свое влияние могут оказывать возраст агентов, соотношение дикого и культурного ресурса (культурный ресурс – ресурс, произведенный землепашцем), кроме этого влияние оказывают некоторые качественные характеристики такие, например, как взаимное