Вейвлетный анализ в обработке томографических изображений

При обработке томографических изображений актуальной представляется задача шумоподавления. Относительно новым является способ шумоподавления с помощью вейвлет-функций. Вейвлеты позволяют анализировать различные виды сигналов и эффективно устранять шум, поэтому особый интерес представляет исследование их возможностей для повышения качества изображений.

При обработке цифровых изображений чрезвычайно удобно использовать дискретное вейвлет-преобразование DWT (Discrete Wavelet Transform), т. к. оно обеспечивает наиболее глубокое проникновение к основным пространственным и частотным характеристикам [1–7].

МЕТОД ИССЛЕДОВАНИЯ

В данной работе рассмотрен метод шумоподавления с помощью различных вейвлет-функций, таких как вейвлет Хаара, симлет, койфлет, би-ортогональный вейвлет порядка N , обратный би-ортогональный вейвлет порядка N , вейвлет Мейера, вейвлет Добеши, модифицированный вейвлет Добеши [8–9].

Для обработки томографических изображений в формате DICOM (Digital Imaging and Cоmmunications in Medicine) с помощью методов вейвлетного анализа разработан алгоритм шумоподавления и его программная реализация. Алгоритм обработки изображений представлен на рис. 1 [1].

При разработке алгоритма примем: ϕ ( x ) — масштабирующая вейвлет-функция, ψ ( x ) — вейвлет. Они порождают базисные функции

ϕ _{j , n} ( x ) ϕ _{j , m} ( y ), ϕ _{j , n} ( x ) ψ _{j , m} ( y ),

ψ _{j , n} ( x ) ϕ _{j , m} ( y ), ψ _{j , n} ( x ) ψ _{j , m} ( y ).

Соответствующие коэффициенты определяются следующим образом. Аппроксимирующие коэффициенты сА j получаются как коэффициенты разложения по вейвлет-базису ϕ _{j , n} ( x ) ϕ _{j , m} ( y ) . Горизонтальные коэффициенты сH j получаются как коэффициенты разложения по вейвлет-базису ϕ _{j , n} ( x ) ψ _{j , m} ( y ) . Вертикальные детализирующие коэффициенты cV j получаются как коэффициенты разложения по вейвлет-базису ψ _{j , n} ( x ) ϕ _{j , m} ( y ) . Диагональные коэффициенты сD j получаются как коэффициенты разложения по вейвлет-базису ψ _{j , n} ( x ) ψ _{j , m} ( y ). Практически входной сигнал задается матрицей S. При разложении данного сигнала получаются указанные выше четыре типа коэффициентов.

Двумерное дискретное вейвлет-преобразование (ДВП) получается в результате применения одномерного преобразования последовательно к строкам и столбцам изображения. В результате мы получаем одну низкочастотную полосу и три высокочастотных, причем ВЧ-коэффициенты

Рис. 1. Алгоритм разложения двумерного сигнала при его обработке

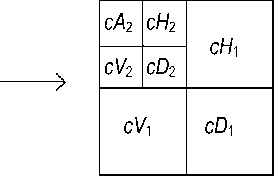
каждой полосы отвечают за конкретное направле- щью вейвлет-преобразования представлена на ние — вертикальное, горизонтальное либо диаго- рис. 2.

нальное. Общая схема шумоподавления с помо-

Рис. 2. Общая схема подавления шума на основе вейвлет-преобразования

Результаты расчетов PSNR и СКО

Вейвлет	Глубина разложения N
	N = 1		N = 2		N = 3
	PSNR, дБ	СКО	PSNR, дБ	СКО	PSNR, дБ	СКО
haar	33.70	111.32	33.78	109.27	33.24	123.85
sym2	34.17	100.05	35.40	75.36	34.34	96.15
sym4	34.18	99.81	35.80	68.68	34.74	87.75
sym8	34.18	99.76	35.98	65.84	34.79	86.64
coif2	34.17	99.86	35.91	67.00	34.78	86.94
coif4	34.17	99.85	36.01	65.39	34.80	86.44
bior2.2	34.11	101.39	35.82	66.44	34.97	83.13
bior4.4	34.14	100.67	35.99	65.74	34.72	88.17
rbio2.2	34.10	101.69	34.49	92.77	33.13	126.96
rbio4.4	34.14	100.75	35.57	72.45	34.65	89.42
dmey	34.17	99.88	36.07	64.49	34.81	86.20
db2	34.17	100.05	35.40	75.36	34.34	96.15
db4	34.17	100.07	35.93	66.63	34.72	88.03
db8	34.18	99.69	35.98	65.96	34.72	88.06
Мод. вейвлет Добеши Исход.	44.08	82.49	44.38	62.49	44.10	73.49
изобр.	31.17	199.57	31.17	199.57	31.17	199.57

ПРОГРАММНАЯ РЕАЛИЗАЦИЯ МЕТОДА ШУМОПОДАВЛЕНИЯ

Для решения задачи шумоподавления разработана компьютерная программа с использованием пакета системы Matlab — Wavelet Toolbox. Данный пакет включает в себя широкий набор инструментов по обработке, очистке, сжатию, визуализации сигналов и изображений.

Программа считывает из файла обрабатываемое изображение в формате DICOM (изображения были получены на магнитно-резонансном томографе General Electric Signa Infinity в СПбГУЗ "Городская Покровская больница"). После этого производится очистка изображения с целью устранения шума, который изначально присутствовал на данном изображении. Очищенное изображение принимается за эталонное, и в дальнейшем относительно него определяется степень очистки от шума. На очищенное изображение накладывается белый гауссовский шум и решается задача шумоподавления с использованием различных вейвлет-функций.

АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ

Выбор типов вейвлетов для проведения исследования основан на свойствах, которые имеют различные группы вейвлетов. Основными из них можно назвать поддержку дискретного вейвлет-преобразования и наличие масштабирующей функции ϕ .

Качество изображения определяется большим количеством технических характеристик системы: соотношением сигнал/шум и статистическими характеристиками шума, градационными характеристиками, спектральными (цветовыми) характеристиками, интервалами дискретизации и т. д. Для оценки качества обработки изображений наиболее часто используются такие критерии, как пиковое отношение сигнал / шум PSNR (англ. Peak Signal-to-Noise Ratio) и среднеквадратическое отклонение (СКО). Поэтому в программе производится расчет пикового отношения сигнал/шум (PSNR) и СКО яркости пикселей обработанного изображения по сравнению с эталонным изображением. Исходное, эталонное, зашумленное и обработанное изображения, а также результаты расчетов PSNR и СКО выводятся на экран.

Результаты расчетов PSNR и СКО представлены в таблице. Анализ этих данных показывает, что шумоподавление достигается при всех исследованных уровнях разложения и при всех рассмотренных вейвлет-функциях. Наилучшие результаты шумоподавления были достигнуты при глубине разложения, равной двум ( N = 2).

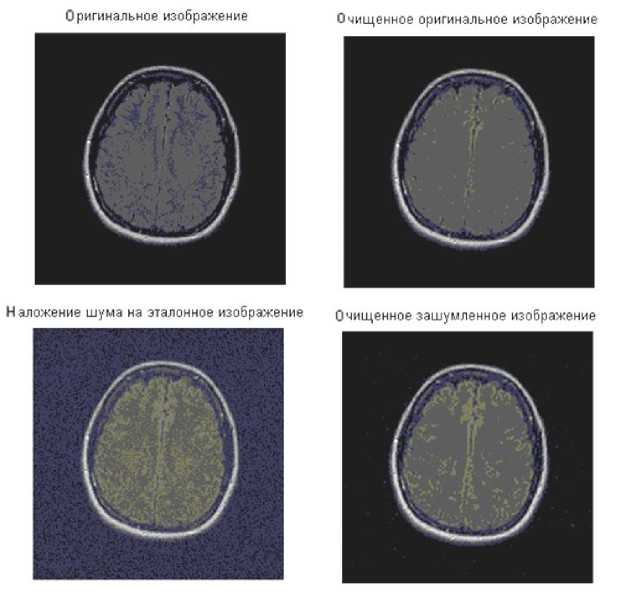
Рис. 3. Очистка вейвлетом Мейера при глубине разложения N = 2

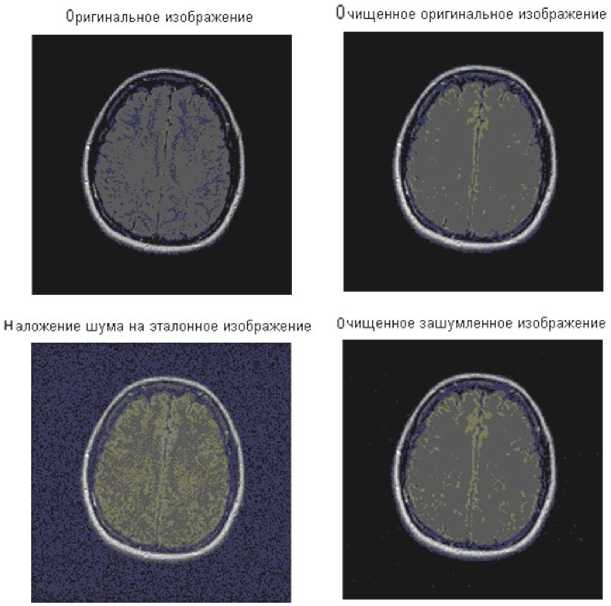
Рис. 4. Очистка модифицированным вейвлетом Добеши при глубине разложения N = 2

Использование глубины разложения больше трех не рекомендуется, т. к. глубина разложения влияет на размер отсеиваемых деталей [6–7]. Другими словами, при увеличении глубины разложения программа вычитает шум все большего уровня, пока не наступит "переукрупнение" масштаба деталей и преобразование не начнет искажать форму исходного сигнала. При дальнейшем увеличении глубины разложения преобразование начинает формировать сглаженную версию исходного сигнала, т. е. отфильтровывается не только шум, но и некоторые локальные особенности (выбросы) исходного сигнала. В этом случае происходит не только подавление шума на изображении, но и сглаживание изображения (изображение принимает размытый вид). При анализе показателей шумоподавления в зависимости от вида вейвлет-функции наилучшие результаты показали дискретный вейвлет Мейера (dmey) и модифицированный вейвлет Добеши. Результаты обработки данными вейвлетами при глубине разложения N = 2 представлены на рис. 3 и 4.

ВЫВОДЫ

Анализ экспериментальных данных показал, что из рассмотренных в работе вейвлет-функций для решения задачи шумоподавления в томогра- фии наиболее подходят вейвлет Мейера (dmey) и модифицированный вейвлет Добеши. Наилучшие показатели шумоподавления достигаются при глубине разложения N = 2.

Разработанные методы обработки изображений могут быть использованы для определения оптимальных способов применения вейвлет-функций при решении задач повышения качества изображений. Также результаты данной работы могут быть использованы при конструировании фильтров, основанных на вейвлет-функциях.

Исследования, описанные в статье, осуществлены при поддержке Российского фонда фундаментальных исследований, грант № 08-08-00922а.