Вейвлеты с конечной замкнутой формой представления
Автор: Малыхина Г.Ф., Меркушева А.В.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Оригинальные статьи
Статья в выпуске: 3 т.14, 2004 года.
Бесплатный доступ
Преобразование нестационарного сигнала в информационно-измерительных системах для анализа динамического спектра основано на применении вейвлетов (совокупности масштабирующей- и вейвлет-функций, образующих базисы подпространств различного масштаба, группы фильтров и алгоритмов организации этой совокупности в систему). Построение компонент обычных вейвлетов включает бесконечные произведения и суммы, в связи с чем они не имеют замкнутого представления и для реализации требуют базовых вычислений, включающих аппроксимации. Нами рассмотрены метод, процедуры и практическое построение вейвлетов, имеющих замкнутую форму представления.
Короткий адрес: https://sciup.org/14264353
IDR: 14264353 | УДК: 621.391;519.21
Текст научной статьи Вейвлеты с конечной замкнутой формой представления
Почти все известные ортонормальные вейвлеты, кроме простейших (и сейчас практически не применяемых) вейвлетов Хаара и Шеннона, не могут быть выражены в конечной замкнутой форме. Под таким видом выражения имеется в виду представление вейвлетов в виде явной зависимости от элементарных (тригонометрических, экспоненциальных, дробно-рациональных) функций или от более специальных функций математической физики (гамма, Бесселя). Суть проблемы в том, что основная часть вейвлет-преобразований, которые позволяют анализировать структуру нестационарных сигналов в информационно-измерительных системах ( ИИС), базируется на вейвлет-базисах (вейвлетах), получение которых связано с построением бесконечных произведений, их преобразованием Фурье, конечными аппроксимациями, табулированием передаточных функций фильтров и разработкой программных средств, которые включены в некоторые пакеты (в виде так называемых toolbox’ов) [1]. Однако существуют процедуры для получения вейвлетов в замкнутой форме (в упомянутом выше смысле), и эта форма может быть использована для их непосредственного вычисления. Процедуры позволяют получить как ортогональные вейвлеты, так и неортогональные (но интерполирующие) вейвлеты.
Вейвлет-преобразования (ВП) находят применение при решении широкого круга задач: от обработки нестационарных сигналов в ИИС (для получения динамического спектра) до ряда областей математики (уравнения в частных производных и операторные), физики (область элементарных частиц высоких энергий) и биологии (диагностика на основе анализа структуры процессов) [2–4]. Это связано с тем, что вейвлеты образуют базисы сигналов или пространственных и временных функ- ций обширного класса, обладают уникальным свойством экономного представления и локализации любых особенностей сигнала, сжатия информации, воспроизведения исходного сигнала без искажений. Тем не менее почти все ортонормиро-ванные вейвлеты не могут быть выражены в замкнутой форме [5, 6]. Так, построение наиболее часто используемых вейвлетов Добеши (Daubechies), имеющих важное свойство ортонормальности и компактной области определения, получается на основе поиска тригонометрического полинома m(t) с определенными свойствами. Полином m(t) определяет частотную форму масштабирующей функции ВП, а степень m(t) — меру регулярности (гладкость, определяемую числом непрерывных производных) масштабирующей функции и связанной с ней вейвлет-функции. А именно эти две функции ВП определяют структуру так называемого многоразрешающего анализа (multi-resolution analysis) сигналов и функций, т. е. представление на разных уровнях масштаба в виде аппроксимаций и их остатка (в форме деталей). Масштабирующая функция (МФ) φ(t) получается как обратное преобразование Фурье (ПФ) от ее частотного представления ϕˆ :
ϕ ˆ( ω ) =
∞
∏ m (2 - kω ).
k = 0
После того как масштабирующая функция найдена, вейвлет-функция (ВФ), порождающая вейвлет-базис, определяется по одному из выражений: (2) — для частотной формы ВФ или (3) — для временнóй формы:
ψ ˆ( ω ) = e - ω /2 m ˆ( ω /2 + π ) φ ˆ( ω /2), (2)
∞
ψ ( t ) = ∑ ( - 1) nh - n + 1 (2 t - n ), (3)
n =-∞ где {hn}+“ в (3) являются коэффициентами в представлении m (го) рядом Фурье: m (to) = те
= (12) У !' .
Пос n кольку явный вид обратного ПФ от бесконечного произведения (1), приведенного выше, получен быть не может, то замкнутой формы выражений для вейвлетов Добеши неизвестно.
Близкий (с вейвлетами Добеши) по значимости — это вейвлет Мейера (Meyer), образующей которого служит единственная функция (4), т. к. логика конструкции Мейера требует от нее бесконечной гладкости (дифференцируемости) и компактности области определения:
ф( го ) =
exp( - 1/(1 - го 2)),
0,
I го | < 1;
иначе.
Обратное ПФ от < р ( ш ) в виде (4) тоже не представляется в замкнутой форме, поэтому и вейвлет Мейера не имеет конечной замкнутой формы.
Существование полноценного ортонормиро-ванного базиса ВП с аналитическим представлением МФ и ВФ, которые могут вычисляться явным образом через элементарные или хорошо известные специальные функции, было установлено Вальтером (Walter) [7, 8]. Им найдено два класса таких вейвлетов, названных вейвлетами приподнятого косинуса.
(Можно отметить, что один из видов этих вейвлетов использовался ранее в цифровой связи в виде импульсов, имеющих спектр приподнятого косинуса, для удаления межсимвольной интерференции)
Прототип масштабирующей функции первого класса определяется выражением
Ф 1 ( t ) =
sin(1 - в ) t + 4 в t cos п (1 + в ) t nt [1 - (4 в t )2]
где 0 < в < 1/3. Связанная с этой МФ основная вейвлет-функция имеет вид
V 1 ( t + 1/2) =
= sin п (1 + в ) t - 4 в t cos п (1 - в ) t
- пt [(4 вt )2 - 1]
sin2 п (1 - в ) t + 8 в t cos 2 п (1 + в ) t п t [(4 в t )2 - 1]
Другой класс вейвлетов приподнятого косинуса рассмотрен ниже.
Для анализа использованных Вальтером методов и процедур целесообразно сначала остановиться на элементах ВП, ряде используемых ниже обозначений и функций, которые входят в замкнутые выражения аналитических вейвлетов.
ВСПОМОГАТЕЛЬНЫЕ ОБОЗНАЧЕНИЯ И ЭЛЕМЕНТЫ ПРИКЛАДНОЙ ТЕОРИИ ВЕЙВЛЕТОВ
Будем считать, что отсутствие пределов у интегралов соответствует их значениям -те , + те ; У к означает суммирование по к в пределах -те , + те ; символ ф — это ПФ от функции ф (т. е. ее представление в частотной форме); все сигналы и функции имеют ограниченную L2-норму (конечную энергию, интеграл квадрата модуля); принадлежность сигнала или функции к L1 означает интегрируемость ее модуля; Z — множество всех целых чисел (<0, 0 и >0).
ПФ s(to ) сигнала s ( t ) и его обратное преобразование Фурье связаны соотношениями
s(го ) = f s ( t ) eJ to t d t и s ( t ) = — [ s(го ) e J to t d го . (7) 2 π
Непрерывная функция S считается функцией отсчетов (или интерполирующей), если она удовлетворяет двум условиям:
-
1) S ( n ) = 5 n ,0 n = 0, ± 1, ± 2, ... и
-
2) Существуют постоянные A и B >0 такие, что для всех значений ω
0 < A < У k\S (го + 2 пк )|2 < B <те .
В частности, эти условия выполняются для широко известной в области обработки сигналов sinc-функции (функции отсчетов), которая имеет вид: sin( πt )/( πt ) и представляет из себя масштабирующую функцию вейвлета Шеннона. (Заметим, что условие 2) делает { S ( t-n )} n=-∞…+∞ так называемым базисом Рисса).
В основе вейвлет-преобразования лежат ВФ [6, 9], которые образуют универсальные базисы {ym , n ( t )} m ,n , хорошо приспособленные к обработке нестационарных сигналов и анализу динамических спектров:
ym,n(t) = 2m/21/ (2mt - n); m, n — целые, (8) где у/" является основной функцией, образующей базис. Функция у имеет несколько разновидностей, каждая из которых обладает одной из несовпадающих групп полезных свойств. Это делает выбор у (и, следовательно, всего базиса) зависимым от контекста решаемой задачи обработки сигнала. Набор функций вейвлет-базиса должен быть либо ортонормальным (с взаимно ортогональными и нормированными компонентами ба- зиса), либо принадлежать к классу базисов Рисса [5].
Обычно ВФ формируются посредством первоначального построения МФ. Эти МФ должны удовлетворять определенным свойствам, которые позволяют выполнять многоразрешающий анализ, т.е. представление сигнала на нескольких уровнях масштаба, являющихся мерой разрешающей способности наблюдения частотной структуры нестационарного сигнала. Строго говоря — это структура сигнала на нескольких уровнях масштаба его представления. Однако, поскольку параметр масштаба a = 1 /ю, то это является и частотным представлением с гиперболической (1/ ю ) шкалой частот.
Свойства, которым должны удовлетворять МФ вейвлет-преобразования, могут быть представлены как во временной области (9):
J ф(t ) ф ( t - n )d t = 5 о, п , n — целое ( n e Z, Z — решетка целых на вещественной оси);
Ф ( t ) = У c k Ф (2 t - k )’ { c k } k e Z e 1 2;
k для любого сигнала f (t)
f m ( t ) = ^ а тп ф(2 m t - П ), f m ( t ) f ( t ) (9)
n m
m ( to /2) является 4 п периодичным расширением от Ф ( ю ), и, следовательно, выполняется соотношение
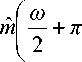
ф ^^ I 2 J
1 ,
0 ,
п < |to | < 2 п ;
иначе .
Это приводит к ВФ Шеннона в форме выражения
V ( t ) =
sin 2 п ( t - 1/2) - sin п ( t - 1/2)
п ( t - 1/2)
— так и в виде эквивалентного набора (1о) свойств в частотной области:
У k 1 Ф ( » + 2 nk )|2 = 1,
Ф to ) =f 1 У c j /2 ) Ф ( ® /2) =
I 2 )
= m(to /2) ф ( to /2),
Кроме приведенных элементов связи МФ и ВФ в теории вейвлетов и иллюстрирующего примера ВФ Шеннона, до выполнения процедуры получения вейвлетов с замкнутой формой мы предварительно сформулируем положение, которое определяет необходимое и достаточное условие того, чтобы некоторая функция S была функцией отсчетов и как из частотной формы такой функции может быть получена МФ другого вейвлета. Более строго: для S и S e L1 S будет являться функцией отсчетов (т.е. S ( n ) = 8 n 0), если (и только если)
те выполняется условие У S(to + 2kп) = 1. Причем k=-те при S(to) > 0 функция S порождает ортонормальное семейство функций {фп (t) = (t - n)} neZ, Фп (t) e L2, где фп (t) является временной формой масштабирующей функции ф(to) = д/S(to).
где m ( to /2) = 2- у k c/0* /2 ю = 0 и ф (0) = 1.
Ф непрерывна при
По полученной МФ строится основная ВФ. ВФ тоже может быть определена как во временной области, так и в частотной. Во временной области для этого используется соотношение
V ( t ) = У k ( - 1) k + 1 С 1 - k (2 1 - k ). (11)
В связи с формой зависимости ВФ от МФ это выражение называют уравнением растяжения. Частотная форма основной вейвлет-функции имеет вид
V ( to ) = ej m /2 m ( to /2 + п ) ф ( to ).
Частотная форма МФ вейвлета Шеннона является характеристической функцией интервала [-п, п ]: ф ( to ) = х [ - пп ] ( to ). Согласно выражению (8),
ПРОЦЕДУРА, ПОРОЖДАЮЩАЯ ЗАМКНУТУЮ АНАЛИТИЧЕСКУЮ ФОРМУ
ВЕЙВЛЕТОВ
В основе процедуры лежит функция h со свойствами: h > 0, четная ( h ( -x ) = h ( x )), нормированная ( J h ( x )d x = 1) и имеет в качестве области определения интервал [- п /3, п /3]. (В связи с особой ролью функции h используют понятие h -процедуры). Функция h , проинтегрированная на интервале 2 п , эквивалентна ПФ (или частотной форме) некоторой масштабирующей функции ф ( ю ), т.е. имеет место соотношение
ф ( to ) = J h ( x )d x , (13)
ю-п где ф)(ю)> 0 — четная, непрерывная функция, имеющая в качестве области определения интервал [-2п/3, 2п/3] и удовлетворяющая условию
те
^ ф( го + 2 кп ) = 1.
к —-те
Обратное ПФ (временная форма ф ( t )) является масштабирующей функцией и одновременно функцией отсчетов. Соответствующая ей ВФ представляется с помощью выражения
^ ( t + 1/2) = 2 ф (2 t ) - ф ( t ). (15)
Эта ВФ в силу (15) и приведенного выше условия является функцией отсчетов на полуцелых значениях аргумента
V ( n + 1/2) = 5 „ ,о . (16)
Описанная процедура для образования < р ( го ) может быть использована для получения частотной формы некоторой новой ортогональной МФ Ф-Ло ):
ф 0 (го ) = V ф(го ) , (17)
где ф0(го ) удовлетворяет условиям, которые необходимы для МФ вейвлет-преобразования и выражены в частотной форме (10).
Метод такого подхода введен Лиу (Liu) (см. [10] и [11]) и позволил ему получить масштабирующие функции, которые являются одновременно и ортогональными, и функциями отсчетов, т.е. удовлетворяют условию второго соотношения в (10) ("уравнению сжатия") и условию (14). Одна из полученных таким образом масштабирующих функций в замкнутой форме [7] приведена выше (5), вторая может быть выражена соотношением
. . sin п(1 - в)t + sin п(1 + в)t ф") (t) —
-
2 2 п t [1 + 2 в t ]
Этот принцип порождения новых видов вейвлетов из уже полученных МФ можно реализовать путем использования в качестве первичных такие вейвлеты, как sinc-функцию и два вида приподнятого косинуса (5) и (18).
Первичный вейвлет — sinc-функция
Частотная форма МФ для sinc-функции представляет характеристическую функцию интервала [- п , п ], а е(го) может быть принята в виде кусочнопостоянной функции. Такая е(го) не удовлетворяет условию непрерывности в нуле, но она (как легко проверить) может быть использована аналогично функции h , включая формулу (13). Соответствующая функция m d (to) тоже будет кусочнопостоянной, 2 п -периодичной и (при условии | m ( го ) |2 + 1 m ( го + п ) |2 — 1) дополнительно удовлетворяет соотношению
| m е ( го )|2 + 1 m е ( го + п )|2 — 1. (19)
Причем имеет место встречная импликация (тогда и только тогда):
I т е ( го ) |2 + 1 m е ( го + п ) |2 — 1 ^
^ | m ( го ) |2 + 1 m ( го + п ) |2 — 1.
Это позволяет вывести ряд вейвлетов, имеющих замкнутую форму выражения.
Общий набор процедур
Этапы реализации описанного метода формирования вейвлетов в замкнутой форме включают набор процедур, для которых нужно ввести ряд обозначений.
-
• Для целого n > 0 вводится набор полуоткрытых (справа) интервалов:
ОРТОГОНАЛЬНЫЕ ВЕЙВЛЕТЫ В ЗАМКНУТОЙ ФОРМЕ
Ортогональные вейвлеты более общей формы могут быть получены на основе метода Вальтера [10], который ввел способ модификации ортогональной МФ ф ( t ), позволяющий получить новый ортогональный вейвлет-базис масштабирующей функции. Им показано, что, используя МФ ф ( t ), ее ПФ <р(го ) и нечетную, непрерывную в нуле функцию е ( го ), для которой е ею является 2 п -периодичной, можно образовать новую МФ ф е ( го ) — в^ го ф(го ). Эта частотная форма ф е ( го ) новой МФ будет удовлетворять условиям (8), а обратное ПФ от нее ф е ( t ) является также ортогональной МФ. Т.е. ф е ( t ) образует ортогональный базисный набор {ф 6 ( t - n )} n e z .
I
0 —
0, п 2 n
,
к — 1,2,..., n .
I k
π
2 n - к + 1
)
n - к 2 7
,
-
• Определяется е 1 (го) на интервале [0, п ]:
е 1 (го) = Ек для го е 1к , к = 1,2,..., n.
-
• В качестве е (го) берется нечетное продолжение е 1 (го) на интервал [- п , п ] и его периодическое продолжение на всю вещественную ось (-да, го).
Определенная таким образом функция е ( го ) удовлетворяет условию (19) и порождает ф е ( го ) и ф е ( t ). Причем { ф е ( t - n )} n e Z является ортонормальным базисным набором на L2 (с элементами базиса, интегрируемыми с квадратом), а ф е ( t ) удовлетворяет уравнению растяжения (второе со-
отношение в условиях (9)).
Если в качестве E k используются значения, кратные п (например, 0 и п), то ф е ( ю ) — вещественная. И как можно показать [12], в этом случае функция т е (ю/2~) — четная, и представляет собой расширение на 4 п -периодичную модификацию, получаемую из функции т е ( ю / 2) вида
г
где ак = п
V
2 n - к + 2 - 1 А
2 n - к + 1
к = 1,2,..., n + 1.
ПРИМЕНЕНИЕ ПРОЦЕДУР ВАЛЬТЕРА ДЛЯ ПОЛУЧЕНИЯ ВЕЙВЛЕТ-ФУНКЦИЙ В ЗАМКНУТОЙ ФОРМЕ
на
I 0 ;
m е ( ю /2) = -
ej ( E k -E k - i )
на I k , к = 1,2,..., n ; (21) на [ п ,2 п ).
Частотное представление вейвлет-функции (ее ПФ) может быть получено с помощью (12) и цепочки соотношений:
V9 ( ю ) = e /2
mθ
ω
= e j Е ® /2 - е ( ® + 2 п ) + е ( to /2 + п )]
—+ п
Ф е
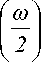
а Г ю А
л
т е\— + п Ф е
V 2 7
ω
\
e j [ ® /2 - е ( ® + 2 п ) + е ( ® /2 + п )]
j ® /2 а ej mθ
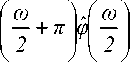
С учетом указанных выражений преобразование Фурье ВФ определяется формулой
e к а к ,
если A;
e - j ( ® /2) V/(ю) = ■
e E ka 0 ,
если B; (23)
0,
если иначе;
В общем виде описанный метод и последовательность процедур, позволяющие строить аналитические вейвлеты, представляет достаточно сложное построение. Его общность определяется возможностью широкого выбора для величины n и значений параметров Ек . В связи с недавним появлением самого метода совокупность ВФ этого типа пока не исследована; объем всего класса обширен, но строго не установлен. Тем не менее представляется полезным проследить схему построения вейвлетов в замкнутой форме с помощью рассмотренных процедур для небольших значений n и величин параметров Ек , которые наиболее удобны при расчете.
Для n = 1, I 0 = [0 , п /2), I j = [ п /2, п ) положим Е о = 0, тогда, если выбрать значение Е | = 0, то можно получить sinc-функцию. Значение Е 1 = п при прежней величине остальных параметров процедуры (в соответствии с выражением ак = ej ( Е к -Е к ' ) и соотношением из (24)) дает а 0 = 1; а 1 = -1; а 1 = = 3п/2 и а 2 =п . Поэтому вейвлет-функция для таких условий будет иметь вид
A:
1 Г_ 1 А
п I 2--- < | ю | < п I 2-- — I , к = 1,2,..., n ;
n - к 1 1 n- - к + 1 ’ ’ ’ ’ ’
V 2 7 V 2 7
у ( t ) = -( - 1)- х п ( t - 1/2)
х { sin 2 п ( t - 1/2) + sin п ( t - 1/2) - 2 sin[(3 п /2)( t - 1/2)] }
B:
п \ 2
1 А
V 2 n где а о = 1,
< | ю | < 2 п ,
ак = ej ( E k -E k - 1 )
к = 1, 2, ..., n.
Процедура получения основной вейвлет-функции заканчивается выполнением обратного преобразования Фурье от i / ( ® ). После проведения
Для n = 2, I о = [0, п /4), I j = [ п /4, п /2) и Iг = [ п /2, п ) положим е 0 = 0, тогда имеется три возможных случая.
— При значениях Е 1 = 0 и е 2 = п получается рассмотренная выше ВФ.
— При Е 1 = Е 2 = п получаются оценки а 0 = 1, а 1 = - 1, а 2 = 1 и тогда, согласно (23), получается выражение
ряда необходимых для этого преобразований получается ВФ в замкнутой форме в виде выражения
V ( t ) =
± 1 --------х п ( t - 1/2)
х { sin 2 п ( t - 1/2) +
- 1
при
7 п/ 4 < | ю | < 2 п ;
e " j ( ® /2) 1V (ю ) = ■
1
при
3 п/ 2 < | ю | < 7 п /4;
- 1
при
п < | ю | < 3 п / 2;
0
в других случаях.
n
+ У ( а к - а к - 1 )sin а к ( t - 1/2) -
к = 1
- a n sin а n + 1 ( t - 1/2) } (24)
Поскольку для этого варианта параметров получаются значения а 1 = 7 п/ 4; а 2 = 3 п/ 2 и а3 = п, то непосредственным преобразованием может быть определена ВФ в виде выражения
V ( t ) =
п ( t - 1/2)
x
-
x { sin п ( t - 1/2) - 2 sin[(3 п / 2)( t - 1/2)] + + 2 sin[(7 п / 4)( t - 1/2)] - sin 2 п ( t - 1/2) } .
— При E 1 = n; e 2 = 0 получаются оценки a о = 1, a 1 = a 2 = – 1.Тогда на основе (23) определяется выражение для частотной формы ВФ
e ~j( - /2) V(ro ) = J- 1
при 7 п /4 <\ro | < 2 п ;
при n < | ro | < 7 п /4;
в других случаях.
И аналогично предыдущему варианту путем обратного ПФ получаем ВФ
V ( t ) =
п ( t - 1/2)
x
x {sin 2 п ( t - 1/2) + sin п ( t - 1/2) -
- 2sin[(7 п /4)( t - 1/2)]} .
ЗАКЛЮЧЕНИЕ
По принятой в области обработки сигналов (Signal processing) терминологии вейвлетами называют совокупность компонент вейвлет-прео-бразования: масштабирующую функцию и основную (материнскую) вейвлет-функцию (порождающую вейвлет-базис с помощью аффинного преобразования временнóго или пространственного аргумента ВФ) и концепцию мультимасштабно-го анализа — анализа частотной структуры исследуемого сигнала на различных уровнях масштабов. По логике построения ВФ (т.е. последовательности МФ — m -функция — ВФ) структура вложенных подпространств различного масштаба формируется путем дискретного бинарного растяжения оси времени у МФ и создания локального базиса в каждом из таких подпространств набором МФ с определенным шагом временнóго смещения. Технология построения включает математические преобразования с бесконечными произведениями и суммами, использование аппроксимаций, вычислительной фазы, организации алгоритмов с программной их реализацией и использование в Toolbox прикладных систем Matlab, Matcad, Mathematica. В связи со столь сложной методологией построения у всех вейвлетов (кроме двух примитивных видов) отсутствуют конечные замкнутые выражения.
В отличие от вейвлетов, доступных для практического использования только в форме пакетов указанных выше систем, сравнительно недавно (94–98 г.) разработаны вейвлеты с замкнутой фор- мой представления, которые дают возможность непосредственного вычисления, практически не требуют аппроксимаций, могут использоваться в схеме мультимасштабного ("многоразрешающего") анализа нестационарных сигналов ИИС без построения фильтров. В статье рассмотрены метод, процедуры и практическое построение вейвлетов, имеющих замкнутую форму представления.
В силу новизны методов и процедур получения вейвлетов с аналитической формой (они разработаны на десятилетие позднее появления теории вейвлет-преобразования) многообразие класса таких вейвлетов пока не полностью исследовано, а систематизация их еще только предстоит.
Список литературы Вейвлеты с конечной замкнутой формой представления
- Дьяконов В.П., Абраменкова И.О. Matlab 5.0/5.3. Система символьной математики. СПб.: Питер, 1999. 633 с.
- Кратиров Д.В., Меркушева А.В. Алгоритм, основанный на вейвлет-преобразовании и нейронной сети, для бесконтактного измерения параметров газожидкостного потока//Сборник докладов Международной конференции "Датчики и системы". СПб.: Изд. СПбГТУ, 2002. Т. 3. с. 51-55.
- Малыхина Г.Ф., Меркушева А.В. Вейвлет-фильтрация нестационарного сигнала с адаптацией на основе нейронной сети//Труды Международной конференции по мягким вычислениям и измерениям SCM-2001. СПб.: СПбГЭТУ, 2001. т. 1. с. 239-242.
- Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование//Успехи физических наук. 2001. т. 171, № 5. с. 465-501.
- Daubechies I. The wavelet transformation, time-frequency localization, and signal analysis//IEEE, Transactions on Information Theory. 1990. v. 36. p. 961-1005.
- Чуи К. Введение в вейвлет. М.: Мир, 2001. 412 с.
- Walter G., Zhang J. Orthonormal wavelets with simple closed-form expressions//IEEE, Transactions on Signal Processing. 1998. v. 46. p. 2248-2251.
- Walter G. Translation and diliation invariance in orthogonal wavelets//Applied computations and harmonic analysis. 1994. v. 10. p. 344-349.
- Меркушева А.В. Классы преобразований нестационарного сигнала в информационно-измерительных системах. Время-масштабные (вейвлет-) преобразования для спектрально-временного анализа//Научное приборостроение. 2002. Т. 12, № 3. с. 68-82.
- Walter G. Wavelets and other orthogonal systems with applications. CRC Press, Boca Raton, FL, 1996. 230 p.
- Hernandez E., Weiss G. A Course on Wavelets. CRC Press, Boca Raton, FL, 1996. 189 p.


