Векторизация метода распространяющегося пучка и его реализация по технологии CUDA

Развитие оптических технологий определяет необходимость совершенствования известных и создания новых методов моделирования распространения электромагнитного излучения. В области волоконной и интегральной оптики получили широкую известность варианты метода распространяющегося пучка (BPM – Beam propagation method): Fast Fourier transform Beam propagation method (FFT-BPM) [1], Method of lines Beam propagation method (MoL-BPM) [2], Finite-difference Beam propagation method (FD-BPM) [3], Finite elements Beam propagation method (FE-BPM) [4], модифицированный метод распространяющегося пучка [5]. Объединяет упомянутые варианты дискретизация функции амплитудно-фазового распределения поля и численное решение уравнения Гельмгольца относительно этой функции с заданными начальными условиями. Популярность метода объясняется простотой реализации и достаточной строгостью подхода в приведенных областях оптики.

К сожалению, развитие метода сдерживается его высокой вычислительной сложностью. Так, производители известного пакета OlympIOs [6] вынуждены включить в него модуль для параллельных вычислений. Компания RSoft предлагает различные способы оптимизации параметров и решения под требования заказчика [7]. К настоящему времени известна альтернативная технология снижения длительности расчетов, основанная на векторизации алгоритма. Такие алгоритмы известны достаточно давно [8,9], однако до последнего времени не получили распространения в силу недоступности соответствующей аппаратной базы широкому кругу исследователей. Технология CUDA [10], получившая всеобщее признание с 2007 года, открывает возможность реализации векторных алгоритмов на обычных персональных компьютерах.

С ее появлением вернулся интерес к векторизации хорошо известных численных методов: Гаусса-Зайделя [11], FDTD [12], Ray Tracing [13] и многих других. Для BPM подхода аналогичные исследования в доступной литературе найдены не

были, данной работой авторы рассчитывают заполнить этот пробел.

1. Векторный алгоритм для разностной схемы Кранка-Николсона

Представляя скалярный вариант BPM подхода (двумерный случай), принято [3] рассматривать уравнение Гельмгольца в виде:

d ² U f d ² ,2 2)

TT + I 2 + kо n IU - 0, oz   ^ оy       )

где под величиной U , определенной на вычислительно области D - { ( y,z ): 0 <  y <  L y ;0 <  z <  L_z } , понимают напряженность электрического поля (в случае ТЕ-поляризованного излучения) или напряженность магнитного (в случае TM-поляризованного излучения). Используя приближение «медленно меняющейся огибающей» [2], пренебрегают значением второй производной по z , тем самым понижая порядок дифференцирования. Тогда уравнение (1) представляют как:

dV dz

i I z 2 2

--------I k₀n *

2 k ₀ n * (

k ₀ ² n ²

d

d y ²

V ,

где V ( y, z ) - U ( y, z ) exp( ik ₀ n * z ), k ₀ - волновое число в вакууме, n _* – базовый показатель преломления, характеризующий точность огибающей. При этом распространение излучения в неоднородной среде считают сходным с распространением в однородной среде с показателем преломления n _* . Уравнение (2) называют уравнением Гельмгольца в форме Френеля.

Записывая разностную схему для (2), наложим на D следующую сеточную область:

Dh -

^-u y i , ^z k ^): y i ^- ih y , h y ^- L y ; z k ^- kh z , h z ^- L rl , (3) I                          N                 K I

где h_y и h_z – шаги дискретизации, характеризующие сходимость разностного решения. Тогда схема Кранка-Николсона для уравнения (2) [14] при ис-

следовании распространения излучения в свободном пространстве ( n * = n ₀) примет вид [3]:

У k + 1 _— У ^k h_z

i 6 f У k+1 — 2T k + T k—1J

2 k 0 n * (         h y          ,

;/л        W ^{k +1} 94< ^{k +1} -I- w ^{k +1}

+ i (l-6) T i + 1 ^{— 2 y}    -Л i — ¹

2 k о n * (           hy²           J

где 6 - весовой коэффициент разностной схемы. Введение указанного упрощения не влияет на векторизацию вычислений и преследует исключительно методические цели.

Рассмотрим в качестве начального условия поле T ( у ,0) при z = 0, записав следующую его дискретизацию У ⁰ = T ₀( ih y ). Краевые условия соответствуют расположению идеального проводника на границах D при у = 0 и у = L y : T 0 = У N = 0 .

Приняв весовой коэффициент 6 =0,5 [14], перепишем (4) как:

k+1      k+1                  k+1 _ k-h a (T i+1 + t i —1 ) — (1 + 2 a)T i =— Fi ,              (5)

где р = а (Уk+1 +Tk—1) + (1 — 2a)Tk и a = ihz

4 k ₀ n , h y

Задача свелась к решению системы линейных алгебраических уравнений (СЛАУ) вида Ax = b с ленточной матрицей. Приступая к векторизации вычислений по (5), выберем для решения системы метод однопараметрической итерации [14]. К сожалению, как отмечено в монографиях Дж. Голуба и В. Лоуна [8] и Дж. Ортеги [9], прямые методы решения СЛАУ с узкой лентой эффективно не векторизуются. В выбранном методе приближение к решению x^{s + 1} (на s +1 итерации) равно произведению матрицы P на вектор приближенного решения x^s (на s итерации), сложенный с произведением вектора правой части b на параметр т. При этом P = ( A — т E ), E - единичная матрица, т = 2 / ( % + Л ), % и Л - минимальное и максимальное собственные числа матрицы А соответственно. Такой выбор параметра т обеспечивает оптимальную скорость сходимости [15]. При моделировании среды с меняющимся показателем преломления, возникает необходимость в пересчете собственных чисел матрицы A . Авторы полагают возможным в силу плавности изменения среды производить пересчет не на каждом пространственном слое разностной схемы, а через определенные промежутки. Тогда доля длительности расчета значений % и Л в общем времени вычислений может быть минимизирована.

Рассмотрим следующую схему компактного хранения матрицы по диагоналям. Ранее Дж. Голуб и В. Лоун [8] применяли аналогичный подход для хранения симметричной матрицы.

Пусть матрица А имеет вид (рис. 1):

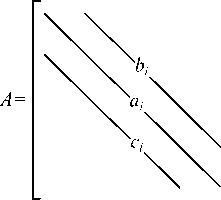
Рис. 1. Ленточная матрица А, где верхняя ширина ленты и нижняя ширина ленты q=p=1, соответственно

1≤ i ≤ N для ai , 1≤ i ≤N-1 для bi и сi

Тогда при хранении по диагоналям представим матрицу А в виде:

^A dag = ^[ a 1 , •"^, a N 1,

B diag = [ Ь 1 , - , b_N — 1 ],                               (6)

^C diag = ^[ c 1 , ""’ c N — 1 ^].

Выбирая более сложный дифференциальный шаблон, можно придти к матрице с большей шириной верхней и нижней ленты, для общности положим ширину верхней и нижней ленты произвольной и равной p и q соответственно. Тогда элемент матрицы A ( i , j ) хранится в одном из векторов A_diag , B_diag и C_diag в соответствии со следующим правилом:

A diag ( i ),    i = j ,

A ( j + h , j ) = C diag (( h — 1) N —

A ( i , j ) =) — h ( h — 1) / 2 + j ), i >  j + h ,

A ^{( i} , ⁱ + m ) = B diag ⁽⁽ m ^— 1) N ^—

— m (m — 1) / 2 + i), i < j — m, где h и m - номера диагоналей в нижней и верхней ленте, для которых справедливо неравенство 1 < h < p и 1 < m < q .

Умножение матрицы на вектор z = Ax (основная операция в методе) может быть записана следующим образом в нотации из [8].

Алгоритм умножения матрицы на вектор:

z = Adiag. * x % умножение главной диагонали на вектор х for m = 1 : q %проход по верхней ленте t = (m — 1)N — m(m —1)/2% номер 1-го элемента поддиагонали в массиве, хранящем верхние ленты z (1: N — m) = z (1: N — m) +

+ B_diag ( t + 1: t + N — m ).* x ( m + 1: N );

end for h = 1 : p %проход по нижней ленте t = (h — 1)N — h (h — 1) / 2 % номер 1-го элемента поддиагонали в массиве, хранящем нижние ленты z (h +1: N) = z (h +1: N) +

+ C diag ( t + 1: t + N — h ). * x (1: N — h );

end

Правило хранения матрицы по диагоналям и векторный алгоритм представлены для ленточных матриц, с произвольной шириной верхней и нижней ленты. Заметим, что во внутренних циклах происходит покомпонентное произведение векторов, обозначенное в алгоритме «.*» (на многих процессорах производится аппаратно), и осуществляется доступ к последовательно расположенным в памяти данным (что значительно ускоряет вычисления).

2. Реализация векторного алгоритма на видеокарте NVIDIA GeForce GTS 250

Результаты, представленные далее, получены на видеокарте GeForce GTS 250.

Таблица 1. Основные характеристики GPU NVIDIA GeForce GTS 250

Характеристика	Значение
Количество мультипроцессоров, шт.	16
Размер видеопамяти, Мб	1024
Максимальное число потоков в блоке, шт.	512
Максимальная размерность блока потоков ( x , y , z ), шт.	512*512*64
Максимальная размерность сетки блоков, шт.	65535 * 65535 * 1
Тактовая частота ядра, МГц	702
Тактовая частота памяти, МГц	1000

Кроме того, использовался процессор Intel Core Duo E7500.

Таблица 2. Основные характеристики CPU Intel Core Duo E7500

Характеристика	Значение
Тактовая частота ядра, ГГц	2,93
Тактовая частота шины CPU, МГц	1066
Кеш L1, Кб	64*2
Кеш L2, Кб	3072
Пропускная способность шины процессор-чипсет, ГБ/с	8,528
Ширина шины L2 кеша, бит	256

В вычислительных экспериментах по определению ускорения моделирование распространения электромагнитного излучения проводилось для полого волновода с идеальными проводящими стенками. В качестве начального условия была взята мода волновода:

Л A

T ( y ,0) = sin

yn п T

V y 7

где L _y – его ширина. Данные условия выбраны для простоты верификации разностного решения. Длина волны принималась равной % = 1 мкм, ширина волновода L _y = 10 мкм, L _z = 100 мкм, показатель преломления среды n = 1.

Число узлов сеточной области N менялось от 100 до 3000. Соответственно h y = L _y I N , h _z = h _y I п (для асимптотической устойчивости [14]).

Исследование велось в операционной системе Microsoft Windows XP, 32-bit (Service Pack 3) с установленным драйвером NVIDIA CUDA 2.3 driver. Скалярный и векторный алгоритмы написаны с использованием программного пакета Microsoft Visual Studio 2008 Express Edition.

Приведем ядро (kernel в терминах [10]) для GPU, выполняющее основную операцию описанного выше векторного алгоритма (умножение матрицы на вектор).

__global__ void matrixMulfVextor( cuFloatComplex* d_Bdiag, cuFloatComplex* d_Cdiag, cuFloatComplex* d_Adiag, cuFloatComplex* d_x0, cuFloatComplex* d_bt, cuFloatComplex* d_x, int N)

//номер элемента в блоке

{int i = blockIdx.x * blockDim.x+threadIdx.x;

//умножение главной диагонали на вектор x и суммирование с вектором правой части.

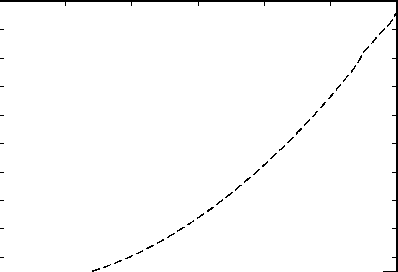
if(i

} __syncthreads();

//умножение верхней ленты на вектор x if(i

} __syncthreads();

d_x[i]=cuCsubf(d_x[i], cuCmulf(d_Cdiag[i-1],d_x0[i-1]));

} __syncthreads();

// переход с k(итерации) на k+1(итерацию)

if(i

}__syncthreads();

На вход в ядро передаются вектора главной диагонали ( Adiag из (6)), верхней и нижней лент ( Bdiag и Cdiag из (6)) и правой части. Размер блока равен 256 потокам (thread в терминах [10]), размер сетки (grid в терминах [10]) выбирался равным N / 256. На каж- дом мультипроцессоре может исполняться совокупность потоков до 24 (24 warp в терминах [10]) или 768 потоков (размер warp = 32 потока). За счет этого и достигается высокая производительность.

В скалярном варианте авторы остановились на итерационном методе решения (5) и для CPU как на методе не только обеспечивающем корректное сравнение эффективности обеих реализаций (векторной и скалярной), но и позволяющем в будущем использовать векторные инструкции SSE центрального процессора.

На рис. 2 виден эффект от применения векторных вычислений.

t, с

О 500   1000 1500 2000 2500 N

Рис. 2. Время выполнения BPM метода (пунктирной линией) на CPU и (сплошной) на GPU

Зависимость времени выполнения от размерности задачи для CPU параболическая, а для GPU - линейная. Это объясняется тем, что с ростом размерности задачи число скалярных операций увеличивается пропорционально квадрату размерности сеточной области, а число векторных операций растет линейно. Существенной разницы на участке размерности от 100 до 400 узлов сетки нет, что связано с возможностью центрального процессора быстро обрабатывать небольшое количество данных, которое может быть помещено в его кеш (cache). С ростом размерности задачи такая возможность исчезает и тысячи процессорных тактов уходят на пересылку данных из оперативной памяти в кеш и обратно. Кроме того, центральный процессор выполняет ряд системных инструкций, снижающих производительность. Длительность выполнения вычислений для одного шага по z на GPU в 22,5 раз меньше аналогичной операции для CPU для размерности исходной матрицы N * N = 3000 * 3000. Проведенные исследования для значений n > 15000 показали появление параболической зависимости длительности вычислений от размерности задачи и для векторного алгоритма, что связано с ограниченным размером памяти видеокарты. Однако среди реализаций BPM, встреченных авторами в литературе, отсутствуют сеточные области с упомянутой размерностью. Следует отметить, что, хотя векторное ускорение, получаемое при выполнении кода на видеокарте, велико, это вполне ожидаемый результат, учитывая особенности архитектуры GPU. В отличие от CPU, где большая часть ядра отдана под кеш и сложные арифметикологические устройства (АЛУ), на графическом ядре размещено большое количество упрощенных АЛУ, которые имеют общую память на кристалле.

Заключение

В настоящей работе создан векторный алгоритм для решения уравнений разностной схемы Кранка-Николсона. Данный алгоритм реализован с использованием технологии CUDA применительно к BPM-FD методу. Сравнение векторного алгоритма, выполняемого на GPU, cо скалярным аналогом на CPU продемонстрировало увеличение производительности в 22,5 раза для размерности задачи 3000 * 3000. Таким образом, представляется перспективным использование технологии CUDA для вычислений и по другим BPM методам.

Работа выполнена при поддержке грантов РФФИ № 10-07-00553-а, 10-07-00453-а и 10-01-00723-а и гранта Президента РФ №НШ-7414.2010.9.