Векторная частица с аномальным магнитным моментом во внешнем однородном электрическом поле

В настоящей работе будут найдены точные решения уравнения Даффина-Кеммера для частицы со спином 1 и дополнительной электромагнитной характеристикой — аномальным магнитным моментом [1–7]. Используется де-картовая сиcтема координат. Для 10-компонентного поля вводятся три проективных оператора [8], которые позволяют разложить волновую функцию в сумму трех частей. Од- на из составляющих, зависящая от четырех функций, является основной, две другие могут быть выражены через нее. Для этих четырех функций выведено линейное условие связи, в результате возникает система из трех связанных дифференциальных уравнений 2-го порядка для трех функций. Эта система после специального линейного преобразования приводится к трем несвязанным уравнениям для трех новых функций. Их решения построены в терминах вырожденных гипергеометрических функций.

1.    Обобщенное уравнение Даффина-Кеммера, разделение переменных

Исходим из общего уравнения для частицы со спином 1 и аномальным магнитным моментом

{ в c ( d c - ieA c ) + A 2 F ab ( x ) J ^ab P - M }» = 0 ,

P = (1 4 oA

P ^0 o),

где P — проективный оператор, выделяющий векторную компоненту из волновой функции. В однородном электрическом поле A t = -Ez, F tz = F 03 = E уравнение записывается в виде

[ в ° ( ^d + iEz ) + в 1 ^d + в 2 1" +

∂z           ∂x ∂y

+в3d +ГJ03P - M]Ф = 0, (2) ∂z где размерности величин такие:

[ M ] = 1 /L, r = iAE, I, [Г] = 1 /L, [ E ] = 1 /L ² , [ t ] = 1 /L ;

величина Г — чисто мнимая. Для волновой функции используем подстановку

-iϵt iax iby ^H 1

* e e e   ^Я 2^ ’

Я 1 = ( h ° ( z ) ,h 1 ( z ) ,h 2 ( z ) ,h з ( z )) t ,

Я 2 = ( E i ( z ) ,E 2 ( z ) ,E з ( z ) ,B i ( z ) ,B 2 ( z ) ,B з ( z )) t , где t обозначает транспонирование. Соответственно, уравнение принимает вид

[ i ( Ez - € ) в ° + iaв 1 + ibв 2 +

+ в ³ dd +r j ⁰³ p - m ]ф( z ) = o . (3)

При использовании блочной формы a 0   La p   ^Ka  0 )

имеем два уравнения

[i ( Ez - € ) L ° + iaL ¹ + ibL 2 +

+ L ³ d ] Я 2 + Г j °³ Я i - MH i = 0 , (4) dz

[i ( Ez - € ) K ° + iaK ¹ + ibK 2 +

+ K ³ d ] Я 1 - MH 2 = 0 . (5) dz

Приводим явный вид всех матриц в декартовом базисе

	0		0		0	0		0	0
L 0	= ^	- 1 0		0 - 1	0 0	0 0		0 0	0 0
		0		0	-	10		0	0
		- 1		0	0	0	0		0 \
L 1	= 1	0 0		0 0	0 0	0 0	0 0		0 1 1
		0		0	0	0	- 1		0
		0	-	1	0	0	0	0
L 2	= 1	0 0		0 0	0 0	0 0	0 0	-	1 0
		0		0	0	1	0	0
		0	0		1	0	0		0
L 3	= ^	0 0	0 0	0 0	1	0 - 1	+1 0		0 0
		0	0	0		0	0		0
				( 0	1	0	0^
				0	0	1	0
	K	° =		0	0	0	1
				0	0	0	0	,
				0	0	0	0
				0	0	0	0
			Л	- 1	0	0	0	\
				0	0	0	0
	K 1			0	0	0	0
				0	0	0	0		,
				0	0	0	- 1
				0	0	1	0
			(	0	0	0		\
			•	- 1	0	0	0
	K 2			0	0	0	0
				0	0	0	1		,
				0	0	0	0
			0		- 1	0		V
		/		0	0	0	0 \
				0	0	0	0
	K 3			1	0	0	0
				0	0	- 1	0		,
				0	1	0	0
			0		0	0	0
				0	0	0	1\
	03			0	0	0	0
	j 1	=		0	0	0	0	,
				1	0	0	0
		( 0		0	0	0	1		0 \
		0		0	0	- 1	0		0
03		0		0	0	0	0		0
j 2	=	0		- 1	0	0	0		0
		1		0	0	0	0		0
		0		0	0	0	0		0

После простых вычислений получаем систему уравнений по переменной z

-iaE 1 - ibE 2 + Г h 3 - E 3 = mh 0 ,

-ibB з — i (Ez - €) E i + B 2 = Mh 1, iaBз - i (Ez - €) E2 - B1 = Mh2, ibB 1 - iaB2 - i (Ez - €) E3 + Гh0 = Mh3,

-iah 0 + i ( Ez - € ) h 1 = ME 1 ,

-ibh0 + i (Ez - €) h2 = ME2, i (Ez - €) h3 - h0‘ = ME3, ibh3 - h2 = MB 1,

-iah 3 + h' 1 = MB 2 ,

-ibh1 + iah2 = MB3, где штрих обозначает производную по z.

2.    Проективные операторы, метод Федорова-Гронского

Ниже будем использовать метод Федорова-Гронского [8]. Пусть

_Y _ (j 1⁰³    0 \

Y          J 03) •

Убеждаемся, что выполняется минимальное уравнение

Y ( Y - 1)( Y + 1) = 0 . Это уравнение позволяет ввести три проективных оператора

П 1 = 2 Y ( Y + 1) , П = 2 Y ( Y - 1) ,

П 3 = 1 - Y ² •                  (7)

С учетом их явного вида получаем выражения для трех проективных составляющих

Ф 1 = ЩФ =

= ⁽ h 0 , 2 ^h 1 , 2 ^h 2 ^,h 3 ^,E 1 ^,E 2 , 2 ^E 3 ^,B 1 ^,B 2 ’ 2 ^B 3 ) t ,

Ф ₂ = П ₂ ф =

= ⁽⁰ ,^- 2 ^h 1 ,^- 2 ^h 2 , ⁰ , ⁰ , ⁰ ,^- 2 ^E 3 ’ ⁰ ’ ⁰ ’^- 2 ^B 3 ) t ,

Ф 3 = П 3 Ф = (0 , h 1 ,h 2 , 0 , 0 , 0 , E 3 , 0 , 0 , B 3 ) t .

Будем рассматривать переменную Ф ₃ как основную, она зависит от функций h 1 , h 2 , E 3 , B 3 . Сначала шесть уравнений из системы (6) решаем как алгебраические относительно неосновных переменных h 0 ,h 3 ,E 1 ,E 2 ,B 1 ,B 2 , этодает

• ^{h 0} = ^- ( a 2 + b 2 + M 2 ) 2 - Г 2 m 2 [ ^{-ah 1 (} a 2 ^{+ b} 2 ^{+ M 2} ) •

• ■ ( Ez - € ) - a ² bEzh 2 + a ² b€h 2 + a ² ME ‘3 + ia Г Mh 1 + + b ³ ( -E ) zh 2 + b ³ €h 2 + b ² ME 3 -bM ² Ezh 2 + bM ² €h 2 +

+ibГMh2 + M3E3 + iГM2 E3(Ez - €)], h3     (a2 + b2 + M2)2 - Г2M2 [i(a3h1 + ME3X x (a2 + b2 + M 2)( Ez-€)+ b (a2 + b2 + M 2) h2 + ab2 h'1 + +aM2h'1 + iaГMh 1(Ez - €) + ibГMEzh2 -

-ib Г M€h ₂ - i Г M ² E ₃ )] ,

E ¹ = - M ( a ² + b ² + M 2 ) 2 - Г ² M ³ [ i ⁽ a ⁽ bh ^{2 X} x ( a ² + b ² + M ² )( Ez - € ) - M (( a ² + b ² + M ² ) E 3 + + i Г( ah ‘ 1 + bh ₂ ))) -h 1 ( Ez-€ )(( b ² + M ² )( a ² + b ² + M ² ) -- Г ² M ² ) - ia Г M ² E ₃ ( Ez - € ))] ,

E ² = - M ( a ² + b ² + M 2 ) 2 - Г ² M ³ [ i ⁽ a 4 Ezh ² --a ⁴ €h ₂ - abh 1 ( a ² + b ² + M ² )( Ez - € )+ + a ² b ² Ezh ₂ - a ² b ² €h ₂ + a ² bME 3 + +2 a ² M ² Ezh ₂ - 2 a ² M ² €h ₂ + iab Г Mh ‘ 1 +

+ b ³ ME 3 + b ² M ² Ezh ₂ - b ² M ² €h ₂ + ib ² Г Mh 2 + + bM ³ E 3 + ib Г M ² E 3 ( Ez - € ) + M ⁴ Ezh 2 -

-M ⁴ €h 2 - Г ² M ² Ezh 2 + Г ² M ² €h 2 )] ,

B1 = M(a2 + b2 + M2)2 - Г2M3 [bM((Ez - €)X x (E 3 (a2 + b2 + M 2) + i Г( ah 1 + bh 2)) - i Г ME 3) --ah2((a2 + M2)(a2 + b2 + M2) - Г2M2) +

+ ab ( a ² + b ² + M ² ) h 1 ^] ,

B ² = M ( a ² + b ² + M 2 ) 2 - Г ² M ^{3 [} -aME ^{3 X}

x ( a ² + b ² + M ² )( Ez - € ) - ab ( a ² + b ² + M ² ) h 2 + + a ² b ² h ‘ 1 + a ² M ² h ‘ 1 - ia ² Г Mh 1 ( Ez - € ) --iab Г MEzh ₂ + iab Г M^h ₂ + ia Г M ² E ‘3 + + b ⁴ h ‘1 + 2 b ² M ² h' 1 + M ⁴ h ‘1 - Г ² M ² h ‘1 ^] .

Полученные выражения подставляем в оставшиеся четыре уравнения; в результате находим уравнения для основных функций h 1 , h 2 , E 3 , B 3 . Будем использовать новые переменные

G = ah 1 + bh2, H = bh 1 - ah2,(8)

тогда уравнения для функций G, H, E ₃ , B ₃ запишутся так:

a(a ² E + b ² E + M(ME - i Г( € - Ez )²))

• 1)           (a2 + b2 + M2)2 - Г2M2

ia Г M,,

+ (a2 + b2 + M2)2 - Г2M2 3 + aM(a2 + b2 - Г2 + M2) + (a2 + b2)((a2 + b2 + M2)2 - Г2M2)

b _′′

+ ( a ² + b ² ) M

bM ² - ( e - Ez )²) M ( a ² + b 2 )

( a ² + b 2 ) (( a ² + b ² + M 2 ) 2 - Г ² M 2) a a 4 M ⁺

+ a 2 (2 b ² M + 2 M ³ - M ( e - Ez ) ² + i Г E ) + b ⁴ M +

+ b 2 (2 M ³ -M ( e-Ez ) ² + i Г E )+ M ( M - Г)(Г+ M ) x x (M ² - ( e - Ez )²)] G - ibB 3 = 0 , b(a ² E + b ² E + M(ME - i Г( e - Ez )²))

• 2)           (a2 + b2 + M2)2 - Г2M2

ia Г M,,

+ (a2 + b2 + M2)2 - Г2M2 3 + bM(a2 + b2 - Г2 + M2)

⁺ ( a ² + b ² )(( a ² + b ² + M ² ) ² - Г ² M ² )

- ^a    н " ₊ ^{a ( M 2 - ( e -} Ez ^{) 2 )} H-

M ( a ² + b ²           M ( a ² + b ² )

• - ( a ² + b ² ) (( a ² + b ² + M ² ) ² - Г ² M ²) b [ a 4 M ⁺

+ a ² (2 b ² M + 2 M ³ - M ( e - Ez ) ² + i Г E ) + b ⁴ M +

+b2 (2 M 3-M (e-Ez )2 + i Г E) + M (M - Г)(Г+M) x x (M2 - (e - Ez)2)] G + iaB3 = 0,

M ( a ² + b ² + M ² )

• ³⁾    ( a ² + b ² + M ² ) ² - Г ² M ^{2 3 +}

⁺ ( a 2 + b 2 + M M 2 ) 2 - Г 2 M 2 M [ -a 4 ⁺ a ^{2 (} - ² b ² -

- 2 M ² + ( e - Ez ) ² ) - b ⁴ + b ² (( e - Ez ) ² - 2 M ² ) + + M --M ³ + M (Г ² + ( e - Ez )²) + i Г E )^] E ₃ +

₊       i Г M      G

( a ² + b ² + M ² ) ² - Г ² M ²

(a ² E + b ² E + M^ME - i Г( e - Ez )²))^ ( a ² + b ² + M ² ) ² - Г ² M ²       G = ⁰ ’

• 4)    - MB ₃ - iH = 0 ^ B ₃ = -Mi^H.

Складываем и вычитаем уравнения 1) и 2), в результате получаем i Г M (a + b)

( a ² + b ² + M ² ) - Г ² M ^{2 3}

• ⁺ ( a 2 + b 2 )(( a 2 + b L M 2 ) - Г 2 M 2 )⁽ a ⁺ b ^{) [} a 4 ⁽ -M ^{) +}

+ a ² ( - 2 b ² M - 2 M ³ + M ( e - Ez ) ² - i Г E) - b ⁴ M +

+ b ² ( - 2 M ³ + M ( e - Ez ) ² - i Г E) - M ( M ² - Г ² ) x x ( M + Ez - e )( M - Ez + e )] G + i ( a - b ) B 3 = 0;

i Г M ( a - b )

( a ² + b ² + M ² ) ² - Г ² M ^{2 3}

(a - b) (a2E + b2E + M(ME - iГ(e - Ez)2)),

(a2 + b2 + M2)2 - Г2M2

,   (a + b)   H‘‘ - (a + b)(M2 - (e - Ez)2) H+ a2 M + b2 M           M (a2 + b2)

+  M(a - b)(a2 + b2 - Г2 + M2)

( a ² + b ² ) (( a ² + b ² + M ² ) ² - Г ² M ²)

⁺ ( a 2 + b 2 ) ⁽ ( a 2 + b L M 2 ) - Г 2 M 2 )⁽ a ⁺ b ^{) [} a 4 ⁽ -M ^{) +}

+ a ² ( - 2 b ² M - 2 M ³ + M ( e - Ez ) ² - i Г E) - b ⁴ M +

+ b ² ( - 2 M ³ + M ( e - Ez ) ² - i Г E) - M ( M ² - Г ² ) x x ( M + Ez - e )( M - Ez + e ) ^] G - i ( a + b ) B 3 = 0 .

Данные уравнения можно записать в более короткой форме, если использовать обозначения

K = iTM, a2E + b2E + M^ME - iГ(e - Ez)2)

L =                D              ,

N = -     ¹ P = ^{M 2} - ( e - Ez ) 2

M ( a ² + b ² ) ’          M ( a ² + b ² ) ’

_ M ( a ² + b ² - Г ² + M ² )

=       ( a ² + b ² ) D      ’

T =         [ -Ma ⁴ + a ² ( - 2 b ² M - 2 M ³ +

( a ² + b ² ) D

+ M ( e-Ez ) ² -i Г E)-b ⁴ M + b ² ( - 2 M ³ + M ( e-Ez ) ² --i Г E)-M ( M ² - Г ² ) ( M ² - ( e - Ez )²)^] ,

D = ( a ² + b ² + M ² ) - Г ² M ² .

Тогда они примут вид

⁽ a ⁺ b ) Kdz 2

-

l 1 E 3 + ( a - b ) N-d ²- + p\ H + dz ²

-

( a + b )( a ² E + b ² E + M(ME - i Г( e - Ez )²))   ,

( a ² + b ² + M ² ) ² - Г ² M ²          E 3 ⁺

+ ( a + b ) O d 2 + T G + i ( a - b ) B 3 — 0 ,

⁽ b ^- a )         ⁽ a ^- b ) ( M ^{2 - ( e -} Ez ⁾²)

⁺ M ( a ² + b ² )   ⁺       M ( a ² + b ² )        ⁺

( a - b )

d ²

^Kdz ²

-L

E ₃ - ( a + b )

N^d ² + p I h + dz ²

M ( a + b )( a ² + b ² - Г ² + M ² )

⁺ ( a ² + b ² )(( a ² + b ² + M ² ) ² - Г ² M ²)   ⁺

+( a - b )

Oz ⁺ T

G - i ( a + b ) B ₃ — 0 .

В (9) первое уравнение разделим на ( a + b ) , а второе — на ⁽ a - b )

+

i Г M

( a ² + b ² + M ² ) ² — Г ² M^{1 2}

_G ′′

-

[

_K d ² dz ²

- Ae 3 + a-b Nd + p"\h +

J a + b dz ² J

+

o^ + T dz ²

K ^{d 2} - L E dz ²

-

+

G + i

a-b a + b

a + b a-b

O-^ + T G dz ²

-

и вычтем результаты, получим

a-b

\ a + b

+

a + b a-b

B 3 = 0 ,

[ N   + p]h+ dz2

a + b

i

a

-

b

B 3 = 0

^NT 2 + p I h + iB 3?

dz ²

0 •

(a2 E + b2 E + M^ME — i Г( e — Ez )2))^

(a2 + b2 + M2)2 — Г2 M2      G = 0, его можно записать так:

(O' AA + T ') E 3 + К2— — L}G =0,(16)

dz2

где учитываем прежние и добавленные обозначения

O ' = D M ( a ² + b ² + M ² ) ,

T ' = D [ —Ma ⁴ — 2 Ma ² b ² — 2 M ³ a ² + Ma ² ( e — Ez ) ² —

—Mb ⁴ + Mb ² ( e — Ez ) ² — 2 M ³ b ² — M 5 +

+ M ³ Г ² + M ³ ( e — Ez ) ² + iM ² Г e] •

Откуда следует

[ N^ 2 + p I h + iB з = 0 . dz ²

Из (11), учитывая четвертое уравнение iB 3 = Hr находим уравнение для функции H:

Выпишем уравнения для функций E ₃ , G (пусть E ₃ = F ):

d ²

1 ■

Ndz ^{2 +} P ⁺ MH ⁰ •

(Кт2 — l}f + Oo^AA + t)g = 0 , dz ²                dz ²

f o' d^ + T'

dz ²

_K d ² dz ²

-

L]G = 0 .   (17)

Умножаем первое уравнение в (17) на некоторый параметр α , второе — на параметр β и результаты складываем. Есть две возможности.

Первая возможность:

Теперь первое уравнение в (9) разделим на ( a — b ) , а второе — на ( a + b )

a + b к d ²

a - b   dz ²

-

L

E 3 +

d ²

N-^ + P H + dz ²

aK + eO = 1 , а0 + вК = 0 ^

^ d L F + ( —aL + eT ' ) F + ( aT — вА ) G = 0 ,

при этом

+ a+b Adr^ + t]g + iB 3 = 0 ’ a - b dz ²

a — b к d12

a + b   dz ²

-

L

E 3 ^-

N^² + p I h +

+ a-b O⁰^ + Ag — iB 3 = 0 • a + b dz ² J

Складывая два последних уравнения, получаем

[ К"^ — a ] E 3 + [ 0^4 + T ] G = 0 • dz ²                dz ²

Осталось неиспользованным третье уравнение

_ К _ i Г( a ² + b ² )

^a = к ² — oo ' = M ’

O _a ² + b ² — Г ² + M ²

в = — К2 — OO' = M и уравнение 2-го порядка принимает вид d—F + (—a2 — b2 + Г2 — M 2 + dz2

⁺ iM ^{+ W 2} ) F ⁺( —M ⁺ i ^Г) G =0 .

Вторая возможность:

aK + eO = 0 , aO + вК = 1 ^

+

M (a ² + b ² + m ² )

( a ² + b ² + M ² ) ² — Г ² M ^{2 3 +}

^ ( —aL + eT ' ) F + ^d-- G + ( aT — вА ) G = 0 , dz ²

( a ² + b ² + M ² ) ²

— Г ² M ²

M [—a ⁴ + a ² ( — 2 b ² —

при этом

— 2 M ² + ( e — Ez ) ² ) — b ⁴ + b ² (( e — Ez ) ² — 2 M ² ) + + M—-M ³ + M (Г ² + ( e — Ez )²) + i Г E )^] E 3 +

O ^′

OO ^′ - K ²

( a ² + b ² )( a ² + b ² + M ² ) M

К         i Г( a ² + b ² )

OO ' — К ² = M

и уравнение 2-го порядка примет вид

( ( a ² + b ² )( E - i Г M A      dd

I M F^{F +} dz 2 G ⁺

+( -a ² - b ² - M ² + W 2 )G = 0 .      (21)

is 11 = A 1 s 12 ,

s 11 = -i ^ S 12 =   ;

λ 1

a 2 = 2 (r+Vr ² - 4 pp ²

После необходимых вычислений находим явный вид уравнений (19) и (21):

( d^ + W ² - a ² - b ² - M 2^ F = dz ²

=- r(r+M)F - i(r+M) G f dk + W2 - a2 - b2 - M 2) G = dz2

= -i ( a ² + b ² )^r+ ME^F.          (22)

Введем обозначения

A = (4+ + W ² - a ² - b ² - M ²) , dz ²

a2 + b2 = p2, Г+ M = CT = iAE + ME, тогда система принимает вид

AF = -стГF - гстО,  AG = -Ap2F, или

^A У =            A = G p 2 o) . ⁽²³⁾

Найдем преобразование, диагонализирующее матрицу смешивания A :

is ₂₁ = A ₂ s ₂₂ ,

s 21 = ^-i ^ s 22 = . . λ 2

Таким образом, матрица преобразования S задается соот-

ношениями

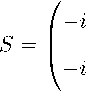
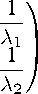
AФ = -cta Ф , Ф ‘ = S Ф , S ^{— 1} A = Ф ^

AФ ‘ = -ctSAS ^— 1 Ф ‘ ,

Ф ‘

т. е. получаем уравнение

SAS ^{- 1} = A = P, ^{1 0} ) ^ \ o A 2 у

⇒

s 12

^s 22

s 11

s 21

s 12

^s 22    ^,

или

⁽ Г -_i A 1

ip ) ( s ¹¹ ) = 0

^-λ 1     ^s 12

(^r -i^{A 2}

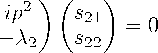
С учетом уравнения для диагональных элементов - Г A + A ² + p ² = 0 находим следующее решение:

A 1 = Vr - V P ² - 4 p ² ) = i p E - V A ² E ² + 4 p ² ) , ² \               / ² \                    /

/    iA 1

'— 1 = I A 1 - A 2 λ ₁ λ ₂

-

λ 1 - λ 2

iλ 2

λ 1 - λ 2 λ ₁ λ ₂

λ 1 - λ 2

После выполненного преобразования имеем два раздельных уравнения:

(A + ctA 1) F = 0, (A + ctA 2) G = 0, d2

A = —- + W ² - p ² - M ² .       (26)

dz ²

Их решения будут приведены в следующем разделе.

3. Построение решений основного уравнения

Уравнения (26) имеют ту же структуру, что и в случае обычной скалярной частицы во внешнем электрическом

поле ₂

(d . + ( Ez + e ) ² - p ²) Ф( z ) = 0 .     (27)

dz ²

Преобразуем уравнение (27) к новой переменной (предполагаем, что E >  0 ): Z = i ( Ez + e ) ² /E, ct = p ² / 4 E , в результате получаем

d ²

( dZ 2 ⁺

1 / 2 d

Z dZ

-

4 + i-CT-A ф( z ) = 0 .

Это уравнение с двумя особыми точками. Точка Z = 0 регулярная, поведение решений около нее задается формулами Z ^ 0 , Ф( Z ) = Z A , A = 0 , 2 . Точка Z = \ нерегулярная, ее ранг равен 2 . Действительно, переходя к обратной переменной y = Z ^— 1 , получим

/ d2    3 / 2 d dy2    y dy

-

Л+ CT) ф=0 . ⁴ y ⁴ y ³ /

Асимптотическое поведение при у ^ 0 должно иметь структуру Ф = y ^C e ^D/y , откуда следует

D 1 = 2 , C 1 = 4 ⁺ i^CT ;

D 2 = ^- 2 , C 2 = 4 ^{- iCT}.

На бесконечности возможны два типа асимптотик:

Z ^^, ф = z ^—C e ^DZ =

J Z -C 1 e D 1 Z = Z - ¹ / 4 -i, e Z//2

I Z -C 2 e D 2 Z = Z - 1 / 4+ i, e -Z/²

где (используем главную ветвь логарифмической функции)

₇ ■ ( e + Ez ) ²

^Z = i---6 ---= ^iZ 0 ,

E

заключаем, что решение для Ф 1 ( Z ) задается вещественной функцией, а второе решение Ф ₂ ( Z ) обладает простой симметрией относительно комплексного сопряжения:

Ф 1 ( Z ) = [Ф 1 ( Z )] * , Ф 2 ( Z ) = i [Ф 2 ( Z )] * . (38)

Z о >  0 , e ±^{z/ 2} = e ±^iZ о / ² ,

_Z - 1 / 4 ∓iσ

= ( e lniZ о ) - 1 / 4 ^ia = eg ln Z o + in/ 2^

- 1 / 4 ∓iσ

Найдем решения во всей области изменения переменной Z . Для этого применим подстановку Ф( Z ) = Z A e BZ f (Z ) , что приводит к

[ ZdZ ⁺(² A ⁺2⁺² B^Z ) dZ ⁺ df ⁽ Z ⁾=⁰ -

Учитывая ограничения A = 0 , 1 / 2 , B = — 1 / 2 , упрощаем уравнение до следующего:

d ²

ZdZ ^{2 +}

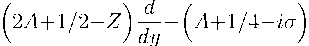
= 0 ,

Данное уравнение вырожденного гипергеометрического типа с параметрами a = A +io, c = 2 A +—, 42

f (Z) = ZAe-Z/2F(a, c; Z).(32)

Без потери общности полагаем

A = 0, a =io, c = -, ’            4         ,2

Ф( Z) = e-z/2 f (Z).(33)

Уравнение вырожденного гипергеометрического типа имеет разные наборы линейно независимых решений. Сначала рассмотрим следующую пару:

Y1 (Z) = F(a, c; Z) = ezF(c — a, c; —Z),(34)

Y 2 ( Z ) = Z ^{1 -c} F ( a — c + 1 , 2 — c ; Z ) =

= Z1 -cezF(1 — a, 2 — c; —Z).(35)

Это приводит к полным решениям в виде

Ф 1 = e ^{-z/ 2} F ( a, c ; Z ) = e ^{z/ 2} F ( c — a, c ; —Z ) , (36)

Ф ₂ = e ^{-Z/ 2} Z ^{1 -c} F ( a — c + 1 , 2 — c ; Z ) =

= Z1 -ce+z/2F(1 — a, 2 — c; —Z).(37)

Учитывая тождества

11 c =2, a = 4 — io, c — a = 4 + io = a , c = c =2, Z = —Z, a — c +1 = 4 — - = (1 — a)*, (2 — c) = (2 — c)* = |,

Это свойство можно представить иначе, если воспользоваться другой нормировкой:

1 —i

Ф 2 ( Z ) = ^ Г Ф 2 ( Z ) =

= 1—^фФ2( Z)) = (Ф 2( Z)) *.(39)

При малых Z решения ведут себя так:

Y 1 ( Z ) » 1 ,  Y 2 ( Z ) »VZ =

= ViZo = А/-^(6 + eEz);

eE

Ф 1 ( z ) » 1 ,  Ф 2 ( z ) «Vz =

= ViZo = А1—6 (6 + eEz).(41)

eE

При больших Z = iZ 0 , Z 0 ^ + ^ имеем следующую асимптотическую формулу:

F ( a,c,Z )= (бр^Ц ( —Z ) ^-a + ... ) +

V^{r( c — a} )             /

+ ("Щ e ^z Z ^a-c + ... \ ^{r( a} )

Учитывая тождества

( —z )

-a

.

= ( —iZ 0 ) ^{- 1} / 4+^ia = ( e ln ^{z 0 -in/ 2} ) ¹ / 4+i^a

= e - ( - 1 / 4+ i, ) in/ 2 e ( - 1 / 4+ i, ) In Z о

r( c ) =    Г(1 / 2) Г( c ) =    Г(1 / 2)

Г(c — a)   Г(1 /4 + io), Г(a)   Г(1 /4 — io), получаем

Y1 = F(a-c-Z > = «“ 0 / 2{ Г^^^ X x e-(-1 / 4+ia)in/2 e(-1 / 4+ia)ln z о e-:iZ о / 2 +    (4

,    Г(1 / 2)      ( - 1 / 4 -iσ ) iπ/ 2 ( - 1 / 4 -iσ ) ln Z 0 + iZ 0 / 2

⁺ Г(1 / 4 — io ) e            e

Отсюда, после перехода к полной функции Ф 1 ( Z ) , полу-

чим ф.^ = (г^ ■

■ e ^{- ( - 1} / 4+ ^ia ) ^{in/ 2} e ^{( - 1} / 4+ ^ia )^{ln z} о e ^- '^{, z} о / ² +     (44)

₊     Г(1 / 2)     +( - 1 / 4 -iσ ) iπ/ 2 ( - 1 / 4 -iσ ) ln Z 0 + iZ 0 / 2

⁺ Г(1 / 4 — io ) e             e            e Г

Известия Коми научного центра УрО РАН, серия «Физико-математические науки» № 5 (57), 2022

В (44) можно увидеть два сопряженных друг другу слагаемых. Аналогично исследуется поведение и второго решения

Y 7 _

£(1___ c ) Y _{1 -} r^ c 1) _e ^inc Y 2

Г(1 - a )     Г( c - a )

F ( a - c +1 , 2 - c,Z ) _ '² c ( -Z ) ^{-a +} c^{- 1} + ^{r(1 -} a )

-1—Л2— c L _e Z z a^{- 1}

Г( a - c + 1)

.

С учетом этого легко находим поведение функций при

\Z| ^ ^

Y 5 _ Ф( a,c ; Z ) _ Z ^-a _

Отсюда, с учетом равенств

( -Z ) ^{-a + c- 1} =

= ( _- iZ o ) ^{- 3} / 4+ ^ia _ ( e ^{ln Z} 0 ^{-in/ 2} ) ^{- 3} / 4+ ^ia _ _ e- ^{( -} 3 / 4+ i^a ) i^{n/ 2} e ^{( -} 3 / 4+ i^a ) ln Z 0

Z a- 1    ( iZ o ) - 3 / 4 -ia   ( e In Z 0 + in/ 2 ) - 3 / 4 -ia _ _e ( - 3 / 4 -ia ) in/ 2 e ( - 3 / 4 -ia ) In Z 0

_ ( iZ 0 ) ^{- 1} / ^{4+ ia} _ ( e ^{ln Z 0 + in/ 2} ) ¹ / 4+ i^a

Y 7 ( Z ) _ e ^Z Ф( c - a, c ; -Z ) _ e ^Z ( -iZ o ) ^a-c _

_ e ^{iZ 0} ( -iZ 0 ) ^{- 1} / ^{4 -ia} _

Г(2 - c )

Г(3 / 2)

Г(1 - a )   Г(3 / 4 + iff ) ’

_ e iZ 0 ( e ln Z 0 -in.

- 1 / 4 -iσ

Г(2 - c )

Г(3 / 2)

или

Г(a - c +1)   Г(3/4 - iff) ’ получаем следующее поведение на бесконечности F(a - c + 1, 2 - c, Z) _ eiZ0/2 {   Г(3/2) x

⁽            ’       ’ )            (Г(3 / 4 + iff )

_{x e} - ( - 3 / 4+ ia ) in/ 2 e ( - 3 / 4+ ia ) In Z 0 e -iZ 0 / 2 +

^г(3 / ²⁾     ( — з / 4 _i_a ) in//2

⁺ Г(3 / 4 - iff ) e             ^x

Ф 5 _ e ^{-Z/ 2} Y 5 _

- 1 / 4+ iσ

_ e -^Z 0 / ² I e ^{ln Z} 0 + ^{in/ 2} j

Ф ₇ _ e ^{-Z/ 2} Y ₇ ( Z ) _

_{х е} ( - 3 / 4 -ia ) ln Z о e + iZ о / 2 I .

_ e + iZ 0 / 2 ( _e ln Z 0 -in

- 1 / 4 -iσ

.

Соотвественно, для функции Ф ₂ ( Z ) находим выражение (учтем, что VZ = e ⁽¹ / ^2)(ln Z о + ^{in/ 2} )

Эти функции комплексно сопряжены друг другу.

Ф 2 ( Z ) = V ZZ ¹ / ² F ( a- _ e in/ . ;    r(3 / 2)

( Г(3 / 4 + iff )

- c + 1 , 2 - c, Z ) _

e ^-(^{- 3} / 4+ ^ia)^{in/ 2} x

_{x e} ( - 1 / 4+ ia ) ln Z 0 _e -iZ 0 / 2 +

^г(3 / ²⁾      ( - 3 / 4 _i_a ) in/.,

⁺ Г(3 / 4 - iff ) e             ^x

_x e ( — ¹ / 4 -ia ) ln Z 0 _e + iZ 0 / 2 I, .

Можно построить два решения, которые на бесконечности будут вести себя как комплексно сопряженные функции. Для этого нужно использовать другую пару решений гипергеометрического уравнения:

Y ₅ ( Z ) _ Ф( a, c ; Z ) , Y 7 ( Z ) _ e ^Z Ф( c - a, c ; -Z ) .

Две пары {Y 5 , Y 7 } и {Y 1 , Y 2 } связаны преобразованиями Кеммера

Y 5 _rT1^n Y 1 + ^ГТ ^- Т Y 2 , Г( a — c + 1)       Г( a )

Заключение

Решенная задача допускает обобщение по нескольким направлениям. Так, можно построить решения с цилиндрической симметрией. При этом возникает система из 10 уравнений в частных производных. Зависимость 10 функций от полярной координаты r может быть зафиксирована с использованием проективных операторов, строящихся на основе генератора j ¹² , после чего система из 10 уравнений по координате z решается с применением метода, использованного в настоящей работе. Можно аналогичным способом исследовать уравнение для такой частицы в присутствии внешнего однородного электрического поля, а также учесть два внешних поля одновременно. Наконец, похожий метод исследования применим и в ситуации, когда учитываются две дополнительные характеристики — аномальный магнитный момент и квадрупольный электрический момент. По существу, во всех этих ситуациях срабатывает один и тот же метод Федорова-Гронского, впервые примененный в работе 1960 г. [8]. Можно добавить, что такой подход с использованием проективных операторов применим и в теориях частиц с более высокими значениями спинов, в частности со спинами 3/2 и 2.