Векторное полиномиальное представление законов наведения и анимация движения спутника землеобзора

В статье приводятся краткие сведения о разработанных методах оптимизации законов углового наведения спутника землеобзора для произвольного маршрута сканирующей съемки и методах анализа вектора скорости движения изображения (СДИ) в произвольной точке матриц оптико-электронных преобразователей (ОЭП). Эти методы используют теоретические основы космической геодезии [1-7] и конкретизированы для трассовых, геодезических и криволинейных маршрутов [8]. Приводится технология аналитического представления законов углового наведения спутника при сканирующей съемке, основанная на интерполяции расчетных данных векторной функцией модифицированных параметров Родри-га, а также результаты, которые демонстрируют эффективность разработанных алгоритмов.

При проектировании космических систем наблюдения, в том числе с применением сканирующей съемки поверхности Земли, применяются компьютерные средства 3D-анимации. Решение общей задачи моделирования, имитации и анимации движения космического аппарата (КА) представляется следующими этапами: расчет параметров поступательного орбитального и углового движения КА для заданной последовательности различных маршрутов съемки; визуализация поверхности Земли с учетом освещённости; расчет трассы полета, зон покрытия и следа линии визирования; отображение конструкции КА с учетом засветки ее элементов Солнцем; организация визуального отображения пространственного движения КА. Для решения этих задач используется программ-

ная система SIRIUS-S [9] и ее подсистема визуализации расчетных результатов в трёхмерной графике, созданная в среде программирования Delphi 7 с применением графической библиотеки OpenGL. Приводятся результаты практического применения разработанных алгоритмов аналитического представления законов наведения при анимации пространственного движения спутника землеобзора.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается спутник землеобзора, оснащенный телескопом с матрицами ОЭП в его фокальной плоскости. При съемке заданных участков поверхности Земли совокупностью маршрутов их сканирования матрицы ОЭП работают в режиме временной задержки и накопления (ВЗН).

Используются стандартные системы координат (СК) – инерциальная (ИСК) с началом в центре Земли, гринвичская геодезическая (ГСК), горизонтная (ГорСК) с эллипсоидальными геодезическими координатами L , B и H , орбитальная (ОСК) и связанная с КА (ССК) системы координат с началом в его центре масс O . Вводятся телескопная СК (ТСК, базис S ) с началом в центре оптического проектирования S , СК поля изображения O _ixⁱ yⁱzⁱ (ПСК, базис F ) с началом в центре O _i фокальной плоскости телескопа и визирная СК (ВСК, базис V ) с началом в центре O_v матрицы ОЭП. На поверхности Земли маршрут съемки отображается следом проекций ОЭП. Маршруту съемки соответствует закон углового наведения КА в функции времени, при котором происходит требуемое движение получаемого оптического изображения на поверхности ОЭП. При известном орбитальном движении центра масс КА рассматриваются задачи:

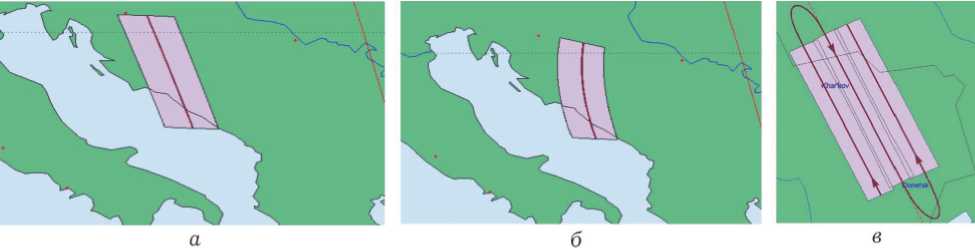
Рис. 1. Маршруты трассовой ( а ), с выравниванием СДИ ( б ) и площадной ( в ) съемки

• 1.    анализа поля СДИ на матрицах ОЭП с ВЗН для трассовых, ортодромических (геодезических) и криволинейных маршрутов с выравниванием продольной СДИ;

• 2.    аналитического представления законов углового наведения спутника;

• 3.    применения векторного полиномиального представления законов наведения при анимации пространственного движения спутника землеобзора.

АНАЛИЗ СДИ И СИНТЕЗ ЗАКОНОВ НАВЕДЕНИЯ

Задача вычисления кватерниона Л , векторов угловой скорости ю и ускорения £ решается на

основе векторного сложения всех элементарных движений телескопа (ТСК) в ГСК с тщательным учетом как орбитального, так и углового по-

ложения спутника, геодезических координат наблюдаемых наземных объектов, вращения Земли и множества других факторов. Пусть векторы-столбцы ю ^ и v е представляют в ТСК

текущей ориентации телескопа выполняется с помощью численного интегрирования известного нелинейного кватернионного кинематического уравнения с одновременным строгом согласовании с вектором угловой скорости. Созданные методы конкретизированы для трассовых (рис. 1 а ), протяженных криволинейных маршрутов с выравниванием продольной СДИ, рис. 1 б , для площадного землеобзора с последовательностью ортодромических маршрутов, рис. 1 в , а также для получения стереоизображений выбранных наземных объектов. Отметим, что осевые линии ортодромических маршрутов соответствуют геодезическим линиям заданной высоты H над земным эллипсоидом, т.е. здесь сканирование выполняется по дуге «большого геодезического круга» между точками маршрута с заданными геодезическими координатами L , B , H и заданным временем начала выполнения маршрута сканирования.

АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ

угловую скорость и скорость движения центра масс КА относительно ГСК, матрица C = || ^у || определяет ориентацию ТСК относительно ГСК, а скалярная функция D ( t ) представляет дальность наблюдения. Тогда для любой точки в фокальной

zl zl l l плоскости телескопа продольная Vy = Vy (у ,z )

У:

У:

и поперечная V Zi = V Zi (у¹ ,z^l ) компоненты вектора нормированной СДИ вычисляются по соот-

ношению [8,10]

i

y

. V

^yl 1

у¹ о

о

i ^ с .-^ i с -^, i S q Vel - У Юе3 + z юе2

уe         e yl e q Ve2 -   Юе3 - Z Юе1

q ^V e3 +  Ю 2 + У Ю 1

. (1)

Здесь у = у / f e и Z = z / J_e являются нормированными фокальными координатами указанной точки, где f_e – эквивалентное фокусное расстояние телескопа, скалярная функция q = l - ( с ₂ у + с ₃ z ) / с 1 и компоненты вектора нормированной скорости поступательного движения ^y e i = v ^e i ( t )/ D ( t ) i = 1,2,3 . На основе (1) получаются компоненты вектора-столбца ю е для всех типов сканирующей съемки, при этом расчет

Аналитическое представление законов наведения спутника при сканирующей съемке с заданной точностью основывается на полиномиальной интерполяции векторной функции модифицированных параметров Родрига о = e tg( 0 / 4) с традиционными обозначениями орта e Эйлера и угла 6 собственного поворота. Векторная функция ст взаимно-однозначно связана с кватернионом Л = ( X ₀ , Х ), X = { X ii }, l' = 1 ^ 3 явными прямыми ( Л ^ ст ) и обратными ( ст ^ Л ) соотношениями

ст = X/ (1 + X ₀ );

²        (2)

Х = 2 ст /(1 + ст ² ),   X ₀ = -^2 .

1 + ст

Прямые и обратные кинематические уравнения для вектора ст имеют вид

= 4 (1 -ст ²) ю + 2 ст х ю + ¹ ст^ст , ю ^;

4                                          (3)

ю = (1 _{+ ст} 2 ) 2 [(1 - ст ² )< ст - 2( ст X ст ) + 2 ст(<ст , ст} ].

Рассмотрим временной интервал T = [0, T ] , где выполняется сканирующая съемка, и введем обозначения для четырех точек этого интервала:

tk e T , t1 = 0, t2 = T / 3 , t3 = 2T / 3 и t4 = T . Пусть с помощью численного интегрирования кватернионного кинематического уравнения выполнен расчет маршрутного движения Л = Л(t), to = to (t), t e T, на концах интервала T вычислены значения кватерниона Л1 = Л(0), Л 4 = Л (T), вектора угловой скорости to1 = to (0) , to4 = to (T), вектора углового ускорения 81 = to (0), 84 = to (T), вектора модифицированных параметров Родрига (далее просто вектора Родрига) О1 = ст(0), ст2 = ст(12), ст3 = ст(13), ст4 = ст(T) и его производных стp = |(i -(стp)2)top+ 2стpxtop + 2стp(стp,top);(4)

-1

^ст p   2

-(ст ,ст )p, p p              p p p p

+ a xe +a a .co p p p p , p

+ a a +a (a p p, p p p, p /

, (5)

где значения индекса p = 1 и p = 4 соот- ветствуют граничным точкам интервала T. Интерполяция вектора Родрига ст(t) Vt e T выполняется векторным сплайном седьмого по-

рядка ст a (t) = "У astt с 8 векторами-столбцами as e R3, s = 0 ^ 7 неизвестных коэффициентов. Производные векторной функции ст a (t) пред- ставляются очевидными соотношениями ст a(t) = Е7 s аsts-1;

^ст a ⁽ t ) = E ⁷ s ⁽ s — ^ a S t s - ² .

Восемь векторов a _s коэффициентов сплайна ст a ( t ) однозначно определяются на основе:

• 1)    трех краевых условий ст a (0) = ст 1 ; a (0) =ст 1; ст a (0) =ст1 ^на левом конце интервала T , что дает

^а 0 = ^ст 1 , ^а 1 = ^ст 1 ^и а ₂ = ст 1 /2 ;      ⁽⁷⁾

• 2)    двух условий ^ст a ⁽ t 2 ) = ^ст 2 ; ^ст a ⁽ t 3 ) = ^ст 3 в двух внутренних точках t ₂ и t ₃ интервала T ,

  которые представляется соотношениями а ₃ + а ₄ 1 ₂ + а ₅ 1 ₂ ² + а ₆ 1 ³ + а ₇ 1 4 = b ₃;

а3 + а 413 + а5132 + а 6133 + а 7134 = b 4, где b 3 = ст 2 — (а 0 + а112 + а 212 ) /12, b4 — ст3   (а0 + а1 t3 + а2t3 )/ t3 ;

• 3)    трех краевых условий ст a ( T ) = ст ₄; ст a ( T ) = ст ₄; ст a ( T ) = ст ₄ на правом конце интервала T , что приводит к соотношениям а ₃ + а ₄ 1 ₄ + а ₅ 1 ₄ ² + а ₆ 1 ₄ ³ + а ₇ 1₄ = b ₅;

3 а ₃ + 4 а ₄ 1 ₄ + 5 а ₅ 1 ₄ ² + 6 а ₆ 1 4 + 7 а ₇ 1 ₄ ⁴ = b ₆;       (9)

6а3 + 12а414 + 20а 5142 + 30а614 + 42а714 = b7, где b5 =ст4 — (а0 + а114 + а214)/13, b6 =<г4 — (а1 + 2а214)/142, b =ст4 — 2а2 /t4.

Для определения пяти векторов a _s , s = 3 ^ 7 на основе (7) - (9) формируется соотношение AC = B , где строчные матрицы A = ^{[ а} 3 , ^а 4 , ^а 5 , ^а 6 , ^а 7 ^] ; B = [ b 3 , b 4 , b 5 , b 6 , b 7 ] ; C = [ c ₃, c ₄, c ₅, c ₆, c ₇] составлены из столбцов ^а s , ^b s , ^c 3 = t 2 ; ^c 4 = t 3 ; ^c 5 = t 4 ; ^c 6 = ^D 6 t 4 и c 7 = D 7 t 4 при t p = {1, t p , t p , t p , t 4 ^} p = ^2,3,4 и матрицах   D 6 = diag{3,4,5,6,7} ,

D ₇ = dlag{6, 12, 20, 30, 42} . Вычисление сразу всех пяти искомых столбцов а _s , s = 3 ^ 7 выполняется по явному матричному соотношению ^{[ а} 3 , ^а 4 , ^а 5 , ^а 6 , ^а 7^] = ^{BC 1} .