Векторные лазерные пучки Ханкеля с орбитальным угловым моментом

Лазерные пучки с орбитальным угловым моментом (ОУМ) интенсивно изучаются в оптике. Они применяются для беспроводной связи с увеличенной плотностью канала передачи информации [1], для оптического захвата и вращения микрочастиц [2]. Такие пучки имеют «иммунитет» к турбулентности, и их можно применять для зондирования атмосферы [3]. В задачах микроманипуляции важно, чтобы фокальное пятно не имело боковых лепестков [4]. Такому требованию удовлетворяют, например, недавно открытые лазерные пучки Ханке-ля [5]. Это непараксиальные скалярные вихревые лазерные пучки, которые, аналогично обычным Гауссовым пучкам, не имеют боковых лепестков. Также в задачах микроманипуляции требуется обеспечить острую фокусировку лазерного пучка. При острой фокусировке света, когда лучи сходятся в фокус под большими углами, в формировании фокуса существенную роль начинает играть поляризация. Для адекватного описания ОУМ в области фокуса требуется рассматривать все шесть проекций векторов напряжённости электромагнитного поля. В оптике известно небольшое число векторных световых полей, которые можно описать аналитически явным образом. Замкнутые аналитические выражения для ОУМ до сих пор получены только для параксиальных пучков Лагерра–Гаусса [6] и для векторных пучков Бесселя [7]. В [8] получены выражения для проекций векторов напряжённости электрического (Е-вектор) и магнитного (Н-вектор) полей электромагнитной волны. Все проекции E- и Н-векторов выражены через три интеграла, представляющих собой разложения по угловому спектру плоских волн. На основе проекций электромагнитного поля получены выражения для вектора Пойнтинга и ОУМ.

В данной работе рассмотрены новые векторные непараксиальные вихревые пучки Ханкеля. Для векторного пучка Ханкеля с линейной поляризацией получены явные аналитические выражения для всех проекций Е- и Н-векторов напряжённости электромагнитной волны. На основе полученных формул можно в аналитическом виде получить выражение для вектора плотности орбитального момента векторных пучков Ханкеля.

Векторные пучки Ханкеля и плотность углового момента

В [8] показано, что вектор углового момента (ОМ), равный j = £ц[г XS],                                          (1)

где £ - диэлектрическая проницаемость среды, ц -магнитная проницаемость среды, S – вектор Умова– Пойнтинга

S = 2 ( [ e X H * ] + [ e * X H ] ) ,                    (2)

где E и Н – вектора напряжённости электрического и магнитного поля электромагнитной волны, может быть рассчитан для волны с линейной поляризацией, направленной вдоль оси x , с помощью следующих выражений для всех проекций векторов напряжённости поля:

Ex = I , x

E y = 0,

E z =

1 д 1 ₂

k д x ’

H =

i д ² 1 ₂ ц к ² д y д x

Hy = 4 + y ц

i д ² 1 ₂ Ц кг "x? ,

H z =

i д 1 1 ц к д y

В (3) используются следующие интегралы:

^ 2n

I1_ jj A (p, 6)x

x exp [ zkr p cos ( ф - 6 ) - kz4 p ² - 1 ] p d p d 6 ,

1 2 "j I A ^H x

00 Vp - 1

x exp [ zkr p cos ( ф - 6 ) - kz4 p ² - 1 ] p d p d 6 ,

^ 2n

13 _ jj a (p, 6) Vp2-1 x xexp[zkrpcos(ф - 6) - kz4p2 -1 ] pdpd6,

где A (ρ, θ) – комплексная амплитуда спектра плоских волн, ( x , y , z ) – декартовы координаты, z – координата вдоль оптической оси, ( r , φ, z ) – цилиндрические координаты и (ρ, θ) – безразмерные полярные координаты спектра плоских волн (то есть ρ – это отношение проекции волнового вектора k на поперечную плоскость к волновому числу k ).

Двойные интегралы (4) – (6) сводятся к одинарным интегралам, если можно явно выделить «вихревую» составляющую амплитуды спектра плоских волн:

A ( p , 6 ) _ A ( p ) exp ( zn 6 ) ,

где n – целое число. С учётом (7) выражения (4)–(6) будут иметь вид:

1 1 _ 2 n z V ^ф x ^

x j A ( p ) exp ( - kz4 p ² - 1 ) J n ( kr p ) p d p , 0

1 ₂ _ 2 n z n e n ^ф x

4 Ж exp ( ^{- kz} V p ^{2 - 1} ) J n ( kr p ) p d p , о Vp²-i     ^{v 7}

13 _ 2nz'ne'nфx xj A(p)4p2-1 exp(-kz4p2 -1) Jn (krp)pdp, 0

где J n ( x ) – функция Бесселя первого рода n -го порядка. Заметим, что выражения (8) – (10) связаны между собой с помощью производных:

1 d 1 1 _ 1 d ² 1 ₂

I ^{3 _}" k d z ⁼ k? "z?

,

I _- 1 d l l

¹ k d z

.

Пусть A ( p ) = p ⁿ . При этом основной вклад в поле дают неоднородные затухающие волны. Мощность такого спектра плоских волн неограниченная, и мощность светового поля, имеющего такой спектр, тоже не ограничена. Если спектр плоских волн задаётся такой степенной функцией, интегралы (8)–(10) можно вычислить с помощью функций Ханкеля:

I _ 2nz'ⁿe^{in ф} j p ⁿ exp( - kz4 p ² - 1) J„ ( kr p ) p d p _

0                                          (12)

_ z ⁿ "W ² zr ⁿe^{in Ф} V _{n + 3/2} ( R ) ,

12 _ 2nznen фx xj p— exp (-kz 4 p2-1) Jn (kr p)p dp _

0 Vp² -1     ^v

_ z ⁿ n.' ^; r ⁿe^{in Ф} V _{n + 1/2} ( R ) ,

13 _ 2nznenфx xjpn4p2-1 exp(-kz4p2 -1)Jn (krp)pdp _

_ z ⁿ nx re ^ф [ z V n +5/2 ( R ) - k "V n +3/2 ( R ) ] ,

V n+v( R ) =

H n +V ( kR )

R n +V        ,

R _ V r ² + z ² ,

dv n +v ( R ) _

dx dV n+v( R) _

^d y

■^V n +V+1 ( ^R )( kr cos ^ф) ,

■^V n +V+1 ( ^R )( kr sin ^ф) ,

где H V2) ( x ) _ J _v ( x ) - z Y ( x ) — функция Ханкеля, Y^x ) -функция Неймана.

Из (12)–(14) видно, что интегралы I 1 , I 2 , I 3 равны соответственно пучкам Ханкеля 2-го, 1-го и 3-го типов [5]. Вспомогательные уравнения (16) используются для получения последующих формул.

С помощью (3) и (12)–(15) найдём все проекции векторного светового поля Ханкеля с линейной поляризацией ( E_y ( r , ф , z ) = 0):

E _x ( r , ф , z ) _ z n ^{+ 1} nX ^1/2 zr n e' n V n +3/ ₂ ( R ) ,

Ez (r, ф,z)_

z n ^{+ 1} X ^3/2 r ^{n - 1} e 'n ^ф

-----------x

x[ ne -* V n +1/2 ( R ) - kr² cos фТ n +3/2 ( R ) ] ,

„ ,            zⁿ X ⁵ / ²r ^{n - 2} e ^{zn ф}

H (r,ф,z)_----;-------x

4лц x [ in (n -1) e-z 2фТ n+1/2 (R )-

- znkr ² e ^{- z Ф} Т n +3/2 ( R ) +

+ k2r4 sin ф cos фТn+5/2 (R)] , zn X5/2 rn-2 em ф

H (r, ф, z) _------------x y            4лц x [ n(n -1)e-z 2фТ n+1/2 (R )-

- 2 kr ²(1 + ne ^{- z ф} cos ф ) V _{n + 3/2} ( R ) +

+ k ² r ² ( z ² + r ² cos² ф ) Т n +5/2 ( R ) ] ,

_A .   z ⁿ X ^3/2 zr ^{n - 1} e ^{m ф}

H z ^{( r} , ^ф , ^{z )_}----- 2^----- ^x

x[ zne -V n +3/2 ( R ) - kr ² sin фV n +5/2 ( R ) ] .

Из (1) проекция на ось z ОУМ будет иметь вид:

j z _^ 2 [ x Re ( EH - H z E x ) + y Re ( E z H y ) ] . (22)

Из (22) видно, что выражения (17)–(21) позволяют в замкнутой форме (хотя и громоздкой) получить плотность проекции ОУМ на оптическую ось для непараксиального векторного пучка Ханкеля.

Из (17) видно, что поперечная проекция Е-поля имеет радиально-симметричное распределение интенсивности с нулевым значением интенсивности на оптической оси (при r =0), кроме начальной плоскости ( z =0) и кроме n =0, когда пучок Ханкеля совпадает со сферической волной. Из (18) видно, что продольная проекция Е-поля не будет обладать радиальной симметрией, а будет обладать симметрией относительно обеих декартовых координат и вытянута вдоль направления поляризации (вдоль оси x ). Также продольная проекция Е-поля на оси будет всегда равна нулю, кроме случая n = 1. При n = 1 в центре распределения интенсивности находится седловая точка: минимум по координате x и максимум по координате y . Значит, и полная интенсивность векторного пучка Ханкеля с линейной поляризацией I = | E x |² + | E z |² не будет обладать радиальной симметрией относительно оптической оси.

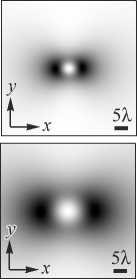
На рис. 1 показаны распределения поперечной и продольной составляющих интенсивности, а также суммарной интенсивности (т.е. величины I_x = | E_x |², I_z = | E_z |², I = I_x + I_y соответственно) векторного пучка Ханкеля с линейной поляризацией вдоль оси x , с топологическим зарядом n = 1 в плоскостях z =5 λ и z = 10 λ .

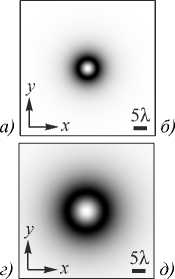
Рис. 1. Интенсивность (негатив) поперечной (а, г), продольной (б, д) и суммарной (в, е) интенсивности векторного пучка Ханкеля (длина волны λ = 532 нм, топологический заряд n = 1) в плоскостях z = 5 λ (а, б, в) и z = 10 λ (г, д, е)

Заключение

Комплексные амплитуды скалярных пучков Ханке-ля, полученных в [5], использованы для получения векторных пучков Ханкеля. Получены в явном виде амплитуды всех проекций векторов напряжённости электрического и магнитного полей (17)–(21) для векторного непараксиального вихревого пучка Ханкеля с линейной поляризацией. Тем самым получены в замкнутой аналитической форме выражения для проекций вектора Умо-ва–Пойнтинга (УП) (2) и ОУМ (1). До сих пор только для непараксиального векторного пучка Бесселя [7] и параксиальных пучков Лагерра–Гаусса [6] можно было записать аналитически проекции этих векторов УП и

ОУМ. Хотя интенсивность поперечной электрической компоненты E_x (17) обладает радиальной симметрией, интенсивность других проекций светового поля E z (18), H x (19), H y (20) и H z (21) не имеет радиальной симметрии для линейно-поляризованного пучка Ханкеля.

Работа выполнена при поддержке Министерства образования и науки РФ, гранта Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9), а также грантов РФФИ 13-07-97008, 14-29-07133 и 1407-31092, 15-07-01174.