Верхняя оценка силовых и деформационных параметров равноканального углового прессования в параллельных каналах

Рис. 1. Схема углового прессования в параллельных каналах: а - ширина канала; S - смещение каналов; 2 9 - угол пересечения каналов

Согласно схеме, изображенной на рис. 2, один из очагов деформации, расположенный вблизи линии пересечения каналов матрицы, представляется в виде жестких блоков 1, 2, 3, 4, скользящих относительно друг друга и по границам с жесткой зоной 5. Вдоль границ блоков (треугольных по В. Джонсону) компоненты скоростей перемещений претерпевают разрывы. Внутри каждого блока поле скоростей перемещений однородно с одинаковым вектором скорости для всех точек блока. На этом основании определяют поле скоростей, которое при правильном построении всегда является кинематически возможным. Число и размеры блоков выбирают произвольно. Вдоль границ блоков касательные напряжения максимальны тк=к, на свободных поверхностях τk=0, а на контактных

подчиняется закону Зибеля [6]

Т = 2 mk =

2 mc_s

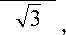
где m – фактор трения (0≤ m ≤0,5).

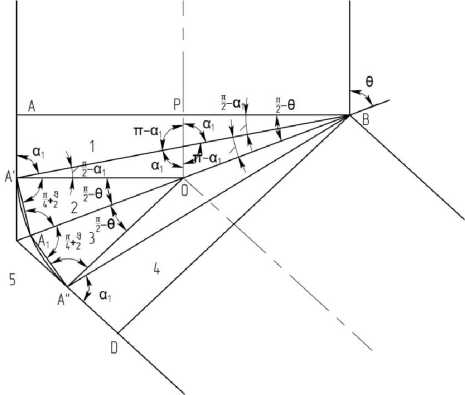
Рис. 2. Схема разбиения очага деформации на жесткие блоки

Для установления влияния радиуса сопряжения каналов на силовые параметры введем его величину

R=a/n; (1≤n≤a) (6)

Следует отметить, что попытки учета радиуса сопряжения каналов предпринимались. Работы [8, 9] посвящены компьютерному моделированию силовых и температурных параметров. В большинстве случаев теоретического анализа радиус назначался либо равным ширине канала [3, 10], либо половине ширины [11]. Из геометрических параметров найдем длины границ блоков. Построив годограф скоростей (рис. 3), определим скорости относительных перемещений жестких блоков через известную скорость деформирования v 1 и угол пересечения каналов 2 θ . Кроме того, определим нормальные составляющие скоростей перемещений vⁿ ij . Результаты сведены в табл. 1.

Согласно (2) и (3) запишем уравнение баланса мощностей внутренних и внешних сил с учетом сил трения [12].

Pav 1 = k ( 1 12 v ₁₂ + 1 23 v 23 + 1 34 v 34 + 1 ₂₅ v 25 + 1 35 v 35 ) + 4 mkA ' A • v 1

Поскольку блоки жесткие, мгновенная мощность внутренних сил, включая контактное трение, выражается уравнением [7]:

Проведем необходимые преобразования:

Pav

2 k

,        1                         a ( n - 1)

l 12 v 12 ⁺ - ¹ 23 v 23 ^{+ 1} 25 v 25 ^{+ 2} m---ctg ⁹ ' v 1

2 n

____      •

W = ^ T_kU j l j b j

В окончательном виде получим удельную силу

прессования:

где u - скорость относительного скольжения i и j блоков; l ij – длина границы i и j блоков при плоской деформации; b ij – длина проекции площадки контакта в направлении оси y.

Активная мощность, развиваемая деформирующей силой P:

ntg 9   .        ntg 9

cos arctg----+ sin arctg-- n -1            n -1

p

2 k

2 n - 1

n

( n - 1) 2 n ² sin² 9

•

k

•

k k

1 - -___2___— tgff - arctg ntg^) +1

k ^{2         n - 1} J )  )

+

•

W A = Pu 0

,

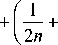
2sin 9

(n  9

cos —I— \ 4  2

1 k .         ntg 9

• sin arctg        •

2 n sin 9 )           n - 1

где ’ - скорость деформирования.

u 0

Из равенства мощностей внутренних (2) и внешних (3) сил находим необходимую для прессования силу:

ntg9 k - arctg n -1)

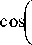
n 9 1 22

, V 2                      ntg 9

+ a/1 + sin 9 • sin arctg n                      n - 1

(n  9        ntg 9 k

• cos — +--- arctg      I +

\ 4  2        n - 1 )

• р= T/Uy lb

n - 1

+ 2 m---ctg 9

n

• u0

.

Для случая плоской деформации, обозначив ширину канала матрицы через a , можно выразить удельную силу:

P =

•

^ки«1у

Варьируя параметрами, входящими в зависимость (8), такими, как n , влияющий на значение радиуса споряжения каналов, m- фактор трения, и θ – половина угла пересечения каналов, были получены результаты, представленные на рис. 4.

• u0 a

.

Таблица 1. Параметры линий разрыва и скоростей перемещений

Гра ницы H	l ij	v ij			n vij
1-2	a   • V(2 n - 1)sin 2 0 + ( n - 1) 2 n sin 0	v 1	ntg 0   .         ntg 0 ) cos arctg --+ sin arctg n - 1            n - 1 f 0         ntg 0 )  _ tg--arctg ----- -1 s V 2       5 n - 1 J • f 0         ntg 0 )  . tg \ - - arctg ----7 | + 1 V   V 2          n - 1 J            J		v 1 sin	f n      Z>) 1 arctg \---- -tg 0 _     V n -1    J
1-5	a ( n - 1)      „ actg a =-- ctg 0 n	v 1			0
2-3	a (sin 0 + n - 1) n sin 0	.        ntg 0 v 1 sin arctg n - 1 f n  0        ntg 0 ) • cos \ —1--- arctg -----| • V 4   2         n - 1 J 1 f П 0 ) cos \ —1I V 4   2 J			v 1 sin • sin \ f • cos V	f n       i arctg \----- T tg 0 | • _     V n - 1     JJ П 0 i +     • 4   2 J П 0            л — + — 42 f n    „) - arctg \ — -g^9 1 _V n - 1     JJj
2-5	a • V2 • V1 + sin 0 n	.        f ntg O ) v 1 sin arctg \------| • V n - 1 J f n  9        ntg 0 ) • cos \ —1--- arctg -----| \ 4  2        n - 1 J			0
3-4	“    • V(2 n - 1)sin2 0 + ( n - 1)2 n sin 0	v 1	'           ntg 0    .         ntg 0 cos arctg --+ sin arctg-- n - 1            n - 1 f 0        ntg 0 ) tg\ - - arctg ----7 | - 1 V 2         n - 1 J • f 0         ntg 0 ) tg \ - - arctg ----7 | + 1 V   V 2          n - 1 J             j		0
3-5	a • V2 • V1 + sin 0 n	.        f ntg 0 ) v 1 sin arctg \------| • V n - 1 J f n  0        ntg 0 ) • cos \ —1--- arctg -----| \ 4  2        n - 1 J			0
4-5	a ( n - 1)      „ actg a =-- ctg 0 n	v 1			v 1 sin	f n     n) arctg 1 —- tg 0 1 L     V n -1     Jj

При ширине канала матрицы а=10 мм, одинаковом радиусе сопряжения каналов (R=2) увеличение фактора трения приводит к росту относительной силы прессования p/2k; при одинаковом факторе трения (m=0,15) увеличение радиуса сопряжения каналов способствует уменьшению удельной силы. Оценим деформированное состояние металла заготовки. Суммарная деформация сдвига складывается из сдвиговых деформаций на линиях разрыва скоростей:

Y 12 =

n - 1 + ntg 0

f 0         ntg 0 )

g - ^- arctg —- |

V 2         n - 1 J

f 0        ntg 0

tg l -- arctg —7

V 2         n - 1

- 1

^Y 23 =

+ 1

;

0 cos

Итак, суммарная деформация сдвига с учетом

двух очагов деформации:

Y = 2

Y = Y 12 + Y 23 + Y 34 • ;

Y ij

ij

v

n ij

n - ¹ + 1 ntg 0

f 0        ntg0) , tg\ ~-arctg----7 | +1

V 2         n - 1 J

⁺    0

cos

Интенсивность пластических деформаций найдем из соотношения:

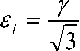
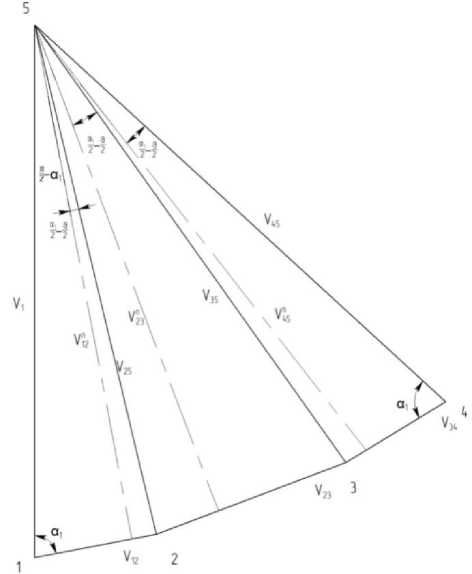
Рис. 3. Годограф скоростей

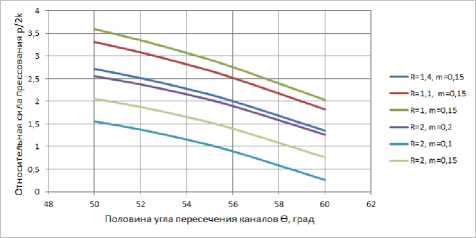
Рис. 4. Изменение относительной силы прессования от основных технологических параметров

Рис. 5 иллюстрирует изменение суммарной сдвиговой деформации (а) и интенсивности накопленной деформации (б) за цикл обработки. Из графика видно, что с увеличением радиуса сопряжения каналов матрицы, суммарные сдвиговые деформации уменьшаются. Это объясняется изменением характера деформации в сторону изгиба заготовки при увеличенных радиусах сопряжения. Обратная картина наблюдается в изменении интенсивности накопленных деформаций, здесь при увеличении радиуса сопряжения каналов этот показатель деформированного состояния уменьшается.

Выводы: установлена взаимосвязь и теоретически обоснована зависимость между значениями таких геометрических параметров, как радиус сопряжения и угол пересечения каналов матрицы, и энергосиловыми параметрами технологического процесса равноканального углового прессования, также выявлено влияние перечисленных параметров на характеристики деформированного состояния прессуемой заготовки.

Рис. 5. Изменение суммарной сдвиговой деформации (а) и интенсивности накопленной деформации (б) за цикл прессования