Verification of Kolmogorov equation usability for reproduction and death processes

Simulation of queuing systems (QS) is an effective tool for researching of production systems. Many foreign [1, 2] and Russian [3, 4] sources show the effectiveness of use of simulation in a study and optimization of activities of enterprises and their subdivisions. In particular, it is shown that queuing and multi-agent modeling is an effective in a decision support systems of a production management [5]. Let’s notice that the multi-agent system (MAS) is a simulation model in which objects (“agents”) are characterized by some autonomy, decentralization and limited ideas [6]. Extremely autonomy and limitations are characteristic of channels and transacts of QS. Software agents of MAS are described by algorithms of their own actions and interactions with other software agents.

Statistical distribution of random variables has a great influence on the modeling results. As shown in [7] a model of joint works of titanium plant subdivisions gives very different results in case of uniform or Poisson distributions (Fig. 1).

The specific units of reaction and factors do not matter in this case. The non-linear relationship between the reactions with normal and Poisson distributions of the factor is important. This dependence is also characteristic of other queuing systems. The uniform distribution is “worst” in some manner. It provides biggest deviations of a result value of any QS. Meanwhile the uniform distribution is assumed by default exactly when no reliable information in an input data. The Gaussian distribution could be used customarily when it can be confirmed by statistical testing of the hypothesis.

Using of conclusions obtained solely through the use of simulation programs (QS) is considered insufficient in qualifying scientific jobs (thesis). Famous methodologist of dissertation research in Russia considers [8] that “…an idea and technique of simulation is so simple that you can learn it of some days in a matter. Therefore, use of them … cannot be a confirmation of the high qualification of a thesis”. The scientific tradition requires supplementing QS calculations with analytical research.

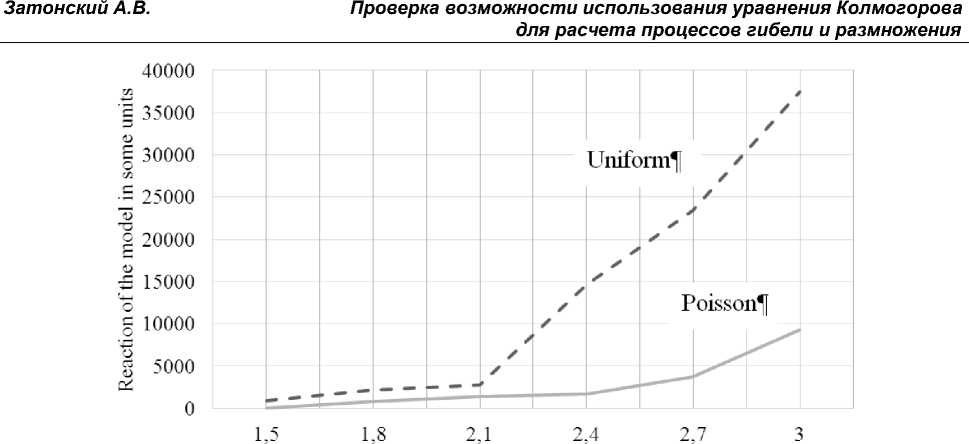
Value of main factor in some units

Fig. 1. Dependences between the factor and the reaction of the model with different statistical distributions of the random factor variable

Kolmogorov’s equation and many models generated by such approach are one of the most common mathematical tools for the research of QS. A main idea of the method is in follow. A velocity of Markov processes state changing is determined by probabilities of neighboring states and the flows of their changes:

' dp^ ¹ - ^ X j P j ( t ) .

< dt      j * i z pi (t)-1.

where p i ( t ) . P j ( t ) - probabilities of i -th and j -th states of QS in time t. X j - change state flow from i -th state to j -th ( X j >  0) or vice versa ( X j <  0). Thus. it is possible to calculate the limit probabilities of dp, ( t )

the state of the system when---— - 0 V i .

dt

However, it is obvious that the Kolmogorov’s equations are not valid for all statistical distributions. Let consider the simplest model of “death and reproduction” as one-channel QS with a limited queue. If a loading flow X is smaller of an unloading flow ц . we can get a solution of the Kolmogorov equa-

X . _ tions as the probability of an empty queue p0 -1 -p [9]. where p - — < 1. That means the queue will Ц not be empty at any time. At the same time, if zero dispersion of the loading and unloading flows is observed, queue will be empty forever. You can easily imagine it if transacts arrives exactly via 1 time units and being processed in a channel exactly — t.u.. where — < —. So if we calc a production system ц ц X as QS by the Kolmogorov’s equations we can obtain a wrong result if some factors has uniform distributions. That is why a question about validity of the Kolmogorov’s equations is ambiguous and practically important in relation to the statistical distributions of the intensity of loading flows and their processing. The problem of studying of the usability limits of the Kolmogorov’s equations and similar mathematical models is usually not considered in scientific sources (for example [10, 11]) despite the obvious need to solve it.

We attempt to experimentally “verify” the Kolmogorov’s equations using some common different simulation environments in this article. We will make a theoretical calculation of the limiting state probabilities of QS “death and reproduction” and their comparison with the results experimentally obtained

Инфокоммуникационные технологии и системы by GPSS World and AnyLogic programs. As examples two schemes is considered: a multichannel system with failures (the so-called Erlang problem), and a single-channel system with a limited queue.

Multichannel QS with failures

Let us consider a system includes three channels to process of transacts. Let a medium loading flow intensity is equal λ = 0,005 s^–1, and processing (unloading) flow intensity is equal μ = 0,0025 s^–1. The system has four states: S 0 – all channels are free, S 1 – one channel is free but others are busy and so on until S 3 . Let p 0 . . p ₃ are probabilities of the states S 0 _ S 3 respectively, p ₀ ( t ) = 1, p i ( t ) = 0 V i = 1,3. A state graph of the system is presented on Fig. 2.

λ         λ         λ

μ         2μ 3μ

Fig. 2. A state graph of three-channel QS with a queue

The flow of transacts leads the system from any left state to the next right one with the same intensity λ sequentially. An unload intensity leads the system from left to the next right state. The last depends on state of the sysnem (from a number of busy channels). For example, the system can turn from state S 2 to S 1 if any of channels (1 or 2) will terminate the processing. That is why a summary unload flow is equal 2μ.

So, the system of Kolmogorov’s equations is a follow in a limit stationary mode:

'^X- p о = ц^-A,

< X- p i = 2 -ц- p 2 ,

X-p 2 = 3-Ц-p з,.

. p 0 + p i + p 2 + p 3 = ^1.

Probabilities p ₀ ... p ₃ is equal consequently:

(   1   727

p 0 = 1 ■     ',,' -       = 0.1579, p 1       p = 0.3158,

(   ц 2!ц2 3!ц J p2 = X1A -^ = 0.3158,       p3 = X-p  Xp0 = 0.2105.

2 - ц 2 - ц ²                                 3 - ц 6 - ц ³

Single-channel QS with a queue

Let us consider a single-channel QS with a three cells queue and the same flow rates. The system has 5 possible states: S 0 – the channel is free, a length of the queue is 0, S 1 – the channel is busy, the queue is free, S 2 – the channel is busy and the length of the queue is 1 and so on until S 4 – both the channel and the queue are full. Probabilities of the states are p ₀ ... p 4, beginning conditions are p 0 ( t ) = 1, p i ( t ) = 0 V i = 1,4. A state graph of such system is similar to Fig. 2 but an unload flow rate is μ at any state.

So, the system of Kolmogorov’s equations is a follow in a limit stationary mode:

p 0 = (1+ P + P2 + P3 + P4)-1 = 0.5161, p1 =p- p0 = 0.2581,

, p ₄ =p ⁴ - p ₀ = 0.03226, where р = Х/ц = 0.5.

Modeling program and results

We designed two programs to solve both tasks: one by GPSS (General Purpose Simulation System) language and second in AnyLogic modeling suite. We can create some distributions in GPSS using libraries or using tables with points of the distribution function [5]. We used different kinds of statistical distributions to determinate whether they could be coincided with result of Kolmogorov’s equations solving:

• •    Uniform;

• •    Normal;

• •    Gamma;

• •    Exponential;

• •    Weibull;

• •    Geometric.

Some of them are presented in GPSS/AnyLogic libraries, another are realized with table functions. All results and theoretical results above are in Table 1. Distributions marked “*” is the same but with modified parameters described below. A GPSS listing for multi-channel QS with failures is the follow: ; ===== main block ========= kan storage 3 ; 3 channels generate (Normal(1,200,0.01)) ; a kind of distribution gate snf kan,out enter kan advance (Normal(1,400,0.01)) leave kan terminate out terminate ;======= secondary flow to computation =========== generate 1   ; secondary flow savevalue 1,S$kan ; a current content of the storage test e x1,0,met1 ; if the channel is free, then +1, ; else go to met1 savevalue empty+,1 ; count if the channel is free terminate 1 ;------------------------------------------- .

met1 test e x1,1,met2

savevalue full1+,1 ; a channel 1 is busy terminate 1

;

met2 test e x1,2,met3

savevalue full2+,1 ; two channels are busy terminate 1

;

met3 test e x1,3

savevalue full3+,1 ; all channels are busy terminate 1

start 1000000

Table 1

Comparison of simulation results in GPSS with theoretical conclusions

Stochastic distribution	Multi-channel QS with failures				Single-channel QS with a queue
	p 0	p 1	p 2	p 3	p 0	p 1	p 2	p 3	p 4
Bu Kolmogorov’s equations	0.1579	0.3158	0.3158	0.2105	0.5161	0.2581	0.1290	0.06452	0.03226
Uniform	0.0244	0.2237	0.6047	0.1689	0.7252	0.2714	0.0003	0.0003	0.0003
Normal	0.0002	0.00029	0.999	0.000089	0.5008	0.4959	0.0004	0.0002	0.0002
Gamma	0.1587	0.3172	0.3148	0.2083	0.5072	0.2566	0.1342	0.0679	0.0316
Exponential	0.1587	0.3171	0.3148	0.2084	0.5072	0.2566	0.1342	0.0679	0.0316
Weibull	0.1587	0.3171	0.3148	0.2084	0.5072	0.2566	0.1342	0.0679	0.0316
Geometric	0.1527	0.3136	0.3234	0.2090	0.5165	0.2591	0.1275	0.0641	0.0303

Инфокоммуникационные технологии и системы

Numbers of states are stored in variables Empty and Full. They are counted by a special flow from a block “generate 1” when the model works. Probabilities are the numbers divided on their sum.

An analogue program is designed for the single-channel QS with a limited queue. All changes was only in a follow block: nak storage 3

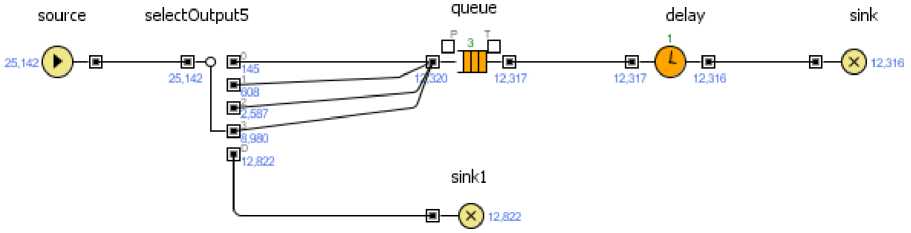
generate (Normal(1,200,0.01)) ; a kind of distribution gate snf nak,out ; if no space in ‘nak’, then ‘out’ enter nak seize kan leave nak advance (Normal(1,400,0.01))

release kan terminate out terminate Both models are realized in AnyLogic too [12]. For example the single-channel QS with a limited queue is shown on Fig. 3. Results of modeling with different distributions are shown in Table 2.

(5 capacity_queue

(3 entry interval

(3 time_work

(3 capacity_canal

О total_count	О	probability_success
25,142		0,49
О success	о	probability_fail
12,316		0.51
	о	p0 canal Free
О canal_free		0.006
145	о	pl_queue_free
Л canal_engaged_queue_free		0.024
608	0	p2_fulll
queue_fulll		0.103
2,587 О queue_full2	0	p3_Full2 0.357
8,980	0	p4_Full3
Q queue_full3		0.51

Fig. 3. The model and results of modeling with an exponential distribution for single-channel QS with a limited queue

Table 2

Comparison of simulation results in AnyLogic with theoretical conclusions

Stochastic distribution	Multi-channel QS with failures				Single-channel QS with a queue
	p 0	p 1	p 2	p 3	p 0	p 1	p 2	p 3	p 4
Bu Kolmogorov’s equations	0.1579	0.3158	0.3158	0.2105	0.5161	0.2581	0.1290	0.06452	0.03226
Uniform	0.007	0.523	0.44	0.03	0.501	0.499	3.9E-05	1.9E-05	1.9E-05
Normal	0.00002	0.5	0.5	0	0.5	0.5	0.00004	0.00002	0.00002
Gamma	0.156	0.315	0.317	0.211	0.516	0.259	0.13	0.064	0.031
Exponential	0.155	0.318	0.317	0.21	0.516	0.259	0.13	0.064	0.031
Weibull	0.155	0.318	0.317	0.21	0.516	0.259	0.13	0.064	0.031
Geometric	0.156	0.318	0.316	0.21	0.514	0.257	0.132	0.065	0.032
Erlang	0.155	0.318	0.317	0.21	0.516	0.259	0.13	0.064	0.031

A medium errors between results obtained with GPSS and AnyLogic with different distributions is in Table 3.

Table 3

Medium errors of modeling in different tools in comparison witn Kolmogorov’s equations

Distribution	GPSS , %	AnyLogic , %
Uniform	63,2	75,8
Normal	101,1	79,3
Gamma	1,8	0,9
Exponential	1,8	1,0
Weibull	1,8	1,0
Geometric	1,7	0,8
Erlang	–	1,0

There are no significant differences between using inbuilt or table functions of distributions calculations, if the last set correctly. For example, a error for inbuilt exponential distribution is 1,8% as shown above, and for table function is 2,6%.

Results and conclusion

As a result Kolmogorov’s equation could be used for analytic QS modeling in tow cases:

• 1.    If a stochastic distribution is exponential.

• 2.    If other distributions are close to the one especially. For example, in built functions GAMMA(Stream, Locate, Scale, Shape), WEIBULL(Stream, Locate, Scale, Shape) etc. a parameter ‘Shape’ must be set to Shape = 1.

Otherwise results of modeling are very different from theoretical ones even in the simplest systems described here. They will be even more different in complex QS’. So far as uniform distribution is the default, results of production QS modeling cannot be compared with theoretical ones in any case. A scientist has to make sure in exponential kind of each stochastic parameter of QS before try to use common analytic modeling methods.